结合 MCP 和 RM 的检测质量评估方法

结合MCP和RM的检测质量评估方法

王维峰施江焕李蓓蓓

(宁波市计量测试研究院，宁波 315048)

摘要：在分析现有测量系统检测质量评价算法的基础上，针对各检测实验室测量系统对产品质量控制获取满意检测结果的预控能力不足，提出基于结合测量能力指数(MCP)和标准样品(RM)的过程质量特性分析与控制方法，采用MCP对小批量柔性检测质量进行评估。实例表明，该方法可以实现对各检测实验室在小批量检测条件下的产品质量控制，在各检测实验室测量系统检测结果趋同性方面优于传统的其它检测质量评价算法。

关键词：测量能力指数；测量系统；趋同性

作者简介：王维峰，男，1964年出生，高级工程师，研究方向为计量检测和质量控制，E-mail:wangweifeng9@163..com。

DOI:10.3936/j.issn.1001-232x.2015.01.017

收稿日期：2014-05-20

An evaluation method of detection quality based on MCP and RM.WangWeifeng,ShiJianghuan,LiBeibei(NingboInstituteofMeasurementandTestingTechnology,Ningbo315048,China)

Abstract:This paper proposed a new method of detection quality evaluation based on measuring capacity index(MCP)and standard samples(RM), which could use MCP to evaluate the small batch flexible detection quantity. Examples showed that the method could be used for product quality control of the laboratory in the small batch detection condition. The convergence of detection result was better than the raditional detection quality assessment algorithms.

Key words：Measuring capacity index; measurement system; convergence

随着市场对产品质量的监管越来越严格，检测技术和仪器设备作为监管产品质量的重要支撑和风险预警的重要手段，对含量的准确性评价成为产品质量控制的研究热点之一。传统的空白试验、平行样测试、加标回收试验、对有证标物的检测、人员比对、方法比对和实验室能力验证等作为考察检测实验室测量能力的重要技术手段，在检测领域得到广泛的使用。但此类方法仅关注检测结果，忽略了对测量系统的检测质量波动的评价，最终导致评价结果与实际值不太一致，影响评价结果的准确性。

ISO导则30：1992给出了标准样品(RM)定义为“具有一种或多种足够均匀的和很好确定了的特性值的材料或物质，可以用来校准仪器、评价测量方法和给材料赋值。”RM的特性量值可以用作实验室内部或实验室间比对的标准值。测量能力是指在检测过程处于稳定状态时，该过程的检测结果能满足质量要求的能力，其可用测量能力指数(MCP)来衡量[1，2]。MCP是指将测量能力量化后的评价标准，表示测量能力满足质量技术标准的能力。

检测质量的波动主要来源于测量系统[3]，测量系统是由人、机、料、法、环等构成的一套

系统，在检测质量稳定时，要求这5个因素都处于受控状态，并且有足够的统计样本容量，对异常波动提出预警和纠正措施，这对小批量柔性检测过程较为困难。本文提出一种基于MCP和RM的检测质量评估新方法，以测量重复性和检测过程均值偏移为研究对象，重点描述了用MCP控制小批量柔性检测质量评价算法。该算法通过测量数据集的实验结果证明，在各实验室测量系统检测结果趋同性方面优于传统的其它检测质量评价算法，有效地提高了测量系统评价的准确性。

1基于MCP的检测质量评估方法

由于检测过程中受内在或外在的随机因素和系统因素的影响，使测量系统检测过程的输出总是与检测目标值之间存在误差。基于美国朱兰博士提出的过程能力指数(PCI)，在测量均值μ与目标值T有偏移时，Hsiang和Taguchi解释了其质量损失原因为质量特性的波动σ和检测过程平均偏移ε，提出了更适合小批量柔性检测过程的平方型田口指数通用算式[4]。

(1)

式中：LSL，USL分别为上、下技术规格限；σ为标准差； (μ-T)2表示测量均值偏移目标值的附加惩罚。

测量能力指数的评价原则是检测过程既有充足的测量能力，同时检测过程又有合理的经济性，在一个适当的范围内取值。一般情况下，可根据表1对测量能力进行评价[5]。

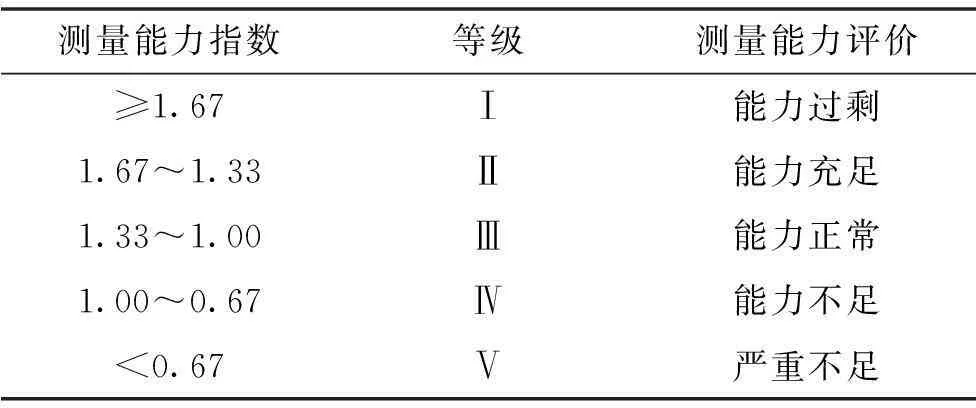
表1　测量能力指数的评价参考

2结合MCP和RM的检测质量评估方法

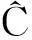
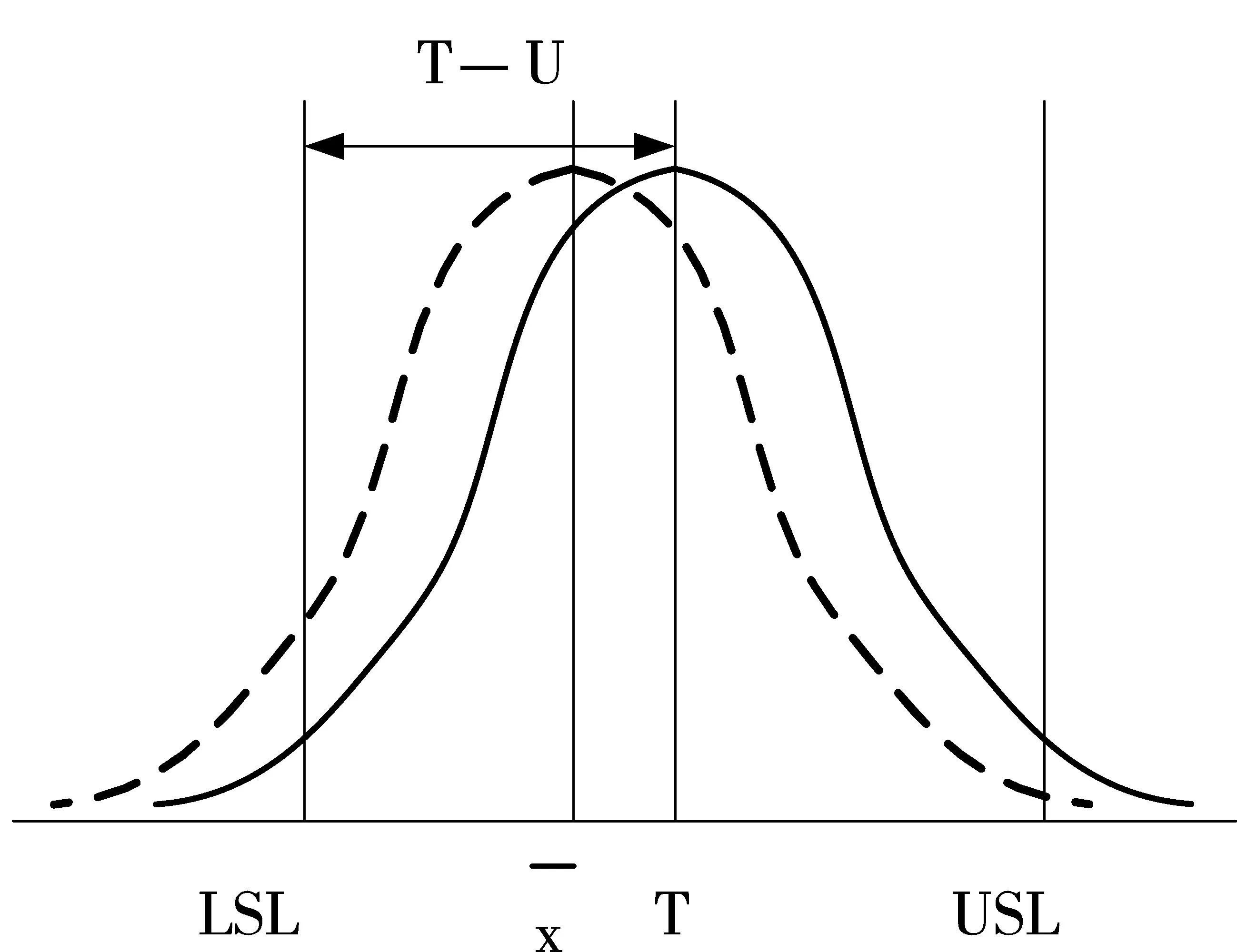
图1　有偏移时测量系统各参量示意图

(2)

3实验部分

3.1　方法

选用39.7%唑酮草酯可湿性粉剂为试样，用乙腈溶解后，以乙腈+水=60%+40%(体积分数)为流动相，使用C18不锈钢柱和紫外检测器，在波长245nm下，对试样中的唑酮草酯进行反相液相色谱分离和测定，利用标准样品(RM)峰面积外标曲线法定量。

3.2　试剂、溶液和设备

实验水(高纯水)；乙腈(色谱纯，德国Merck公司)；唑酮草酯标准品(纯度99.36%，Urel为2%，德国Dr. Ehrenstorfer公司)；Agilent1200高效液相色谱仪(HPLC)，配有紫外/二极管阵列检测器(美国Agilent公司)；电子天平(分辨力0.01mg，瑞士METTLER TOLEDO公司)；微孔过滤器(0.45μm，美国Whatman公司)；单标线容量瓶(50mL、100mL，A级，北玻)；超声波清洗器(昆山超声波仪器公司)。

3.3　色谱条件

流动相：乙腈+水=60%+40%(体积分数)真空抽滤，装于棕色瓶，用超声波脱气；色谱柱：ZORBAX Eclipse Plus C18柱(250mm×4.6mm，5μm)；柱温：40℃(温差变化应不大于2℃)；流速：1.0mL/min；检测波长：245nm；进样量：10μL。

3.4　检测步骤

试样处理：准确称取M=100mg试样于50mL的容量瓶中，加入少量的乙腈，超声溶解，静置室温后定容。测定时，经有机膜过滤。

标准曲线绘制：分别称量28.89、32.09、36.02、40.14、44.20、48.24、52.40(mg)的标准品(RM)于50mL的容量瓶中，加入乙腈溶解定容。分别进样检测，得到标准曲线的直线方程。

定量测定：将待检试样溶液同样进样检测，由其响应值从直线方程可得到试样溶液浓度cp，再计算得试样中唑酮草酯含量X。

(3)

式中：X为唑酮草酯百分比含量；M为试样称样量；V为定容体积。

4结果

4.1　标准曲线绘制

唑酮草酯线性关系数据见表2和图2。采用最小二乘法拟合，得直线方程为：

A=14259c-151.14,R2=0.9997。

(4)

表2　标准溶液浓度及相应的峰面积

图2　唑酮草酯标准线性曲线

4.2　试样检测

将试样对应的峰面积代入直线方程(4)，求出相应的浓度。再利用方程(3)，计算含量，试样10次平行测定的结果如表3所示。

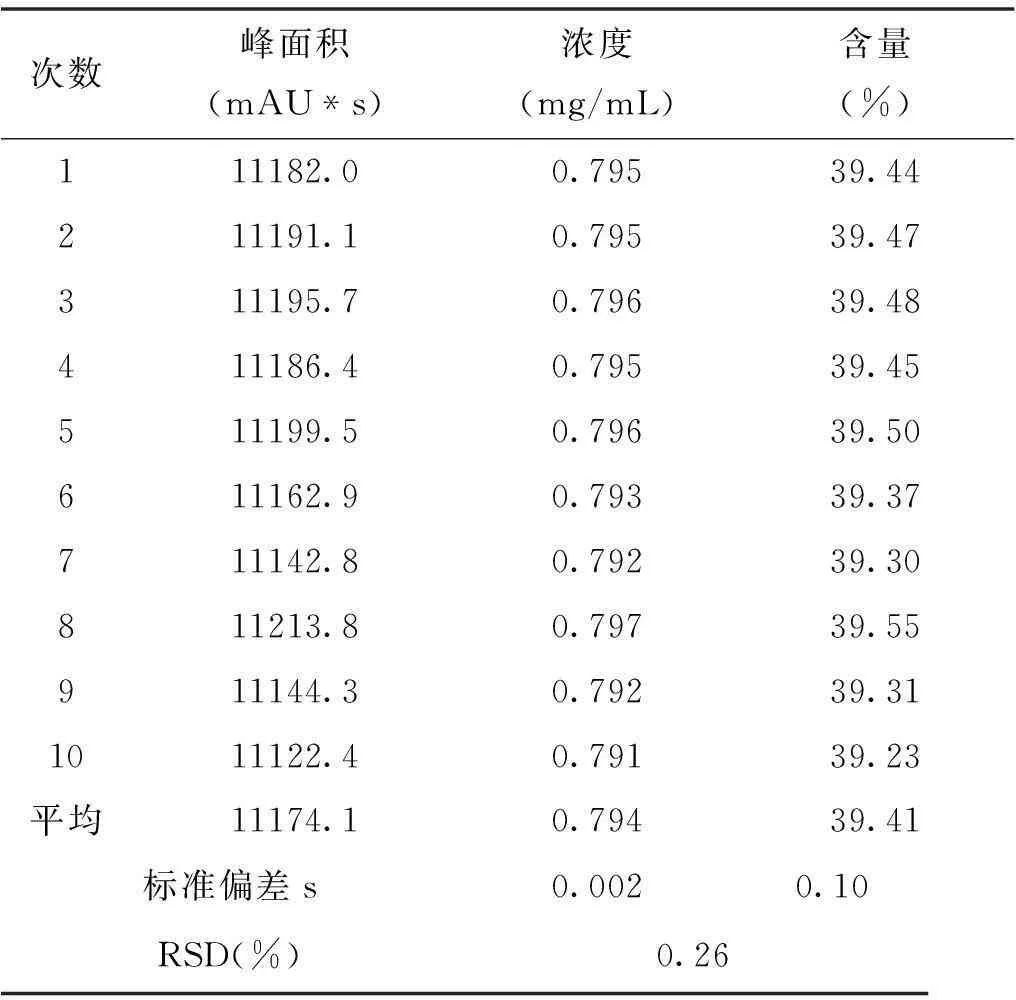
表3　试样的峰面积及相应的浓度和含量

4.3　回收率测定

在空白制剂中，采用加标法(0.892mg/mL)多次累计测得回收率结果见表4。

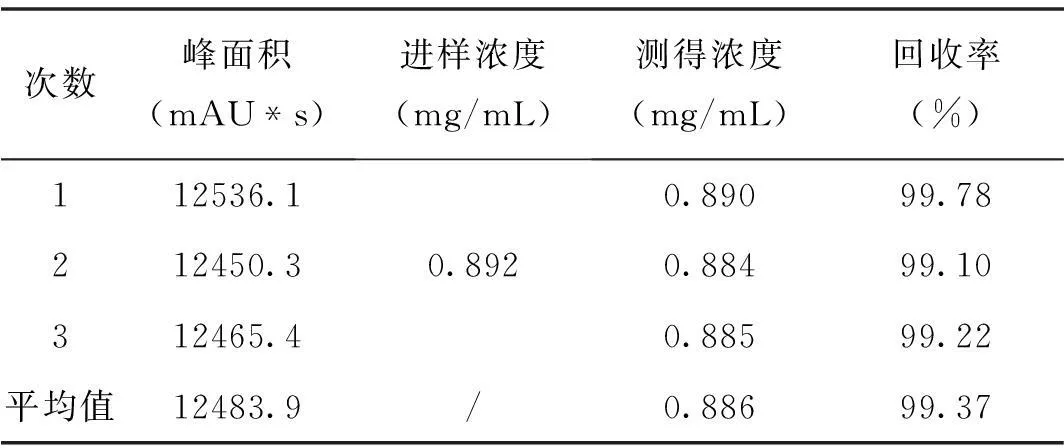
表4　回收率测定结果

4.4　输入量的标准不确定度评定

根据实验的测量方法及数学模型，影响农药制剂产品唑酮草酯含量测定的不确定度分量有5种。

4.4.1试样浓度引入的标准不确定度urel(cp)

urel(cp)主要由RM纯度、称量、定容配置的标准溶液浓度不准引起，以及最小二乘法制作拟合标准溶液浓度—峰面积曲线中随机因素引起的。

4.4.2试样质量引入的标准不确定度urel(M)

主要由称重时天平最大允许误差(MPE)构成。

4.4.3试样溶液体积引入的标准不确定度urel(V)

主要由定容体积，即容量瓶体积的不准引入。

4.4.4回收率引入的标准不确定度urel(R)

本实验采用方法回收率对制样过程进行不确定度评价。

中华优秀传统文化积淀着多样、珍贵的精神财富。传承发展中华优秀传统文化，就要大力弘扬有利于促进社会和谐、鼓励人们向上向善的思想文化内容。《论语》成书于春秋战国之际，是孔子的学生及其再传学生所记录整理而成，记载了孔子及其弟子的言行，是儒家学说的重要文献。书中关于德育的内容全面系统，博大精深，不仅在当时是一部德育的奇书巨作，甚至在今天，对于培育和践行社会主义核心价值观，培养能够担当民族复兴大任的时代新人，建设社会主义文化强国仍然具有重大的指导意义。

4.4.5重复性引入的标准不确定度urel(r)

主要由测量系统的测量重复性引入。

4.4.6数学模型

测定结果和有关参数有以下函数关系[8]：

(5)

式中：R为回收率(R=1)；r为测量重复性修正系数(r=1)。

4.4.7标准不确定度评定结果

各不确定度分量相互独立，不相关，结果见汇总表5。因此农药制剂产品39.7%唑酮草酯可湿性粉剂的检测结果的扩展不确定度可用公式(6)进行计算。

Urel(X)=

(6)

表5　输入量标准不确定度汇总表

5结论

利用标准样品(RM)可以给试样准确赋值的特点，结合测量能力指数(MCP)对测量过程控制分析的特性，提出一种基于MCP和RM的检测质量评估新方法。该方法利用试样的量值为目标值预测解决了检测误差评价的一致性问题，同时MCP能更好地实现实验室内部质量监控。实验结果表明该方法在各实验室测量系统检测结果趋同性方面优于传统的其它检测质量评价算法。

参考文献

[1] Kotz S,Johnson N L. Process capability indices-a review,1992-2000/discussion[J].Journal of Quality Technology, 2002,(01):2-53.

[2] 孙小素. 过程能力指数研究综述[J]. 山东工商学院学报. 2010, 5(24): 32-26.

[3] 王维峰,孙梦翔,王继忠,等. 一种新型宽量程气体流量标准装置的研制[J]. 自动化仪表,2012(6):18-25.

[4] Fred Spiring. A Process Capability/Customer Satisfaction Approach to Short-run Processes [J]. Quality and Reliability Engineering International, 2008, 24: 467-483.

[5] 王维峰,施江焕. 测量能力指数在计量比对中的应用[J]. 计量技术, 2014. 4:66-69.

[6]赵延明,刘德顺,曾磊. 基于服役寿命分布的产品质量损失建模[J]. 机械工程学报,2012,(20):182-191.

[7] Teran A,Pratt D B,Case K E.Present worth of external quality losses for symmetric nominal-is-better qualitycharacteristics[J].The Engineering Economist,1996,42(1):39-52.

[8]田玉平,王虎,蒋和平. 高效液相色谱法测定乳及乳制品中三聚氰胺含量的不确定度评定[J]. 实验室研究与探索,2010(01): 41-43.

[9] Peng H P, Jiang X Q, Xu Z G, et al.Optimal tolerance design for products with correlated characteristics by considering the present worth of quality loss [J]. Int J Adv Manuf Technol, 2008(39): 1-8.

[10] Chou C Y, Chang C L. Minimum-loss assembly tolerance allocation by considering product degradation andtime value of money [J]. Int J Adv Manuf Technol, 2001(17): 139-146.

[11] 曹衍龙,杨将新. 模糊质量损失模型的建立与应用[J].农业机械学报,2004,(04):132-135.