基于蒙特卡罗仿真的汇聚冲突风险评估

基于蒙特卡罗仿真的汇聚冲突风险评估*

郑乐隋东▲林颖达张军峰

(南京航空航天大学民航学院南京210016)

摘要为了揭示汇聚交通场景中冲突风险的总体水平以及动态变化规律，提出了基于蒙特卡罗仿真的汇聚交通流冲突风险评估方法。通过分析汇聚航路的几何特性，构建了汇聚交通流的冲突航段模型，从而确定汇聚交通流产生冲突的范围。并设计了基于蒙特卡罗仿真的冲突风险评估方法，通过实时对比四维轨迹，对冲突率、冲突严重程度、冲突风险、总冲突风险等指标进行了评估,实现了对汇聚交通流从局部到整体,从宏观到微观的冲突风险分析。最后，针对A593航路与R343航路在VMB点汇聚的实际汇聚交通场景，在分析实际运行数据分布的基础上对其冲突风险进行了评估。

关键词航空运输；风险评估；冲突；汇聚交通流；蒙特卡罗仿真

中图分类号：V355文献标志码：A

收稿日期：2015-04-13修回日期：2015-05-22

基金项目*国家自然科学(批准号：71401072)、江苏省自然科学

作者简介：第一郑乐(1990-)，硕士研究生. 研究方向：空中交通安全. E-mail: yue_zheng@nuaa.edu.cn

An Assessment of the Conflict Risk of Converging Air

Traffic using Monte Carlo Simulation

ZHENG YueSUI DongLIN YingdaZHANG Junfeng

(CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing, 210016,China)

Abstract:In order to unveil the overall states and dynamic variation of conflict risks for converging air traffic, a conflict risk assessment method based on Monte Carlo simulation was proposed. Based on the analysis of the geometry characteristic of the converging airways, the conflict route segment model is proposed to determine the conflict ranges that are caused by converging air traffic. The conflict risk assessment method based on the Monte Carlo Simulation was designed. The conflict risks of converging air traffic were assessed from macroscopic and microscopic levels by comparing the 4D trajectories, conflict rate, conflict severity, conflict risk and total conflict risks. Finally, the conflict risks were assessed for the convergence of Route A593 and Route R343 at VMB by the simulation as an example based on statistical analysis of historical operation data.

Key words:air transportation; risk assessment; conflict; converging air traffic; Monte Carlo simulation

▲通信作者：隋东(1971-)，博士，副教授. 研究方向：空中交通安全. E-mail: dong_sui@nuaa.edu.cn

0引言

近年来，随着空中交通流量的不断增长，飞行冲突频繁发生，对基于雷达引导的管制指挥提出了严峻挑战。而终端区作为承担飞越交通流、进离场交通流的复杂区域，其飞行冲突较为突出，其中以汇聚交通流之间的冲突最为常见。因此，无论是为了保障目前的安全运行，抑或是指导未来的空域规划与航路结构调整，分析与评估此类飞行冲突都显得尤为迫切。

随机过程理论[1]、混杂系统理论[2]，以及蒙特卡罗仿真[3]广泛应用于冲突探测领域，其主要目的在于探测冲突是否发生，以及如何降低冲突探测的误报率与漏报率。而冲突风险评估旨在研究冲突的发生、发展与消散的内在机理，国内外诸多学者针对该领域进行了如下研究：David[4]使用圆形保护区模型对交叉航路的单位小时冲突数量进行评估；Wim[5]以航空器对之间的椭球距离为基础，提出了飞行冲突严重度和飞行冲突累计风险的数学模型。Friedman[6]将冲突持续时间作为考虑因素用于分析冲突风险；赵洪元[7]根据同一高度的2条交叉航路的冲突区域，提出了交叉航路间隔模型，并应用其计算交叉航路冲突次数。Netjasov[8-10]分别从战略、战术、及运行层面建立冲突风险模型，战略层面主要从冲突概率和冲突数量这2个指标对飞行程序的宏观冲突风险进行评估。战术层面提出了冲突持续时间和冲突严重程度的概念，对冲突的规律和机理进行升入研究。运行层面将管制员的情景意识、工作负荷作为考虑因素，可用于辅助空中交通管理者对扇区的合并与分开进行决策。以上的冲突风险评估方法通常是在对空域结构分析的基础上，对交通流量和航空器的飞行状态提出了很多简化的假设，并没有从运行的角度出发考虑交通量的分布、航空器运动状态的变化、以及航空器的性能差异等因素，无法对冲突的微观层面的进行细致的描述。

笔者从航空器的实际运行角度出发，首先针对汇聚航路的几何特性提出了汇聚航路的冲突航段模型。然后设计了冲突率、冲突严重程度、冲突风险、总冲突风险等指标。最后在对交通流特性分析的基础上，设计了基于蒙特卡罗卡罗仿真的冲突风险评估方法，并对实际汇聚场景的冲突风险指标进行了评估。

1冲突航段模型

航路航线几何构型不同，导致航空器冲突类型各异，包括：追赶冲突、交叉冲突以及汇聚冲突。终端空域常见多条进场航线汇聚成1条以完成进近着陆的情况，因此本节主要研究汇聚冲突类型。如图1所示，汇聚后的航线3潜在冲突主要体现在由于航空器速度不同而形成的追赶冲突，这与

航空器当前速度，以及性能有关，其本质上仍属于在同1条航线上航空器之间的内部冲突，并不属于航线汇聚而形成的冲突，因此提出了1种分析汇聚航线潜在冲突区域的模型——冲突航段模型。

如图1所示，进场航线1和航线2在P点汇聚，汇聚后形成1条新的航线3，其中航线1和航线2之间的夹角为α，航线3与航线1的夹角为β，水平的冲突间隔标准定义为Smin。

图1　汇聚交通流示意图 Fig.1　Diagram of converging air traffic flow

假设在航线1上运行的航空器i在t时刻处于汇聚点P的位置。以Smin为半径划设圆形保护区，直线l1和l2是航线1侧向保护区的边界。选取航线1为基准交通流，航线2则为相关交通流，在此条件下确定冲突航段|P1P2|的长度。|P1P2|之外的非冲突航段能满足如下条件：

1)在t时刻之前的任一时刻，航线2的非冲突航段上任意航空器j与航线1上的航空器i未曾发生冲突，见图2(a)。

2)在t时刻，航线2的非冲突航段上任意航空器j与航线1上的航空器i不存在冲突，见图2(b)。

3)在t时刻之后的，由于航空器i已经处于航线3上，潜在冲突主要体现在交通流中不同速度的航空器追赶而形成飞行冲突，不作为考虑对象。

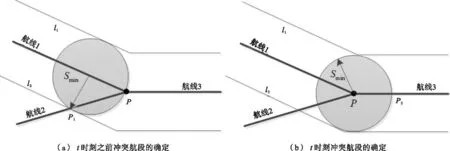
图2　冲突航段的确定 Fig.2　Determination of the conflict route segment

因此，航线2上所有在|P1P2|之外的航空器均不可能与航线1上的某一航空器i在现在、过去以及将来产生冲突。显然，航线2上冲突航段长度D为

(1)

由式(1)可见，汇聚冲突航段长度仅与采取的安全间隔标准Smin以及交叉角α有关，而与β无关。

2基于蒙特卡罗仿真的冲突风险模型

2.1冲突风险指标

冲突航段模型仅仅确定了由于冲突产生范围，至于冲突发生、发展与消散的内在机理需要定义相应的指标予以衡量。以往冲突风险评估主要以冲突次数或冲突频率为评价指标，未涉及冲突演化趋势。毕竟当冲突发生时，航空器之间的间隔会随时间动态变化，而且针对不同的冲突场景，其发生、发展和消散具有显著特性。因此，需要从实际运行出发，设计能够反映冲突风险宏观与微观特性的评价指标。

针对上述情况，本节定义了冲突率、冲突严重程度、冲突风险、总冲突风险等基础指标，从宏观和微观两个角度对冲突的发生以及发展进行更为细致的描述。

2.1.1冲突率

冲突率表征了航空器运行时发生冲突的可能，可以粗略地描述具体场景下的总体冲突水平。冲突率定义为在没有管制员干预的情况下发生的潜在冲突次数和最大可能冲突次数的比值，对于2条航线汇聚的冲突场景而言，其冲突率的计算为

(2)

式中：m为沿着航线1飞行的航空器总量；n为沿航线2运行的航空器总量；Nc是发生的潜在冲突次数。

2.1.2冲突严重程度

潜在冲突的严重程度取决于飞机对间距离在动态变化过程中的最小间距和规定的水平安全间隔标准。冲突严重程度表征了航空器对在水平间隔和垂直间隔都不满的情况下航空器的接近程度。

在水平面上的冲突严重程度定义为

(3)

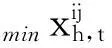
在垂直面上的冲突严重程度定义为

(4)

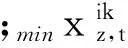
2.1.3冲突风险

冲突风险综合考虑了冲突的发生概率以及严重程度，从微观的角度反映了航空器之间距离动态变化。为了综合描述航空器对之间的距离，本文使用椭球距离来计算航空器之间的接近程度，其计算公式如下。

(5)

式中：a，b，c分别为航空器纵向、侧向、以及垂直方向上的最低安全间隔；Δxi,j，Δyi,j，Δzi,j分别为航空器i和j之间的纵向距离、侧向距离、以及垂直距离。

图3给出了飞行冲突发生、发展和消散的典型过程。航空器i和航空器j相互迫近，在t1违反间隔后发生冲突，此时的椭球距离小于1；在t*达到最接近点,此时的椭球距离εmin；然后相互分离，在t2再次满足间隔标准的动态过程，此时的椭球距离大于1。

图3　冲突的发生和发展示意图 Fig.3　Evolvement of the conflict

其中，阴影部分的面积定义为

(6)

航空器i与航空器j的冲突风险定义为阴影部分面积与冲突时间，以及总运行时间乘积的比值。

(7)

考虑到航空器i在飞行过程中可能与多架其它航空器发生冲突，其冲突风险定义为

(8)

2.1.4总冲突风险

基于上述单个航空器的冲突风险，提出了总冲突风险的概念，用来表征单位时间内冲突航段内的总体冲突水平，考虑到冲突都是发生在一对航空器之间，因此定义其计算公式如下。

(9)

式中：R*为总的冲突风险；m+n为仿真过程中总的航空器数量。

2.2冲突风险评估

由于在实际的空管运行中规定了诸多的间隔标准，而且空中交通管制员通过管制自动化系统可以实现对航空器的态势监视与间隔调配，因此航空器之间发生冲突属于小概率随机事件。蒙特卡罗模拟[11](Monte Carlo simulation)作为处理随机事件的经典方法，将应用于本文提出的冲突风险评估模型中：基于对空中交通流分布特性进行统计分析，采用蒙特卡罗模拟仿真随机生成大量交通流，计算其冲突风险指标，从而实现冲突风险评估。

由于航空器运动状态的变化、以及各类机型性能差异等因素都会对冲突的产生、消散和发展过程产生影响，因此如何对交通流的运动轨迹进行精确的描述至关重要。笔者利用航空器基础资料[12](base of aircraft data，BADA)中提供的机型性能数据，联合航空器动力学、运动学以及意图模型生成航空器的运动轨迹[13]。

图4为进场汇聚场景下生成的各机型的三维轨迹示意图，轨迹生成过程中根据过点的高度限制、速度限制以及是否为转弯点，将航空器的运动状态分成了5种，包括：旁切转弯、减校正空速下降、减校正空速平飞、等校正空速下降、等校正空速平飞。由于各类型航空器之间性能上的差异，运动状态之间切换的时机各不相同。

图4　各机型三维轨迹示意图 Fig.4　3D trajectories of the different kinds of aircraft type

针对上文所提到的冲突风险指标，设计了基于蒙特卡罗的汇聚交通流冲突风险评估方法，其基本流程见图5，具体流程如下。

图5　蒙特卡罗仿真流程图 Fig.5　Flow chart of the Monte Carlo simulation

1)设定蒙特卡罗仿真的次数。

2)根据仿真次数随机生成飞行计划，包括所执行的航路信息、航班出现时间、以及机型信息。

3)根据飞行计划中的航路信息读取航路数据库，读取相应的航路对应点的信息，包括点的经纬度、是否为转弯点等，作为航班的飞行意图。

4)针对特定的机型和航路，根据对历史雷达数据统计得到的高度、速度限制的均值和方差随机生成相应的高度、速度限制作为航班的航空器意图。

5)将航班的飞行意图和航空器意图作为轨迹生成模型的输入生成航空器的轨迹，轨迹生成步长设置为△t。

6)对于任意t时刻各航班的四维轨迹，进行两两比较判断冲突，记录冲突航空器对的航班号、冲突发生时间、以及间隔等冲突信息。

7)根据记录的冲突信息实现冲突风险评估。

3仿真验证

3.1仿真场景描述

如图6所示，仿真选取A593航路与R343航路在VMB汇聚的场景进行实例分析。截取了A593航路中PIMOL到VMB航段，对于起始点命名为VMB UP.同样截取了R343航路中从GS到VMB航段，对于起始点命名为VMB DOWN，2条航路汇聚后沿着A593航路直至EKIMU，2航路夹角为50.7°。

图6　汇聚场景描述示意图 Fig.6　Diagram of the actual converging scenario

假设水平安全间隔标准Smin=10km，应用式(1)所示冲突航段模型可得D=22.9km，其中P1P=12.9km，PP2=10km，图6中黑色矩形为冲突航段边界。

3.2历史数据分析

3.2.1高度/速度限制的提取

分析2013年1月2日至8日经由上述两条航路的897架航班雷达轨迹。其中，沿A593飞行的航空器共219架次，R343共678架次。以经由R343航路飞行的航班为例，对其过点的高度，速度的均值以及方差进行统计，如图7所示，构建航空器意图模型。

3.2.2航班时间间隔分布

由于航空器的出现可以近似看作是相互独立的随机事件，所以可以假设进港时间间隔服从指数分布，即单位时间的航班量服从Poisson分布。使用指数分布对航班的出现时间间隔的进行拟合。以VMB DOWN为例，通过和指数分布进行拟合求得指数分布的数学期望μ=473。图8为和指数分布拟合的概率密度曲线，以及概率累积曲线。同理可以求得VMB UP时间间隔对应的指数分布的数学期望为μ=972。

图7　进场汇聚航班高度速度限制示意图 Fig.7　Diagram of arrival altitude & speed profile

图8　航空器出现时间间隔分布与指数分布的拟合 Fig.8　Fitting diagram of the time inreval

3.2.3机型分布

对897架航班的机型数据进行提取，共存在21种机型，各机型的数量分布见图9。

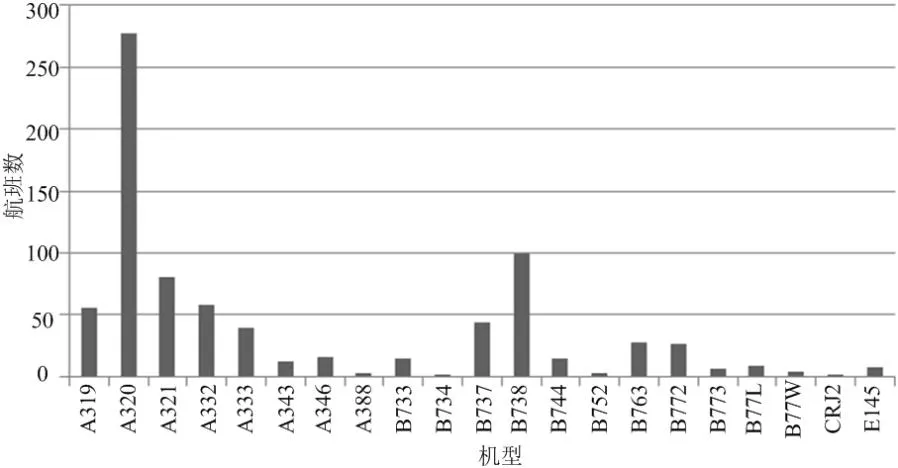
图9　机型分布 Fig.9　Distribution of the aircraft types

3.3仿真结果分析

基于Java编程语言、利用MySQL数据库和ArcGIS软件设计开发蒙特卡罗仿真工具,轨迹生成步长设置为△t= 2s，主界面见图10。仿真工具在对交通量的分布进行统计分析的基础上，细致的考虑了航空器的高度、速度变化以及各航空器之间的性能差异,相对于传统的冲突风险分析大大提高了模型的精度，但未考虑由于飞行原因所造成的偏航迹误差现象。

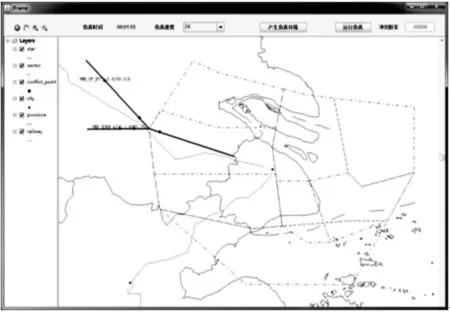
图10　蒙特卡罗仿真工具主界面 Fig10　Interface of the Monte Carlo simulation tool

设定仿真航空器总数为100，出现的时间间隔分布以及机型分布服从上文中的统计值，轨迹的高度速度限制根据过各点的均值及方差随机分配，Smin=10kmHmin=300m，基于图5的流程对该场景进行了仿真。

在仿真过程中，沿着A593航路运行的航班数m=34，沿R343运行的航班数n=66。仿真持续时间T=31790s，共产生8次飞行冲突，冲突率μc=0.00357，总的冲突风险R*=0.0001。各冲突航班的冲突严重程度以及冲突风险见表1。

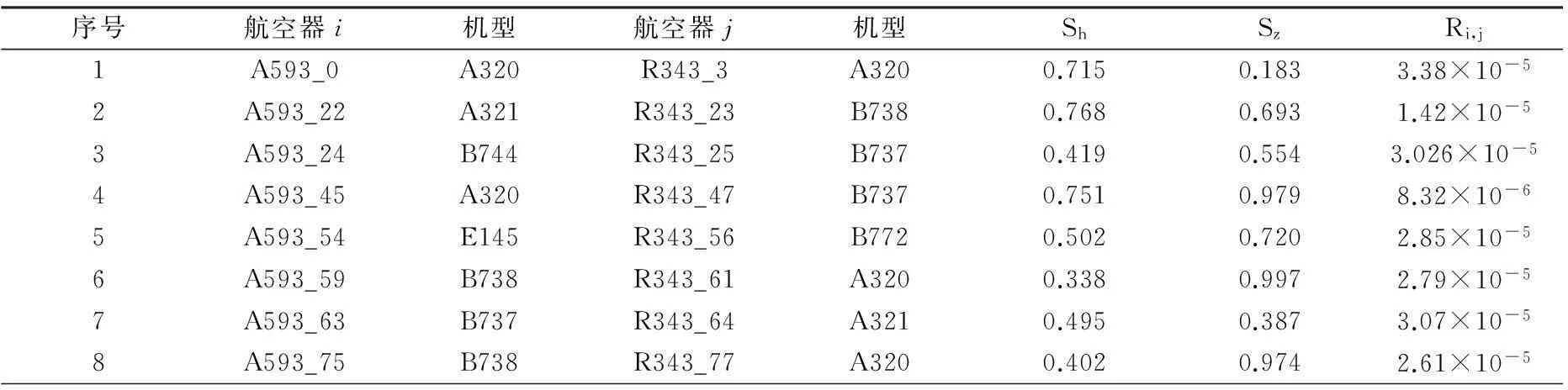
表1汇聚飞行航班的冲突严重程度和冲突风险

图11为航班A593_0与航班R343_3冲突发

图11　汇聚飞行的椭球距离随时间变化趋势 Fig11　Evolvement of the converging conflict

生前后的椭球距离详细变化过程，在t1=356s时，椭球距离首次小于1，冲突发生。t*=377s时，εmin=0.78，此刻2架航空之间的水平距离为3.3km，高度相差245m。t2=382s时，冲突结束，但2架航空器仍然处于较接近的状态。由此可见，对于汇聚冲突而言，由于2架航班汇聚后任然沿着同一条航路同向飞行，由于航空器速度之间的差异不会使得冲突迅速消散，因此冲突的持续时间相对较长，具有较高的安全风险。

4结束语

介绍了基于蒙特卡罗仿真的汇聚交通流冲突风险评估方法，可以根据实际航班运行特性对该场景下的冲突进行局部到整体、宏观到微观的分析。不仅可以为飞行程序的设计的优化提供借鉴，还有助于对空管运行过程中的冲突风险进行科学分析。本文使用的随机过程仿真的方法不仅适用终端汇聚航路的冲突的研究，还可以进一步扩展分析航路中的交叉冲突以及由于追赶而产生的冲突。为了更好的模拟航空器轨迹运行，将航空器偏航迹误差作为随机量增加到仿真过程当中将是下一步研究工作的方向。

参考文献

[1]LAUDERDALE TA. Probabilistic conflict detection for robust detection and resolution[C]. AIAA 12th Aviation Technology, Integration and Operations Conference, Indianapolis, USA:AIAA ,2012.

[2]LIU W, HWANG I. Probabilistic trajectory prediction and conflict detection for air traffic control[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1779-1789.

[3]GUO H, ZHANG J, ZHU Y. Conflict detection and avoidance based on CPDB for free flight[C].AIAA Guidance, Navigation, Control Conference, Portland, Oregon: AIAA, 2011.

[4]SCHMIDT D K. On the conflict frequency at air route intersections[J]. Transportation Research, 1977, 11(5): 351-355.

[5]WIM D B. Analysis of aircraft/air traffic control system performance[C]. Proceedings of AIAA Guidance, Navigation and Control Conference, Baltimore, MD: AIAA,1995.

[6]FRIEDMAN M F. On the frequency of the perceived conflicts with prescribed duration at intersecting air routes[J]. Transportation Research Part B: Methodological, 1984, 18(4): 329-337.

[7] 赵洪元. 两条交叉航线上飞机发生危险冲突次数模型的研究[J]. 系统工程与电子技术， 1998, 20(5): 6-8.

ZHAO Hongyuan. Study on the model for computing the number of dangerous conflicts among aircrafts on two intersecting tracks[J]. Journal of Systems Engineering and Electronics, 1998, 20(5): 6-8. (in Chinese)

[8]NETJASOV F. Framework for airspace planning and design based on conflict risk assessment: Part 1: Conflict risk assessment model for airspace strategic planning[J]. Transportation Research Part C: Emerging Technologies, 2012(24): 190-212.

[9]NETJASOV F. Framework for airspace planning and design based on conflict risk assessment: Part 2: Conflict risk assessment model for airspace tactical planning[J]. Transportation Research Part C:Emerging Technologies, 2012(24): 213-226.

[10] NETJASOV F, BABIC O. Framework for airspace planning and design based on conflict risk assessment: Part 3: Conflict risk assessment model for airspace operational and current day planning[J]. Transportation Research Part C: Emerging Technologies, 2013(32): 31-47.

[11]STROEVE S H, BLOM H A P, BAKKER G J. Systemic accident risk assessment in air traffic by Monte Carlo simulation[J]. Safety Science, 2009, 47(2): 238-249.

[12]Eurocontol Experimental Center. User manual for the base of aircraft data (BADA), revision 3.10. EEC Technical/Scientific Report No. 12/04/10-45[R]. Brétigny: EEC, 2012.

[13]张军峰，蒋海行，武晓光，等. 基于 BADA 及航空器意图的四维航迹预测[J]. 西南交通大学学报，2014， 49(3)：553-558.

ZHANG Junfeng, JIANG Haihang, WU Xiaoguang, et al. 4D trajectory prediction based on BADA and aircraft intent[J]. Journal of Southwest Jiaotong University, 2014, 49(3): 553-558. (in Chinese)