单机鲁棒性最小提前期研究
单机鲁棒性最小提前期研究
苏燕妮,王巍*,张永智
(东北林业大学 工程技术学院,哈尔滨 150040)
摘要:现代加工制造生产实际生产环境中有很多不确定因素,为了提高企业生产效率,提高生产调度的稳定性,保证生产的有序、高效进行,针对订单式加工单机生产过程中新产品初始加工参数错误的情况,本文以最小提前期为目标,首先对鲁棒性测度进行说明,根据单机鲁棒性对其最小提前期进行确定,并且对问题进行分析,然后构建了以EDD为原则的初始调度模型与平均提前时间的优化调度模型。运用插入空闲加工时间的方法,保证优化调度满足鲁棒性测度,并且对初始调度方案以及优化调度方案通过Matlab软件分别进行模型仿真验证,仿真结果表明该方法应用下的优化调度模型的适用性和有效性。得到结论:该模型有效的支持最小提前期单机生产优化调度。
关键词:单机;最小提前时间;鲁棒调度
中图分类号:S 782;Q 223
文献标识码:A
文章编号:1001-005X(2015)02-0125-05
Abstract:There are many uncertain factors in the modern manufacturing production environment.In order to improve the production efficiency and stability of production scheduling and ensure the orderly and efficient production,and according to the situation of initial processing parameter error for new products in order-based single production process,this paper sets the minimum earliness as the goal,firstly,explains the robustness measurement and determines the minimum earliness based on single-machine robustness in advance,and build up the initial scheduling model based on EDD principle and set a scheduling model which considers the case of the average error.Based on the inserting idle processing time method,the optimal scheduling was obtained to meet robustness requirement.The initial scheduling scheme and optimal scheduling scheme were simulated by Matlab,and the simulation results showed the applicability and effectiveness of the optimized scheduling model.It is concluded that this optimal scheduling model can support a minimum earliness single-machine production effectively.
Keywords:single-machine;minimum earliness;robustness scheduling
收稿日期:2014-09-19
基金项目:黑龙江省留学归国科学基金项目(LC201407)
作者简介:第一苏燕妮,本科生。研究方向:生产与运作管理。
通讯作者:*王巍,博士,副教授。研究方向:工业工程。E-mail:cedar3@163.com
Single-Machine Robustness Scheduling with Minimum Earliness
Su Yanni,Wang Wei*,Zhang Yongzhi
(College of Engineering and Technology,Northeast Forestry University,Harbin 150040)

引文格式:苏燕妮,王巍,张永智.单机鲁棒性最小提前期研究[J].森林工程,2015,31(2):125-129.
实际生产过程中存在的各种不确定因素,如机器故障、加工时间波动、紧急订单和返工等,可能会扰乱初始调度,影响调度目标的实现。根据对不确定因素的掌握程度,通常将其分为完全未知、部分已知和完全已知不确定因素三类[1]。完全未知不确定因素没有任何可用信息,在有这种不确定因素干扰的情形下,一般使用反应式调度。新产品初始加工参数错误多数属于完全已知不确定因素。生产调度的鲁棒性通常分为性能鲁棒性和调度解鲁棒性两类。性能鲁棒性是指初始调度在不确定因素扰动下的实际调度目标与实际最优调度目标的接近程度,两者越接近,初始调度的性能鲁棒性越好;调度解鲁棒性是指不确定因素扰动下的实际调度方案与初始调度方案的接近程度,两者越接近,调度解鲁棒性越好[2-3]。
在过去的研究中,对于在生产过程中存在新产品初始加工参数错误的调度问题,各学者和工程技术人员进行了广泛的研究。由于生产之前无法获得实际数据,Selcuk Goren等[4]给出了两种替代测度,并且利用实际案例说明了替代测度对鲁棒调度是有效的。新产品初始加工参数错误则会导致订单加工取消,带来大量的空余时间,而根据新产品初始加工参数错误带来的提前时间插入空闲时间也是一种比较有效的调度方法,文献[5]在给出三种空闲时间度量方法的基础上,研究了插入空闲时间的鲁棒调度算法,并且给出了在调度性能和鲁棒性之间进行权衡的方法。对于新产品初始加工参数错误下鲁棒调度问题的研究,许多人关注其调度的鲁棒性,但调度的鲁棒性与调度性能往往互相牵制、互相影响。本文研究机器故障环境下的调度问题1|rj|Tmax的棒调度方法,缩小提前时间为目标,研究其优化方法。在对问题进行描述的基础上,首先研究求解在限定鲁棒性约束下使得调度性能目标最优的调度问题,提出Tmax最优调度方法,并给出仿真实例验算,验证本文所提方法的适用性和有效性。
本文的研究为新产品初始加工参数错误环境下单机调度问题提供了提前时间最小的调度方法,在实践中能够减小订单加工参数错误对初始调度的影响,保证在限定的鲁棒性约束下保证初始调度的稳定性,提高调度目标的满意程度。
1鲁棒性指标与问题描述
1.1 符 号
本文主要用到以下符号:
rj为订单j的释放时间即最早可以开工的时间;Pj为订单j的加工时间;Sj为订单j的开工时间;dj为订单j的交货期;cj为订单j的完工时间;T为平均提前时间;t为订单无法加工的平均时间间隔;σ(k)为调度中σ第k个位置的订单;σp为初始调度;Cmax(σ)为调度σ的最迟完工时间;Dj(σp)为实际调度σr与初始调度σp中订单j的期望完工时间差绝对值;Tmax(σ)为调度σ的提前时间,Tmax(σ)=maxj(Cσ(j)-dσ(j));RS为调度的鲁棒性测度;Z为目标函数值,即总提前时间。
1.2 鲁棒性测度
生产调度的性能鲁棒性和调度解鲁棒性有不同的测度方法,性能鲁棒性通常用调度目标的差异度量,而调度解鲁棒性通常用订单的变化、开工或完工时间的差异等度量。Jorge等[1]用实际调度σr与初始调度σp的期望最迟完工时间差作为初始调度σp的鲁棒性测度。因为初始调度σp受不确定因素扰动,剔出订单的后续订单完工时间均会提前,所以有Dmax(σp) ≥0。Ronan O Donovan等[3]用实际调度与初始调度各订单期望完工时间差的绝对值之和表示调度鲁棒性,即
RS=∑Dj(σρ)=E[∑|Cj(σr)-Cj(σp)|]。
公式(1)给出了在订单j加工过程中的机器平均提前时间:
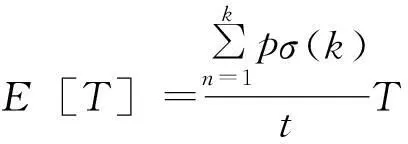
(1)
在订单剔出环境下,调度σ的鲁棒性可以定义为:
∑Dj(σp)=E[∑Cj(σr)-Cj(σp)]。
此时调度σ完成时间为
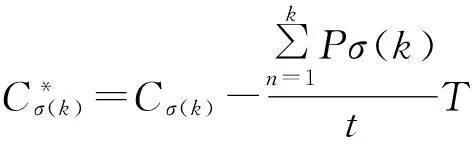
在这种情况下对于鲁棒性最优的调度有
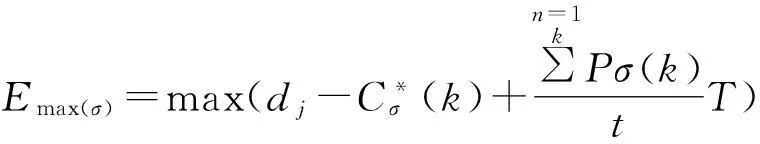
1.3 问题描述
在订单式生产环境下,新单在试生产的过程中,极有可能因为对新产品设计及加工参数把握不当,出现生产错误,此时需要停止生产,对模具进行重新制定或其他处理,整个订单将会取消并延迟生产。此时,后续订单则会提前进行生产,从而产生加工完成时间提前于交期的现象。而停单后的下一笔订单的开始加工时间又会影响本单以及后续订单的完成时间。订单完成时间小于交期会带来库存问题,对于现代制造企业来说,库存即是浪费,能有效的减小成品存放对企业制造成本的减小有举足轻重的作用。所以,应当在调度上合理控制。在保证给定调度鲁棒性约束的前提下,对于调度σ,改变其开工时间,增大或减小订单之间的空闲时间,则鲁棒性也将发生变化,同时调度提前时间Tmax(σ)也将发生变化。求解在以调度鲁棒性为约束性指标时,求解在满足其要求的基础上,使调度性能Tmax(σ)最小的调度方案。
2调度问题1|rj,RS<α|Tmax的求解
在订单式实际生产中,通常要求在限定解鲁棒性最优的调度方案,调度性能目标是最大提前时间,则问题表示为1|rj,RS<α|Tmax。
2.1 初始调度模型建立
调度方案结果显示按照订单交期顺序进行生产,若订单交期一样,则按照订单加工数量多少进行生产,数量多的优先生产,此时调度方案为最优,即“最早交货最早加工EDD”规则。以每笔订单交期与完成时间差值总和最小为目标函数,初始调度方案建立以下数学规划模型(RP):
s.tCσ(j)≥sj+pj
(1)
Cσ(j)≥sj+pj
(2)
Cσ(j)-Cσ(j-1)≥pj
(3)
sj≥Cσ(j-1)
(4)
在该模型中,约束(1)为调度中的单个订单时间约束;约束(2)为相邻两个订单的时间约束;约束(3)为后续订单加工开始时间不得早于前订单结束时间;约束(4)为初始完工时间。
2.2 问题分析
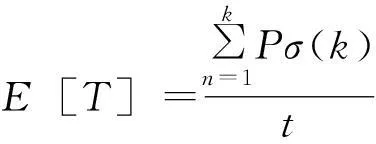
2.3 优化调度模型建立
在考虑平均加工时间的情况下,建立优化调度模型,其目标函数为每项订单完工时间与交期差值的总和,此时完工时间为初始调度方案下完工时间减去平均提前时间。优化调度方案建立以下数学规划模型(RP):
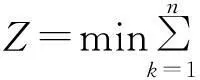
S.t.Cσp(k)≥rk+pk
(1)
Cσ″p(k)-Cσ″p(k-1)≥Pσ″p(k)
(2)
Cσ′p(k)≤σ″p(k)
(3)
Cσ″p(0)=0
(4)
Cσ′p(k)-Cσ″p(k)≤α
(5)
在该模型中,约束(1)为调度σp″中的单个订单时间约束;约束(2)为相邻两个订单的时间约束;约束(3)为各订单完工时间需要延后;约束(4)为设置的虚拟订单完工时间,约束(5)为调度σp″的最大提前时间约束;约束(6)为优化调度与初始调度的鲁棒性测度满足条件。
3仿真分析
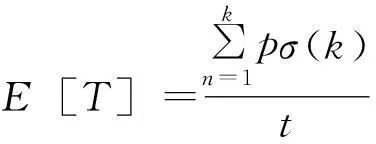
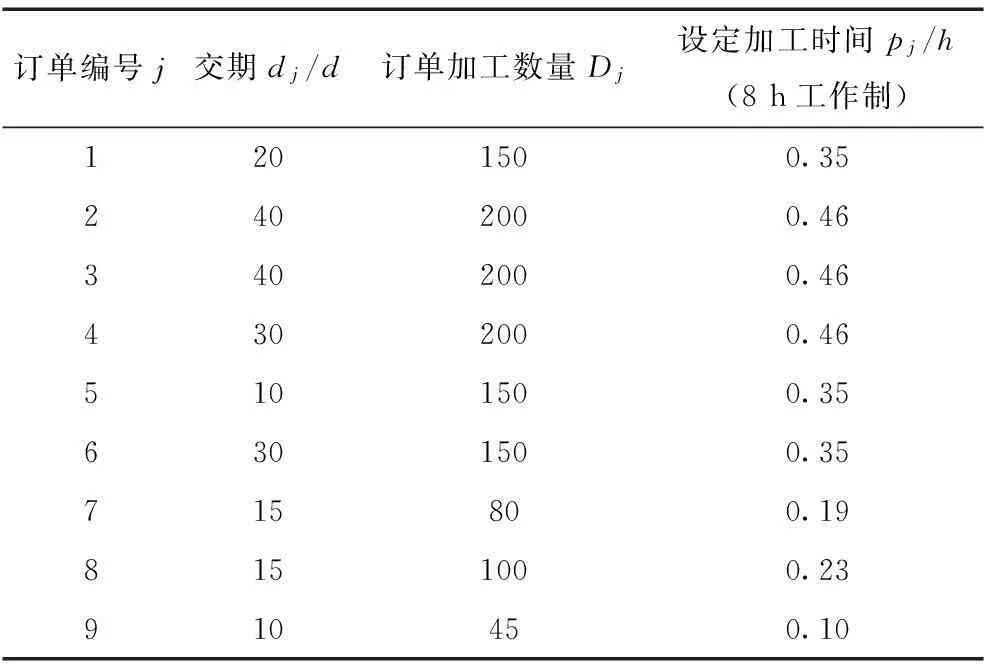
表1 加工订单参数 Tab.1 Processing order data
3.1 初始调度方案
根据2.1中所述建立模型,本文将调度问题的条件和约束抽象为简化的模型表达式,并把调度的评价指标作为调度模型优化的目标,调度方案以“最早交货最早加工EDD”为规则,通过对模型的分析和求解来对的生产调度提供决策方案。为了模型的处理,提出以下假设:
(1)若某一订单开始生产,在没有完成之前,不能进行另外订单的生产,即单机生产方式。
(2)由于时间约束,从开始至生产结束过程中没有停顿,即生产是连续性的。
(3)提前时间不进行取整,即生产完到截止日期差多少时间即为实际提前期。
例如第30 d的订单,到28.5 d完成了,提前日期为1.5 d,而不是一天或者两天。根据建模假设,对初始调度模型进行基本排序,初始调度方案通过Matlab实现,程序片段如下:
clc
clear
k=perms(1∶9);
k_size=size(k);
fori=1∶k_size(1)
i
Cj=0;
Z(i)=0;
forj=1∶k_size(2)
Num=k(i,j);
Pj=Cj+Data(3,Num);
Cj Z(i)=Z(i)+(Data(2,Num)-Cj)*Data(4,Num); end end MinZ=min(Z) j=find(Z<(MinZ+1)); σ=k(j,:) 根据程序生成的最终序列,初始调度方案结果为:5、8、9、7、1、4、3、2、6,目标函数生成提前期的结果为:10.55。以上测试表明,建立的初始调度模型是正确可行的,生产过程存在着较大的生产提前期。 为了控制生产中的不确定性,定义工厂生产参数鲁棒性约束为10%,即要求加工完成时间与交期偏差限定在1.055 d以减少库存成本。按照前文2中所建立的数学规划模型,在考虑平均提前时间的情况下,如调度结果不满于参数鲁棒性约束,则采用交期与完成时间差值最小订单补足空闲时间,使其完成时间等于交期,该订单后续订单最前的开始加工时间则为该订单的交期,后续所有订单按照前文2中的数学规划模型重新排序,直到满足鲁棒性约束。 订单j加工过程中的机器故障平均维修时间为: 对工件参数进行变换,令rj′=rj,pj′=pj+E(Rj),dj′=dj+E(Rj),参照2.3中所述约束及假设建立模型。其主程序片段如下: clc clear Cj′=10.55; k=perms(1∶9); k_size=size(k); fori=1:k_size(1) Z(i)=0; forj=1∶k_size(2) Num=k(i,j); Cj=Cj+Data(3,Num); Cj Z(i)=Z(i)+(Data(2,Num)-Cj)*Data(4,Num); end end MinZ=min(Z) if(Cj′-MinZ)/Cj′<=0.1; Z(i)=Z(i)+(Data(2,Num)-Cj) else Z(i)=Data(2,Num)-Cj; j2((min(Z)))=[]; whilei(i<=9) loc=find(j2((min(Z)))); j=find(Z<(MinZ+1)); end end j=find(Z<(MinZ+1)); σ=k(j,:) 根据文献中的基本算法,所给参数的订单以最小提前时间Tmin(σ)为调度性能目标,得到最优鲁棒调度σ′,其中Tmin(σ)=4.03,如图1所示,优化后的调度方案为:5、1、7、9、8、4、3、2、6。 图1 最优调度 Fig.1 Optimal scheduling 通过最小提前期调度系统仿真的实际效果来看,基本上达到了优化调度的要求,通过比较两组计算结果可以看出,在考虑新产品初始加工参数错误造成的订单剔出后,对后续订单来带提前期影响的情况下,通过优化调度模型,获得新的调度方案,其目标函数值表示的总提前时间明显缩短,优化幅度达61.77%,改方案和模型是切实有效的。鲁棒性RS与调度性能呈现相反的变化趋势,要使鲁棒性更好,调度性能就会变差,表明调度鲁棒性的提高要以降低调度性能为代价。因此,最小提前期调度方案可以给企业的生产管理带来一定的决策依据。 4结束语 新单在试生产或正式投入生产的过程中经常出现的不确定因素,本文针对这一情况,研究了在新单加工出现错误需要剔出的情况下,以调度最大提前时间的单机鲁棒调度优化方法,探讨了在最大提前时间约束下求解最优鲁棒性的方法。在此基础上,给出了单机鲁棒行最小提前调度优化方法,并且仿真验证了该方法的适应性和有效性。本文的研究局限于单机环境,Flow Shop和Job Shop等复杂机器环境下针对机器故障的鲁棒调度问题将是进一步研究的重点。 【参考文献】 [1]Leon V J,Wu S D,Storer R H.Robustness measures and robust scheduling for job shops[J].IIE Transactions,1994,26(5):32-43. [2]Sevaux M,Sorensen K.A genetic algorithm for robust schedules in a one-machine environment with ready times and due dates[J].Quarterly Journal of the Belgian,French and Italian Operations Research Societies,2004,2(2):129-147. [3]O Donovan R,Uzsoy R,Mckay K N.Predictable scheduling of a single machine with breakdowns and sensitive jobs[J].International Journal of Production Research,1999,37(18):4217-4233. [4]Goren S,Sabuncuoglu I.Robustness and stability measures for scheduling:single-machine environment[J].IIE Transactions,2008,40(1):66-83. [5]Briskorn D,Leung J,Pinedo M.Robust scheduling on a single machine using time buffers[J].IIE Transactions,2011,43(6):383-398. [6]张先超,周泓.单机鲁棒调度多目标优化方法[J].计算机集成制造系统,2013,19(10):2459-2466. [7]何正文,刘人境,徐渝.基于随机活动工期的资源约束项目鲁棒性调度优化[J].系统工程理论与实践,2013,33(3):650-659. [8]胡信布,何正文,徐渝.基于资源约束的突发事件应急救援鲁棒性调度优化[J].运筹与管理,2013,22(2):72-79. [9]张宏国,徐晓飞,战德臣.不确定资源约束下项目鲁棒性调度算法[J].计算机应用研究,2009,26(6):2079-2082+2089. [10]魏巍,谭建荣,冯毅雄,等.柔性工作车间调度问题的多目标优化方法研究[J].计算机集成制造系统,2009,15(8):1592-1598. [11]田文迪,胡慕海,崔南方.不确定性环境下鲁棒性项目调度研究综述[J].系统工程学报,2014,29(1):135-144. [12]徐鸣,马龙华,顾江萍,等.一种改进的鲁棒多目标优化方法[J].控制与决策,2013,28(8):1178-1182+1189. [责任编辑:胡建伟]3.2 优化调度方案
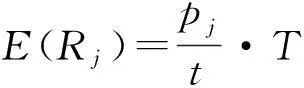

3.3 仿真结果


