利用RPLS算法实现电力系统频率跟踪
利用RPLS算法实现电力系统频率跟踪
李珍珠,王小华,周勇
(长沙理工大学 电气与信息工程学院,湖南 长沙410114)
摘要针对在电力系统频率跟踪算法中推导过程复杂、计算量大等问题,提出了一种利用递推偏最小二乘法(RPLS)实现电力系统频率跟踪的新算法。该方法在递推过程中,采用滑动窗法更新数据,同时引入了适当的遗忘因子。仿真结果表明,该算法在电力系统频率跟踪中具有计算复杂度小,推导过程简单,频率跟踪收敛速度快,测量精度高的特点,其是电力系统频率跟踪中的一种新方法。
关键词RPLS;滑动窗;遗忘因子;频率跟踪
收稿日期:2015-03-03
作者简介:李珍珠(1990—),女,硕士研究生。研究方向:通信和信号处理。E-mail:1179910978@qq.com。王小华(1968—),男,教授,硕士生导师。研究方向:神经网络,信号处理,电力系统谐波分析。周勇(1991—),男,硕士研究生。研究方向:PID,神经网络。
doi:10.16180/j.cnki.issn1007-7820.2015.09.014
中图分类号TM935
Achievement of Frequency Tracking in Power Systems by RPLS Algorithm
LI Zhenzhu,WANG Xiaohua,ZHOU Yong
(College of Electrical and Information Engineering,Changsha University of
Science and Technology,Changsha 410114,China)
AbstractIn view of the complex derivation and large amount of calculation of the power system frequency tracking algorithm,a new algorithm for frequency tracking of power system using a Recursive Partial Least Squares (RPLS) is proposed.The sliding window method is used in the recursive process to update data,and the appropriate forgetting factor is introduced.The simulation results show that this algorithm has small computation complexity in power system frequency tracking with simple derivation,fast convergence and high accuracy.
KeywordsRPLS;sliding window;forgetting factor;frequency tracking
频率是在电力系统保护和控制方案中反应电力系统电能质量的一个重要值。目前,国内外对电力系统频率跟踪算法已经有很多,且文献[1]对这些方法进行了全面的综述。其中,主要的测频算法有解析法[2],DFT算法及改进[3],误差最小化原理类算法[4-5]等。文献[2]提出的算法是解析法求电力系统频率的一种改进,推导电力系统的电压模型是纯正弦波,在非稳态频率的测量中难以适应,且数学推导过程复杂以及存在近似化处理,测量的频率精度不高。文献[3]提出了一种加窗的递推DFT算法,其测量频率的精度高、抗干扰能力强,但是它要求在数据窗和采样率选择合适的情况下才能准确地计算出参数模型值,且文中没有提到计算采样率和数据窗的方法。文献[4]提出了一种基于改进的卡尔曼滤波基波提取算法,该算法抗谐波和噪声的能力强,测量精度高,计算复杂度比一般的卡尔曼滤波算法低,但实行该算法的关键是状态变量、协方差阵初值和模型建立的正确估计,且计算量较大。文献[5]提出的一种可变遗忘因子递推最小二乘法,克服了传统递推最小二乘法抗干扰能力弱、时滞大等缺陷,且结合文献[6]的方法,频率精度和跟踪范围都有了很大的提高,但增大了该算法的计算量。
本文利用电网三点式模型和RPLS算法实行电力系统频率跟踪,该方法是利用Qin[7]改进RPLS算法的思想,结合文献[8]中提到的一种改进算法求取回归系数。同时,为了准确跟踪到频率值,在递推过程中,新数据的更新采用了滑动窗递推法,窗的长度保持不变以及给新老数据块加上遗忘因子,是一种将滑动窗与遗忘因子相结合的方法[9]。分别仿真了频率缓慢变化,频率发生跳变及信号中混有噪声和谐波的3种情况。该方法均能准确地跟踪到频率,证明了利用该方法实现电力系统频率跟踪的合理性和可行性。
1电力系统信号模型
设单相电力系统电压信号模型
v(i1)=Vcos(w1i1Δt+φ)+ξi1
(1)
其中,V是幅值;w1是角频率;φ是相位角;ξi是噪声;i1Δt是瞬时离散时间;w1=2πf1,Δt=1/f2,f1是基波频率;fs是抽样频率。
由文献[10]可知连续3个相邻采样信号之间存在下面的关系
(2)
因此,由式(2)可得
(3)
可将式(3)简写成
yi1=Xi1C
(4)
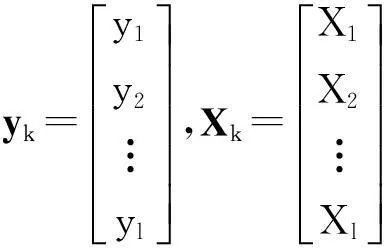
其中,Xi1=[v(i1)/2v(i1-2)/2],C=[1/cos(w1Δt)1/cos(w1Δt)]T,yi1=v(i1-1)。将i1=1,2,….l(l>2)分别代入式(4)中,可得到一个线性等式
yk=XkC
(5)
2RPLS算法实现电力系统频率跟踪
2.1 自适应滤波
在实际操作中,输入信号通常夹带着多次谐波和噪声。因此,需滤波处理。在文献[10]中,2阶滤波的Z 域传递函数可表示为
(6)

由式(6)可知,只需了解基波频率值,便可将相关的滤波系数求出。因此,可得到在不同基波频率下自适应滤波的波形图。

图1 在不同基波情况下的谐波滤波以及采样频率为800 Hz
2.2 RPLS算法实现频率跟踪的原理

(7)
因此,本文利用Qin提出的RPLS算法递推思想。先用样本数据{Xk,yk}计算得到PLS参数{W,P,R,Q}来建立模型。当得到新数据后,将参数模型与新数据结合来更新模型[11]。本文算法不用Qin提出的参数模型解实现递推,而直接将原样本矩阵与新数据相结合来更新模型。
设在式(5)中,取样本个数l个,样本数据矩阵为{Xk,yk},而假设新获得数据矩阵为{Xnew,ynew},可得到递推表达式
(8)

(9)
为了准确地跟踪到频率,对式(9)分别引入适当的遗忘因子λ和λ1,式(9)改写为
(10)
因此,式(10)解决了频率在线递推的问题,而为了求出f,需求出PLS的回归系数C。由文献[15]知,单因变量PLS的回归系数
C=W(PTW)-1QT=RQT
(11)
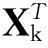
2.3 RPLS算法在频率跟踪中的的具体步骤
(1)信号中存在谐波和噪声时,利用自适应滤波法进行滤波处理。(2)给定电压模型数据矩阵{Xk,yk},并按各变量均值为0,方差为1进行数据预处理。(3)矩阵{Xk,yk}按改进算法[15]计算出PLS所需的参数模型值{W,P,R,Q},具体步骤如下:



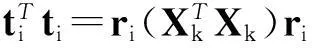
6)存储所有的特征向量W=[w1,w2,…,wi],P=[p1,p2,…,pi],R=[r1,r2,…,ri],Q=[q1,q2,…,qi]。

3仿真分析与结果
本文信号的采样频率为800Hz,采样时间间隔为0.001 25s,初相角是0.1π。RPLS算法实现电力系统频率跟踪从3种情况仿真分析:
(1)图2是在恒定和缓变情况下随时间变化的频率跟踪曲线。设定的恒定实际频率是50Hz,然后再由50Hz缓慢地在49~51Hz之间变化,由图2可知,用RPLS算法能准确地追踪到变化的频率,且其追踪速度快,收敛时间短,说明RPLS算法具有较好的时变性。

图2 由50 Hz缓慢变化到f=50+sin(8πt)的结果
(2)图3显示的是频率在突变情况下随时间变化的曲线图。设定实际频率是50~49.5Hz,结果表明,在延时了约17ms后,用该算法能准确地追到跳变的实际频率。

图3 由50 Hz跳变到49.5 Hz的结果


图4 在谐波和噪声干扰下由50 Hz跳变到51 Hz的结果
4结束语
本文用RPLS算法测量了电力系统频率,为了准确跟踪到实际频率的变化,引入了遗忘因子,既避免了数据饱和的现象,又使得参数的调整更灵活可靠,提高了追踪实际频率的精确度。该算法与电网三点式模型结合只需要求出PLS的回归系数便可解出频率值的思路简单,克服了复杂的数学推导过程,具有计算量小、复杂度低的特点,且在有谐波和噪声的干扰下,进行自适应滤波处理后,仍可较好地跟踪到实际频率,说明其时变性好、鲁棒性强、抗噪性高的特点,是电力系统频率跟踪中一种合理可行的新算法。
参考文献
[1]谢小荣,韩英铎.电力系统频率测量综述[J].电力系统自动化,1999,23(3):54-58.
[2]张超,谭建成.一种基于导数的实时频率跟踪算法[J].电力自动化设备,2007,27(4):32-34.
[3]刘凤新,孔繁征.基于改进DFT变换的高精度实时电网频率跟踪算法[J].电测与仪表,2006(11):6-9.
[4]张斌,张东来.电力系统自适应基波提取与频率跟踪算法[J].中国电机工程学报,2011,31(25):81-89.
[5]陈涵,刘会金,李大路,等.可变遗忘因子递推最小二乘法对时变参数测量[J].高电压技术,2008,34(7):1474-1477.
[6]李振然.利用递推最小二乘算法测量电力系统频率[J].电网技术,1995,19(6):38-44.
[7]QinJoeS.RecursivePLSalgorithmsforadaptivedatamodeling[J].ComputersChemEngineering,1998,22(4):503-514.
[8]DayalBS,MacGregortJF.ImprovedPLSalgorithms[J].Chemometries,1997,54(11):73-85.
[9]汪小勇,梁军,刘育明,等.基于递推PLS的自适应软测量模型及其应用[J].浙江大学学报:工学版,2005,39(5):676-680.
[10]KusljevicMD.Frequencyestimationofthree-phasepowersystemusingweightedleastsquarealgorithmandadaptiveFIRfiltering[J].IEEETransactionsonInstrumMeasure,2010,59(2):322-329.
[11]王勇.基于PLS的建模与控制技术在热工过程中的应用研究[D].保定:华北电力大学,2008.
[12]WoldH.Nonlinearestimationbyiterativeleastsquaresprocedures[M].Newyork:JohnWiley&Sons,1996.
[13]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999.
[14]LindgrenF,GeladiP,WoldS.ThekernelalgorithmforPLS[J].Chemometrics,1993,8(7):45-59.
[15]DayalBS,MacGregortJF.RecursiveexponentiallyweightedPLSanditsapplicationstoadaptivecontrolandprediction[J].ProceedingofControl,1997,7(3):169-179.



