计及UPFC电力系统无功优化研究
通信作者:王佳(1989—),女,硕士研究生。研究方向:电力系统无功优化,无功补偿的智能算法。E-mail:wjwj1123@126.com
计及UPFC电力系统无功优化研究
简献忠,王佳
(上海理工大学 电气工程系,上海200093)
摘要为了更加有效地实现对电力系统潮流分布的控制,以进一步提高电力系统无功优化的有效性,达到使系统损耗最小的目的,提出了基于粒子群智能优化算法的计及UPFC的无功优化方法。以系统有功网损最小为目标函数,为了有效利用UPFC对潮流的调节作用,采用UPFC的节点注入功率模型。通过IEEE-30测试算例就系统有功网损和电压稳定性,对基于粒子群算法系统装设UPFC装置前后进行比较,发现采用文中方法后,不仅降低了系统的有功网损,提高了电压质量,而且与粒子群算法相比,还减少了算法的迭代次数,仿真结果验证了文中模型和算法的有效性和可行性。
关键词无功优化;统一潮流控制器;粒子群算法;电压稳定
收稿日期:2015-02-13
doi:10.16180/j.cnki.issn1007-7820.2015.09.013
中图分类号TM761
Reactive Power Optimization Incorporating Unified Power Flow Controller
JIAN Xianzhong,WANG Jia
(Department of Electrical Engineering,University of Shanghai for Science & Technology,Shanghai 200093,China)
AbstractIn order to control the power flow distribution of power system more effectively,to further improve the effectiveness of the power system reactive power optimization,and to achieve minimizing system loss,this paper proposes a new model based on PSO algorithm for reactive power optimization of a system with UPFC systems.The active network loss minimum is as an objective function using the power injection model of UPFC for effective control of the power flow distribution.This method is implemented and applied into IEEE-30 system and the calculation results indicate that this method not only reduces the active network loss and increases the voltage stability but also reduces the number of iterations of PSO algorithm.Simulation proves the presented model and algorithm are effective and feasible.
Keywordsreactive power optimization;PSO algorithm;unified power flow controller;voltage stability
无功优化是指电力系统在满足安全运行约束的前提下,通过对其控制变量值的优化计算,使系统无功潮流达到最优分布,以达到降低系统损耗、提高电压质量的目的。长期以来,众多专家、学者对此问题进行了大量的研究和探索,从传统算法到智能算法,建立了各种优化模型,如线性规划法、遗传算法、粒子群算法等,这些研究取得了丰硕的成果。
FACTS(Flexible AC Transmission System)[1]的概念诞生于20世纪80年代末,其可调节电力系统的潮流分布,从而使电力系统安全、可靠、经济和优质的运行。FACTS的主要元件包括UPFC、可控硅串联补偿器、可控移相器和静止无功发生器等。由于UPFC具有FACTS的多种功能,所以对计及UPFC的无功优化的研究可通过电力系统潮流、电压的控制以及对电力系统暂态稳定性的改善,达到电力系统的潮流最优,提高电网的安全性与经济性,以实现电力系统无功优化水平的进一步提高。所以对计及UPFC的无功优化研究具有重要意义。
1计及UPFC的无功优化模型
1.1 UPFC的数学模型
目前国内外对含UPFC的无功优化研究还较为欠缺,已经提出的考虑UPFC作用的模型有阻抗模型、节点注入功率模型、电压源模型[2]等。在分析文献[3~6]的基础上,将UPFC的可控参数作为控制变量,以系统的有功网损最小为目标,建立含UPFC的无功优化模型。本文采用UPFC的节点注入功率模型,此模型将UPFC对潮流的影响转移到其所在线路的i,j节点上,以达到在不修改原有节点导纳矩阵的情况下嵌入无功优化模型。
UPFC通常表示为一个串联电压源和一个并联电流源的组合,若在线路i-j的节点i侧加入UPFC装置,其等效电路图与等效注入功率模型分别如图1和图2所示。
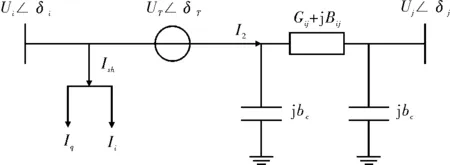
图1 UPFC的等效电路图
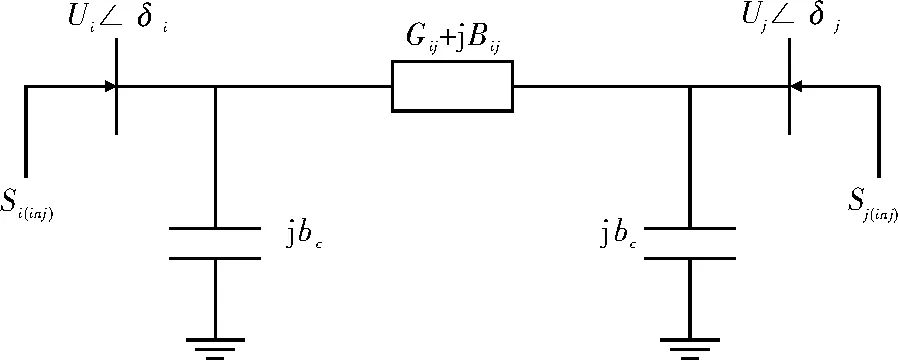
图2 UPFC的节点等效注入功率模型
经推导计算,可得到节点i,j两侧的等效注入功率的直角坐标形式为
Pi(U)=-Gij(ejeT+fjfT)+Bij(fjeT+ejfT)+2(Gij+bc/2)(eieT+fifT)
(1)
(2)
Pj(U)=-Gij(ejeT+fjfT)-Bij(fjeT-ejfT)
(3)
Qj(U)=Gij(ejfT-fjeT)-Bij(ejeT+fjfT)
(4)
其中,e和f分别为节电电压的实部和虚部;eT,fT分别为串联电压源的实部和虚部,即eT=UTcos(δT)、fT=UTsin(δT),Gij、Bij和bc分别为线路i-j的电导、电纳和对地电纳。

对于节点i
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
对于节点j
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
1.2 计及 UPFC的无功优化模型
1.2.1目标函数
本文从经济性的角度出发,以有功网损最小为目标,其目标函数[7-8]如下
(21)
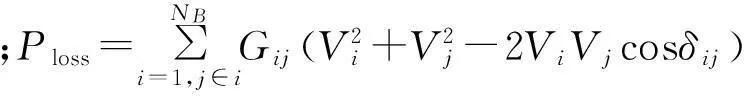
1.2.2等式约束
等式约束是指有功功率与无功功率保持平衡的条件,即功率平衡方程
(22)
(23)
式中,Pi,Qi分别为给定的节点i的有功和无功;Bij为节点i,j之间的电纳值;N0为除平衡节点外的总节点数。
未装置UPFC线路的等式约束为以上潮流公式,装置UPFC线路i-j的等式约束为原有潮流方程增加UPFC的等效注入功率,即i节点处增加Pi(U),Qi(U),j节点处增加Pj(U),Qj(U)。
1.2.3不等式约束
控制变量约束
(24)
式中,Ng、NT和NC分别为可调发电机的节点数、可调变压器的节点数和无功补偿装置的节点数;Vgi、Ti和Qci分别为发电机的机端电压、可调变压器变比和无功补偿装置容量。
计及UPFC后,考虑UPFC的控制变量的约束条件为
(25)
其中,UTmax、UTmin、Iqmax、Iqmin分别为UPFC串联电压源的幅值UT和并联电流源无功分量Iq的上下限。
2计及UPFC电力系统无功优化实现
2.1 粒子群算法
粒子群算法(ParticleSwarmOptimization)由Eberhart和Kennedy两位学者于1955年提出。其将问题的搜索空间比作是鸟群的飞行空间,将每只鸟抽象地看成一个无质量无体积的粒子,表示问题的一个可行解,粒子的好坏由一个事先设定的适应度函数来确定。每个粒子将在可行解空间中运动,并由一个速度变量决定其方向和距离。通常粒子将追随当前的最优粒子,并经过逐代搜索最后得到最优解。在每一代中,粒子将跟踪两个极值,一个是粒子本身迄今为止找到的最优解,即个体极值;另一个是整个群体迄今为止找到的最优解,即全局极值。在每次迭代中,第i个粒子第d维速度更新公式为
vid(t+1)=wvid(t)+c1r1(pid(t)-xid(t))+c2r2(pgd(t)-xid(t))
(26)
位置更新公式为
xid(t+1)=xid(t)+vid(t+1)
(27)
2.2 电力系统无功优化的实现
粒子群算法[9]的最终目的是获得目标函数值处于最优时粒子的位置矢量,即X的各位控制变量。在计及UPFC的无功优化问题中,即由发电机机端电压、可调变压器变比、无功补偿装置投切容量以及UPFC设置的控制变量所组成的矢量
X=[U1;UNG,T1;TNT,C1;CNC,UT1,δT1,Iq1;UTNu,δTNu,IqNu]
其中,NG、NT、NC、NU分别为发电机节点总数、变压器总台数、并联电容补偿点总数及UPFC设置台数。
具体步骤如下:
(1)初始化群种,设定种群的数目为N、维数为D、最大迭代次数k、最大速度v等,且在满足解空间的约束条件下,以随机的方式给出每个粒子的初始位置与速度。
(2)根据适应度函数计算出各个粒子的适应度值,此适应度值作为判断每个粒子位置好坏的标准。
(3)对每个粒子的适应度进行评价,如若第i个粒子的第t次适应度的评价值优于其前(t-1)次适应度的评价值,则将粒子当前的位置设置为最好位置Pbest。
(4)对整体粒子群进行适应度值评价,若第i个粒子的第t次适应度评价值优于其他粒子的适应度值,并且优于整个粒子群历史最好位置的评价,则将该粒子当前的位置设置为整体最好位置Gbest。
(5)根据式(26)更新每个粒子的速度;根据式(27)更新每个粒子的位置。
(6)判断其是否达到最大迭代次数或者终止条件,若达到则输出结果;若未达到返回步骤(2)继续执行,直到达到最大迭代次数为止。
3算例分析与结论
本文使用Matlab进行无功优化仿真计算,以IEEE30节点系统为测试算例。该系统包括6台发电机、4台变压器和2个无功补偿设备。UPFC元件安装在由模态分析技术确定的关键路线4-6靠近节点4处,UPFC的控制参数的取值范围见表1。发电机机端电压的变化范围分别为1.10~0.95p.u.(标幺值,系统基准为100MVA),可调变压器的变比范围为0.90~1.10p.u.,调节步长为1.25%(假设有16个分接头,即17档),并联电容器的调节范围为0~0.50p.u,调节步长为0.05p.u.。系统中,除平衡节点外,在优化前,其它节点电压幅值的初始值均为1.00p.u.,系统所有节点的初始相角均为0.0rad。节点1作为系统的平衡节点,电压幅值为1.06p.u.,相角为0.0rad。
在基于以上初始条件下,对系统采用牛顿——拉夫逊法进行潮流计算[10-11],求得系统的未计及UPFC的初始有功网络损耗为0.059 9p.u.。本文采用的粒子群算法种群大小为30,最大迭代次数为30。
表2是对单独执行粒子群算法,单独计及UPFC的影响及计及UPFC的粒子群算法进行仿真的结果,从有功网损角度看,较初始条件下所得的有功网损0.059 9p.u.粒子群算法有功网损减少了14%,计及UPFC的无功优化减少了10.9%,基于粒子群算法的计及UPFC的无功优化其减少了16.8%。这些结果说明粒子群算法,UPFC设备都对降低电网有功网损有优化的作用。
图3分别为无功优化粒子群算法计及UPFC及未计及UPFC的电力系统中的无功优化结果。结果显示,计及UPFC后,算法达到最优的迭代次数降低,说明UPFC有助于提高算法的收敛性能,并且其有功网损较未计及UFPFC的优化系统降低了4%,说明UPFC能够对降低系统的有功网损起到一定效果。

表1 UPFC控制参数的取值范围

表2 优化结果比较

图3 基于粒子群算法计及UPFC无功优化结果
通过对IEEE30节点算例的计算分析表明,基于粒子群算法的计及UPFC的电力系统无功优化方法可以作为一种新途径用于求解电力系统无功优化问题,值得进一步探索和研究。
参考文献
[1]GeSY,ChungTS.OptimalactivepowerflowincorporatingpowerflowcontrolneedsinflexibleACtransmissionsystems[J].IEEETransactionsonPowerSystems,1999,14(2):738-744.
[2]周玲,王宽,钱科军,等.计及UPFC的电力系统无功优化[J].中国电机工程学报,2008,37(5):37-41.
[3]刘光时.计及统一潮流控制器的电力系统无功优化研究[D].重庆:重庆大学,2012.
[4]VenkateshB,GeorgeMK.FuzzyOPFincorporatingUPFC[J].IEEProceedings-Generation,TransmissionanDistribution,2014,151(5):625-629.
[5]WanliangFang,NganHW.Arobustloadflowtechniqueforuseinpowersystemswithunifiedpowerflowcontrollers[J].ElectronicPowerSystemsResearch,2000,53(11):181-186.
[6]黄若霖.内点法在计及UPFC无功/电压优化中的应用[J].继电器,2008,36(3):15-18.
[7]许文超,郭伟.电力系统无功优化的模型及算法综述[J].电力系统自动化学报,2003,15(1):100-104.
[8]张勇军,任震,李邦峰.电力系统无功优化调度研究综述[J].电网技术,2005,29(2):51-54.
[9]袁晓辉,王乘,张勇传,等.粒子群优化算法在电力系统中的应用[J].电网技术,2004,28(19):14-19.
[10]陈珩.电力系统稳态分析[M].2版.北京:中国电力出版社,1995.
[11]何仰赞,温增银,汪馥英,等.电力系统分析[M].武汉:华中理工大学出版社,1993.

欢 迎 刊 登 广 告
请访问:www.dianzikeji.orgE-mail:dzkj@mail.xidian.edu.cn
联系电话:029-88202440 传真:029-88202440


