三目标柯西粒子群算法的电力系统无功优化
三目标柯西粒子群算法的电力系统无功优化
马立新,栾健,王继银
(上海理工大学 电气工程系,上海200093)
摘要通过建立有功网损最小、电压偏差最小和静态稳定电压裕度最大的三目标无功优化模型。提出柯西粒子群算法,并针对IEEE14节点系统进行三目标电力系统无功优化。当种群多样性较差时,通过对交叉的粒子进行柯西变异从而扩大搜索空间,提高种群多样性,防止出现过早的收敛,进而避免了算法陷入局部最优解的问题,同时也提高了收敛速度。通过数据测试和比较柯西粒子群算法在收敛速度、精度、全局搜索能力上均优于常规差分进化算法和常规粒子群算法。其结果验证了该模型和算法的有效性,为电力系统安全经济运行提供了参考。
关键词电力系统无功优化;差分进化算法;粒子群算法;静态稳定电压裕度
收稿日期:2014-11-07
基金项目:国家自然科学基金资助项目(61205076)
作者简介:马立新(1961—),男,博士,教授。研究方向:电力系统分析与优化运行,智能电网与智能科学,电气设备状态监测与诊断方法等。E-mail:luckmath@126.com
doi:10.16180/j.cnki.issn1007-7820.2015.09.011
中图分类号TM744
Three-objective Cauchy Particle Swarm Optimization for Reactive Power Optimization
MA Lixin,LUAN Jian,WANG Jiyin
(Department of Electrical Engineering,University of Shanghai for Science & Technology,Shanghai 200093,China)
AbstractThis paper establishes a three-objective hybrid algorithm,which takes into account of loss minimization,voltage level best target and maximum static voltage stability margin.The Cauchy particle swarm optimization (CPSO) algorithm is proposed and applied to IEEE-14 node system for three-objective reactive power optimization.Cauchy particle swarm optimization (CPSO) is basic particle swarm algorithm to join the Cauchy distribution,for each generation of the particle’s velocity,position,and Cauchy mutation adaptive value,thereby increasing the diversity of population.When the population diversity is very poor,Cauchy mutation is performed by particles to cross in order to expand the search space,improve the population diversity and avoid premature convergence,thereby avoiding the problem of algorithm trapped in local optimal solution with improved convergence speed.By testing data and comparing rate of convergence,accuracy and global searching ability of the new algorithm,CPSO algorithm is found to be superior to the conventional DE algorithm and PSO algorithm.The results show the validity of the proposed model and algorithm,which has important theoretical guiding significance for the security and economic operation of power system.
Keywordspower system reactive power optimization;differential evolution algorithm;particle swarm optimization algorithm;static voltage stability margin
电力系统无功优化是提高电网高效运行和节能的关键。电力系统无功优化是指在给定电网机构参数及用电负荷,满足各节点功率平衡及各设备安全运行的条件下,保证电压质量,通过调整无功补偿装置,使电力系统中的无功分布达到最佳状态,从而起到减少有功网损,改善电压质量。目前,大多数无功优化只考虑有功网损及电压偏差两个方面。然而,随着现代化的发展,电力网会出现超负荷运行状态,导致了静态电压裕度偏低,从而导致故障发生,造成严重的损失情况。
粒子群(PSO)算法是以无体积无质量的粒子为个体,规定每个粒子个体的社会行为规则,通过种群间的协调,实现对问题最优解的搜索[1-2]。该算法简单、计算方便、求解速度快,但存在着陷入局部最优解等问题。
基于粒子群算法的上述缺点,提出了柯西粒子群算法,并将柯西粒子群算法进行三目标电力系统无功优化。
1三目标无功优化数学模型
1.1 目标函数
(1)电网有功网损Ploss。考虑经济因素,有功网损应达到最小。目标函数表达式如下
(1)
式中,Nl为系统网络支路总数;Gk为支路k的电导;i、j分别为支路k两端节点号;Ui、Uj分别为节点i、j的电压值;δi、δj分别为节点i和j的电压相角。
(2)电压偏差dv。考虑稳定因素,电压偏差应达到在满足条件范围内最小。目标函数表达式如下
(2)

(3)增大静态电压裕度VSM。考虑安全性因素,达到电压裕度应达到在满足条件范围内最大。目标函数如下
(3)
式中,δmin为收敛潮流雅可比矩阵的最小奇异值。
1.2 约束条件
(1)功率约束。有功功率与无功功率保持平衡的约束条件
(4)
式中,Pi为有功功率;Qi为无功功率。
(2)变量约束。控制变量
(5)
式中,QG为发电机的端电压;T为可调变压器的变比;QC为电容补偿功率。状态变量
(6)
式中,UL为负荷节点电压;UG为发电机无功出力。
1.3 目标函数转换
考虑有功网损、电压偏差及静态电压裕度3方面的因素,由于各因素的量纲不同,因此不能将其进行直接叠加。首先,进行去量纲化,公式为
(7)
式中,P0为初始潮流有功损耗;d0为初始电压偏移。
将3个不同量纲的因子进行归一化,并赋予因子权值,将式(1)~式(3)的3目标优化模型转化为单一目标优化模型
(8)
式中,ω1为有功网损;ω2为电压偏差和ω3为静态电压裕度的权重,且ω1+ω2+ω3=1。
2柯西粒子群(CPSO)算法
2.1 基本的粒子群算法( PSO)
粒子群算法的原理是将分散在搜索空间里的每个粒子赋予一定的初始速度,并根据个体和群体在飞行过程中,不断更新速度及更新位置,最终根据目标函数,计算出最优值的过程[3-4]。
PSO算法中粒子速度和粒子位置的更新公式
vid(k+1)=ωvid(k)+c1r1(pid(k)-xid(k))+c2r2(pgd(k)-xid(k))
(9)
xid(k+1)=xid(k)+vid(k+1)
(10)
式中,vid(k)为粒子i在第k次迭代中第d维的速度;xid(k)为粒子i在第k次迭代第d维的位置;ω为惯性权重;c1、c2为称学习因子;pid(k)为整个粒子群在第k次迭代第d维的个体极值点的位置;pgd(k)为整个粒子群在第k次迭代第d维的全局极值点的位置;r1、r2为[0,1]区间独立的均匀分布的随机数。
2.2 柯西粒子群( CPSO)算法
标准粒子群算法能够快速计算出优化问题,却在处理问题中易陷入局部最优。其中的原因是:粒子能够快速计算出局部最优的gbest一点,gbest在一段时间内并未变化。随着粒子的不断运动,群体的多样性越来越小,粒子之间的差异性越来越小,从而产生了局部最优解的问题。为解决此问题应将期望全局最优粒子gbest能够跳出局部最优,并带动其他粒子逃离[5-8]。
群体平均速度公式
(11)
式中,Vij是第i个粒子的第j维速度分量;Popsize是群体大小。
自适应的柯西变异:对于第i个粒子Xi=(Xi1,Xi2,…,Xin),对该粒子的柯西变异是根据如下公式
(12)
式中,j=1,2,…,n,c是由t=1的柯西分布函数产生的随机数,xij在[xmin,xmax]范围内。
2.3 算法步骤
步骤1随机生成一个种群,初始化每个粒子的速度和位置,对种群中参数进行赋值。
步骤2迭代计数器t=0。
步骤3按照式(9)~式(10)对群体中粒子进行速度、位置更新。
步骤4按照式(11)~式(12)对群体中粒子进行选择操作、变异操作。
步骤5将每个粒子的适应值与上一个适应值进行比较,得出较好的作为当前最优位置Pid。
步骤6将步骤4中得出较好的当前位置与群体全局最好的位置进行比较,得出较好的作为全局的最优位置Pgd。
步骤7选出群体中适应度最好的粒子,作为柯西粒子群下一代进化的粒子。
步骤8判断是否满足终止条件,若满足则终止;否则t增加1,转向步骤3继续执行。
3算例及结果分析
3.1 算例
为了验证算法的可行性和有效性,对IEEE-14节点测试系统进行了无功优化计算,并将结果与基本PSO算法、基本DE算法等在同等迭代次数等条件下进行了比较以IEEE-14节点系统为例进行计算分析,该系统共有20条支路、2台发电机,3台有载调压变压器。节点2、3、6、8为PV节点;节点9为并联补偿电容器节点。负荷节点都属于PQ节点。PQ、PV节点电压的范围为[0.95,1.10],有载调压器变比范围为[0.90,1.10],调节步长为1.25%,即17档,并联电容器的调节范围为[0.00,0.50],步长为0.05。系统的基准容量取100MVA。
3.2 优化结果分析
差分进化算法、粒子群算法及柯西粒子群算法用于IEEE14节点电力系统无功优化得出表1,从表1可得出CPSO算法的电力系统无功优化的有功网损为0.087kW,比差分进化算法与粒子群算法分别节省5.776%和2.247%。并且从另外两个方面考虑,电压偏差和稳态电压裕度也具有明显的优势。充显示了本文算法的有效性,能够得到更好地最优解,全局寻优能力较高。

表1 IEEE14节点系统各算法比较
由算法迭代图1可得,3种算法的电压幅度均在5%之间,而CPSO算法的幅度明显好于DE和PSO算法。
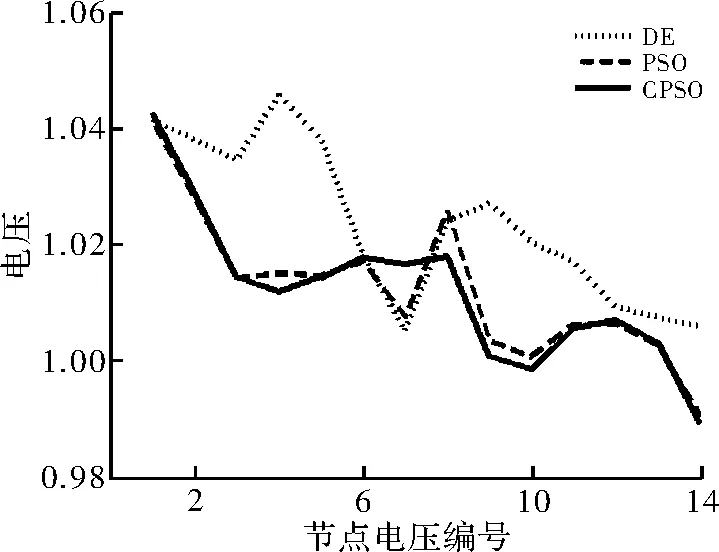
图1 IEEE-14节点系统电压分布
由算法迭代图2得出有功网损CPSO算法为0.087kW,该算法小于PSO算法和DE算法的有功网损。而有功网损越小,说明经济性越好。

图2 IEEE-14节点系统有功网损
由算法迭代图3得出CPSO算法电压偏差为0.032kV,该算法小于DE算法和PSO算法电压偏差。而电压偏差越小,说明电网运行越安全。

图3 IEEE-14节点系统电压偏差
由算法迭代图4得出CPSO算法静态电压裕度为1.884 8,该算法大于DE算法和PSO算法的静态电压裕度,而静态电压裕度越大表明电力系统中越稳定。
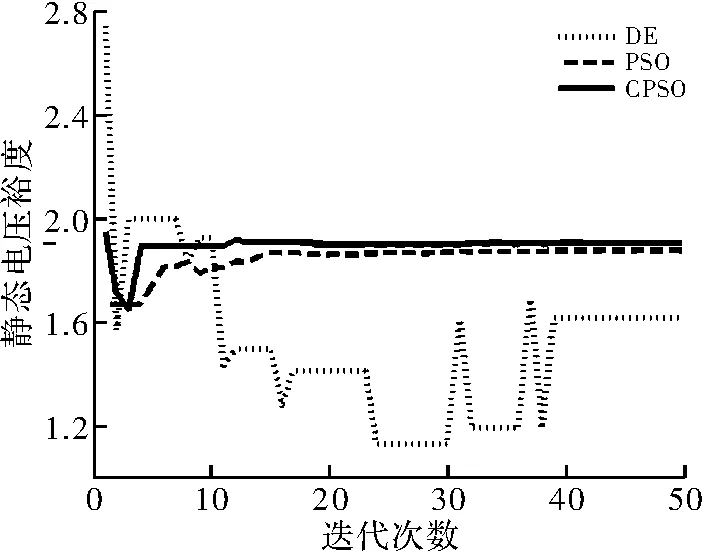
图4 IEEE-14节点系统静态电压裕度
通过图2~图4综合比较,验证了柯西粒子群(CPSO)算法在进行电力系统无功优化过程中,收敛速度和全局搜索能力方面都得到了提高。
4结束语
本文从有功网损、电压偏差及稳态电压裕度3个方面综合考虑,进行了电力系统无功优化。并针对粒子群解决电力系统无功优化中存在着收敛速度慢、易陷入局部最优化等问题,提出了柯西粒子群算法。该算法提高了PSO算法的优化性能,克服了PSO算法的局部最优化问题及后期收敛速度慢等缺点。并将算法应用于IEEE14节点系统进行3目标电力系统无功优化,分析结果验证了模型和算法的有效性,其在实现电力系统无功优化经济运行的同时增强了电网电压的稳定性。
参考文献
[1]马立新,屈娜娜,单冠华,等.电力系统无功优化的柯西粒子群算法[J].控制工程,2011,18(5):758-761.
[2]马立新,孙进,单冠华,等.多目标差分进化算法 的电力系统无功优化[J].控制工程,2013,20(5):1671-7848.
[3]宋通,庄毅,郭云.基于大向搜索差分进化的多目标优化算法[J].电子科技,2012,25(5):119-122.
[4]邱威,张建华,刘念.自适应多目标差分进化算 法在计及电压稳定性的无功优化中的应用[J].电网技术,2011,35(8):81-87.
[5]刘群英,刘俊勇,刘起方.节点势能架构下的电 压脆弱性评估[J].中国电机工程学报,2008,28(25):30-37.
[6]李鑫滨,朱庆军.一种改进粒子群优化算法在 多目标无功优化中的应用[J].电工技术学报,2010,25(7):137-143.
[7]张聪誉,陈民铀,罗辞勇,等.基于多目标粒子群 算法的电力系统无功优化[J].电力系统保护与控制,2010,38(20):153-158.
[8]肖力.一种改进的遗传算法在无功优化中的 应用[J].计算机仿真,2010(8):278-281.



