FPGA实现基于施密特正交化的自适应算法
FPGA实现基于施密特正交化的自适应算法
包志强,贾富伟,朱少彬
(西安邮电大学 通信与信息工程学院,陕西 西安710121)
摘要在自适应波束形成算法理论基础上,将修正施密特正交化算法运用在基于三角分解的样本矩阵求逆算法中,提出了基于修正施密特正交化算法的三角分解矩阵求逆算法,并给出了具体的可编程门阵列硬件实现结构。该硬件结构的实现采用了坐标旋转数字计算机代替该算法中的除法运算,有效地节约了硬件资源消耗和结构时延。通过硬件仿真对计算结果进行分析研究,实验证明该硬件结构不仅有良好的数值稳定性,能对干扰有效抑制,且硬件资源消耗少,高度模块化。
关键词FPGA;修正施密特正交化;三角分解;自适应波束形成
收稿日期:2015-03-02
基金项目:国家自然科学基金资助项目(61271276);陕西省自然科学基金资助项目(2012JQ8011);陕西省教育厅专项科研计划项目(14JK1681)
作者简介:包志强(1978—),男,博士,副教授。研究方向:阵列信号处理。E-mail:baozhiqiang@xupt.edu.cn。贾富伟(1988—),男,硕士研究生。研究方向:现代数字信号处理。
doi:10.16180/j.cnki.issn1007-7820.2015.09.001
中图分类号TN97;O151.21
QRD-SMI Algorithm Based on MGS Algorithm and its FPGA Implementation
BAO Zhiqiang,JIA Fuwei,ZHU Shaobin
(School of Communication and Information Engineering,Xi’an University of Posts and
Telecommunications,Xi’an 710121,China)
AbstractBased on the theoretical analysis of adaptive beamforming algorithm,the modified Gram Schmidt orthogonal algorithm (MGS) is used in the algorithm based on the QR decomposition of inversion sample matrix (QRD-SMI) to propose the QRD-SMI algorithm based on the MGS algorithm with specific programmable gate array (FPGA) implementation structure given:multiplexing QR decomposition array (MQRD-IMGS) based MGS.The FPGA implementation structure uses coordinate rotation digital computer (CORDIC) to replace the division operational in MGS,effectively saving hardware resource consumption and the structure time delay.Hardware simulation shows that the highly modular MQRD-IMGS maintains numerical stability with good suppression of the interfering signals and small hardware resource consumption.
KeywordsFPGA;modified Gram Schmidt orthogonal algorithm;QR decomposition;adaptive beamforming
QR分解的采样矩阵求逆算法(QR Decomposition of Inversion Sample Matrix,QRD-SMI)因为良好的数值特性和易于通过构建脉动阵并行实现成为研究热点[1-2]。QRD-SMI算法需要对接收端数据进行QR分解。常用QR分解法分为3大类:修正的施密特正交算法(Modified Gram Schmidt orthogonal algorithm,MGS)[3-5]、Givens 旋转变换法(Givens Rotation,GR)[6-7]和Household 变换法[8]。同另外两种方法相比,GR算法更容易通过构建含有坐标旋转数字计算机(Coordinate Rotation Digital Computer,CORDIC)模块[9-10]的三角脉动阵列结构(Triangular Systolic Array structrue,TSA)[11-13]来实现矩阵的QR分解,所以工程应用中也更多采用GR算法。但是一些研究表明改良后的MGS算法(QR Decomposition-Modified Gramschmidt Orthogonal Algorithm,QRD-MGS)在数值分析上同GR算法有着相同的性能。目前关于QRD-MGS算法及其硬件结构的研究更多的是关注QRD-MGS算法在多输入多输出(Multiple-Input Multiple-Output,MIMO)信道中对信道矩阵求逆的运用,其相应的硬件结构并不适用于直接对接收端天线的数据矩阵进行处理[14-15];关于将QRD-MGS算法与脉动阵相结合,构建能实时对接收端数据矩阵进行QR分解的FPGA结构,并探讨其在自适应干扰抑制上运用的研究较少。
本文创新点是将QRD-MGS算法与脉动阵相结合,设计出一种基于SMI算法的自适应权值计算的FPGA结构,并对算法对应的硬件结构进行了优化,对复数乘法器进行了时分复用,调用Xilinx CORDIC IP核[16-17]和DDS IP核[18-19]避免了乘方和开方运算,获得了时延上的性能提升,且减少了FPGA的资源消耗。能实时对数据矩阵进行QR分解,并对基于QR分解的自适应波束形成[20-22]的现实应用具有良好的指导意义和实用价值。芯片选为Xilinx virtex-5 xc5vfx70t。在不同通信环境下仿真分析了该设计的性能。分析表明该设计具有良好的运算性能,且当接收端天线数目增加时,扩展性良好。
1自适应波束形成
自适应波束形成技术的主要目的是使阵列方向图在期望的方向上形成主瓣,并使天线的零点对准干扰方向,达到空域滤波的目的。基本理论是:基于某个标准和自适应算法,对输出端信号加权求和,使得期望信号的输出功率最大,从而得到其导向位置即给出波达方向估计。
接下来建立信号处理模型。假设阵列为等距线阵,阵元个数为M,间距为d,信源个数为D(M>D),波达角分别为(θ1,θ2,…,θD)。假设第一个阵元为参考点,信源的复包络分别为S1(t),S2(t),…,SD(t),所以在第m个阵元上第k次快拍的采样值如下式
(1)
式中,nm(k)表示第k个阵元上的零均值高斯白噪声。由此得到整个阵列第k次快拍的接收信号为
(2)

接收端阵列天线的输出信号为
Y(k)=WHX(k)
(3)
这里W=[w1,w2,…,wM]T是权矢量。
通过调整自适应天线的权矢量可以使自适应波束形成的性能达到最佳。使性能达到最佳状态的标准有多种,如最大信干噪比准则,最小均方误差准则,线性约束最小方差准则等。本文则是选择线性约束最小方差准则进行研究。
线性约束最小方差准则可描述为
(4)
这里F为任意非零常数;Rxx=E{X(k)XH(k)}为接受端阵列输入信号的自相关矩阵;θd为期望信号的波达角,即在满足WHa(θd)=1的前提下,使得输出信号Y(k)和期望信号d(k)之间的均方误差最小的权矢量即为最优。解式(4),得到最优权矢量为
(5)
2QRD-IMGS算法
QRD-MGS算法是一种由若干个向量a1,a2,…,an构造相互正交,且范数为1的向量q1,q2,…,qn的方法。对于复数域的一个m×n矩阵X,X的秩Rank(X)=n,X=[x1,x2,…,xn]。xi(i=1,2,…,n)标识矩阵X的列向量。对X用经典的施密特正交算法进行QR分解过程如下:
(1)首先对x1做标准正交化得到向量Q1
(6)
(2)接着减去x2中与x1平行的分量,再对差分向量标准正交化,正交化的结果作为Q2
(7)
(3)依次类推,对于Qk(2≤k≤n)则有
(8)
对QRD-CGS算法稍加修改,将按列求解上三角阵元素改为按行求解上三角阵元素,就得到了QRD-MGS算法。
若将该算法直接应用在自适应波束形成算法中,需要先计算接收信号的自相关矩阵
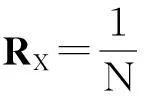
然后对RX进行QR分解,即无法直接处理接收数据矩阵X。本文对该算法修改后,给出可以直接处理接收数据矩阵的QRD-IMGS算法,实时接收新的数据,更新一次上三角阵,直至接受全部采样点,求得最后的上三角阵。
对接收端数据矩阵X采用QRD-IMGS算法进行GR分解的流程如下,其中上三角阵R的初始值为零矩阵

(9)
酉阵Q的第一列qi1
(10)
(2)R′第一行上的非对角线元素由式(8)可得
(11)
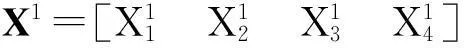
(12)
(3)令X=X1,同理重复(1)和(2)可以求得上三角阵剩余的元素,由此得到新的上三角阵R″,令R=R″。
(4)返回(1)再次接收新数据,重复上述步骤(2)~步骤(4),更新一次上三角阵,直至接受完全部采样点,求得最后的上三角阵。
3硬件结构设计
将QRD-IMGS算法中的通过除法器求解Q1改为使用Cordic算法来求解,并对内部单元乘法器进行时分复用,可以减少硬件资源消耗,具体如下:
(1)边界单元接收当前列的5个元素Xj=[x1j,x2j,x3j,x4j,x5j]T
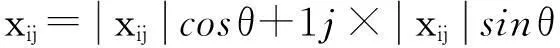
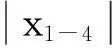
qij=sin(φij)cos(θij)+1j×sin(φij)sin(θij)
(13)
(3)修改后的边界单元依次输出:q1j,q2j,…,q5j这样内部单元就可对同一乘法器,分时调用来求得上三角阵的非对角元素,节约了乘法器资源。
具体硬件结构图如图1和图2所示,图2中的IF模块判断是否接受完qij和是否完成了Qj和Xj+1的内积运算,rij的求解。Cordic核得到rij和θij,避免了乘方和开方运算,将求解式转化为三角函数关系运用DDS核求解避免了除法运算。
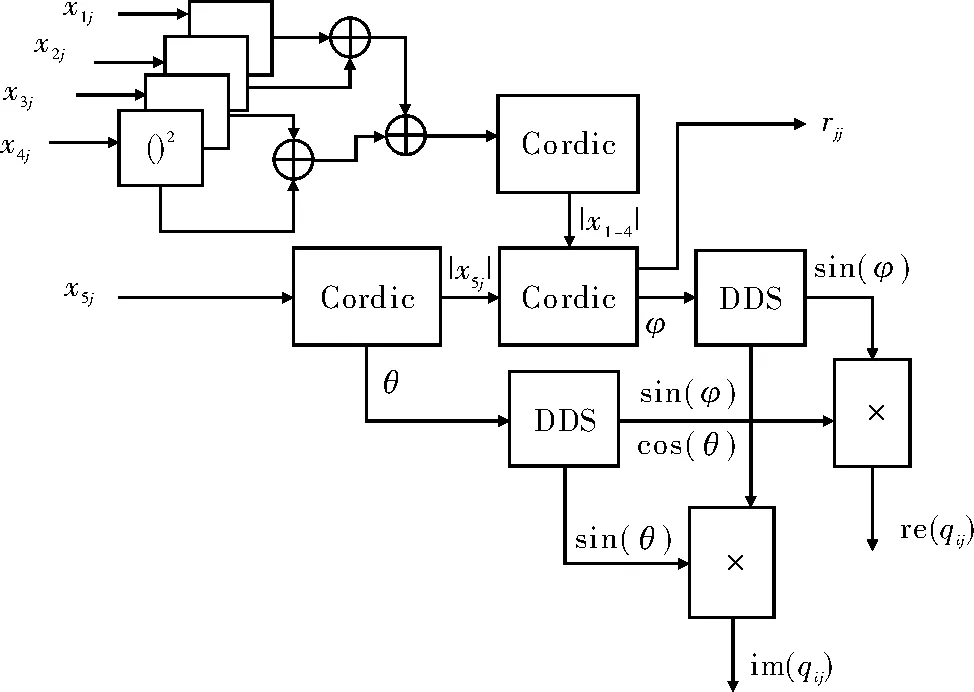
图1 边界单元DP的硬件结构
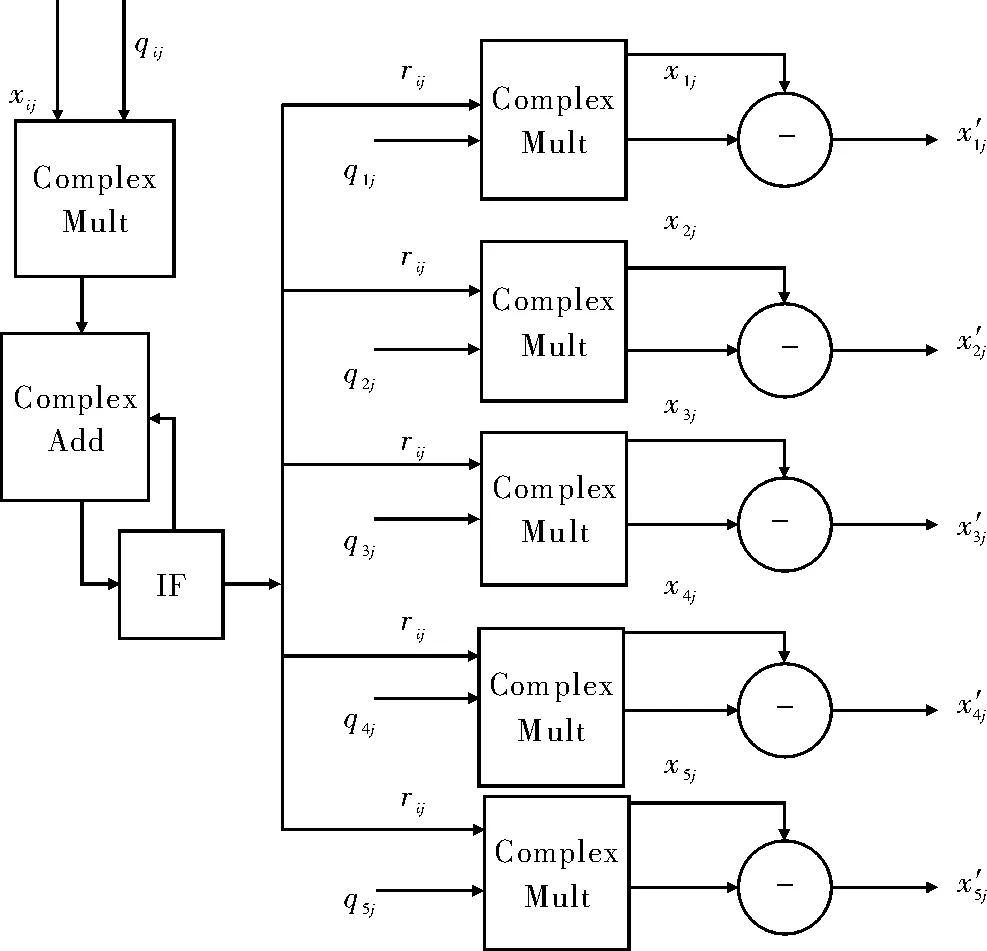
图2 内部单元TP的硬件结构
4仿真和硬件实施结果
在Xilinx的ISE软件中,采用VHDL语言进行算法编写,芯片选择Xilinx的virtex-5xc5vfx70t,并在ISE软件下进行仿真验证,最后将输出结果返回Matlab,同浮点计算的输出结果进行比较。仿真时,使用Matlab-M文件编程模拟信号源,接收端数据量化格式为二进制补码,量化宽度为16位,包括符号位、整数位(7位)和小数位(8位)。中间数据C、S和上三角阵被截位成24位。图3是XilinxISE计算的上三角阵结果。

图3 ISE 计算结果
最后将Matlab的浮点计算结果进行量化后的上三角阵R(量化位为1位符号位,11位整数位,12位小数位)与图3中的结果做误差分析。
为了进一步研究该结构的硬件性能,本文仿真设置了两种实验条件。
实验条件:(1)通过Matalb产生100组功率为1的高斯随机数据阵(4行32列),在保证整数位宽相同的前提下,将这些数据阵量化成不同小数位宽的定点数,导入ISE中,进行QR分解;按照下式将ISE的计算结果同Matlab的计算结果进行误差计算,最后得到该算法的平均误差百分比

(14)
(15)
其中,Rmatij表示Matlab浮点计算的上三角阵Rmat第i行第j列的元素;Rij表示ISE定点计算的上三角阵R第i行第j列的元素。
图4和图5显示了不同小数位宽下,该硬件结构计算的平均误差和误差百分比。
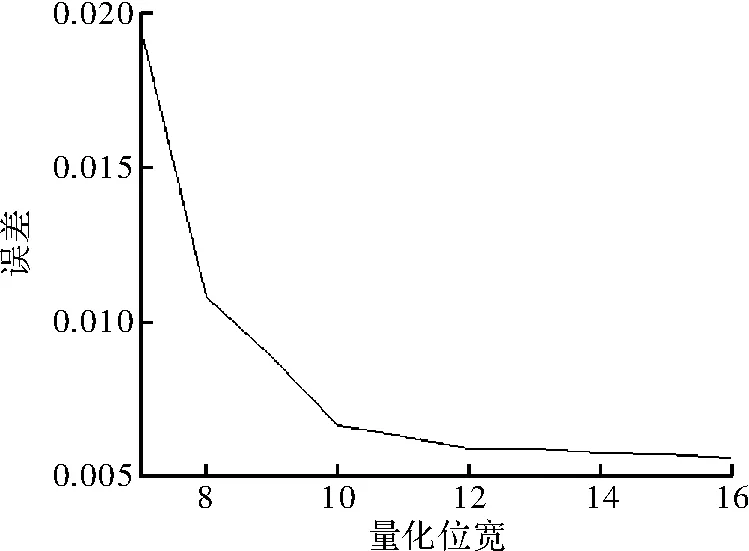
图4 量化位宽与误差的关系

图5 量化位宽与误差百分比的关系
当量化的小数位宽>13位时,计算误差和误差百分比趋于稳定。
(2)接下来固定小数位宽为15位时,验证采样点数与计算误差的关系。取10 000次采样点的数据,在Matlab中做浮点计算得到上三角矩阵作为真值,用来与硬件实现的数据处理结果进行对比,得到采样点数与计算误差的关系如图6和图7所示。

图6 采样点数与误差的关系

图7 采样点数与误差百分比的关系
随着采样点数的增加,两者之间的误差随之减小,当采样点数>1 500点之后,差值趋于稳定,采样点数的增加对该结构的计算性能影响不再明显。
接下来研究采样点数与方向图的关系,假设在当前的通信环境中期望信号的波达角度为50°,信噪比为20dB,存在一个70dB的窄带强干扰,波达角度为-60dB,以此为模型,在Matlab中产生阵列天线的接收端数据源,量化后导入ISE中进行QR分解。在上述通信环境下,文中QRD-IMGS结构算出的上三角阵返回到Matlab,计算权值与方向图8给出了在采样点分别为500,1 000,1 500,2 000,5 000时的方向图,当采样点>2 000时,两种采样点下的方向图已基本重合,在干扰方向形成零陷,在期望方向上θ=50°,获得了最大增益值,干扰得到了有效抑制。

图8 不同采样点下的方向图
5结束语
针对阵元数较多时,QRD-IMGS结构硬件资源消耗过大的缺点,提出了修正QRD-IMGS结构。通过CORDICIP核和DDSIP核的调用,避免了除法器的使用和乘法器在硬件中的分时复用,有效减少了XtremeDSPSlices的消耗。经过仿真,当输入端量化为16位时,采样点数为1 500点时,计算精度能达到10-4,2 000次采样点以后趋于稳定。当采样点数2 000时,修正QRD-IMGS的自适应波束形成系统能得到有效地方向图,并在干扰方向形成零陷,继续增加采样点数不能明显改善系统性能。
参考文献
[1]段斌.基于QR分解的卫星导航系统干扰抑制方法与DSP设计[D].西安:西安电子科技大学,2012.
[2]马晓龙,陈贵灿.基于脉动阵列的复数定点QR分解VLSI设计[J].微电子学,2011,41(5):685-689.
[3]RainfieldYYen,HongYuliu,YungChangYin.High-orderapproximationalgorithmusingGram-SchmidtQRtransformationscoupledwithaniterativecorrectionprocessfortrackingfrequencydriftinOFDMsystems[J].EURASIPJournalonWirelessCommunicationsandNetworking,2014(1):1-13.
[4]SalamA,Al-AidarousE.EquivalencebetweenmodifiedsymplecticGram-SchmidtandhouseholderSRalgorithms[J].BITNumericalMathematics,2014,54(1):283-302.
[5]RobertChenhaoChang,ChihHungLin,Kuang-HaoLin,etal.IterativeQRdecompositionarchitectureusingthemodifiedGram-SchmidtalgorithmforMIMOsystems[J].IEEETransactionsonCircuitsandSystems,2010,57(5):1095-1102.
[6]MaltsevA,pestretsovV,MaslennikovR,etal.TriangularsystolicarraywithreducedlatencyforQR-decompositionofcomplexmatrices[C].IslandofKos,Greece:ProceedingofIEEEInternationalSymposiumonCircuitsandSystems,2006:385-388.
[7]ArtyomMGrigopryan.Newmethodofgivensrotationsfortriangularizationofsquarematrices[J].AdvancesinLinearAlgebra&MatrixTheory,2014,4(2):65-78.
[8]李明玉,刘金亭,冯文江,等.自适应数字预失真系统Householder块精确逆QR分解递归最小二乘法[J].应用科学学报,2013,31(4):345-352.
[9]AlexanderSW,PfannE,StewartRW.AnimprovedalgorithmforassessingtheoverallquantizationerrorinFPGAbasedCORDICsystemscomputingavectormagnitude[J].MicroprocessorsandMicrosystems,2006,31(2):87-93.
[10]JavierValls,MartinKuhlmann,KeshabKParhi.EvaluationofCORDICalgorithmsforFPGAdesign[J].TheJournalofVLSISignalProcessing,2002,32(3):207-222.
[11]包志强,丁康利,单洁.基于脉动阵的自适应波束形成算法仿真[J].无线通信技术,2014,23(2):1-5,10.
[12]杜鹤,买培培,苏涛,等.QR_RLS算法的浮点脉动阵结构研究与FPGA实现[J].现代雷达,2011,33(5):26-29,35.
[13]齐海兵.流水线自适应格型联合处理器的FPGA设计[J].微电子学与计算机,2010,27(7):49-52,56.
[14]SightCK,PrasadSH,BalsaraPT.VLSIarchitectureformatrixinvesionusingmodfiedGram-SchmidtbasedQRdecomposition[C].20thInternationalConferenceonVLSIDesign,2007:836-841.
[15]冯地耘,陈立万,王悦善.自适应波束形成与高性能DSP[M].成都:西南交通大学出版社,2007.
[16]孙书龙.基于Cordic算法的AM调制器IP核的研究与实现[J].现代电子技术,2014,37(13):162-163,166.
[17]杨宏,李国辉,刘立新.基于FPGA的Cordic算法的实现[J].西安邮电学院学报,2008,13(1):75-77.
[18]刘马良,朱樟明,郭旭龙,等.一种4路内插Cordic的14位吉赫兹DDSIP核[J].西安电子科技大学学报,2013,43(6):62-66.
[19]万志江.基于FPGA的DDSIP核的研究与设计[J].微电子学与计算机,2013,30(8):98-102.
[20]李荣锋,王永良,万山虎.基于快速逆QR分解的自适应波束形成方法[J].系统工程与电子技术,2002,24(9):27-29,77.
[21]朱少彬,卢光跃,包志强.基于QR分解自适应波束形成算法的FPGA实现[J].无线通信技术,2013,22(4):16-20.
[22]卢光跃,弥寅,包志强,等.基于特征结构的频谱感知算法[J].西安邮电大学学报,2014,15(2):1-12.



