基于向量积的多边形中心的计算方法
基于向量积的多边形中心的计算方法
王红喜
(陕西职业技术学院 计算机系,西安 710100)
摘要:为了确定多边形的中心,将多边形分割为三角形,利用向量的向量积计算各个三角形和多边形的面积,给出计算多边形中心的一种方法,并对具体的数据进行了仿真实验.结果表明算法的正确性和可行性.
关键词:多边形;向量的向量积;中心
中图分类号:O24文献标志码:A
文章编号:1008-5564(2015)03-0042-05
收稿日期:2015-04-30
基金项目:江苏省高校自然科学研究面上项目(14KJB18000);江苏省高等学校大学生创新创业训练计划项目(201410292025Z);常州大学学生课外创新创业基金资助项目(2014-02-A-04)
作者简介:李琳(1994—),女,江苏镇江人,常州大学生物医学工程与健康科学研究院常州市呼吸医学工程重点实验室学生,主要从事生物技术研究.
通讯作者:*邓林红 (1960— ),男,四川夹江人,常州大学生物医学工程与健康科学研究院常州市呼吸医学工程重点实验室教授,博士生导师,教育部 “长江学者奖励计划”特聘教授,主要从事生物力学和呼吸医学工程研究.
An Algorithm Base on the Cross Product of Vectors forDetermining the Center of Polygons
WANG Hong-xi
(Deparment of Computer, Shaanxi Vocational & Technical College, Xi’an 710100, China)
Abstract:An algorithm is provided to determine the center of polygons. In this algorithm, polygons are divided into triangles and areas of every triangle and polygon are calculated by the cross product of vectors. Eventually the specific data are simulated and the results show that the algorithm is correct and feasible.
Key words:polygons; cross product of vectors; center of polygons
计算多边形的中心在生产实践中有着广泛的应用.例如,在材料应用中,对多边形的金属板件或木质板材的余料加工时,为了提高材料利用率,减少废料,确定最大内圆的圆心以及半径是一个常见问题[1-2];在高层建筑物维修中,需要测量建筑物诸如倾斜、弯曲等变形问题.可通过计算建筑物各层中心连线是否在同一直线上确定.计算多边形中心有多种算法,文献[1]给出了一种任意多边形中心的计算方法,但该方法需根据参考点确定圆心的搜索方向,同时步长因子的选取对计算时间有着较大的影响.
本文提出一种针对任意多边形计算中心(寻找最大内圆)的方法,首先将多边形分割为多个互补相交的三角形,然后利用向量的向量积计算各个三角形的面积进而得到多边形的面积,最终确定多边形的质心(中心),克服了文献[1]中计算的缺点.同时为了验证算法的正确性和可行性,利用Matlab软件对具体的算例进行了实验.同时与文献[1]方法计算的结果进行了比较.结果表明,本文方法计算正确且易于实现,具有一定的应用价值.
1数学知识
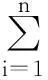
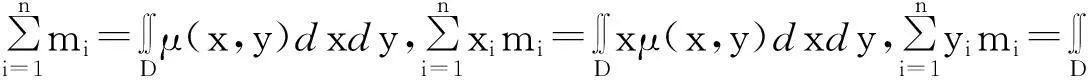
则质心即为中心,其坐标表示为:
(1)
若多边形结构的薄片是均匀的,则密度ρ=μ(x,y)为常数,S为区域D的面积,则质心即为中心,则公式(1)化为:
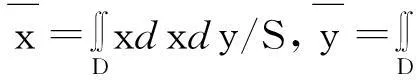
(2)
2算法与数值计算
首先,计算区域D的面积S,讨论以下两种情形:
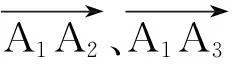
(3)
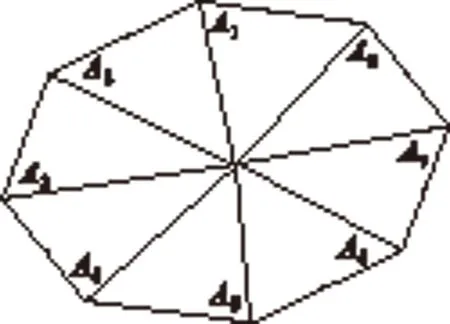
图1 多边形的分割
(b)若多边形为形边数n(n>3),多边形顶点坐标为Ai(xi,yi)(i=1,…,n),此时将多边形分割成互不相交的n个三角形△A1OA2,△A2OA3,…,△An-1OAn,如图1所示(以八边形为例).
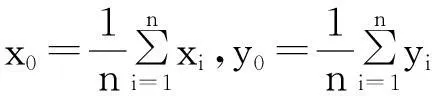
其次,质心(中心)的计算.
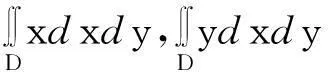
(4)
故质心(中心)的数值计算只需将(4)式的计算结果和S带入(2)式即可.需要说明的是,若多边形为三角形,则(2)式的分子项计算仍需要按(b)中讨论的方法算出,分母项则可按公式(3)计算得到.
以上讨论归结为算法:
Step1.记多边形的顶点个数为n(n≥3);
Step2.Fori=3:n
Ifn=3
①利用公式(3)计算多边形的面积S;
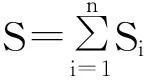
else
转②
End
3算例及比较结果
为验证本算法的正确性和可行性,分别用文献[1]的方法和本文方法对具体的数据进行了实验.设多边形为八边形,其顶点以及坐标为:A1(565.454,528.012)、A2(562.058,528.012)、A3(561.39,521.477)、A4(563.782,518.108)、A5(567.941,517.407)、A6(571.255,519.857)、A7(571.938,523.953)、A8(569.5,527.356).(数据来源:2013全国大学生数学建模乙组C题).采用Matlab软件计算八边形的中心结果如表1.

表1 两种方法的计算结果
对于两组数据A、B,采用误差公式‖A-B‖2,将表一的两组数据带入可得两种方法的误差不超过0.7.两种方法计算的结果较为接近.而文献[1]方法计算需花费几分钟,而本文方法仅仅需要几秒钟即可算出,需说明的是两种方法都是在Matlab软件环境下实现的.文献[1]方法则是AutoLISP环境下实现的,计算时需要对数据先进行处理.由于实际问题需要处理大量的数据,使用Matlab软件更为方便.
4结语
本文给出了一种计算任意多边形的中心(寻找最大内圆)的计算方法,对多边形采用了分割的方法,利用向量的向量积计算分割出图形的面积进而求出多边形的面积,然后就算出多边形的中心.最后需说明的是:本文的方法讨论的是对于多边形形状的构件,假设材料是均匀的.若材料不均匀计算时将多边形各顶点处的密度带入公式(1)即可.本文数学原理清晰,构思巧妙,算法简单且易于实现.同时利用具体的数据对文献[1]的方法和本文方法进行了实验.结果表明本文算法的正确性和可行性,具有一定的应用价值.
[参考文献]
[1]郑梅生,陈宁,宋超.计算任意多边形最大内圆的一种算法[J].机械设计与制造,2003,5 :84-85..
[2]宋继明,宋华松,汪以文.特殊地形条件下杆塔倾斜率的测量方法[J].电网技术,2012,34(12):219-222.
[3]窦长旭,王玉玫.多边形中心点向量的二次插值变形算法[J].计算机工程,2010,36(16):189-191.
[4]同济大学应用数学系.高等数学(第五版)[M].北京:高等教育出版社,2002.
[5]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004.
[责任编辑王新奇]
Vol.18No.3Jul.2015

