线性矩阵方程的迭代求解方法
蔺小林, 霍佩佩
(陕西科技大学 理学院, 陕西 西安 710021)
线性矩阵方程的迭代求解方法
蔺小林, 霍佩佩
(陕西科技大学 理学院, 陕西 西安710021)
摘要:在很多问题中会遇到线性矩阵方程的求解问题,如果线性矩阵方程用矩阵直积和矩阵按行或按列进行拉直,用向量表示未知数不仅不方便,而且占用空间较大,因此有必要讨论线性矩阵方程的数值求解方法.本文给出了线性矩阵方程的迭代求解方法,讨论了迭代方法收敛的条件,给出了线性矩阵方程的雅可比迭代方法和方阵乘幂求和方法,用数值例子基于Matlab程序验证了算法的可行性.
关键词:线性矩阵方程; 雅可比迭代法; 收敛性; 方阵乘幂求和法
0引言
在科学计算和工程技术中常常会遇到线性矩阵方程的求解问题.在矩阵论中,线性矩阵方程的求解往往应用矩阵直积(Kronecker积)和矩阵按行或按列进行拉直[1],把线性矩阵方程的求解转化为线性代数方程组求解问题[2],这种方法可以求解多种类型的线性矩阵方程,从理论推导上比较完整,但在实际求解过程中,要求矩阵的逆,从计算的角度来看是不现实的[3,4].同时,在线性矩阵方程中,把未知量矩阵按行或按列进行拉直后,大规模的向量表示不便于观测与管理,且在计算机的存储中占用较大空间,因此有必要研究线性矩阵方程的数值迭代方法.
对线性矩阵方程求解,当然也可以求出其精确解,但是在实际问题中,要求得其精确解可能有较大困难,要耗费较长的时间.因此,类似于线性代数方程组可以使用迭代法求出其满足一定精度要求的数值解就可以[5-8].本文对线性矩阵方程的数值求解方法进行初步研究,给出了线性矩阵方程数值求解的迭代格式和迭代格式收敛的条件,引入了线性矩阵方程的雅可比迭代法以及方阵乘幂求和方法.最后,应用数值例子进行了验证.
1线性矩阵方程数值求解的基本迭代格式
考虑如下形式的线性矩阵方程:
(1)
采用矩阵记号,式(1)可写成
AX=B
(2)
其中A∈Rn×n为非奇异矩阵,且假设aii≠0(i=1,2,…,n),X∈Rn×s,B∈Rn×s,其中,系数矩阵



A=M-N,其中M,N为待定矩阵,并且矩阵M可逆,则式(2)变化为
X=M-1NX+M-1B,
选取初始值X(0),由迭代格式
X(k)=M-1NX(k-1)+M-1B (k=1,2,…)
(3)

1.1线性矩阵方程数值求解的基本收敛定理
类似于线性代数方程组的数值求解方法,我们给出由迭代格式产生的矩阵序列{X(k)}收敛的充分必要条件.
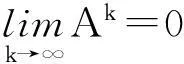
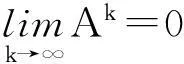
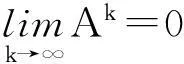
定理1对线性矩阵方程
X=GX+F
(4)
其数值求解的迭代格式为
X(k)=GX(k-1)+F
(5)
对任意初始值X(0)∈Rn×s,有下列收敛结果:
(1)迭代格式(5)产生的矩阵序列收敛的充要条件是矩阵G的谱半径满足ρ(G)<1;
(2)迭代格式(5)产生的矩阵序列收敛的充分条件是矩阵G的某种范数满足‖G‖<1.
证明:(1)必要性设(5)收敛,不妨设X(k)收敛到X*∈Rn×s,则X*满足(4),即X*=GX*+F,结合迭代格式(5),有
X(k)-X*=G(X(k-1)-X*)=…=Gk(X(0)-X*),
由引理1可知

又由引理2可知ρ(G)<1.


因为ρ(G)<1,所以由引理2可知

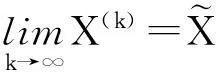
(2)由于‖G‖<1,所以(4)有唯一解,记为X*,则X*=GX*+F,结合迭代格式(5)有
X(k)-X*=G(X(k-1)-X*)=…=Gk(X(0)-X*)
故
‖X(k)-X*‖≤‖G‖‖X(k-1)-X*‖≤……≤
‖G‖k‖X(0)-X*‖
定理2对线性矩阵方程(4)及数值求解迭代格式(5),如果矩阵G的某种矩阵范数满足‖G‖=q<1,则矩阵迭代序列{X(k)}收敛,且对任何X(0)有
(1)‖X(k)-X*‖≤qk‖X(0)-X*‖;


证明:由定理1的结论可知矩阵迭代序列{X(k)}收敛.
(1)显然有关系式
X(k)-X*=G(X(k-1)-X*)
及
X(k+1)-X(k)=G(X(k)-X(k-1)),
于是有
‖X(k)-X*‖≤q‖X(k-1)-X*‖
(6)
‖X(k+1)-X(k)‖≤q‖X(k)-X(k-1)‖
(7)
反复利用(6)即得(1).
(2)由于
‖X(k+1)-X(k)‖=‖X*-X(k)-(X*-X(k+1))‖≥
‖X*-X(k)‖-‖X*-X(k+1)‖≥
(1-q)‖X*-X(k)‖,
即


(3)反复利用(7),结合(2)即可得到(3),证毕.
1.2线性矩阵方程数值求解的雅可比迭代格式
类似与线性代数方程组的数值求解方法,对线性矩阵方程的数值求解,也可以得到雅可比等迭代格式,为此引用下列记号
A=-L+D-U
(8)
其中



从式(1)的第ij个方程中解出xij(i=1,2,…,n;j=1,2,…,s)得到
(9)
选定初值X(0)∈Rn×s,把迭代前的值代入上式右边,由迭代格式计算得到的值作为下一次迭代的新值,再把这个新值代入右边依次进行计算.如此反复,也就是对k=1,2,…,计算
(k=1,2,…)
(10)
对该式采用矩阵A分裂记号,由式(10)得,
DX(k)=(L+U)X(k-1)+B
从而得到雅可比迭代格式的矩阵表示的紧凑形式
X(k)=D-1(L+U)X(k-1)+D-1B(k=1,2,…)
(11)
1.3线性矩阵方程数值求解的方阵乘幂求和方法
由线性矩阵方程数值求解的基本迭代格式(5)可知,给定初始值X(0),则
当矩阵G满足迭代序列收敛的充分必要条件ρ(G)<1时,有Gk→O(k→∞),其中O表示n阶零方阵.通过递推可得出矩阵方程的解的形式为
(12)
由此将矩阵方程的求解问题转化为求和问题[9].在求方阵乘幂序列(12)的求和过程中可使用如下迭代方法:

(13)
其中T(i)为n阶方阵,I为n阶单位阵.
实际计算中,求解T后就需要进行一次乘以F的运算,这样根据公式(13)可以推算出如下递推算法:

(14)
其中TX(k)∈Rm×n,G、F分别为公式(12)中的n阶方阵和m×n阶矩阵.由上述推导可以得到,当ρ(G)<1时,X(k)≈TX(k).如果取X(0)=0,则X(k)=TX(k).
2数值例子
例1对于矩阵方程AX=B,已知

试用雅可比迭代法求解,要求‖X(k)-X(k-1)‖∞≤10-5.
解:

雅可比迭代法迭代时的迭代格式为



故只要迭代三次就可以得到精确解.
事实上,可以证明,若ρ(G)=0,对迭代格式X(k)=GX(k-1)+F产生的矩阵迭代序列,最多迭代n次就可得到X=GX+F的不动点.
例2对于矩阵方程AX=B,已知,

解:可以验证,雅可比迭代法的迭代矩阵的谱半径小于1,我们省略详细Matlab求解程序和过程,只给出每次迭代的数值结果.
用雅可比迭代法求解的结果:



显然‖X(10)-X(9)‖∞≤10-3.
用方阵乘幂求和法求解,取G=D-1(L+U),F=D-1B,计算结果为:



显然,‖TX(10)-TX(9)‖∞≤10-3.
3结论
本文对线性矩阵方程的数值求解方法进行了讨论,得到了线性矩阵方程数值求解方法的收敛性定理和误差估计,给出了雅可比迭代方法以及方阵乘幂求和方法.线性矩阵方程的数值求解方法是线性代数方程组数值求解方法的推广,当线性矩阵方程的未知量矩阵是列向量时,本文方法就是线性代数方程组数值求解方法.因此,可以考虑把一些线性代数方程组数值求解方法推广到线性矩阵方程数值求解方法上来,比如线性代数方程组数值求解方法的多分裂方法、松弛因子方法等等, 这些问题将是我们需要进一步研究的问题.
参考文献
[1] 程云鹏.矩阵论[M].第2版.西安:西北工业大学出版社,2000.
[2] 蔺小林.现代数值分析方法[M].北京:科学出版社,2014.
[3] 蔺小林,何玉辉.一类矩阵方程的简便解法[J].陕西科技大学学报(自然科学版),2003,21(2):107-109.
[4] 蔺小林.矩阵方程AXB+CXD=E的解法研究[J].陕西科技大学学报(自然科学版),2003,21(5):13-15.
[5] 史文谱,刘迎曦,褚京莲,等.求解线性方程组的一种新方法[J].计算力学学报,2003,21(6):715-720.
[6] 陈飞武,赵小红.大型线性方程组的迭代求解[J].物理化学学报,2009,25(10):2 143-2 146.
[7] 刘长河.解线性方程组的迭代方法研究[J].北京建筑工程学院学报,2013,29(4):65-67.
[8] 郑亚敏.迭代法解线性方程组的收敛性比较[J].江西科学,2009,27(5):659-661.
[9] 张志斌,李世作,青剑,等.用方阵乘幂求和法求线性方程组的数值解[J].大学数学,2008,24(6):197-201.
On the iterative method of linear matrix equation
LIN Xiao-lin, HUO Pei-pei
(College of Science, Shaanxi University of Science & Technology, Xi′an 710021, China)
Abstract:We often encounter the problem of solving linear matrix equations in a number of situations such as Kronecker product and transform a matrix by line or by column into a vector.It is inconvenient to represent unknown variables with a vector and it will occupy a large space inevitable.Therefore,it is very necessary to search the solution of linear matrix equations.In this paper,we formulate an iterative procedure to solve linear matrix equations,discuss the convergence condition of our iterative procedure and present the Jacobi method and the summation of square matrix′s power of linear matrix equations.Numerical experiments based on Matlab show the effectiveness of the proposed algorithm.
Key words:linear matrix equations; Jacobi iterative method; convergence; summation of square matrix′s power (SSMP)
中图分类号:O151.21
文献标志码:A
文章编号:1000-5811(2015)01-0175-04
作者简介:蔺小林(1961-),男,陕西洛川人,教授,博士,研究方向:数值计算理论及其应用
基金项目:陕西省科技厅重点实验室科研计划项目(2011HBSZS014); 陕西科技大学学术团队计划项目(2013XSD39)
收稿日期:*2014-12-01 *2014-11-23

