关于全概率公式及其实际应用

杨　波

(阜阳师范学院 数学与统计学院，安徽 阜阳　236041)

关于全概率公式及其实际应用

杨波

(阜阳师范学院 数学与统计学院，安徽 阜阳236041)

摘要：通过对全概率公式的分析得出此公式主要用于由原因求结果的概率。同时借助具体的事例说明了如何恰当的划分完备事件组，把全概率公式应用于产品检验、传染病的诊断和经济决策上。

关键词：全概率公式；完备事件组;复杂事件；简单事件

作者简介：杨波,硕士，讲师，阜阳师范学院。

基金项目：国家级特色专业“数学与应用数学”建设项目(NO.TS11496)资助。

文章编号：1672-6758(2015)11-0052-3

中图分类号：O211.1

文献标识码：标识码：A

Abstract：The paper argues that the total probability formula is mainly used in the probability analysis of the result and reason. How to properly divide the complete event group is illustrated in the paper with some examples, and the total probability formula can be applied to the product inspection, the diagnosis of infectious diseases and economic decision-making .

一引言

在实际生活中我们经常会遇到有关于概率计算的各种问题，而实际问题的解决是很复杂的，全概率公式多用于计算复杂事件的概率，将问题化繁为简。使用全概率公式解决问题可以借助引入各种小前提，将事件分解为两个或是若干个互不相容的简单事件的并集，并且在每个小部分中可以比较容易地求得所需要的概率，再用加法公式求出复杂事件的概率，所以全概率公式多用于化简复杂的概率计算问题。

本文探讨了全概率公式的意义以及在产品检验,传染病的诊断和经济决策上的应用，同时给出了运用全概率公式解决实际问题时的分析方法，体现出全概率公式的具体作用 。

二全概率公式

定义 1如果n个事件A1，A2，…，An满足以下两个条件：

(1)A1，A2，…，An两两互不相容；

(2)A1∪A2∪…∪An=Ω；

那么，我们称这个n个事件A1，A2，…，An构成样本空间Ω的一个划分，也称构成一个完备事件组。

定理 1设n个事件A1，A2，…，An构成样本空间Ω的一个划分，B是一个事件。当P(B)>0,P(Ai)>0, i=1,2,…,n,则

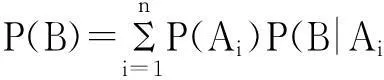
这个公式称为全概率公式。

使用全概率公式的基本思想就是将一个复杂事件的概率化简为求几个独立简单事件的概率和。化简的关键是如何将一个事件A合理的划分为一个互不相容的事件组A1，A2，…，An,使得B出现的同时有且只有一个Ai(i=1,2,…,n)同时出现，如下图所示.然后再利用条件概率公式和加法公式便可得全概率公式。

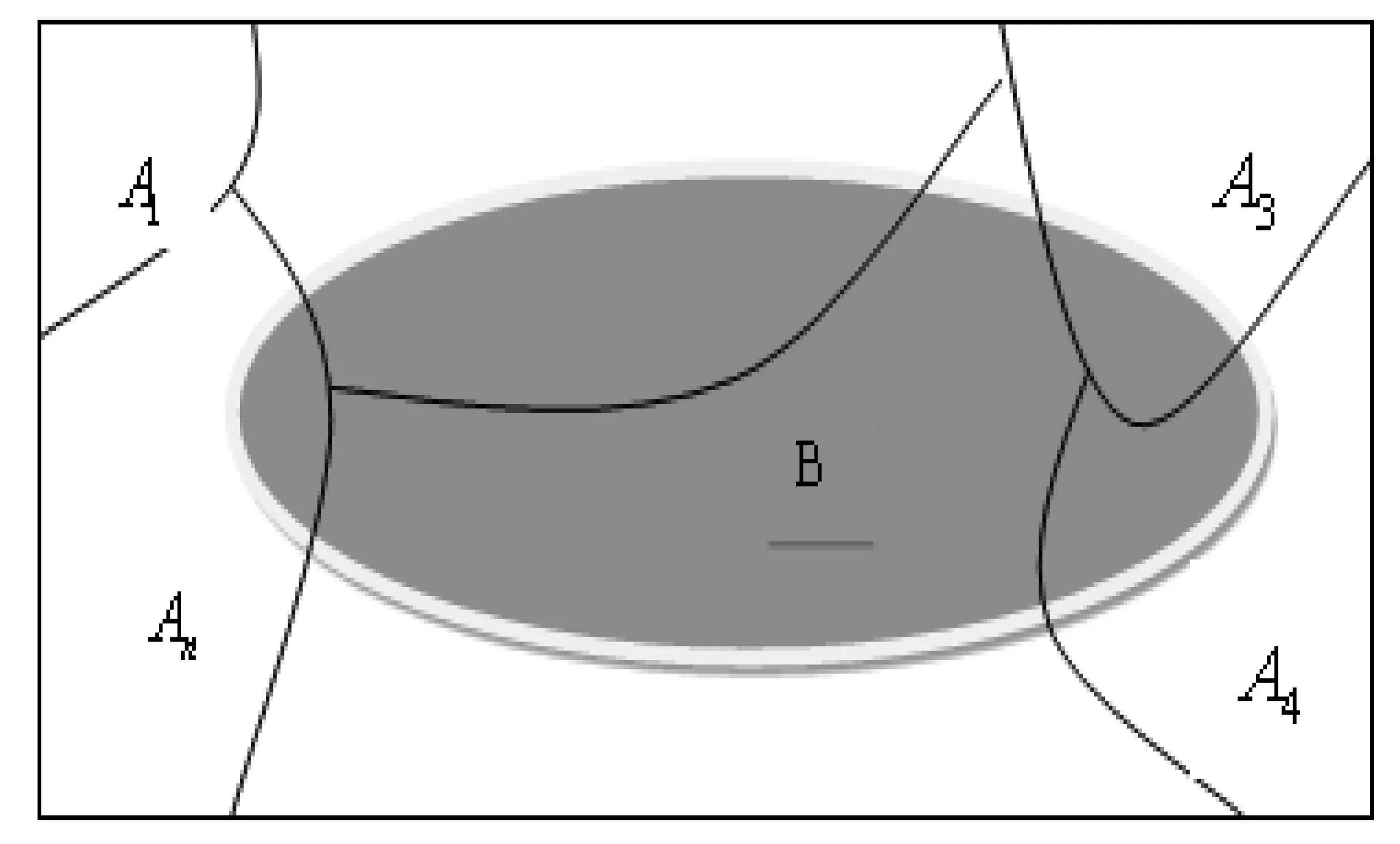
图1

这里BAi就是“简单事件”,再利用乘法公式，可求得它们发生的概率为

P(BAi)=P(Ai)P(B|Ai)，

式中P(Ai)是导致事件B发生的若干个不同原因的概率，往往是题中给出的或者是能求出的。P(B|Ai)所表示的是在若干个原因事件Ai发生的条件下事件B发生的概率，它可以从题目的已知条件直接得出或间接导出.因此在应用此公式的时候，首先要明白如何划分完备事件组，再应用此公式。

三全概率公式在实际生活中的应用

运用全概率公式，我们可以利用问题产生的原因来求得此问题结果的概率，即由因求果。实际应用时，应先充分分析某一结果产生的原因，将这些原因构成一个完备事件组，再求在每一种原因下问题发生的概率，最后将这些概率求和，即得到该问题结果的概率。下面，我们分别讨论全概率公式在产品检验，传染病诊断和经济决策中的应用。在应用时，重在弄清楚事件相互影响的次序，恰当地划分完备事件组。

1.在产品检验上的应用。

在实际生产过程中，一批产品被生产出来，检验人员会在出厂前进行一次抽样检查，检查合格后才会发货。而卖家收到货之后，还会再进行简单的验货。所以要保证卖家的验货合格，厂家就要对检验结果分析，进行一定的概率计算，这里就可以使用到全概率公式。

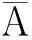
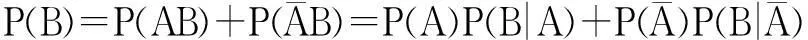
例1某工厂生产一种儿童玩具，工厂检验员在发货前进行检验。假设该批玩具一共有1000个，正品率为0.999，检验员随机抽了一件，则卖家收到货后再随机抽到的是次品的概率？

解设A={检验员抽到的的是次品}，B={卖家抽到的是次品}

因为检验员抽到的结果直接影响到卖家的结果，则

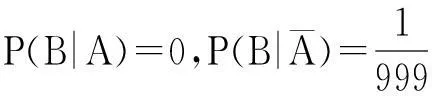
又由题意知，

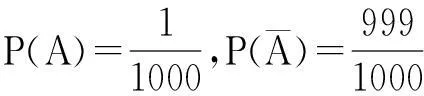
于是由全概率公式得

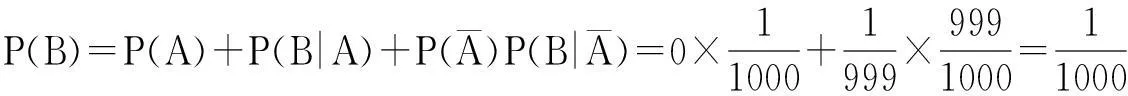
由这个计算结果我们可以看到，检验员抽到次品的概率和卖家抽到次品的概率是一样的，就如一些彩票，无论先买后买，获奖的概率都是一样的，也正是因为这样，检验员的检查结果可以客观的反映这批产品的质量，所以出厂前的检验是必要的。

2.在传染病诊断中的应用。

对传染病的控制，最重要的步骤之一是传染病的确定，诊断出是哪一种传染病，是治疗的前提。要对患者进行诊断，化验可能很繁琐，但是运用全概率公式,可达到简化化验过程，缩短治疗时间，较快治愈病患的作用。对于传染病的诊断，我们可以将传染病的致病菌的全体看成样本空间，然后将这个致病菌的全体进行划分。下面我们以流感为例，说明全概率公式在其中的应用。对于此类问题，具体的过程可以如下。

设A={某地发现一种流感}，该流感是由B1,B2,…,Bn种致病菌的中的一种引起的。由于结果A产生的原因是这n种致病菌，于是可将这n种致病菌组成样本空间Ω的一个完备事件组.假设P(Bi)>0，则可以得到该流感由其中一种致病菌Bi引起的概率为

由乘法公式

P(ABi)=P(Bi)P(A|Bi)，

及全概率公式

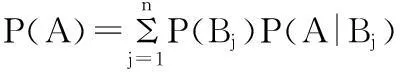
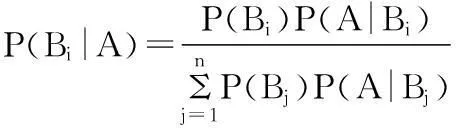
这个式子实际上就是著名的贝叶斯公式，该公式为病人的确诊提供参考。

例 2某地区爆发了一种禽流感，为了控制疫情，科学家对患病的禽类进行检验分析后，初步确认这种禽流感可能是1号，2号，3号这三种致病菌中的一种引起的。已知禽类感染1号致病菌的可能性为45%，感染后的发病的概率为0.90;感染2号致病菌的可能性为40%,感染后发病的概率为0.80；感染3号致病菌的可能性为15%，感染后发病的概率为0.75。问这种流感是2号致病菌引起的概率是多少？

解 设A={某地爆发一种禽流感}, Bi={这种禽流感是由i号致病菌引起的}(i=1,2,3). 由题目知

P(B1)=0.45P(B2)=0.4,P(B3)=0.15.

P(A|B1)=0.9P(A|B2)=0.8,P(A|B3)=0.75

由条件概率公式

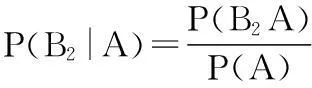
而P(B2A)=P(B2)P(A|B2),又根据全概率公式知

P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|P3),

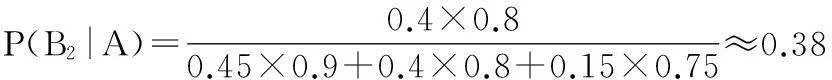
所以可知这种禽流感是2号致病菌引起的概率为0.38。

3. 在经济领域的应用。

在经济决策前，要初步拟定几个备选方案，然后对各个方案进行评估，最终确定最优的方案，以达到最大化的经济收益，这是管理决策者要做的事情，全概率公式可以应用于对各种方案的评价，帮助做出最后的选择。对于此类问题，各种经济决策方案就是对总体的一个划分，然后再计算在每种决策的前提下，获利的可能性。

例3有一家牛奶厂，有三个奶源地，分别是黑龙江，新疆，西藏。由调查结果知这三个奶源地的合格率分别为0.96，0.94，0.95。三个奶源地的供奶量占该厂产量的40%，30%，30%。该厂将运过来的牛奶集中加工，再出售。一位投资商打算投资该厂，他随机抽取了一件牛奶，如果合格率达到95%就投资，问他最终会不会投资？

分析 这题实际是计算抽取一件牛奶的合格率，由于抽出合格品的原因是它来自三个奶源地，所以可以将三个奶源地构成一个完备事件组，然后由全概率公式可得合格率，再根据结果判断要不要进行投资。

解 A={取到的是合格品},B1={抽出的牛奶是黑龙江供的},

B2={抽出的牛奶是新疆供的},B3={抽出的牛奶是西藏供的}.

由条件知

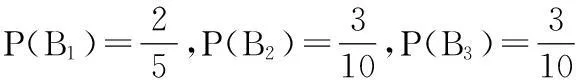
P(A|B1)=0.96,P(A|B2)=0.94，P(A|B3)=0.95.

据全概率公式可得

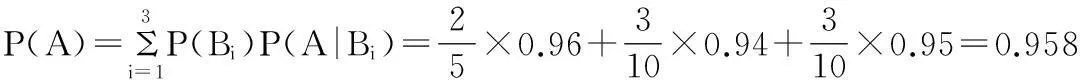
所以由计算结果可知，该投资商应该多考虑考虑。

四结论

全概率公式能够有效地解决一些繁琐的问题。在遇到一些使用一般方法处理十分麻烦且容易出错的多个复杂问题时，如果可以把其中一个复杂事件分割成互不相容的几个简单事件时，那就可以使用全概率公式。在应用时，需要将样本空间进行恰当的分割，使原本复杂的问题转变为几个个简单事件，再使用条件概率计算每个简单事件的概率，最后运用加法公式将所有结果进行相加就能得出结果，这也就是全概率公式的意义所在。

参考文献

[1]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社，2004：38-50.

[2]杜镇中.全概率公式及其应用[J].遵义师范学院学报，2005，7 (5)：76-78.

[3]张丽，闫善文，刘亚东.全概率公式与贝叶斯公式的应用及推广[J].牡丹江师范学院学报，2005(1)：15-17.

[4]顾晓青.全概率公式的应用[J].沧州师范专科学校学报，2000，16(2)：42-43.

[5]王妍.概率统计在实际问题中的应用举例[J].中国传媒大学学报自然学版，2007,14(1)：15-19.

Applications of the Total Probability Formula

Yang Bo

(School of Mathematics and Statistics, Fuyang Teachers College, Fuyang, Anhui 236041，China)

Key words：total probability formulas; complete event group；complex event; simple event

Class No.:O211.1Document Mark：A

(责任编辑：蔡雪岚)