环境星NDVI时间序列重构方法研究

环境星NDVI时间序列重构方法研究

李天祺1，2，朱秀芳1，2，潘耀忠1，2，刘宪锋1，2

(1.北京师范大学 地表过程与资源生态国家重点实验室，北京 100875；2.北京师范大学 资源学院，北京 100875)

摘要：利用目前时间序列曲线重构中较为常用的非对称高斯函数拟合、Double-Logistic曲线拟合、S-G滤波和时间序列谐波分析法对环境星NDVI时间序列进行重构处理。分析了上述4种植被指数时间序列重构方法对环境星数据的适用性。实验结果表明，对于环境星数据，在4种方法中非对称高斯函数拟合、Double-Logistic曲线拟合法更适用于对植被地物的时间序列进行重构，对照参考数据，其重构曲线对植被物候的表达有较高的一致性；而时间序列谐波分析法对原始数据的扰动最小，适用于非植被地物的时间序列重构；S-G滤波在4种方法中的重构效果最差。

关键词：时间序列；环境星；非对称高斯函数拟合；Double-Logistic曲线拟合；S-G滤波；时间序列谐波分析法

doi:10.3969/j.issn.1000-3177.2015.01.010

中图分类号：TP79文献标识码：A

收稿日期：2014-02-21修订日期：2014-04-11

基金项目：国土资源部公益性行业科研

作者简介：杨进生(1959～)，男，高级工程师，主要从事水文地质环境地质遥感技术方法研究。

NDVI Time-series Reconstruction Methods of China’s

HJ Satellite Imagery

LI Tian-qi1,2,ZHU Xiu-fang1,2,PAN Yao-zhong1,2, LIU Xian-feng1,2

(1.StateKeyLaboratoryofEarthSurfaceProcessesandResourceEcology，BeijingNormalUniversity，Beijing100875；

2.CollegeofResourcesScienceandTechnology，BeijingNormalUniversity，Beijing100875)

Abstract：In this paper，we compared the performance of four NDVI time-series reconstruction methods，including asymmetric Guassian function fitting (A-G)，double logistic function fitting (D-L)，Savitzky-Golay filtering method (S-G) and harmonic analysis of time series (Hants)，on processing the imagery of China’s HJ satellites. Results show that A-G and D-L are more suitable for reconstruction of vegetation features，comparing with the reference data. The reconstruction curves of A-G and D-L have high consistency in expression vegetation phenology. Hants brings minimal disturbance of the original data and fits for reconstruction of architectural features and water features. S-G performs worst.

Key words：time-series；China’s HJ satellite；asymmetric Guassian function fitting；double logistic function fitting；Savitzky-Golay filtering；Hants

1引言

归一化植被指数(Normalized Difference Vegetation Index，NDVI)是反映植被生长状态及植被覆盖度的最佳指示因子，也是季节变化和人类活动影响的重要指示器[1]。在遥感研究中，随着高时间分辨率数据(NOAA/AVHRR、TERRA/MODIS、SPOT/VEGETATION)的应用，归一化植被指数时间序列作为反映地表状况的连续信号，已经广泛地应用于环境动态变化监测[2-3]、植被物候信息提取[4-5]、土地覆盖/利用分类及监测[6-7]等诸多领域，是生产研究的重要数据源之一[8]。

然而，由于传感器角度变化、云或霾的干扰、数据传输误差、二向性反射或地面冰雪覆盖的影响，使得NDVI时间序列曲线有明显的突升或突降，导致植被物候信息难以辨别[9-10]。NDVI时间序列中噪声的存在限制了该数据的深入应用，因此在应用前必须有效地去除噪声、重构时间序列[11]。对此，许多关于NDVI时间序列降噪、重构的方法被提出、评价以及用于实际研究[12]。目前，主要的NDVI时间序列重构方法可分为：基于阈值去噪法(如最佳指数斜率提取法(BISE))、基于滤波的平滑方法(如Savitzky-Golay滤波法、时间序列谐波分析法(Hants)、傅里叶变换)和非线性拟合法(如Double-Logistic曲线拟合法和非对称高斯函数拟合法)，这些方法已广泛应用于全球不同区域的研究中[13]。

不同的重构方法有其各自优点，对不同区域或不同数据源的适用性也不同。因此，国内外学者在方法重构效果方面做了大量的对比研究。例如Beck以芬兰、瑞典、挪威的交界区域为研究区，利用Double-Logistic曲线拟合法、非对称性高斯函数拟合法和傅立叶变换法对MODIS NDVI产品进行重构比较研究，认为Double-Logistic曲线拟合和非对称性高斯函数拟合的重构效果相似，且均优于傅立叶变换的方法[14]；Jennifer选择加拿大洛矶山脉中的一个典型区域作为研究区，利用MODIS NDVI产品对比6种NDVI时间序列重构方法，认为Double-Logistic曲线拟合与非对称高斯函数拟合在总体上优于其他4种滤波方法[15]；Chen利用SPOT Vegetation产品以中国为研究区，对多类地物的NDVI时间序列进行重构研究，得出通过改进的Savitzky-Golay滤波法在NDVI曲线重构上优于最佳指数斜率提取法(BISE)与傅里叶变换(FT)的结论[16]；Julien利用GIMMS/NDVI数据集对比IDR(Iterative Interpolation for Data Reconstruction)方法与HANTS、Double-Logistic曲线拟合法的重构效果，认为IDR方法在3种方法中的重构效果最好，但在强噪声中对NDVI低值存在过度拟合[17]。

环境星全称为环境与灾害监测预报小卫星星座，A、B星(HJ-1A/1B星)，于2008年9月投入使用。重访周期为2天，所搭载的CCD相机具有可见光及近红外4个波段，空间分辨率为30m，具有宽幅、中高分辨率的特点，适用于区域的大范围中尺度覆盖监测。环境星对我国生态、环境变化和灾害监测，反映生态环境发展过程，以及生态环境发展变化趋势的预测均有着重要意义[18]。环境星反演的NDVI时序序列数据已经被广泛的应用于植被变化监测、农作物面积测量及长势监测、灾害监测以及土地覆盖/利用的划分中。然而，目前尚无有关各类重构方法在环境星NDVI数据重构研究中的适用性的报道。为此，本文综合目前国内外研究成果，选取当前4类主要的重构方法，分析适用于环境星数据的植被指数时间序列重构方法，以改善环境星在植被动态变化监测、土地覆盖/利用分类等方面的应用效果。

2研究区及数据

2.1研究区

本研究以北京为研究区。北京位于华北平原西北边缘，地处115°20′E～117°30′E，39°28′N～41°05′N，地势西北高、东南低。西部、北部和东北部三面环山，东南部是向东倾斜的平原。北京市总面积16807km2，其中山区约占总面积的62%，平原约占38%。研究区属北温带大陆性季风气候，具有分明的四季划分。

2.2实验数据

研究中所用数据包括环境星多光谱数据和MODIS产品(MOD13Q1)。其中环境星数据为2012年2月到11月北京地区环境星星座多光谱影像(近红外波段：760nm～903nm，红波段：630nm～693nm，绿波段：520nm～603nm，蓝波段：430nm～523nm)，影像大小为5926×5987像元，空间分辨率为30m，一共为28景，平均时间间隔为10天；MODIS植被指数产品(MOD13Q1)为基于16天最大值合成法的植被指数数据，空间分辨率为250 m，该产品经过几何纠正和大气校正，产品中NDVI数据和QA(Quality Assessment)用于本实验研究。

图1　实验数据

2.3环境星数据预处理

环境星数据预处理包括辐射定标、大气校正、几何纠正和植被指数时间序列生成。首先，对环境星数据的辐射定标采用2011年中国资源卫星应用中心公布的HJ-A/B星绝对辐射定标系数，将传感器DN值标定为反射率；其次，大气校正采用FLAASH模型进行校正，该模型在环境星数据的大气校正中能够很好地消除大气的影响[19]；几何纠正以带有精确地理坐标的TM影像为参考对环境星影像进行配准，其中TM影像的观测时间为2011年7月26日，配准误差控制在1个像元以内；最后，对28景影像逐像元计算NDVI，并进行波段融合，但由于大面积云污染等天气原因及传感器时间分辨率的限制，现有的高质量环境星NDVI数据并非等时间间隔，考虑植被在短时间(10天～16天)的生长特性，通过线性插值的方法[12]，将现有28期NDVI数据插值为等时间间隔的27个波段，时间间隔为11天。

3研究方法

3.1典型地物原始时序曲线

研究中选取北京地区的6种典型地物进行分析，分别为林地、草地、单季作物、双季作物、水体、建筑，其中单季作物以春小麦为主，双季作物以冬小麦-夏玉米为主。在本研究中，参考北京地区高分辨率遥感影像及2012年农作物目视解译分类结果，每类地物选取50个～80个样本像元，共选取390个像元，并对每类样点求其NDVI均值，构建该类别的原始时序曲线并对其进行重构，原始曲线如图2所示。

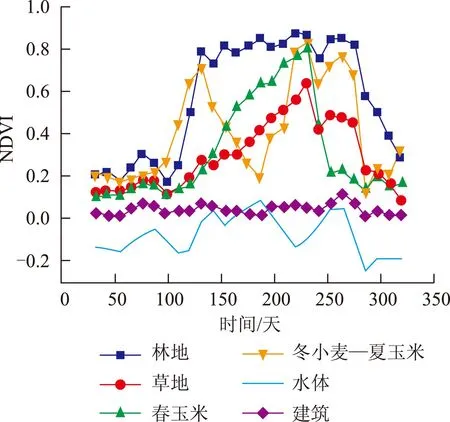
图2　环境星原始NDVI时序曲线

3.2典型地物时序曲线的重构

3.2.1非对称高斯函数拟合法(Asymmetric Gaussian model，A-G)

非对称高斯函数拟合法是基于高斯函数的分段最小二乘拟合算法，由Jönsson等在2002年提出[4]，该方法的拟合函数形式如下：

f(t) =f(t;c1,c2,a1,a2,a3,a4,a5)=

c1+c2g(t;a1,a2,a3,a4,a5)

(1)

其中，g(t;a1,a2,a3,a4,a5)为高斯函数：

g(t;a1,a2,a3,a4,a5)=

(2)

其中，c1,c2决定曲线的基准和幅度；a1为曲线最大值或最小值在时间轴上的位置；,a2,a3,a4,a5分别决定左右半曲线的宽度和陡峭度。非对称高斯函数拟合法的处理过程分为区间提取、局部拟合和整体连接3个步骤[20]。

3.2.2Double-Logistic曲线拟合法(D-L)

Double-Logistic曲线拟合法是由Beck等[20]于2006年提出的一种非线性最小二乘拟合算法，与非对称高斯函数拟合法类似，也属于分段拟合。其函数形式如下：

NDVI=wNDVI+(mNDVI-wNDVI)×

(3)

其中，wNDVI和mNDVI分别为冬季NDVI和全年NDVI的最大值，S、A代表曲线上升拐点和下降拐点，mA和mS分别代表这两点处NDVI的上升和下降速率。在处理过程上，Double-Logistic曲线拟合法与非对称高斯函数法类似，即利用曲线极值将时间序列分成多个区间，对每个区间进行局部拟合，最后对拟合出的各段曲线进行整体连接。

3.2.3Savitzky-Golay滤波法(S-G)

Savitzky-Golay滤波法最初由Savitzky和Golay于1964年提出，后由Chen等[16]对其进行改进，是一种基于最小二乘卷积的移动平均算法，其权重取决于在一个滤波窗口范围内做多项式最小二乘拟合的多项式次数[13]。其基本公式如下：

(4)

其中，Y为原始NDVI值，Y*为平滑后的NDVI值，Ci是从过滤窗口首部开始的第i个NDVI值的权重，N是窗口宽度，且N=2m+1。其中窗口宽度与多项式拟合的阶数由人为设定。Savitzky-Golay滤波法的处理过程如下[16]：

①对时间序列的长期变化趋势进行拟合，将原始NDVI值分为“真值”和“假值”两类；

②通过局部循环迭代，使得原始值中的“假值”点被Savitzky-Golay重构值替代，与“真值”点构成新的NDVI曲线；

③重复上述过程，直至拟合结果足够接近NDVI时序曲线的上包络线。

3.2.4时间序列谐波分析法(Hants)

时间序列谐波分析法(Harmonic analysis of time series，Hants)是基于傅里叶变换改进的一种时序曲线重构方法[21]，通过傅里叶变换将时序曲线表示为不同相位、幅度和频率的正弦函数组合，其表达式为：

(5)

其中，A0为谐波的余项，等于时序曲线的平均值；Aj为各谐波的振幅；ωj=2jπ/N为各谐波的频率，N为时间序列的长度；θj为各谐波的初始相位；m=N-1为谐波个数。

原始时序曲线经傅里叶变换后，Hants方法通过对新序列中几个最为显著频率的傅里叶序列进行最小二乘拟合对原始曲线重构，该过程经多次迭代直至重构曲线中没有被污染点或达到某一迭代阈值。拟合过程中，原始序列中的低频部分被保留，高频部分作为噪声被去除。Hants算法在对时序曲线处理时，需要设置显著频率、误差阈值、最大删除点数及有效数据范围。

3.3重构效果评价方法

本研究选取北京地区的6种典型地物进行分析，分别为林地、草地、单季作物、双季作物、水体、建筑，其中单季作物以春小麦为主，双季作物以冬小麦-夏玉米为主。针对植被地物与非植被地物分别采取物候信息一致性与曲线相关性两种评价方法对重构效果进行评价。

3.3.1物候信息一致性评价

MODIS植被指数产品经MVC方法的初步处理可以有效地去除云污染和拟合缺损[8]，且MODIS植被指数产品在植被变化监测及物候信息提取等研究中，其物候信息反映的真实性在国内外有着广泛的认可。在本实验中林地、草地样本的分布具有较大区域的一致性，因此可排除混合像元对NDVI值造成的影响。在实验中选取高质量MODIS NDVI数据，可较为真实地反映地表林地与草地的NDVI变化；之后，利用同种重构方法对高质量MODIS NDVI时序曲线与相同地点的环境星NDVI时序曲线进行重构，并分别提取重构结果的物候信息，对二者进行比较，来评价各类重构方法在环境星时序曲线重构中的效果。在对植被生长的物候信息提取中采用Jönsson和Eklundh改进后的动态阈值法对物候信息进行提取，该方法在时间域和空间域上都具有很好的适用性[20]；其中，阈值设定为Jönsson在提出动态阈值方法时建议的生长季开始和结束的NDVI值是年振幅的20%[20]。

对于农作物(春玉米、冬小麦-夏玉米)，提取重构后时序曲线的作物生长信息，通过对比北京地区农作物物候历，对各类重构方法在环境星数据适用性进行评价；其中，返青期的提取采用与林地与草地相同的动态阈值法和动态阈值20%，由于农作物收割不属于植被的自然生长，且收割会使农作物NDVI值在短时间内大幅度下降，因此农作物收割时间采用最大斜率法进行提取。

最后，通过物候信息一致性的比较，以时间偏差对各重构方法的重构效果进行定量评价。

3.3.2曲线相关性评价

在曲线重构中，重构方法对原始数据会产生扰动，主要来自在重构过程中数据有效性判断、异常值剔除以及重构函数拟合这3个方面，且这3种扰动是不可避免的，所以在时序曲线重构中尽可能地缩小拟合值与原始值的差异，以减小重构方法对原始序列数据过度扰动[22]。非植被地物的NDVI时序曲线没有明显的生长峰值，因此，通过比较各重构方法对原始时序数据的扰动程度，来进行重构方法的评价。其中，扰动程度由原始曲线与重构曲线的相关统计量比较得出。

4实验结果与重构效果评价

4.1重构方法的实现

基于上述4种时间序列重构方法，研究中采用TIMESAT与IDL实现时间序列的重构。其中，A-G、D-L、S-G 3种重构方法基于TIMESAT 3.1.1平台，通过对比不同参数对重构结果的影响，以及参考国内外相关研究[16，20，23]。最终将参数设定如下：NDVI有效值域(Data Range)为-1～1，噪声去除阈值(Spike Method)为2，拟合峰值参数(Adaptation Strength)为3，迭代次数(Envelope Iterations)为2，滑动窗口大小(Window Size)为6或7；Hants方法的实现基于IDL-HANTS v1.3，其参数设置包括：最大下降偏移量(FET)为0.2，NDVI有效值域(Range)为-1～1，异常点最大数(TAT)为5，迭代次数(iMAX)为10，以及谐波频数。其中，谐波频数设置过小会导致拟合曲线过于平滑而缺失细节信息，此外谐波频数与植物生长季及参与拟合点个数相关，在本研究区内植物生长峰值数不超过3，且可满足参与拟合点个数大于最大频数的2倍减1。因此，在本研究中，谐波频数最小设置为2，最大设置为3。

4.2重构结果分析

本文为分析上述4种NDVI时间序列重构方法对环境星数据的适用性，对6类典型地物(林地、草地、春玉米、冬小麦-夏玉米、建筑及水体)的原始数据分别进行了时间序列的重构，重构结果如图3所示。

图3　环境星数据NDVI时间序列重构结果

图3中，经过4种重构方法处理后的NDVI时序曲线较原始曲线去除了由噪声带来的影响，整条曲线更为平滑。其中，植被时序曲线经过重构后更符合植物的生长特点，林地、草地、春玉米表现出一年单峰的生长特点，且均在8月达到峰值，冬小麦-夏玉米表现出一年两峰的生长特点，其波峰与波谷的位置也与北京地区冬小麦-夏玉米的播种—生长—收割时间较一致；非植被地物中，建筑经重构后的NDVI时序曲线变化不大，近似于某一常数，介于0～0.1之间，符合该类别的光谱反射特征，水体经重构后的NDVI普遍在0值以下，而夏季部分高值的出现为该时段水体表面的植物生长所致。因此，上述4种方法均可有效地对HJ数据进行NDVI时间序列重构。

4.3重构效果评价

为进一步区分各重构方法的差异，本研究从以下两方面对环境星数据的重构效果进行定量评价：①植被地物重构后的环境星时序曲线对物候信息反映的一致性评价；②非植被地物重构曲线与原始曲线的相关性评价。

4.3.1物候信息一致性评价结果

对林地、草地MODIS数据的重构采用与环境星数据相同的实验方法及重构参数。其中，在S-G滤波中，考虑MODIS数据的时间间隔为16天，而环境星数据为11天，因此滑动窗口大小设置为4或5(环境星数据为6或7)。MODIS重构结果如图4所示。

对重构后的环境星与MODIS时序曲线用同一动态阈值20%，分别提取林地与草地的返青期与枯黄期，并得到不同方法下返青期与枯黄期的时间偏差，如图5所示。从图5中可见，在4种方法中，D-L对环境星时序数据的重构效果最好，时间偏差均在5天以内，对林地及草地物候期的提取最为精确；S-G在两类植被地物的物候提取上偏差最大，其平均偏差在7天以上，其原因可能是环境星原始数据中的噪声较多，滑动窗口平均滤波的方法属于局部拟合，不能完全消除噪声的影响，而相比其他3种方法对数据整体进行半局部和全局拟合，能够更好地描述时序曲线的变化趋势和全局特征。A-G在林地返青期和枯黄期的提取精度均上要优于Hants，且Hants在重构中对原始数据在生长季外出现的假高值不能很好地处理，如图4(a)与图4(f)所示。在本实验林地数据中，出现在返青期前的假高值，Hants重构后并未将其消除，而在原始数据中没有假高值影响的草地类型重构中，利用Hants重构后的环境星时序曲线对返青期的提取结果要更为精确。

图4　MODIS数据的4种方法NDVI时间序列重构结果

对于农作物(春玉米、冬小麦-夏玉米)，提取重构后时序曲线的作物生长信息，对比北京地区农作物物候历，如表1所示。对图3中4种方法的重构曲线分别提取作物生长信息，其中，对春玉米提取返青(出苗)期和收获期；对冬小麦-夏玉米提取冬小麦的返青期、生长峰值期(抽穗)、夏玉米的生长峰值期(吐丝后期)和夏玉米的收获期；并将所提取的物候时间与表1中所对应时段的中间时刻进行比较，计算时间偏差，其结果如图6所示。

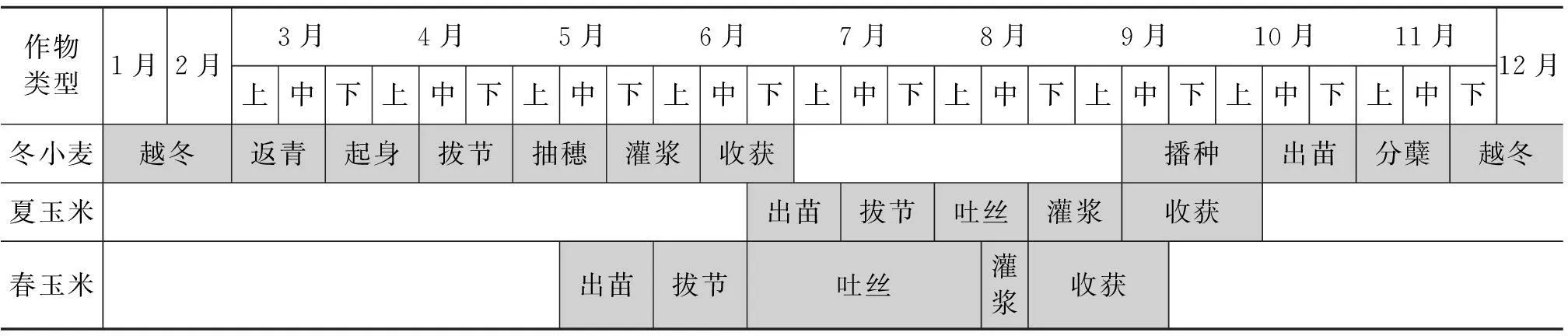
表1　北京地区农作物物候历

图5　不同方法重构后环境星与MODIS物候期差异

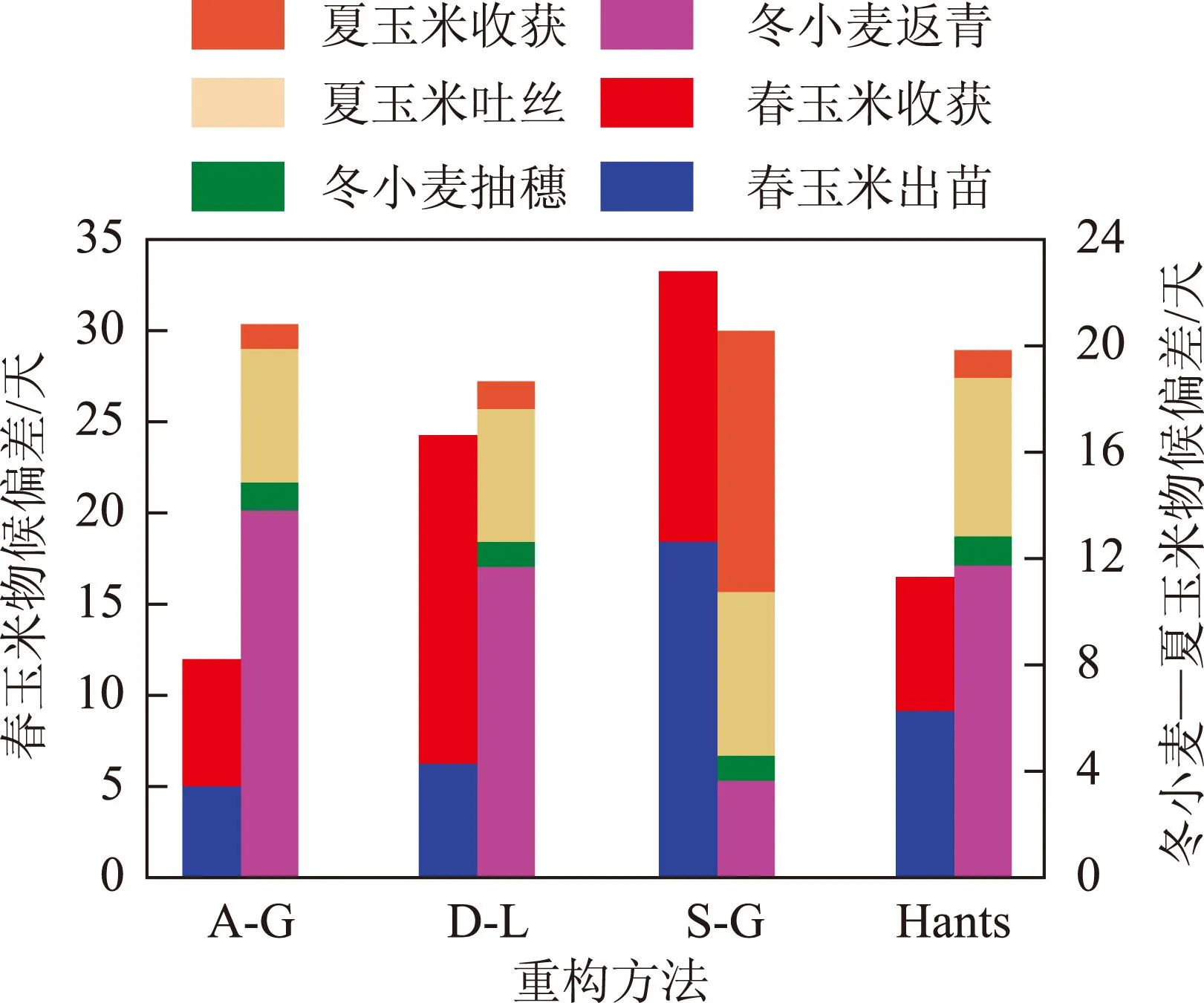
图6　环境星农作物在不同方法重构后的差异比较

从图6可以看出4种方法对环境星数据的重构结果中，A-G对单季作物春玉米的物候提取，偏差最小；在双季作物冬小麦-夏玉米物候的提取中，D-L重构效果略优于A-G与Hants的提取结果。相比A-G与Hants两种方法，在冬小麦返青期的提取中Hants偏差较小，在夏玉米生长峰值提取中A-G更为准确；综合两种作物的时间偏差，Hants的偏差最小，但由图3(d)中可以看出，Hants重构后的农作物曲线过于平滑，且峰值两边严格对称，这对存在人为影响的农作物，时序曲线中的非对称信息很难提取[24]。同上述林地与草地物候的提取，S-G对两类作物物候期的提取偏差最大，其原因为环境星数据噪声的影响与局部拟合方法有一定局限性。

4.3.2曲线相关性评价结果

选取原始曲线与重构曲线的最大值、最小值、均值、均方差及二者的相关系数进行重构方法的扰动程度比较，其比较结果如表2所示。

表2　原始曲线与4种方法处理结果对照表

从表2可以看出，经4种方法的重构，两种地物的原始曲线均达到了平滑的效果，其效果表现在曲线最大值的降低、最小值的升高与均方差的减小上；由于植被指数时间序列的噪声主要来自云、大气的影响，而造成值的下降，4种滤波方法中均有对此类异常值的判断与处理。可以看到在A-G、D-L和S-G 3种方法重构后，曲线均值相比原始曲线均有提高，而Hants重构曲线的均值保持不变，其原因是Hants方法是以傅里叶变换为原理的全局拟合。从数据整体减小了重构过程对原始数据的扰动，这一结论与表中重构曲线与原始曲线的相关系数一项的结果一致。综合上述结果，对于非植被地物，4种方法中Hants在重构过程中对原始数据的扰动最小，S-G其次，A-G与D-L由于为特定函数的半局部拟合，对原始数据的扰动均较大。

5结束语

本文以北京为研究区，比较分析了非对称高斯函数拟合、Double Logistic函数拟合、S-G滤波和谐波分析法这4种时间序列重构方法在环境星数据中的重构效果。通过植被物候信息比较和重构过程对原始数据的扰动分析，定量评价了这4种方法在植被地物的时序曲线重构中的效果，总体来看4种方法重构后的曲线都达到了对噪声的去除与对整体曲线的平滑。在植被物候信息的准确性上，对于林地与草地，Double Logistic函数拟合在环境星数据与高质量MODIS数据的重构中，植被物候信息的一致性最高，非对称高斯函数拟合与Hants效果次之。其中，Hants对非生长季内的假高值不能很好的处理，S-G偏差较大；在农作物时序曲线的重构中，对比农作物物候历，S-G在两类作物(单季与双季)中偏差均较大，A-G，D-L，Hants的精确性较高，但相比A-G与D-L的重构结果，Hants重构曲线无法反映收割对NDVI值造成的突降。对于水体与建筑这两类非植被地物，分析4种重构方法对原始数据的扰动程度，发现Hants重构后的曲线与原始曲线最为接近，相关系数较高；A-G，D-L对原始曲线的改动较大。

综上，对于环境星数据，A-G与D-L更适用于重构植被地物的时序曲线，可以很好地用于植被物候提取、植被变化监测以及农作物分类等研究；对非植被地物，Hants对原始时序数据的扰动最小，重构曲线更接近原始时间序列。

参考文献：

[1]赵英时.遥感应用分析原理与方法[M].北京：科学出版社，2003.

[2]LYON J G，YUAN D，LUNETTA R S，et al.A change detection experiment using vegetation indices[J].Photogrammetric Engineering and Remote Sensing，1998，(64)：143-150.

[3]PETTORELLI N，VIK J O，MYSTRUD A，et al.Using the satellite-derived ndvi to assess ecological responses to environmental change[J].Trends in Ecology & Evolution，2005，(20)：503-510.

[4]JONSSON P，EKLUNDH L.Seasonality extraction by function fitting to time-series of satellite sensor data[J].Geoscience and Remote Sensing，IEEE Transactions on，2002，(40)：1824-1832.

[5]REED B C，BROWN J F，VANDER Z D，et al.Measuring phenological variability from satellite imagery[J].Journal of Vegetation Science，1994，(5)：703-714.

[6]DEFRIES R，TOWNSHEND J.Ndvi-derived land cover classifications at a global scale[J].International Journal of Remote Sensing，1994，(15)：3567-3586.

[7]LUNETTA R S，KNIGHT J F，EDIRIWICKREMA J，et al.Land-cover change detection using multi-temporal modisndvi data[J].Remote sensing of environment，2006，(105)：142-154.

[8]李儒，张霞，刘波，等.遥感时间序列数据滤波重建算法发展综述[J].遥感学报，2009，13(2)：335-341.

[9]MA M，VEROUSTRAETE F.Reconstructing pathfinder avhrr land ndvi time-series data for the northwest of China[J].Advances in Space Research，2006，(37：835-840.

[10]BRADLEY B A，JACOB R W，HERMANCE J F，et al.A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite ndvidata[J].Remote Sensing of Environment，2007，(106)：137-145.

[11]林忠辉，莫兴国.NDVI时间序列谐波分析与地表物候信息获取[J].农业工程学报，2006，22(12)：138-144.

[12]ZHU W，PAN Y，HE H，et al.A changing-weight filter method for reconstructing a high-quality ndvi time series to preserve the integrity of vegetation phenology[J].Geoscience and Remote Sensing，IEEE Transactions on，2012，(50)：1085-1094.

[13]吴文斌，杨鹏，唐华俊，等.两种NDVI时间序列数据拟合方法比较[J].农业工程学报，2009，25(11)：183-188.

[14]BECK P S，ATZBERGER C，HØGDA K A，et al.Improved monitoring of vegetation dynamics at very high latitudes：A new method using modisndvi[J].Remote sensing of Environment，2006，(100)：321-334.

[15]HIRD J N，MCDERMID G J.Noise reduction of ndvi time series：An empirical comparison of selected techniques[J].Remote Sensing of Environment，2009，(113)：248-258.

[16]CHEN J，JÖNSSON P，TAMURA M，et al.A simple method for reconstructing a high-quality ndvi time-series data set based on the savitzky-golayFilter[J].Remote sensing of Environment，2004，(91)：332-344.

[17]JULIEN Y，SOBRINO J A.Comparison of cloud-reconstruction methods for time series of composite ndvidata[J].Remote Sensing of Environment，2010，(114)：618-625.

[18]陈雪洋，蒙继华，杜鑫，等.基于环境星CCD数据的冬小麦叶面积指数遥感监测模型研究[J].国土资源遥感，2010，22(2)：55-58.

[19]孙志群，刘志辉，HJ-1 CCD影像大气校正模型比较研究[J].International Conference on Remote Sensing，2010，(3).

[20]JÖNSSON P，EKLUNDH L.Timesat—a program for analyzing time-series of satellite sensor data[J].Computers & Geosciences，2004，(30)：833-845.

[21]ROERINK G，MENENTI M，VERHOEF W.Reconstructing cloudfreendvi composites using fourier analysis of time series[J].International Journal of Remote Sensing，2000，(21)：1911-1917.

[22]李儒.遥感植被指数时间序列数据滤波重建算法研究[D].北京：中国科学院遥感应用研究所，2008.

[23]宋春桥，柯灵红，游松财，等.基于Timesat 的3种时序NDVI拟合方法比较研究—以藏北草地为例[J].遥感技术与应用，2011，26(2)：147-155.

[24]OLSSON L，EKLUNDH L.Fourier series for analysis of temporal sequences of satellite sensor imagery[J].International Journal of Remote Sensing，1994，(15)：3735-3741.

E-mail：yjs010@163.com