基于批量流水线调度问题的混合离散果蝇优化算法

潘玉霞+贾保先

摘要：提出了一种混合离散果蝇优化算法，求解以最大完工时间为目标的批量流水线调度问题。与传统的果蝇算法不同，首先，该算法采用基于工序的编码方式，使得算法适合解决调度问题；其次，混合了贪婪迭代进化机制进行群体间相互协作的学习，以此平衡算法的全局开发能力和局部搜索能力。仿真试验表明了所提果蝇算法的有效性和高效性。

关键词： 果蝇优化算法；批量流水线调度问题；贪婪迭代

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2015）30-0146-03

Hybrid Discrete Fruit Fly Optimization Algorithm for Lot-streaming Flow Shop Scheduling Problem

PAN Yu-xia1， JIA Bao-xian2

（1.Department of Basic Computer Education， Sanya University ，Sanya 572000，China；2.School of Computer Science，Liaocheng University， Liaocheng 252059，China ）

Abstract： This paper presents a Hybrid Discrete Fruit Fly Optimization Algorithm （HDFOA） for solving the Lot-streaming flow shop scheduling problem（LFSP） with makespan criteria.Unlike the traditional FOA， the proposed algorithm applies the job-permutation-based representation ，make sure it is suitable for scheduling problem. Second， Iterative Greedy is made for the whole group， so that the who group keeps in good balance between global exploration and local exploitation. Finally， to improve the efficiency of the scheduling algorithm . Computational results show that the FOA presented in this paper is very effective and efficient for the LFSP.

Key words： fruit fly optimization algorithm； lot-streaming flow shop scheduling problem； iterative greedy

1 概述

批量流水线调度问题（Lot-streaming Flowshop Scheduling Problem ，LFSP） 广泛应用于冶金、塑料、化工等工业生产中，具有重要的理论研究背景和实际应用价值。随着市场竞争的日益激烈和客户需求的多样化，多品种中小批量生产模式占据了主导地位。因此对批量流水线调度问题的研究已成为学术界和工程界的关注焦点。

果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）是近几年刚兴起的一类全局进化优化算法，于2011年由台湾博士潘文超提出的。该算法源于对果蝇觅食行为的模拟，已经在求解数学函数极值[3]，自动化仓库拣选作业调度问题[4]等方面得到成功的应用。由于FOA提出时间不长，理论研究尚不成熟，就已经在求解连续和离散问题方面显示了特有的优势。因此FOA算法的相关研究迫切需要开展。

2 批量流水线调度模型

为了减小机床的等待时间，将每个工件按等量分配的原则划分成若干个小批量。各个工件的小批量加工完成后就能被传送到下一台机床上加工，所有小批量的加工顺序都相同。假设工件按机床1到[m]的顺序加工，给定一个工序[π=δ1，δ2，…，δn]，工件[j]被划分成[sj]个小批量，[ltij]是工件[j]的小批量在机床[i]上的加工时间， [ctijk]为工件[j]的第[k]个小批量在机床[i]上的完成时间，[cj]为工件[j]的完成时间，则LFSP的数学模型为：

1）[ct1，δ1，1=lt1，δ1]

第一个工件的第一个小批量在第一台机床上的完成时间；

2）[cti，δ1，1=cti-1，δ1，1+lti，δ1]，[i=2，...，n]

第一个工件的第一个小批量在第[i]台机床上的完成时间；

3） [ct1，δ1，k=ct1，δ1，k-1+lt1，δ1] ，[k=2，...，sδj]

第一个工件的第[k]个小批量在第一台机床上的完成时间；

4） [ct1，δj，1=ct1，δj-1，sδj-1+lt1，δj]，[j=2，...，n]

第[j]个工件的第一个小批量在第一台机床上的完成时间；

5） [ct1，δj，k=ct1，δj，k-1+lt1，δj]，[j=2，...，n][k=2，...，sδj]

第[j]个工件的第[k]个小批量在第一台机床上的完成时间；

6） [cti，δj，k=maxcti-1，δj，k，cti，δj-1，sδj-1+lti，δj]，[k=1]

第[j]个工件的第一个小批量在第[i]台机床上的完成时间；

7） [cti，δj，k=maxcti-1，δj，k，cti，δj，k-1+lti，δj]，[k=2，...，sδj]

第[j]个工件的第[k]个小批量在在第[i]台机床上的完成时间；

调度的目标就是求最小化最大完工时间，即：

[minf（π）=cn=ctm，δn，sδn]

3 混合离散果蝇算法

果蝇优化算法的基本原理是初始化种群的中心位置，利用敏锐的嗅觉进行搜索，即根据中心位置随机产生多个邻域解。计算各可行解的味道浓度，即评价值，然后利用视觉从中选择较好的解，更新替换中心位置，然后进行迭代寻优，以更好的进靠近食物源。

FOA在整个迭代寻优过程中，所有个体都聚集到本次迭代的最优个体附近，只向当前最优果蝇个体学习，极易使算法陷入局部最优。要克服早熟的问题，必须提供一种机制可以跳出局部最优，在其他解空间中继续搜索[5]。此外，在连续空间中产生新个体的方法不适合解决调度。故运用FOA算法的主体流程，对其优化过程进行离散化是算法成功应用于LFSP的关键。基于以上分析，提出了混合离散果蝇算法（Hybrid Discrete Fruit Fly Optimization Algorithm ，HDFOA）。

3.1算法编码

对具有连续特性的算法进行离散化，首先要解决的关键问题是个体如何编码，即果蝇个体的表示方法。种群中的每个个体对应问题中的一个解，故采用基于工序的置换编码，因为基于工序的置换编码承载与问题相关的必要信息，已经广泛应用于此类文章中[6]。

以5工件调度问题为例，在（-1，1）之间产生5个随机数（-0.4，0.6，0.3，0.5，-0.1，0.0），利用最大位置值规则得到一个置换解（2，4，3，6，5，1）。

3.2种群初始化

FOA算法基本思想是在种群的初始位置基础上，向食物源飞近，因此，好的初始解有利于提高算法的收敛速度和解的质量。一个好的初始解应该以较大的概率覆盖解空间，并包含部分质量高的个体以指导算法搜索方向。为了保证种群中初始解的多样性和高质量，初始解在解空间中随机产生。初始化方法如下：

[x={-0.6，-0.5，0.1，0.2，-0.1，0.3}]，利用最大位置法将和声解转化成工序[π={6，4，3，5，2，1}]。

a） 嗅觉和视觉搜索

影响FOA算法性能的核心是如何生成嗅觉阶段的邻域个体[6]。本文结合迭代贪婪（Iterative Greedy，IG）进化过程，对种群中的果蝇个体进行优化，迭代贪婪启发式算法步骤如下：

步骤1：分解当前个体

1） 从当前个体中随机取出[d]个工件，标记为[πR]，其中[d]为工件数范围内随机产生的整数。

2） 剩余的n-d个工件组成果蝇个体的一部分，标记给[πD]

步骤2：利用NEH方法的最后一步组成新的果蝇个体

1） 设置参数[i=1]

2） [πR]中的第[i]个工件被重新插入到[πD]的[n-d+i]个可能的位置，选出目标值最好的解作为当前解。

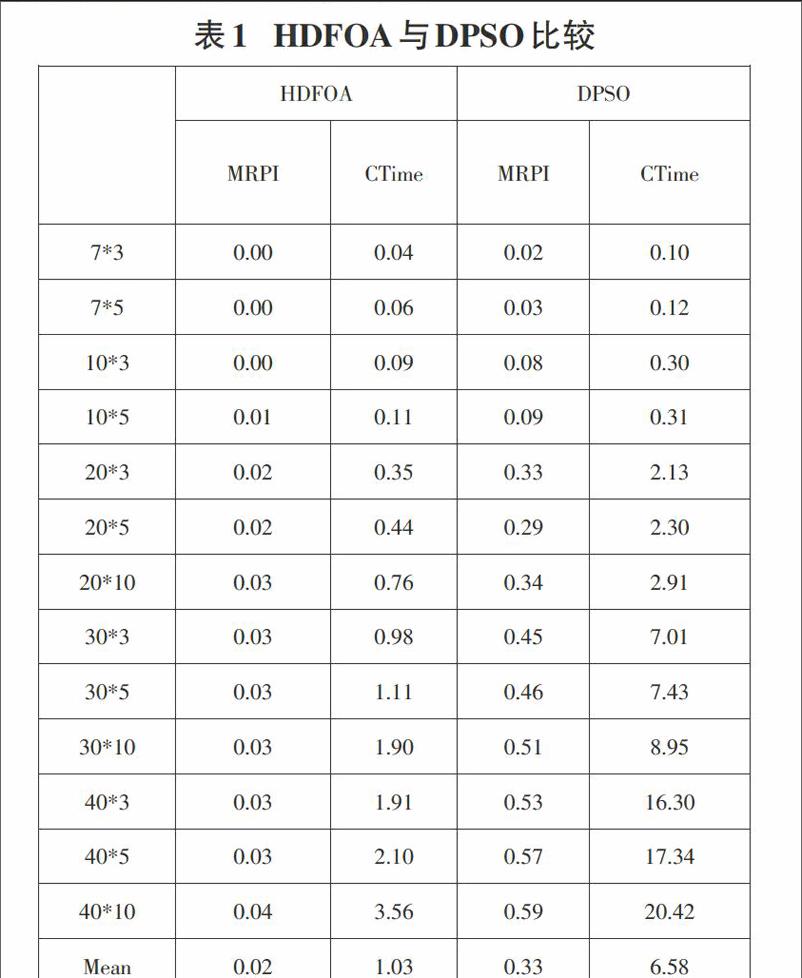
3） [i=i+1]，[i

利用视觉功能确定新解是否优于当前解，若是，则更新当前解。

4 HDFOA算法流程

基于以上分析，混合离散果蝇优化算法步骤如下

步骤1：初始化参数，种群个体数，迭代代数

步骤2：初始化果蝇个体。

步骤3：利用IG进化过程产生新果蝇个体

步骤4：更新种群。利用视觉选择决定是否更新解。如果新果蝇个体比较好，则替换之，否则不变。

5 仿真实验

通过与文献[7]提出的DPSO算法进行比较，测试本文提出的算法的性能。采用与文献[7]相同的参数设置和指标。利用C++编程语言，在处理器为Intel（R）Core（TM） i3 2GHZ、内存为2.00G的PC机上进行程序测试。为了公平比较，各算法采用相同的终止条件，每个实例独立运行30次。

两种算法比较结果如表1所示

由表1知：

1） HDFOA的平均MRPI为0.02，远远小于DPSO的0.33，说明了HDFOA具有较好的求解质量。

2） HDFOA的平均时间为1.03，远远小于DPSO的6.58，说明了HDFOA具有较快的收敛速度。

3） 13个不同规模的问题来看，随着问题规模的增加，HDFOA的优越性越来越明显。

总之，与DPSO相比，HDFOA具有较优越的性能。

6 总结

结合LFSP的特点，设计了工序编码的混合离散果蝇调度算法。为了克服果蝇算法容易陷入局部最优的缺陷，在框架中引入基于IG的进化方案。仿真结果表明所得算法具有较高的优化性能。

参考文献：

[1] 周亚勤，李蓓智，杨建国.基于遗传算法的批量Flow-shop调度问题研究，机械制造[J].2004，42（482）：57-59.

[2] Tseng C T，Liao C J.A discrete particle swarm optimization for lot-streaming flowshop scheduling problem[J].European Journal of Operational Research，2007，8（30）.

[3] 潘文超.果蝇最佳化演算法[M].台北： 沧海书局，2011： 10-12.

[4] 刘志雄，王雅芬，张煜.多种群果蝇优化算法求解自动化仓库拣选作业调度问题[J].武汉理工大学学报，2014，36（3）.

[5] 韩俊英，刘成忠，王联国.动态双子群协同进化果蝇优化算法[J].模式识别与人工智能，2013（11）：1057-1067.

[6] 郑晓龙，王凌，王圣尧.求解置换流水线调度问题的混合离散果蝇算法[J].控制理论与应用， 2014， 31（2）： 159 -164.

[7] 潘玉霞，潘全科，桑红燕，武磊.解决批量流水线调度问题的离散微粒群算法[J].聊城大学学报， 22（3）.