具有丢包的异采样率双环网络控制系统

梁澄河，刘电霆(桂林理工大学机械与控制工程学院，广西桂林　541004)



具有丢包的异采样率双环网络控制系统

梁澄河，刘电霆
(桂林理工大学机械与控制工程学院，广西桂林541004)

摘要:研究了一类存在数据包丢失的异采样率双环网络控制系统。该系统由内控制环和外控制环组成，内、外控制环的采样周期不同，且由于网络的存在，传输过程会出现数据包丢失问题。采用提升技术将内环扩展成多采样周期模型来解决内环和外环统一建模的问题，利用马尔可夫链来描述数据包丢失情况，并建立综合系统模型。基于李雅普诺夫方法，给出了网络控制系统随机稳定的充分条件，提出控制器的设计方法，并通过数值算例验证了方法的有效性。

关键词:网络控制系统;异采样率;马尔可夫链;数据包丢失

网络控制系统( networked control systems，NCSs)正越来越广泛应用于工业中［1］。异采样率双环NCSs是一种新模型，反映了生产中控制系统具有双环结构且被控量变化速率不同的问题，如电机具有电流环和转速环。双环模型、采样周期不同步和网络时延丢包是异采样率双环NCSs的特点。

目前对于NCSs控制的研究主要集中在单环系统和串级控制系统的建模、稳定性分析、保性能问题和控制器设计方面，对于异采样率NCSs的研究还很少。文献［2－5］研究了具有数据包丢失的单环NCSs建模问题;文献［6－10］分析了多输入输出NCSs建模并推导了保性能稳定条件;文献［11－12］讨论了网络化串级控制系统稳定性问题。由于常规NCSs方法难以适用于异采样率双环NCSs，因此有必要对此进行特别分析。

笔者研究了异采样率双环NCSs建模和稳定性，利用提升技术对内环和外环统一建模、马尔可夫链描述网络节点丢包，采用Lyapunov方法得出随机稳定的充分条件。

1　网络控制系统建模

异采样率双环NCSs结构如图1所示。系统包括被控对象(分解为被控对象1和被控对象2，两者为串联)、2个传感器、2个控制器和1个执行器。内控制环由被控对象1、传感器1、控制器1和执行器组成，外控制环由被控对象1、被控对象2、传感器2、控制器2、控制器1和执行器组成。考虑以下连续时间NCSs模型:

被控对象1

其中:被控对象1状态xp1( t)∈Rn;被控对象1输入up1( t)∈Rm;被控对象1输出yp1( t)∈R; A1，B1，C1是系数矩阵。

被控对象2

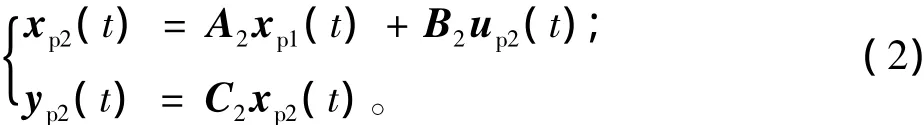
其中:被控对象2状态xp2( t)∈Rn;被控对象2输入up2( t)∈Rm;被控对象2输出yp2( t)∈Rp; A2，B2，C2是系数矩阵。

假设传感器节点为时间驱动，控制器和执行器为事件驱动。内环采样周期为T1，外环采样周期T2，T1＜T2。各个节点间的网络诱导时延是时变不确定的，分别表示为τca、τsc1、τss、τsc2，令τ1=τca+τsc1、τ2= τca+τss+τsc2，且均小于内环采样周期T1。数据采用单包传输，传输过程存在数据包丢失问题，丢包符合马尔可夫链过程。

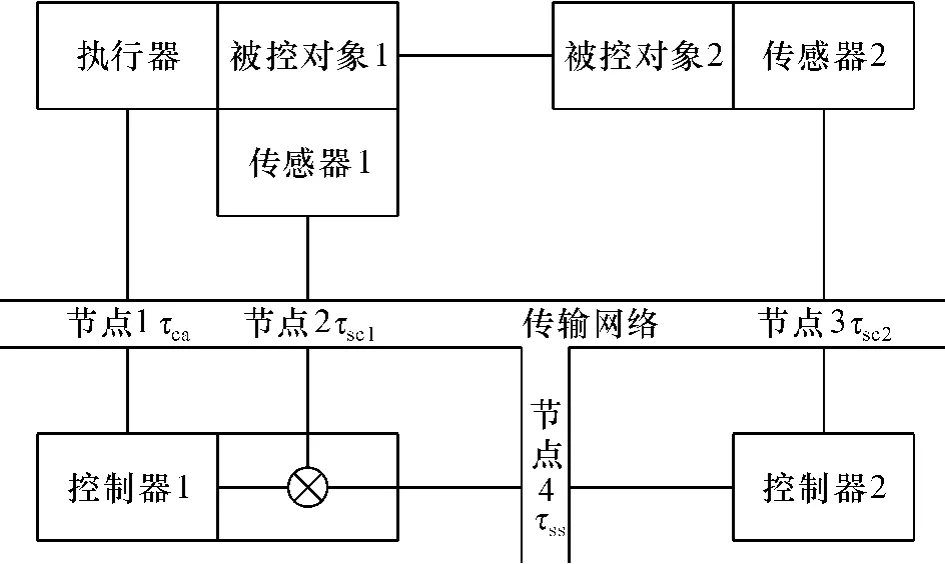
图1　异采样率双环网络控制系统Fig. 61Double-loop network control system in different sampling periods

在此只考虑系统的内外环采样周期成整数倍关系的情况，即T2= mT1( m为正整数)。在T2≠mT1或T1＞T2时，同理。

离散NCSs模型( 1)和( 2)，有

被控对象1:

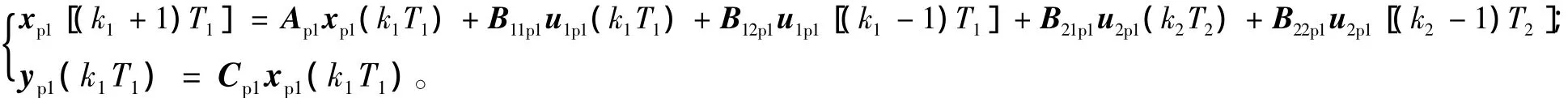
被控对象2:

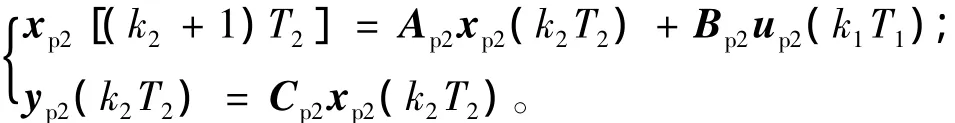
系统内环和外环存在T2= mT1的关系，直接建立模型难以说明内外环采样周期不同的特点，故采用提升技术，将内环采样周期T1选定为基本周期，以单位外环采样周期T2为大周期，将内环变量处理成多周期采样系统(图2)。m不为正整数，亦可以采用提升技术，只需将T1和T2的最小公约数选定为基本周期即可。

采用提升技术扩展变量，包括内环状态量和被控对象2输入量:

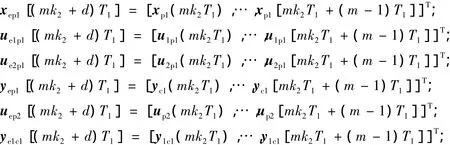
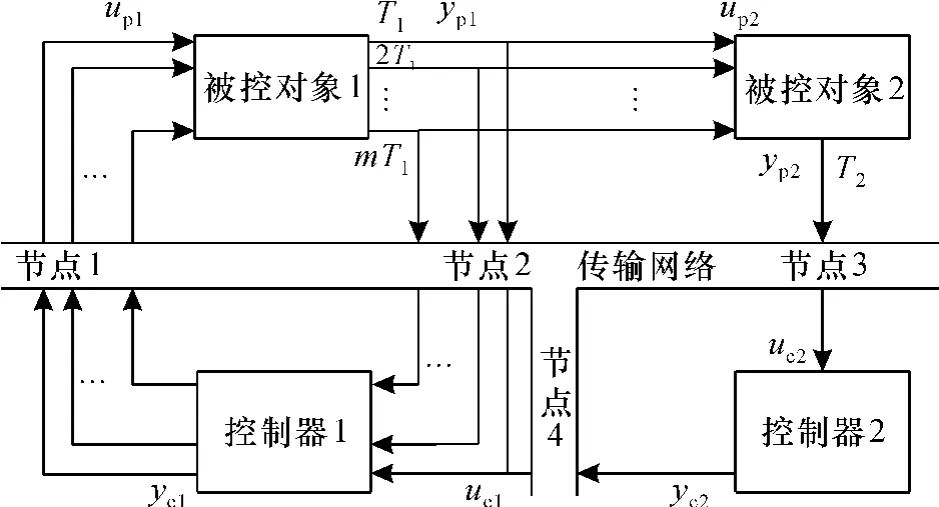
图2　采用提升技术的系统示意图Fig. 62Lifting technology of schematic diagram

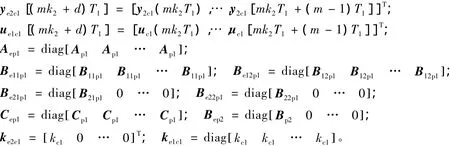
对角阵M( k1)和Λ( k1)表示控制器1与执行器和传感器1的网络通信情况;引入Π( k1)和Δ( k1)表示控制器2与控制器1和传感器1的网络通信状况。采用δt分别表示网络节点t的通信成功情况，假设函数δt( k)是取值为0或1的马尔可夫链，且相互独立，当δt( k) = 0时，说明网络发生数据信号丢失，则有下述关系:

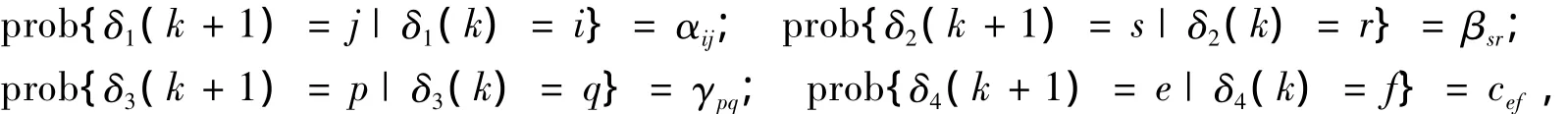
1，则M( k1)，Λ( k1)，Π( k1)和Δ( k1)分别为

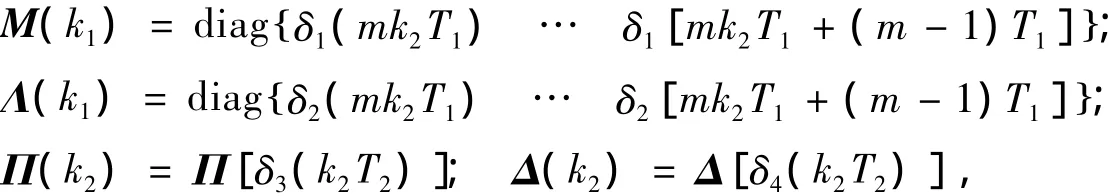
其中:矩阵M( k1)中每一个变量都由前一周期的转移概率决定，则矩阵M( k1)马尔可夫链的状态转移概率仍为

prob{ M( k1+ 1) | M( k1) } =αij。

同理可知prob{Λ( k1+ 1) |Λ( k1) } =βsr。令M = M( k1)，Λ=Λ( k1)，Π=Π( k1)，Δ=Δ( k1)且考虑数据包丢失，被控对象和控制器输入为

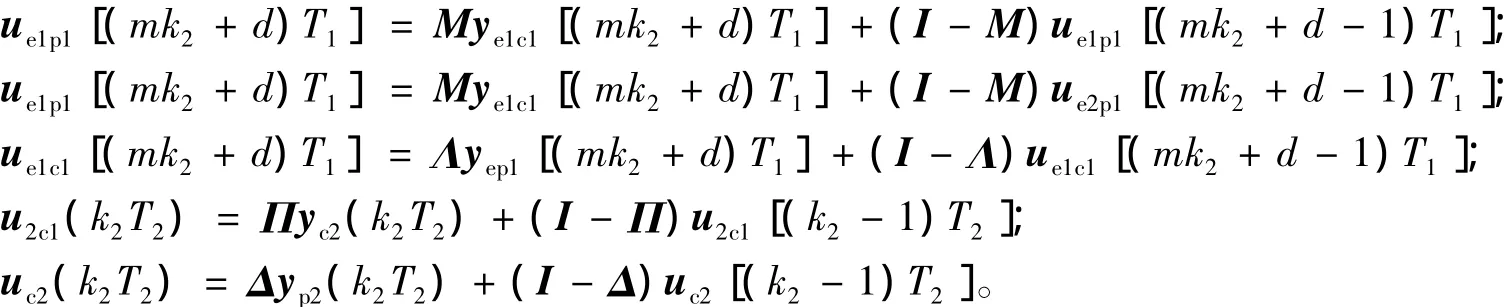
设系统状态增广量可以表示为

z( k) =［xep1xp2ue1p1ue2p1ue1c1u2c1uc2］T，

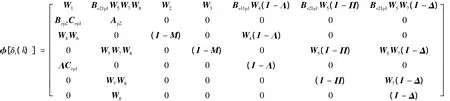
其中:且W1= Aep1+ Be11p1W4W6; W2= Be11p1( I－M) + Be12p1; W3= Be21p1( I－M) + Be22p1; W4= Mke1c1; W5= Mke2c1; W6=ΛCep1; W7=Πkc2; W8=ΔCp2。

2　稳定性分析

引理1［13］( Schur补定理)给定常数矩阵A，P，Q，其中Q = QT，PT= P＞0，则ATPA + Q＜0成立，当且仅当

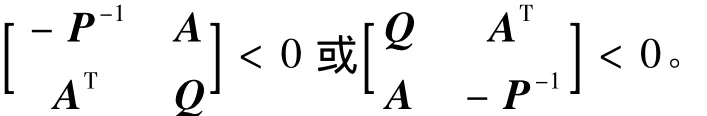
定理1如果存在正定矩阵P［δ1( k)，δ2( k)，δ3( k)，δ4( k)］使下式成立:

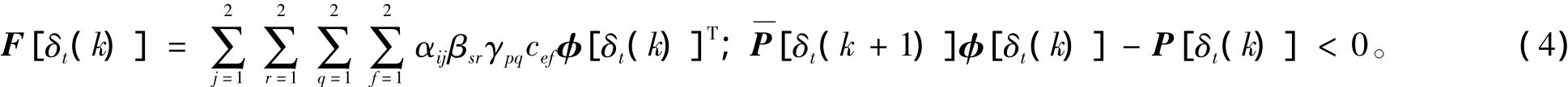
其中:

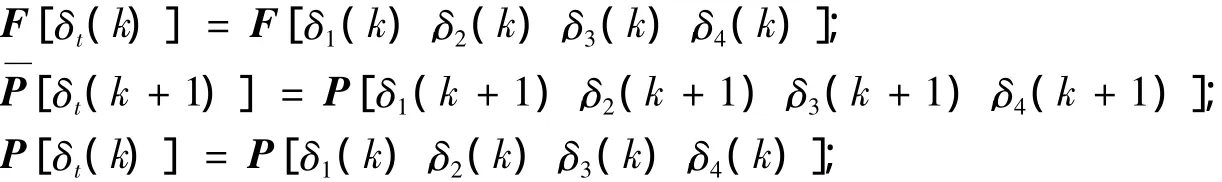
则闭环系统( 3)是随机稳定的。

证明构造李雅普诺夫函数: V［z( k)］= z( k)TP［δt( k)］z［( k)］，

其中，P［δt( k)］是待定正定矩阵。

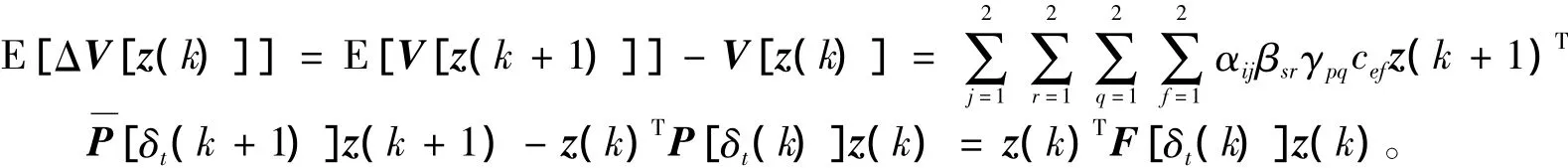
其中，

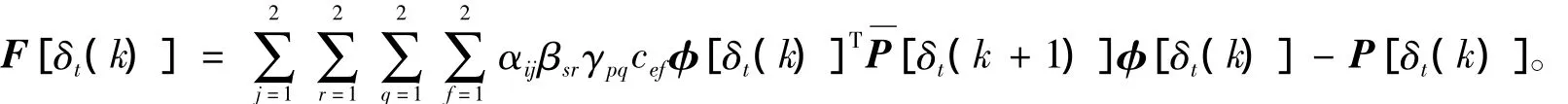
如果F［δt( k)］＜0，则有

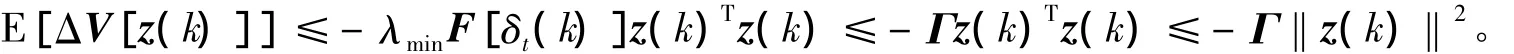
其中，Γ=－λmin{ F［δt( k)］}＞0，则当T≥1时，

故闭环系统是随机稳定的。

3　控制器设计

利用Schur引理，式( 4)可等价于

其中: Nd=［N1…Ni］; P = P(δt( k) ) ;

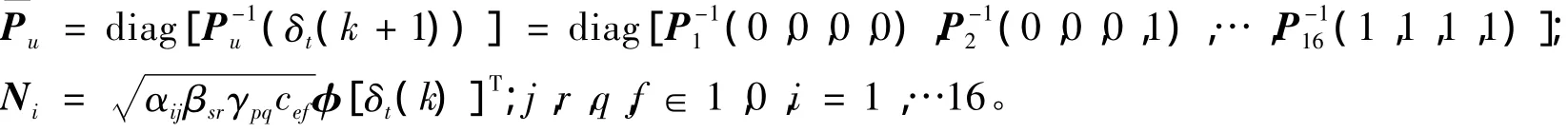
参考文献［9］，利用锥补线性化算法，记矩阵( 5)为Ψ［δt( k)］，用Ω［δt( k)］记作矩阵中的+ 1)］，则优化问题为

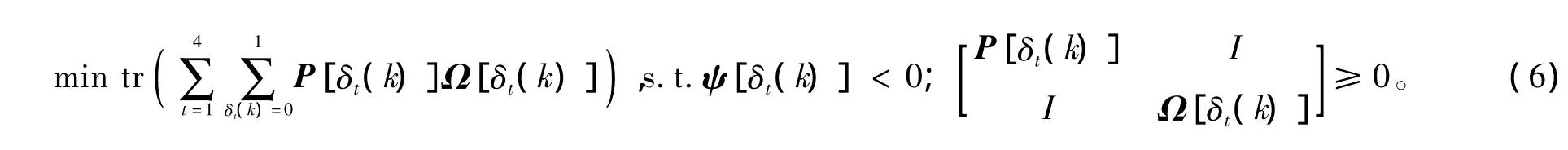
优化问题通过迭代算法求解:

(ⅰ)由式( 1)解出式( 6)的一组可行解P0［δt( k)］，Ω0［δt( k)］和K0，迭代次数j = 0;

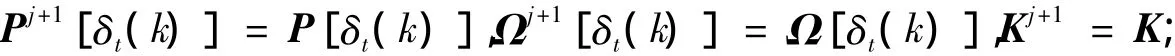
(ⅲ)若P［δt( k)］符合式( 5)，则停止，得到可行解。否则令j = j + 1，重复上述步骤。

4　仿真实例

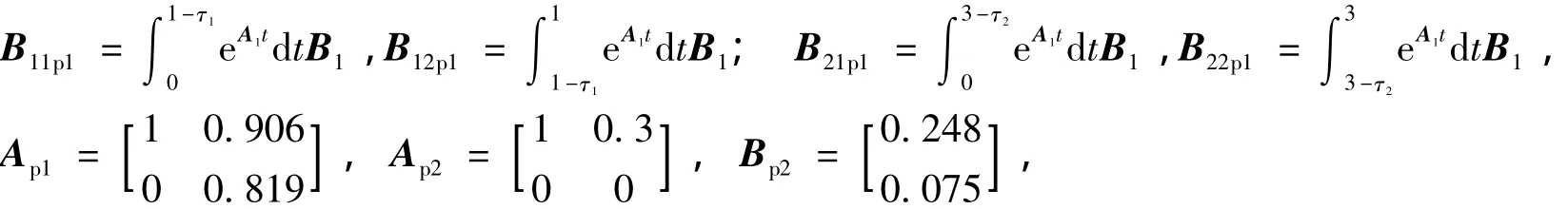
离散化后系统模型为τ1和τ2为内环网络时延和外环网络时延。

仿真时间为200 s，内环采样周期为1 s，外环采样周期为3 s，网络丢包率为0. 2，系统初始值为［2－0. 5］。由锥补线性化法，得控制器增益矩阵参数为kc1=－0. 19，kc2= 0. 35。

对比采用文献［14］中的鲁棒控制器设计方法计算异采样率双环NCSs控制器，则增益矩阵参数为kzc1=－0. 2，kzc2= 0. 12。

对比图3、图4和图5、图6 (图中Y1、Y2分别是控制系统中被控对象1、2的输出)，可以发现鲁棒控制器设计难以适用于异采样率双环NCSs，系统达到稳定的时间更久，且波动幅度更大，而锥补线性化法设计控制器效果更优。证明了文中对异采样率双环NCSs的建模、稳定性分析和锥补线性化法设计控制器是正确的。

5　结论

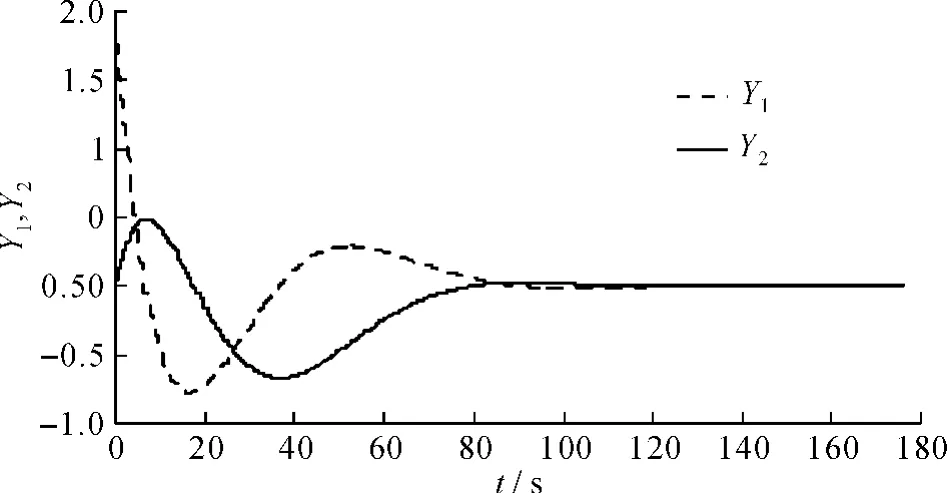
图3　时延为0.5s的系统输出曲线Fig. 63Output curve at 0.5s delay time

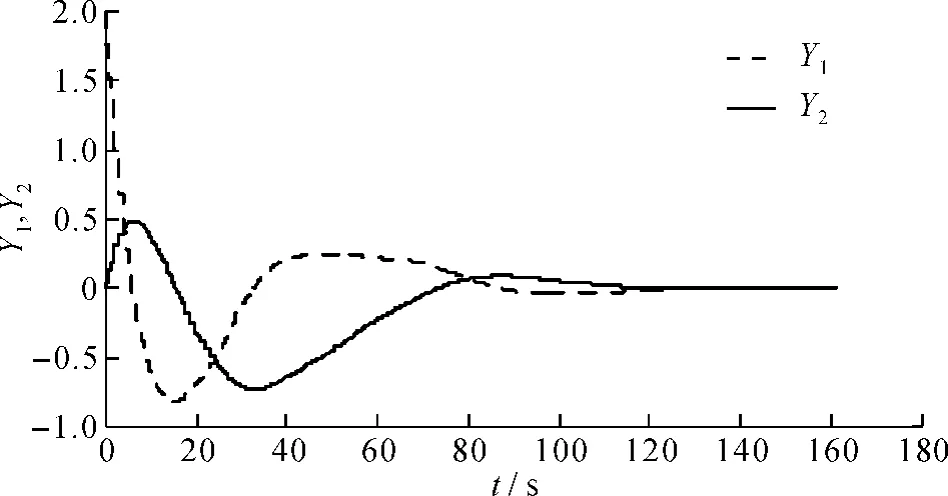
图4　时延为0.5s存在丢包的系统输出曲线Fig. 64Output curve of packet dropout system at 0.5 s

讨论了存在数据包丢失的异采样率双环NCSs建模和控制器设计问题。将异采样周期系统内环建模成多采样周期模型，使系统变量统一到单位外环采样周期内，并利用马尔可夫链描述数据包丢失，综合建立状态增广矩阵。利用李亚谱诺夫理论给出系统的随机稳定充分条件，设计了控制器，并以实例来证明方法的有效性。

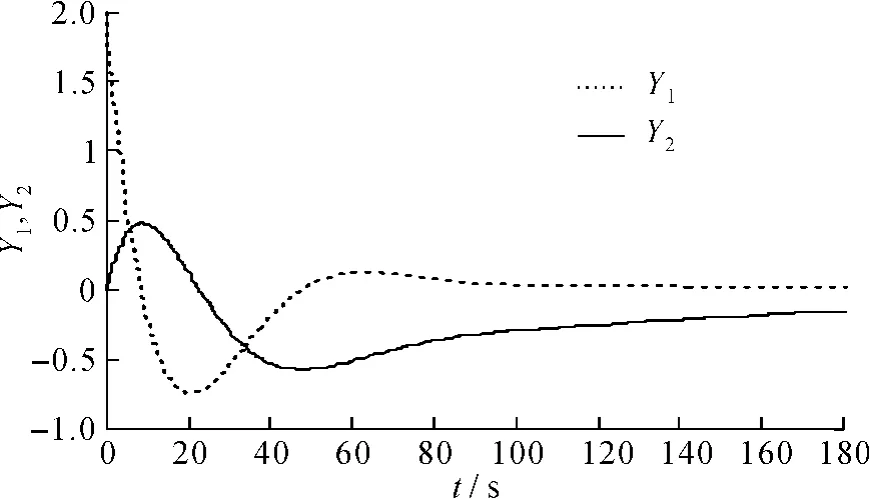
图5　时延0.5s鲁棒控制器的输出曲线Fig. 65Output curve of robust controller at 0.5 s delay time

［1］Zhang W，Branicky M S，Stephen M P．Stability of networked control systems［J］．IEEE Control Systems Magazine，2001，21 ( 1) : 84－99．

［2］Yang F，Fang H J．Control structure design of networked control systems based on maximum allowable delay bounds［J］．Journal of the Franklin Institute，2009，346 ( 6) : 626－635．

［3］Zhang W A，Li Y．Modeling and control of networked control systems with both network-induced delay and packet dropout ［J］．Automatica，2008，44 ( 12) : 3206－3210．

［4］Li J N，Zhang Q L，Yu H B，et al．Real-time guaranteed cost control of MIMO networked control systems with packet disordering［J］．Journal of Process Control，2011，21 ( 6) : 967－975．

［5］朱进，王林鹏．转移概率未知下具有双Markov链的网络控制系统控制器设计［J］．控制与决策，2013，28 ( 4) : 489－494．

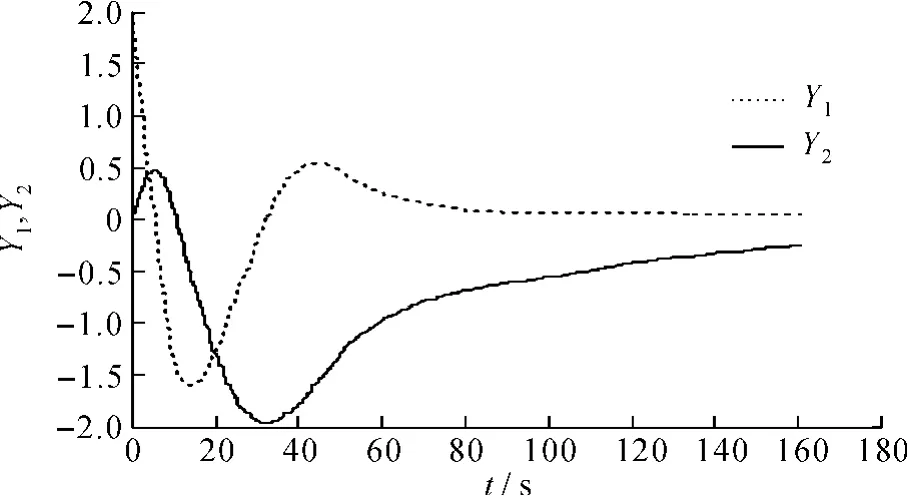
图6　时延0.5s鲁棒控制器有丢包的输出曲线Fig. 66Output curve of packet dropout robust controller at 0.5 s delay time

［6］孙文安，丁卜琳，邵洪艳，等．一类不确定网络控制系统的鲁棒H∞控制［J］．计算技术与自动化，2013，32 ( 1) : 6－10．

［7］谢德晓，张登峰，韩笑冬，等．一类不确定网络控制系统的鲁棒容错控制［J］．信息与控制，2010，39( 4) :472－478．

［8］刘电霆，陈小雄．一类多时延网络控制系统的稳定性分析和鲁棒H∞控制［J］．桂林理工大学学报，2014，34 ( 1) : 151－162．

［9］Chen W，Qiu L．Stabilization of network control systems with multi-rate sampling［J］．Automatica，2013，49( 6) :1528－1537．

［10］van Loon S J L M，Donkers M C F，van de Wouw N，et al．Stability analysis of networked and quantized linear control systems［J］．Nonlinear Analysis: Hybrid Systems，2013，10: 111－125．

［11］会国涛，王迎春，张化光．具有随机时延的网络控制系统周期反馈控制［J］．控制与决策，2013，28 ( 5) : 706－710．

［12］陆仲达，田群宏，王俊科，等．网络控制系统H∞鲁棒控制器设计［J］．计算机应用研究，2014，31 ( 2) : 472－475．

［13］陈青，吴敏．具有网络丢包和时延的网络控制系统设计［J］．控制与决策，2011，26 ( 2) : 293－296．

［14］严怀成，苏阵阵，张皓，等．具有时变时滞和多包丢失的网络控制系统量化H∞控制［J］．控制理论与应用，2013，30 ( 4) : 469－474．

Double-loop network control system
in different sampling periods and data packet dropout

LIANG Cheng-he，LIU Dian-ting
( College of Mechanical and Control Engineering，Guilin University of Technology，Guilin 541004，China)

Abstract:A class of multi-rate double-loop network control system is studied．The system is composed of innerloop and outer-loop with different sampling periods and packet loss．In the paper，the inner loop was extended to multi-sampling cycle model by lifting technology to solve the problem of unified modeling of the inner-loop and outer-loop．Then Markov chain is used to describe the packet loss process by lifting technology．Based on the method of Lyapunov，sufficient conditions for stochastic stability of network control systems are given．The controller design method is discussed．Finally，numerical examples are studied to verify the effectiveness of the proposed method．

Key words:network control system; differential sampling rate; Markov; packet dropout

通讯作者:刘电霆，博士，教授，liudian@163. com。

作者简介:梁澄河( 1988—)，男，硕士研究生，研究方向:检测技术与自动化装置，lch5639355@163. com。

基金项目:广西高校优秀人才项目(桂教人［2009］62) ;广西汽车零部件与整车技术重点实验室项目( 2013KFMS03) ;广西高校重点科研项目( 201202ZD048) ;广西研究生教育创新计划项目( YCSZ2014153)

收稿日期:2013－03－13

doi:10. 3969/j．issn. 1674－9057. 2015. 01. 034

文章编号:1674－9057( 2015) 01－0207－06

文献标志码:A

中图分类号:TP273

引文格式:梁澄河，刘电霆．具有丢包的异采样率双环网络控制系统［J］．桂林理工大学学报，2015，35 ( 1) : 207－212．