中国上市银行效率与全要素生产率再研究——基于两阶段网络方向性距离SBM模型的实证分析

李小胜，张焕明

(安徽财经大学 统计与应用数学学院，安徽 蚌埠233030)

中国上市银行效率与全要素生产率再研究
——基于两阶段网络方向性距离SBM模型的实证分析

李小胜，张焕明

(安徽财经大学 统计与应用数学学院，安徽 蚌埠233030)

摘要：现有文献运用数据包络分析模型对银行业的效率进行了大量的实证研究，但是大多没有考虑银行业效率评价的网络结构，也较少考虑银行业的非期望产出，从而其估计结果颇受质疑。文章利用中国16家上市银行2004-2012年的数据，将银行业的生产看成是一个两阶段网络生产过程，并考虑了银行业的不良贷款作为非期望产出时的弱可处置性问题，运用两阶段网络方向性距离松弛的数据包络模型进行了系统的测量研究。分析表明，国有银行的效率仍然偏低，各家银行都存在非效率现象，但效率变化呈现出一种倒U形变化的趋势，尤其是近几年银行业的效率有显著提高；银行业效率评价方法的选择对实证结果非常重要，未考虑与考虑松弛作用时的估计结果有很大差异。全要素生产率的分析结果表明，银行业的整体业绩变好，这是技术进步和技术效率提升共同作用的结果，主要得益于2003年以来推行的国有银行股份制改造和公开上市所产生的硬约束效应。文章进一步分析了影响银行业非效率的因素，结果表明宏观经济因素对银行业效率的影响并不明显，银行业内部因素对非效率项的影响显著。

关键词：两阶段网络DEA；方向性距离；上市银行效率

张焕明(1973-)，男，湖北襄樊人，安徽财经大学统计与应用数学学院教授。

一、引言

银行业作为重要的金融中介，对一个国家的经济发展和资源配置起着重要的作用。从中国人民银行网站公布的社会融资规模来看，2013年10月份通过银行融资的比重占到90%以上。银行业是我国目前融资的主要渠道，在这种间接融资成为当前我国资源配置主要渠道的情况下，银行业效率的高低直接关系到整个行业的利润以及宏观效率的高低(蔡跃洲和郭梅军，2009)。Fujii等(2014)认为，宏观上银行业效率的提升能够降低金融中介的成本和促进整个金融体系的稳定，也能促进金融资源的合理配置，从而带动经济增长；微观上随着金融业的发展，竞争日益激烈，效率分析也可促使银行完善制度建设、提升监管能力。

截至2012年底，从市价总值看，中国四大国有商业银行位列世界银行业的前十名，特别是中国工商银行和中国建设银行按照市价总值分别位列第一和第二。近年来受人民币汇率升值影响，原材料价格和工资成本上升，多数上市公司的投资收益呈下降的趋势，但是我国16家上市银行的利润却占所有上市公司利润的53.6%左右，达到1.03万亿元人民币。经过不良资产的剥离和贷款的严格审批程序，银行业的利润有了大幅的提高。如果根据利润来判断银行业的业绩好坏，那么中国银行业的效率很高，经营效果较好。但从单一指标来评价银行业的效率明显存在缺陷，如我国银行业目前仍存在大量的不良贷款、贷款和存款的比例不协调、银行惜贷比较严重等。因此，根据银行业经营的多投入和多产出特点，不仅要考虑期望产出，也要考虑非期望产出；不仅要与自身历年经营业绩比较，也要与行业中优秀的银行比较。那么在考虑这些因素之后，我国上市银行的效率如何，影响因素有哪些，各家银行是否有改进的余地，银行业全要素生产率的增长情况如何，这些成为本文关注的焦点。

对银行业的效率评价由来已久，国内外积累了大量的文献。从某种意义上说，对银行的效率评价是许多新的数量经济分析方法的“试验田”。这说明了银行效率评价的重要性，也表明评价方法是否合理会导致评价结果相差很大。本文在对这些方法进行述评的基础上，将应用一种比较稳健的两阶段网络方向性距离松弛的数据包络模型(two-stagenetworkdirectionaldistanceslacks-basedinefficiencymodel)对上市银行效率进行评价。本文的研究能够为银行业效率改进和投资者投资决策提供参考依据，也能为后续的研究提供新的实证研究方法。

二、文献综述

Berger和Humphrey(1997)对银行业的效率评价进行了系统的文献综述，认为实证研究中主要采用的是参数方法和非参数方法。参数方法包括随机前沿分析法(stochasticfrontierapproach，SFA)、厚前沿分析法(thickfrontierapproach，TFA)和自由分布分析法(distributionfreeapproach，DFA)，而实际中随机前沿分析法应用较多。非参数方法包括数据包络分析(DEA)和自由处置壳(freedisposalhull，FDH)等方法，而实证研究中以DEA方法居多。Fethi和Pasiouras(2010)认为，虽然两种方法各有优势和缺点，但是相对而言，DEA方法的应用更为广泛，对于银行效率的评价具有比较优势。

数据包络分析方法通过构造分段的前沿面，不需要设定具体的函数形式，而且能够处理多投入和多产出的情况，在银行业效率评价中逐渐受到人们的青睐。例如，Sherman和Gold(1985)就采用DEA模型对美国商业银行分支机构的效率进行了评价，得到平均的效率为0.96。随后出现了大量的评价文献，Berg等(1993)采用该方法对挪威、瑞典、芬兰三国的银行业效率进行了评价，得到的效率值分别为0.57、0.78和0.53。Isik和Hassan(2002)对土耳其的银行业效率进行了评价，得到的效率值为0.82。国内学者薛峰和杨德礼(1998)同样采用DEA方法对中国银行业的效率进行了评价，张健华(2003)对1997-2001年中国三类银行的效率进行了评价和排名。蔡跃洲和郭梅军(2009)对2004-2008年中国11家上市银行进行了效率评价，并对全要素生产率进行了分析。

然而，上述运用传统DEA方法进行效率评价的文献存在很多不足。首先，以往的DEA模型对决策单元效率的估计采用的是径向(Radial)的方法，这种方法在存在松弛情况下会高估决策单元的效率(Fukuyama和Weber，2009)；其次，上述文献通常没有考虑不良贷款，从而会导致评价结果存在偏差(王兵和朱宁，2011)。针对第一个问题，Charnes等(1985)提出了一种加性模型，这种模型最大化投入松弛和产出松弛，但它不是真正意义上的效率测量模型，因为目标函数中的投入松弛和产出松弛的单位通常不一致。针对加性模型中投入松弛和产出松弛加总过程中单位不一致的问题，Färe等(1985)提出了Russell测度的方法，Cooper等(2011)及Tone(2001)则提出了SBM(slacks-basedmodel)方法。这些方法将目标函数中的投入松弛和产出松弛进行了标准化，使目标函数中的投入松弛和产出松弛成为无量纲的量，这样加总就得到真正意义上的效率值。这种评价效率的模型又分为投入导向、产出导向和非导向的形式，其中非导向形式的应用较广，它可以避免导向选择所引起的效率评价结果偏差。

上述模型即使得到了改进，其在经济应用中还是与生产过程中的利润最大化目标产生不一致。Chambers等(1996)从方向性距离函数的观点出发，提出了非效率的度量方法。方向性距离函数寻求给定方向下非径向的产出扩张和非径向的投入缩减最大化。方向性距离函数是利润函数的对偶形式，具有良好的性质。由于经济生产活动在某种程度上是追求利润最大化的过程，方向性距离函数被很多文献所采用，如Chung等(1997)及Färe等(2007)成功地将方向性距离函数应用于环境效率评价中。但是方向性距离函数还是没有很好地解决投入、产出松弛问题，而且本质上还是一种径向的调整模型。针对方向性距离函数的上述问题，Fukuyama和Weber(2009)提出了基于松弛测度的非径向、非导向的方向性距离函数，并对日本银行业的效率进行了评价。在上述思想下，国内学者王兵和朱宁(2011)在不良贷款约束下运用SBM方向性距离函数测度了2003-2009年我国11 家上市商业银行的效率。柯孔林和冯宗宪(2008)运用方向性距离函数对2000-2005年中国银行业效率进行了评价。

不过，上述文献只考虑了投入和产出过程，而没有考虑投入和产出之间的连接，将生产过程看成是“黑箱”。其实很多生产过程具有网络结构，若忽略会导致估计得到的效率值偏高。Seiford和Zhu(1999)较早注意到银行业生产过程的两阶段网络结构的特征，并运用独立的两阶段数据包络分析方法对美国的银行业效率进行了评价。他们将两个阶段看成是独立的生产过程，而实际上第一阶段的产出作为中间产品是下一阶段的投入，根据效率评价的规则应该尽量少，而作为第一阶段的产出应该尽量多，所以这两个阶段的效率评价是相互联系的。Kao和Hwang(2008)提出整个过程的效率是这两个阶段效率的乘积，并应用在中国台湾的非寿险业效率评价中。Chen等(2009)认为，整个过程的效率是这两个阶段效率的相加。Liang 等(2008)从斯塔克伯格博弈的观点解决了两个阶段效率评价的问题。Fukuyama和Weber(2009)将两个生产过程放在一个框架中，得到两个阶段的一个综合效率。

为了弥补上述研究文献的不足，本文在借鉴国际最前沿处理方法的基础上，采用两阶段网络方向性距离松弛的数据包络模型对2004-2012年中国16家上市银行的效率进行了评价，获得了比以往研究更为准确、可靠的分析结论，拓展了该领域的研究。本文的贡献主要体现在以下三个方面：首先，从银行业生产的网络结构出发，将生产过程看成一个相互联系的两阶段生产过程，避免了以往将银行业生产过程看成“黑箱”而导致评价效率不合理的情况出现。其次，考虑到以往径向调整高估效率的问题，本文加入了投入和产出松弛，并选择非导向效率评价模型，在方向性距离函数的基础上对目标函数中的松弛进行了标准化，使其成为真正的效率评价值，并构造了跨期的效率测量模型和全要素生产率指数。最后，本文将不良贷款作为非期望产出，并认为银行每一期的第二阶段非期望产出会成为下一期的第一阶段投入，影响下一期的存款吸收。

三、方法介绍

(一)银行业效率测量方法介绍

根据Seiford和Zhu(1999)的思想，本文认为银行业的生产过程具有两阶段网络结构特征，具体表现为：银行通过固定资产净值、股权资本和人员等初始的投入吸收存款，产生负债业务，这是银行经营的第一个阶段，也是开展业务的基础。很多银行都对存款业务非常重视，常以存款的多少作为考核员工的主要指标，对这个阶段的效率非常关注。而银行组织存款的目的是产生生息资产、获得利润，近年来很多银行的投资和贷款失败，给其带来严重的损失，所以在完成第一个阶段的生产后银行会考虑投资组合，包括贷款对象的甄别以及投资品种的选择。这个阶段主要是运用资金的阶段，如果这个阶段的效率不高，同样会导致银行的效率降低。这两个阶段中任何一个阶段的无效率都会导致银行的整体无效率。传统的研究中忽视了银行中间产品的生产过程，将存款看成产出或者投入，把银行业的经营过程看成一个单一阶段的生产过程。这样处理既不符合效率评价原理，也不符合银行业经营的现实。在单一阶段效率评价中，将存款看成产出还是投入，很多观点是不一致的；而两阶段的生产过程能够有效避免划分的问题(Holod和Lewis，2011)，将其看成中间产品，为正确评价银行业的效率提供了合理的途径，也为揭开银行业经营的“黑箱”提供了依据。

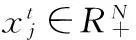
(1)

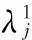
对于没有考虑松弛作用的两阶段网络方向性距离函数模型，我们可以用下式表示：

(2)

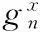
上述的两阶段网络方向性距离函数模型没有考虑松弛问题，会导致评价结果偏高。为了克服这个问题，我们采用Akther等(2013)的模型进行效率测量，具体的设定如下：

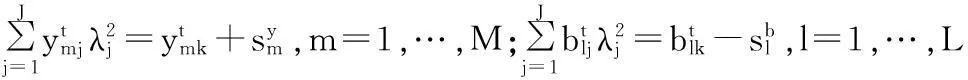
(3)

(4)

(二)银行业全要素生产率测量方法介绍

效率分析是一种静态的比较，为了进行动态分析并得到全要素生产率指数、技术效率指数和技术进步指数，我们对Akther等(2013)的银行效率评价模型进行了拓展，设计了3个跨期效率测量模型(式(5)-式(7))，再依据以上四个效率测量模型，根据Cooper等(2004)对松弛情况下Malmquist指数的计算设定，以及Tone和Tsutsui(2013)对网络结构下Malmquist指数的计算思想，得到本文的Malmquist指数式(8)及其分解式(9)和式(10)。

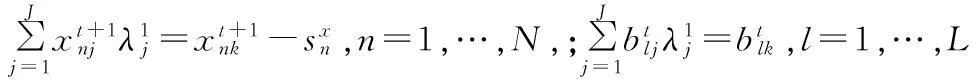
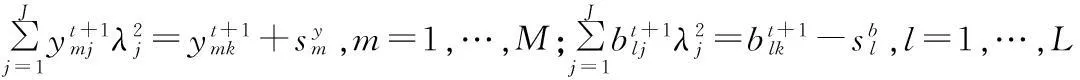
(5)

其中，NSBI2表示以t+1期的技术为参照系时t+1期的非效率值。

(6)

其中，NSBI3表示以t+1期的技术为参照系时t期的非效率值。

(7)

其中，NSBI4表示以t期的技术为参照系时t+1期的效率值。

由于NSBI1、NSBI2、NSBI3和NSBI4表示非效率项的大小，在构造Malmquist指数时，我们采用效率项的大小。为此，我们采用Chung等(1997)的公式，将非效率值加1后取倒数得到效率值的大小，其中SBI1=1/(1+NSBI1)，SBI2=1/(1+NSBI2)，SBI3=1/(1+NSBI3)和SBI4=1/(1+NSBI4)。根据以上四个距离函数，我们可以根据Färe等(1994)以及Tone和Tsutsui(2013)提出的各种分解Malmquist指数的思想，得到全要素生产率指数及其分解式。

(8)

(9)

(10)

(11)

(三)数据来源

上市银行是中国银行业的主体，对这些银行的效率评价可以为其他银行的评价提供借鉴。目前，我国共有16家上市银行，包括4家国有商业银行：中国银行、中国建设银行、中国工商银行和中国农业银行；3家城市商业银行：北京银行、南京银行和宁波银行；9家股份制银行：交通银行、中国民生银行、光大银行、华夏银行、平安银行、兴业银行、浦发银行、招商银行和中信银行。数据包络分析的经验规则认为决策单元数目n应该满足n≥max{m×s,3(m+s)}，其中m为投入指标数，s为产出指标数(Cooper等，2007)。为此，本文选择16家上市银行2004-2012年的数据进行分析，第一阶段有四种投入和两种产出，第二阶段有两种投入和三种产出。但也有文献认为这并不是必须满足的条件(Cook等，2014)，这个问题还在争论之中。

银行效率评价既取决于评价方法的选择，也取决于投入和产出指标的选择，银行业投入产出指标的选取是效率评价的重点问题之一，这个问题会导致评价的结果不同。对于投入产出指标的选取主要有生产法(productionapproach)、中介法(intermediationapproach)、资产法(assetsapproach)、增值法(valueaddedapproach)和用户成本法(user-costapproach)。Berger和Humphrey(1997)认为现实中较为常用的方法是前两种，但是实证研究中会出现多种指标的结合应用。传统的银行业效率评价文献将银行业的生产过程看成“黑箱”，只考虑了投入和产出数据，而没有考虑中间生产过程，且不少文献也没有考虑以不良贷款表示的非期望产出。根据对银行业生产过程的两阶段网络模型的设定，本文投入和产出指标的选择主要从生产法的角度来考虑，这一考虑与国内文献中将生产法和中介法结合考虑相类似。其实对于生产法，在中国的存贷款利率市场化程度不高的情况下，银行业很多费用标准是相同的，只取决于投入和产出。从这个方面看，生产法的效果与中介法、增值法的指标也有类似之处。

每一期的第一阶段投入包括固定资产净值、员工人数、股权资本以及上一期的不良贷款。将上一期的不良贷款看成投入，因为贷款质量的高低与银行效率直接相关，如果不良贷款较多，银行就必须用较多的利润对坏账进行冲销，或提取较多的坏账准备以应对未来可能出现的风险，或增加股权资本，从财务杠杆的角度看也会限制吸收存款的数量，因此本文将它看成投入，这种处理与国内大多数文献是不同的。Akther等(2013)采用的就是这一处理方式，它与巴塞尔协议Ⅲ对风险资本标准的要求是一致的。第一阶段的产出用存款来表示，存款是中间产品，也是第二阶段的投入，这与Seiford和Zhu(1999)的做法是一致的。第二阶段的产出用贷款、不良贷款和投资来表示，本文的投资包括债券投资和股权投资。由于银行业的股权投资限制比较严格，从数据来看很多银行都没有该项投资，债券投资占绝大部分的比重。

根据两阶段网络模型的设定，每期的效率评价需要上一期的非期望产出作为投入。我们采用GDP的缩减因子对上一期的非期望产出数据进行处理，得到当年的不变价指标。为了进行跨期的比较，也需要进行缩减，所以我们对所有数据进行了不变价处理。以上数据来自《中国统计年鉴》、《中国金融年鉴》、Bankscope以及各上市银行年报或财务报告。

四、实证结果分析

根据两阶段网络方向性距离函数模型(式(2))和两阶段网络方向性距离松弛的数据包络模型(式(3))，我们可以得到16家上市银行的非效率项大小，选择式(2)主要为了与式(3)的结果进行比较。在实际计算中，两类模型方向性向量的选择有很多标准。本文采用标准的设定，以自身的数值作为方向性向量对目标函数中的松弛量进行调整，这也是很多文献采用的方法，这样非效率项的评价值在0到1之间。

(一)银行业效率分析结果与模型比较研究

通过两阶段网络方向性距离松弛的数据包络模型(式(3))，我们可以得到非效率测算结果。从表1中可以看到，2005-2012年各家银行多数年份都出现非效率，特别是华夏银行每年的非效率项数值都比较大。例如，2007年华夏银行的非效率项数值为0.5163。根据方向性距离函数中的方向选择，华夏银行2007年的固定资产净值为41.21亿元，从业人员为9 390人，股权资本为5 923.38亿元，贷款为2 985.49亿元，投资为689.74亿元，不良贷款为68.9亿元。如果按照方向性向量调整，只需要固定资产净值41.21×(1-0.5163)亿元，从业人员9 390×(1-0.5163)人，股权资本5 923.38×(1-0.5163)亿元，就能得到贷款2 985.49×(1+0.5163)亿元，投资689.74×(1+0.5163)亿元，不良贷款68.9×(1-0.5163)亿元的结果。2005年处在前沿面即有效率的银行共有3家，分别是中国民生银行、宁波银行和兴业银行。非效率项数值最大的是中国银行，其次是交通银行，以及中国工商银行、中国农业银行、光大银行等。这个评价结果表明，有效率的银行都是地区性银行和股份制银行，排名靠后的都是国有商业银行。例如，2005年中国建设银行的非效率值为0.3253，在成立较早和国有股份制银行中是最小的，但仍排在第11位。2006年延续了2005年的评价结果，不过中国农业银行的业绩最差，排在最后，四大国有股份制银行和交通银行仍排名靠后。2007年处在前沿面的银行只有宁波银行1家，其他银行都出现了无效率的状况，且很多银行离前沿面更远，其中一个显著的变化是华夏银行以非效率数值0.5163排名倒数第一，其他国有商业银行紧随其后。2008年的非效率得分情况与2007年基本相似，不过中国农业银行的排名在国有银行中明显靠前。2009年和2010年华夏银行继续排名靠后，离前沿面的距离较2007年有所好转。2011年和2012年与前面年份相比较的一个显著特点是，处在前沿面的银行增加了1家，非效率项数值较前两年也有所降低，说明这两年银行业的整体效率有所上升。本文的分析结果特别是2007年和2008年的效率比较低与张健华和王鹏(2010)的分析结论是一致的。

从单个银行来看，对于2005-2012年的平均非效率项，16家银行中兴业银行最小，为0.0288，8年中有5年处在前沿面上，其次是宁波银行，为0.0699，8年中有4年处在前沿面上。排名靠后的3家银行依次是华夏银行、中国农业银行和中国银行，两家国有商业银行和一家股份制银行。从时间维度来看，2005-2012年每家银行的非效率项呈现出一种倒U形变化趋势，银行非效率项最近两年逐渐变小，经营业绩有所好转。从所有银行的平均情况来看，非效率项的均值从小到大依次出现在2012年、2011年、2010年、2008年、2009年、2005年、2006年和2007年。这表明非效率项的数值随时间变得越来越小，离前沿面的距离越来越近，银行业的业绩整体上在2010-2012年有大幅提高。从时间维度来看，这些年份银行业的非效率呈现出倒U形变化趋势，这与单个银行的趋势是类似的。出现这种状况的原因在于：一方面，宏观经济形势好转，导致投资收益高和企业贷款违约率低；另一方面，得益于银行自身微观制度的规范，如银行贷款的严格审批和核准程序以及贷款发放和收回责任制等，不良贷款率大大降低，而存款和贷款的利差是稳定的，从而导致近年来银行业效率逐渐提高，即非效率项出现下降趋势。2008年的效率出现下降，主要是因为这一年的投入和产出组合不是非常有效，如不良贷款率下降并不多，但是各家银行的资产规模等变量却变得较大。

表1　16家上市银行2005-2012年的非效率值

表1的分析结果表明，华夏银行的业绩较差，其次是国有商业银行中的中国农业银行和中国银行，这与现实中这几家银行的经营结果是一致的。我们通过收集银行的财务报告信息，发现2007年和2008年，华夏银行的加权风险资产收益率分别为0.8%和1.26%，在当时14家上市银行中排名倒数第一。在资本充足率方面，2007年年报显示其核心资本充足率和资本充足率分别为4.3%和8.27%，已经接近4%和8%的监管红线。在不良贷款率方面，华夏银行2010年为1.18%，仅次于中国农业银行的2.03%；2011年为0.92%，仅低于四大国有商业银行；2012年为0.88%，低于交通银行、平安银行、中国银行、中国建设银行和中国农业银行。在上述的非效率分析中，我们看到中国农业银行的非效率值始终排在前两位。图1显示，中国农业银行的不良贷款率较高，加之其贷款量较大，不良贷款量也是所有银行中最大的。从资本充足率看，2005年中国农业银行的股权资本为-7 276.05亿元，处于资不抵债的状态。光大银行2005-2012年的平均非效率值为0.2899，排名第四，这从光大银行2005年和2006年的所有者权益分别为-1.47亿元和-0.39亿元中有所反映，同样是一种资不抵债的情况。中国银行2005-2012年的平均非效率值为0.3021，在16家银行中排在第三位，这与其不良贷款率一直处于较高水平有一定的关系。

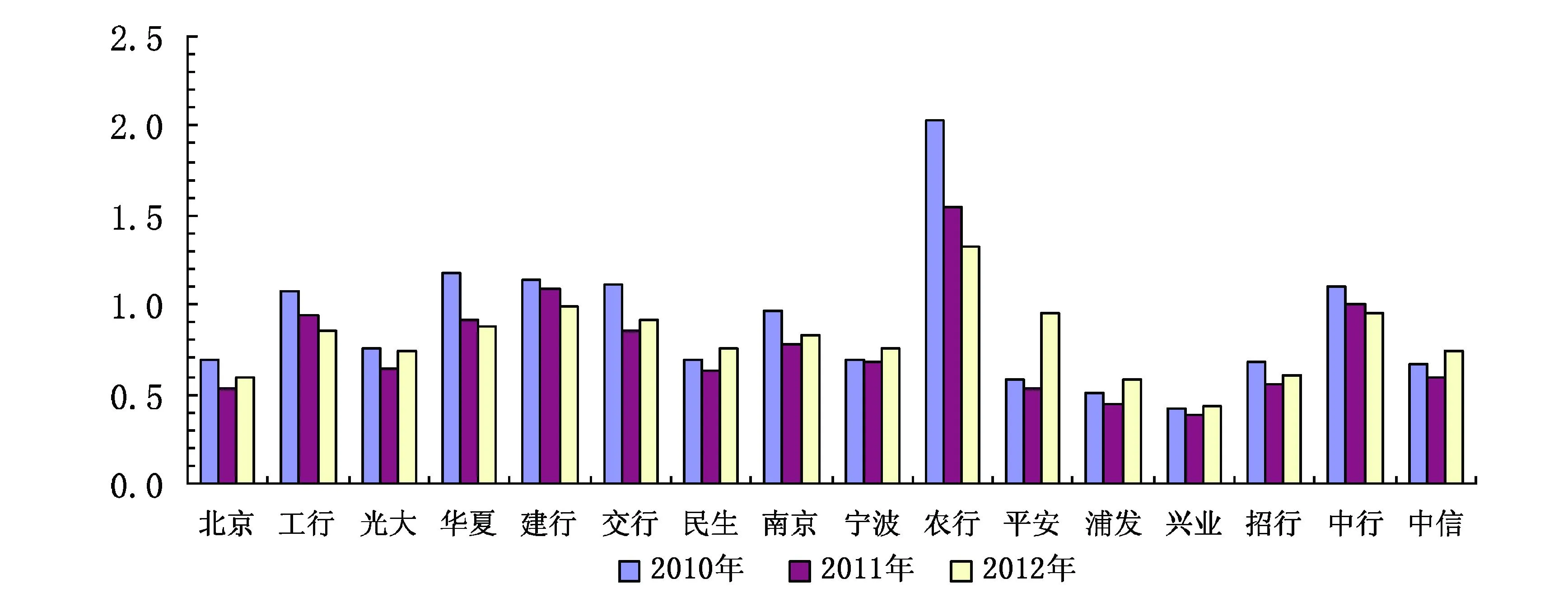
图1　16家上市银行2010-2012年的不良贷款率(单位：%)

表1的结果相对较为合理，与银行业的实际表现也是基本吻合的。为了比较其他模型的效果，我们采用式(2)即没有考虑松弛情况下的非效率项度量方法，选择与表1相同的方向性向量，估计结果见表2。我们发现这种评价结果与表1的结果存在非常大的区别。其中显著的特点是各年中国农业银行都处在前沿面上，是经营业绩最好的银行，其次是北京银行。其他4家国有股份制银行的非效率项数值也较大，这与中国农业银行的极端取值有一定的关系，这种方法的分辨能力不是非常强。另外，每年处在前沿面上的银行数目都较多，分辨能力较差，但2007年和2008年华夏银行也是表现最差的银行。从2005-2012年每家银行的均值来看，除了中国农业银行没有非效率情况外，其他银行都出现了非效率。从时间维度来看，2005年的平均非效率值为0.0282，2008年为0.0546，随后出现下降的趋势，2012年的平均非效率值为0.0215，可见这些年份的效率变化呈现出倒U形趋势。这种分析方法显然没有由式(3)分析得到的结果好，而且两种估计方法的差距比较大。在下文影响效率的因素分析中，我们主要采用了表1中的非效率数据。

表2　没有考虑松弛情况下的非效率估计结果

(二)银行全要素生产率分析

非效率反映了离前沿面的距离，是一种静态的相对比较。为了反映全要素生产率的变化，我们采用这些距离函数，根据Färe等(1994)以及Tone和Tsutsui(2013)构造Malmquist指数的思想得到网络情况下的全要素生产率指数及其分解后的技术进步指数和技术效率指数。根据式(8)，全要素生产率指数见表3。从中可以看到，全要素生产率下降的三家银行分别是华夏银行、中国民生银行和中国农业银行。这与效率分析结果是基本对应的，特别是华夏银行和中国农业银行的效率本身也较低，中国民生银行的全要素生产率出现下降，主要是因为2009年、2010年和2012年这3年的非效率项数值较大，导致全要素生产率下降。其他13家银行的全要素生产率都出现了上升，特别是浦发银行、兴业银行、平安银行、招商银行和中信银行的全要素生产率增长都在20%以上。另外，每家银行或者全部银行的平均全要素生产率指数都出现了上升的趋势，表明银行业的整体经营绩效有了大幅的改善。我们对全要素生产率指数进行分解得到了技术效率指数，*为了节省篇幅，文中未给出技术效率指数和技术进步指数的分解结果，如有需要可向作者索要。发现华夏银行和中国民生银行的排名没有改变。由于技术效率反映的主要是管理经验，这两家银行的全要素生产率较低与其管理水平较低有一定的关系，而且这两家银行与前沿银行管理水平的差距呈现拉大的趋势。这一分析结果表明股份制银行的管理不一定就比国有银行要好，大的国有商业银行在历史积淀、研发投入和人才方面有一定的优势。

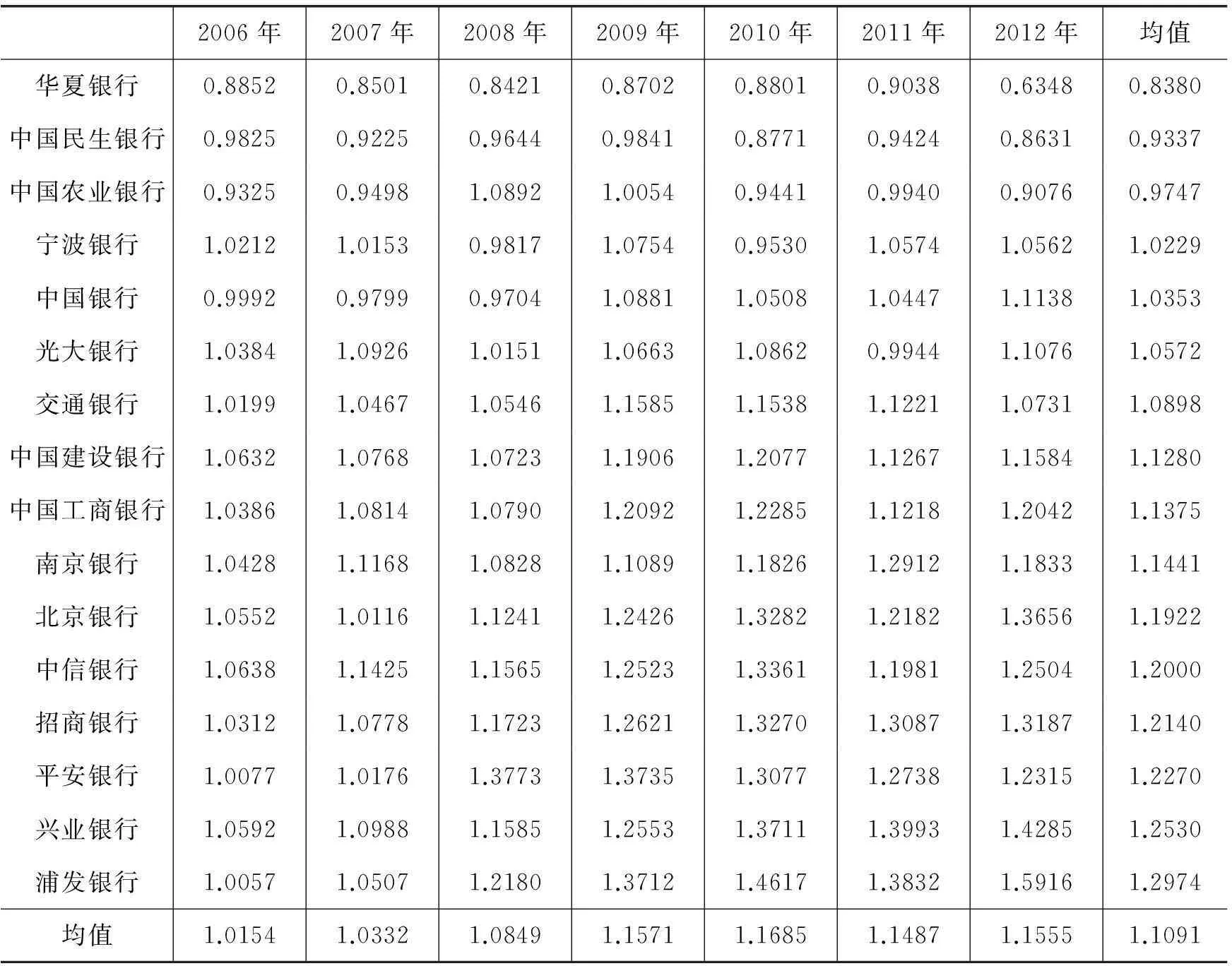
表3　2006-2012年16家上市银行的全要素生产率指数

从技术进步指数来看，四大国有银行的技术进步指数的排名都靠后，这与王兵和朱宁(2011)的结论是一致的。他们的解释是“低悬的果实”摘取殆尽，即技术进步已经到了一定的水平，技术复杂性增加得较快，要想在原有技术上取得突破非常困难。而股份制和地区性银行的技术水平较低，在技术模仿和技术引进方面有着很大的空间，导致技术进步指数上升较大。这与现实中国有银行的研发资金与人员投入较大是相对应的。我国四大国有银行成立较早，资产规模较大，而且都有自己的研发部；而很多地区性银行和股份制银行没有相应的研发部，为了节省研发费用，很多设备和技术都是从国有银行和国外购置得到的。从实证结果可以看到，全要素生产率的上升是技术进步和技术效率提高共同作用的结果，很难区分其中是技术进步的贡献大还是技术效率提高的贡献大。

五、银行业非效率的影响因素分析

造成银行间效率差距的因素有哪些？这是很多研究银行效率文献和决策者关心的问题之一，但是相关研究并没有得到一致的结论。Berger和Humphrey(1997)认为这主要取决于效率的度量方法、效率的概念和变量的选取。张健华(2003)及张健华和王鹏(2010)从银行业的内部和外部选取了影响其效率的因素。王兵和朱宁(2011)主要选取外部宏观环境因素对银行业的全要素生产率进行了实证分析。Assaf等(2013)则选择了各家银行存款的市场份额(MSD)、分支机构(BRANCH)、资产回报率(ROA)、净利息收益率(NetInterestMargin，NIM)以及前五大行的存款比重。Fukuyama和Weber(2009)选择了银行存款的市场份额、净利息收益率、资本充足率(CAPEQ)、成立时间(Age)和银行资产的自然对数这5个变量对非效率项进行了研究。Fukuyama和Matousek(2011)选择的变量更多，包括净利息收益率、非利息收入率、资产回报率、存款市场份额、贷款市场份额、产权结构虚拟变量、成立时间和资本充足率等。

参考已有研究，本文选择了9个银行业内部变量和1个宏观经济变量即GDP增长速度对银行业非效率的影响因素进行分析。银行业内部变量主要有：(1)净利息收益率(NIM)：用净利息收入除以生息资产来表示，用于衡量银行的存贷盈利能力和管理质量。(2)分支机构数量(BRANCH)：该指标既反映了服务的可及性和质量，也反映了银行经营成本的上升。(3)市场势力：用存款或贷款份额(MSL)或资产比重(ZC)来表示，这几个变量存在共线性，在回归分析中采用其中一个变量，其他两个变量用于检验稳健性。(4)资产回报率(ROA)：用净收入占总资产的比例来表示，反映银行的经营表现。(5)产权结构(Dummy)：国有银行取1，股份制银行取0。张健华(2003)以及Fukuyama和Matousek(2011)发现产权结构对效率的影响不显著，没有证据表明国有银行的效率比股份制银行要低，这一结论不支持“平静生活理论(quietlifetheory)”。*Berger和Hannan(1998)利用美国20世纪80年代5 000家银行的数据，发现银行业高的市场集中度即低的竞争度与成本低效率联系在一起，因为大型银行利用其垄断地位发挥定价的优势，对成本的降低并不是很关心，所以以损失效率换取利润最大化，享受“平静生活”。(6)资本充足率(CAPEQ)：该指标常被用来衡量银行经营的风险性，是影响银行效率的主要因素，巴塞尔协议对该指标一直有着严格的规定，特别是2010年末的巴塞尔协议Ⅲ对资本充足率更是非常重视；此外，资本充足率也是实际经营成本的重要影响因素之一。(7)贷款与存款之比(Deposit)：该指标反映银行的资产配置情况，体现资产配置效率，该指标数值越高通常表明银行的效率越高。(8)中间业务收入(Inter)：该指标反映银行的效率高低，我们对该指标取对数。(9)银行成立时间的对数(Age)：该指标反映学习效应的大小。上述数据与第三部分效率评价中的数据来源是一致的。

由于银行业技术非效率的取值大于等于0，是一种明显的左截断分布，用经典回归分析方法建立模型有可能会得到负的拟合值。Maudos和 de Guevara(2007)采用Logit回归模型来分析影响因素的作用，但是更多的文献采用受限因变量的面板Tobit模型来研究技术效率的影响因素。对受限因变量面板数据模型而言，固定效应Tobit模型通常不能得到一致的估计值，因此本文采用随机效应Tobit模型。我们选择第三部分得到的NSBI1作为因变量，上述的银行内部因素和宏观环境因素共10个变量作为解释变量，建立了以下的面板随机效应Tobit模型：

+β6Depositit+β7Interit+β8Ageit+β9Dummyi+β10GDPt+εit

(12)

表4报告了随机效应面板Tobit模型的回归结果，随机效应非常显著，表明采用的模型是合适的。其中，列(1)是对所有10个变量进行回归的结果；列(2)是剔除了列(1)中不显著的经济发展水平变量后的回归结果，所有变量系数的符号与列(1)相同，但是资本充足率仍不显著；列(3)中剔除了经济发展水平和资本充足率两个变量，所有变量在20%的显著性水平上是可以接受的，且系数符号与列(1)中相同，所以下文主要依据列(1)的结果进行分析。

表4　银行业非效率项的影响因素分析

从表4中可以看到，净利息收益率的系数显著为正，表明净利息收益率增加导致非效率项数值增加。这与Fukuyama和Weber(2009)的结论是一致的，他们认为这个结果表明银行业有着较高的边际收益，会使经理们从事成本较高的项目投资，从而抵消了效率的增长。我们用存款比重来表示市场份额，结果表明其增加降低了非效率项数值，而且在5%的水平上显著，Maudos和de Guevara(2007)的解释是：市场势力的存在会导致银行的投入成本降低，由于规模报酬递增，规模大的银行平均成本较低，本文的结果支持了他们的分析。为了保证稳健性，我们用贷款份额或资产比重重新进行回归，结果并没有改变。Benston(1972)的研究也表明，在其他投入和产出要素不变的情况下，银行规模扩大1倍，平均成本下降5%-8%。贷款与存款之比的结果并不显著，按照效率银行的要求，其系数为负，该项指标值越高表明银行的非效率值越小，即有效率的银行贷存比结构较好。本文的结果不支持这个假设。资本充足率的系数按照理论预期也应为负，即资本充足率高的银行效率应更高，但是本文的结果并不支持这一理论预期。资本充足率的高低反映了银行的经营风险，但是对于我国银行业资本充足率的要求，主要是为满足国际规则和市场化改革的需要而设置的，而其经营风险通常是以国家信用为担保，不存在破产风险，从而导致该项指标没有西方国家对效率的影响明显。资产回报率的系数显著为负，这与多数研究的结论是一致的，收益率高的银行经营业绩更好，有限的资金创造了最大的收益。中间业务收入可以看成是效率的表现，也可以理解为金融创新。本文中中间业务收入的系数为负，表明该指标提高导致非效率下降，这与多数研究的结论是类似的，但是其系数并不显著。对于分支机构的作用，Fukuyama和Matousek(2011)认为分支机构较多会导致成本上升，从而非效率项数值上升，本文中其系数显著为正，这与他们的结论是一致的。分支机构多会耗费大量的成本，国有银行的分支机构较多且遍布城乡，而股份制银行则主要分布在经济发达的城市部门。从这个方面看，股份制银行对分支机构的设置也是有效的。宏观经济变量GDP增长速度对效率的影响并不明显，银行业效率主要受到自身内部因素的影响。产权结构的影响不显著，支持了“平静生活理论(quietlifetheory)”，即国有产权和市场份额较大的银行在市场竞争中的效率较低，这与针对国外银行业的研究结论是一致的，张健华(2003)的研究也支持了这个结果。银行的成立时间反映了其学习效应，但是本文的结果与这个观点相反，主要是因为成立较早的国有商业银行的政策性负担较大，其次是不良贷款较多、机构和退休人员数量较大等，从而抵消了学习效应所导致的效率上升。

六、结论与启示

本文运用中国16家上市银行2004-2012年的数据，将银行业的生产看成一个两阶段网络生产过程，并考虑了银行业的不良贷款作为非期望产出时的弱可处置性问题，运用两阶段网络方向性距离松弛的数据包络模型对我国银行业的效率与全要素生产率进行了较系统的实证研究，得到以下结论：

(1)银行业的效率评价与不良贷款的比率有着密切的关系，以往不考虑不良贷款的非参数估计方法所得结果有可能不稳健。首先，根据本文的评价方法，华夏银行的效率最低，这与其不良贷款比率偏高显著相关；其次，国有银行的效率仍然偏低，四大国有银行排在后七位。我国国有银行的不良贷款比率排在前5位，其中中国农业银行的不良贷款率明显高于华夏银行。

(2)两阶段网络方向性距离松弛的数据包络模型分析表明，每年处在前沿面的银行非常少，各家银行都存在非效率现象；从单个银行和所有银行平均的时间维度看，效率变化呈现出倒U形的趋势，但是近几年银行业效率显著提高。

(3)银行业效率评价方法的选择对评价结果是否科学非常关键，没有考虑松弛作用时对效率的估计结果与考虑时的结果差别很大。比如，没有考虑松弛作用时对中国农业银行的效率评价结果明显不符合事实；同时，每年处在前沿面的银行数目也较多，非效率数值明显偏小，最大也不超过7%，这与我们通常的理解显然不相吻合。

(4)全要素生产率的分析结果表明，银行业的业绩整体变好。银行业全要素生产率的增长是技术进步和技术效率提高共同作用的结果，其中三家银行的全要素生产率指数下降主要是近几年非效率上升所导致的，其他银行则在技术进步和技术效率提高的共同作用下出现了上升的趋势。

(5)影响银行业效率的因素主要来自银行业内部。本文选取了9个银行业内部变量和1个宏观经济变量，发现宏观经济变量对银行业效率的影响并不显著。另外，影响银行业效率的变量在发达国家显著，而在中国有可能不显著，但是多数影响银行业效率的变量与国内外研究的结论基本一致。

根据本文的分析结果，近年来我国银行业的效率和全要素生产率有大幅上升的趋势。这主要得益于2003年以来推行的国有银行股份制改造和公开上市所产生的正向效应，这些措施在某种程度上硬化了国有银行的预算约束。但国有商业银行的效率仍偏低，股份制银行的政策性负担则相对较少，导致整体效率较高。这提醒我们对于国有银行，要优化银行的内部治理结构和去行政化，硬化其预算约束，真正解决委托代理问题和道德风险问题，提高效率。

--------------

主要参考文献：

[1]蔡跃洲，郭梅军.我国上市商业银行全要素生产率的实证分析[J].经济研究，2009，(9)：52-65.

[2]柯孔林，冯宗宪.中国银行业全要素生产率测度：基于Malmquist-Luenberger指数研究[J].数量经济技术经济研究，2008，(4)：110-120.

[3]王兵，朱宁.不良贷款约束下的中国上市商业银行效率和全要素生产率研究——基于SBM方向性距离函数的实证分析[J].金融研究，2011，(1)：110-130.

[4]薛峰，杨德礼.评价银行经营与管理综合效益的DEA模型[J].数量经济技术经济研究，1998，(5)：63-66.

[5]张健华.我国商业银行效率研究的DEA方法及1997-2001年效率的实证分析[J].金融研究，2003，(3)：11-25.

[6]张健华，王鹏.中国银行业广义Malmquist生产率指数研究[J].经济研究，2010，(8)：128-140.

[7]Akther S, Fukuyama H, Weber W L. Estimating two-stage network slacks-based inefficiency: An application to Bangladesh banking[J]. Omega, 2013, 41(1): 88-96.

[8]Assaf A G,Matousek R, Tsionas E G. Turkish bank efficiency: Bayesian estimation with undesirable outputs[J]. Journal of Banking and Finance, 2013, 37(2): 506-517.

[9]Benston G J. Economies of scale of financial institutions[J]. Journal of Money, Credit and Banking, 1972, 4(2): 312-341.

[10]Berg S A,Førsund F R,Hjalmarsson L, et al. Banking efficiency in the Nordic countries[J]. Journal of Banking and Finance, 1993, 17(2): 371-388.

[11]Berger A N, Humphrey D B. Efficiency of financial institutions: International survey and directions for future research[J]. European Journal of Operation Research, 1997, 98(2): 175-212.

[12]Chambers R G, Chung Y, Färe R. Benefit and distance functions[J]. Journal of Economics Theory, 1996, 70(2): 407-419.

[13]Charnes A,Cooper W W,Golany B，et al. Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions[J]. Journal of Econometrics, 1985, 30(1): 91-107.

[14]Chen Y, Cook W D, Li N, et al. Aditive efficiency decomposition in two-stage DEA[J]. European Journal of Operational Research, 2009, 196(3): 1170-1176.

[15]Chung Y, Färe R, Grosskopf S. Productivity and undesirable outputs: A directional distance function approach[J]. Journal of Environmental Management, 1997, 51(3): 229-240.

[16]Cook W D, Tone K, Zhu J. Data envelopment analysis: Prior to choosing a model[J]. Omega, 2014, 44(1): 1-4.

[17]Cooper W W, Seiford L M, Tone K. Data envelopment analysis: A comprehensive text with models, applications, references and DEA-solver software[M].Berlin：Springer, 2007.

[18]Cooper W W, Seiford L M, Zhu J. Handbook on data envelopment analysis[M].Berlin:Springer, 2011.

[19]Färe R, Grosskopf S, Lovell C. The measurement of efficiency of production[M]. Boston:Kluwer-Nijhoff, 1985.

[20]Färe R, Grosskopf S, Norris M, et al. Productivity growth, technical progress, and efficiency change in industrialized countries[J]. American Economic Review,1994,84(1):66-83.

[21]Färe R, Grosskopf S, Pasurka C. Environmental production functions and environmental directional distance functions[J]. Energy, 2007, 32(7): 1055-1066.

[22]Fethi M D, Pasiouras F. Assessing bank efficiency and performance with operational research and artificial intelligence techniques: A survey[J]. European Journal of Operational Research, 2010, 204(2):189-198.

[23]Fujii H, Managi S, Matousek R. Indian bank efficiency and productivity changes with undesirable outputs: A disaggregated approach[J]. Journal of Banking and Finance, 2014, 38: 41-50.

[24]Fukuyama H, Matousek R. Efficiency of Turkish banking: Two-stage network system[J]. Journal of International Financial Markets, Institutions and Money, 2011, 21(1): 75-91.

[25]Fukuyama H, Weber W L. A directional slacks-based measure of technical inefficiency[J]. Socio-Economic Planning Sciences, 2009, 43(4): 274-287.

[26]Holod D, Lewis H F. Resolving the deposit dilemma: A new DEA bank efficiency model[J]. Journal of Banking and Finance, 2011, 35(11): 2801-2810.

[27]Isik I, Hassan M K. Technical, scale and allocative efficiencies of Turkish banking industry[J]. Journal of Banking and Finance, 2002, 26(4): 719-766.

[28]Kao C, Hwang S N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan[J]. European Journal of Operational Research, 2008, 185(1): 418-429.

[29]Liang L, Cook W D, Zhu J. DEA models for two-stage processes: Game approach and efficiency decomposition[J]. Naval Research Logistics, 2008, 55(7): 643-653.

[30]Maudos J, de Guevara J F. The cost of market power in banking: Social welfare loss vs. cost inefficiency[J]. Journal of Banking and Finance, 2007, 31(7): 2103-2125.

[31]Seiford L M, Zhu J. Profitability and marketability of the top 55 US commercial banks[J]. Management Science, 1999, 45(9): 1270-1288.

[32]Sherman D, Gold F. Branch operating efficiency: Evaluation with data envelopment analysis[J]. Journal of Banking and Finance, 1985, 9(2): 297-315.

[33]Tone K. A slacks based measure of efficiency in data envelopment analysis[J]. European Journal of Operational Research, 2001, 130(3): 498-509.

[34]Tone K, Tsutsui M. Dynamic DEA with network structure: A slacks-based measure approach[R]. Workshop on DNDEA, 2013.

(责任编辑康健)

中图分类号：F830.3

文献标识码：A

文章编号：1001-9952(2015)09-0079-17

收稿日期：2015-02-22

基金项目：国家社科基金项目“资源环境约束下全要素生产率增长的测度方法拓展与实证分析研究”(14BTJ011)；教育部新世纪优秀人才支持计划(NCET-13-0641)；国家社科基金重大项目“大数据与统计学理论的发展研究”(13&ZD148)

作者简介：李小胜(1976-)，男，安徽枞阳人，安徽财经大学统计与应用数学学院副教授；

The Efficiency of Chinese Listed Banks and Total Factor
Productivity：Empirical Analysis Based on Two-stage
Network Directional Distance SBM Model

Li Xiaosheng, Zhang Huanming

(SchoolofStatisticsandAppliedMathematics,AnhuiUniversityof

FinanceandEconomics,Bengbu233030,China)

Abstract：Although many scholars have done a lot of empirical studies on measuring the efficiency of banking industry with data envelopment analysis model, most of the literature does not take the network structure of banking efficiency evaluation into account, and also less considers the undesirable outputs of banking, leading to the challenges of the estimation results. Based on the data of 16 listed banks in China from 2004 to 2012, this paper regards the banking production as a two-stage network production process, and considers the “non-performing loans” as a weak disposability of undesirable outputs. Then it employs a data envelopment model of two-stage directional distance network slacks to make a systematic measurement. It reaches the empirical results as follows: firstly, the efficiency of state-owned banking sector is still relatively low;secondly, there exists the inefficient phenomenon in each bank, but changes in banking efficiency show an inverted U-shape trend; in recent years, the efficiency of the banking sector has improved significantly; thirdly, method choices of efficiency evaluation of the banking sector is very critical to empirical results, and the estimation results without considering the slack effect are different from ones taking the slack effect into account. Total factor productivity (TFP) results show that the overall performance of the banking sector became better, the result of the combination of technological progress and technical efficiency improvement, mainly owing to the hard constraint resulting from the shareholding reform of state-owned banks and the public offering since 2003. It further analyzes the factors affecting the non-efficiency of the banking sector and indicates that macroeconomic factors have no significant effects on the efficiency of the banking sector while the internal factors of the banking have significant effects on the non-efficiency terms.

Key words:two-stage network DEA;directional distance;the efficiency of listed banks