核电站双钢板混凝土剪力墙抗剪强度研究

熊峰 何涛 周宁

摘要：以核电站屏蔽厂房剪力墙为原型，对含栓钉和加劲肋的双钢板混凝土组合剪力墙进行低周往复加载抗剪试验研究.试件包含3个1︰4缩尺模型，变化参数为栓钉间距与加劲肋，分析了试件的破坏特征、承载力以及耗能情况.试验研究发现：组合墙体整体受力性能良好，具有较强的抗剪性能.通过设置加劲肋，能有效提高墙体承载能力、刚度和延性.在试验基础上进行了有限元数值模拟与参数研究，研究了混凝土强度、钢板厚度、轴压力和加劲肋设置对抗剪强度的影响程度，并初步建立了核电站双钢板剪力墙抗剪强度计算公式，为核电安全壳设计理论的建立打下了基础.

关键词：双钢板混凝土剪力墙；栓钉间距；拟静力试验；有限元分析；抗剪强度

中图分类号：TU398.9文献标识码：A

核能作为经济、清洁的能源，在我国有着广阔的发展空间.屏蔽厂房作为核电站的最后一道安全保障，在防止核泄漏、飞机撞击、地震等灾害时有着非常重要的作用.双钢板混凝土组合剪力墙以其良好的防撞击性能、耗能能力以及方便模块化施工的优点在核电站屏蔽厂房中得到了应用.目前我国部分在建和拟建的核电站采用了双层钢板内填混凝土的组合剪力墙体作为屏蔽厂房安全壳[1].

双钢板混凝土组合剪力墙近年来在高层建筑中的应用也很广泛，国内外专家学者对此做了相关的试验研究.Wright等[2-3]对双面压型钢板混凝土剪力墙的受力性能进行了低周往复加载试验，并和数值模拟结果进行了对比，提出了相应的设计方法.罗永峰[4]等在试验基础上建立了双钢板的多组有限元模型，分析了影响墙体承载力的因素.聂建国等[5-6]对双钢板内填高强混凝土的剪力墙试件进行了试验，研究表明，该墙体具有良好的耗能能力和变形能力，适用于超高层建筑，并建立了相应的双钢板剪力墙压弯承载力的简化公式.但大多数双钢板剪力墙的研究都是针对民用建筑，其构造与核电站双钢板剪力墙有明显的差别，例如高层双钢板剪力墙一般设有边缘构件，因此具有较强的抗剪能力.而核电站双钢板剪力墙不仅没有边缘构件，而且通常钢板内也不配受力钢筋.目前针对核电站双钢板剪力墙的研究很少，特别是抗剪性能试验非常缺乏，至今没有抗剪强度计算公式，给核电安全壳设计带来了障碍[7].

本文以AP1000核电站安全壳的双钢板混凝土结构为原型，完成了3个双钢板混凝土剪力墙试件的低周往复加载试验，研究了栓钉间距和设置加劲肋对双钢板混凝土剪力墙抗剪强度的影响.得到墙体的破坏特征、滞回曲线和骨架曲线，分析了墙体的延性、耗能能力、刚度等，并结合有限元数值模拟初步提出了核电站双钢板剪力墙抗剪承载力的简化计算公式.

1试验概况

1.1试件设计

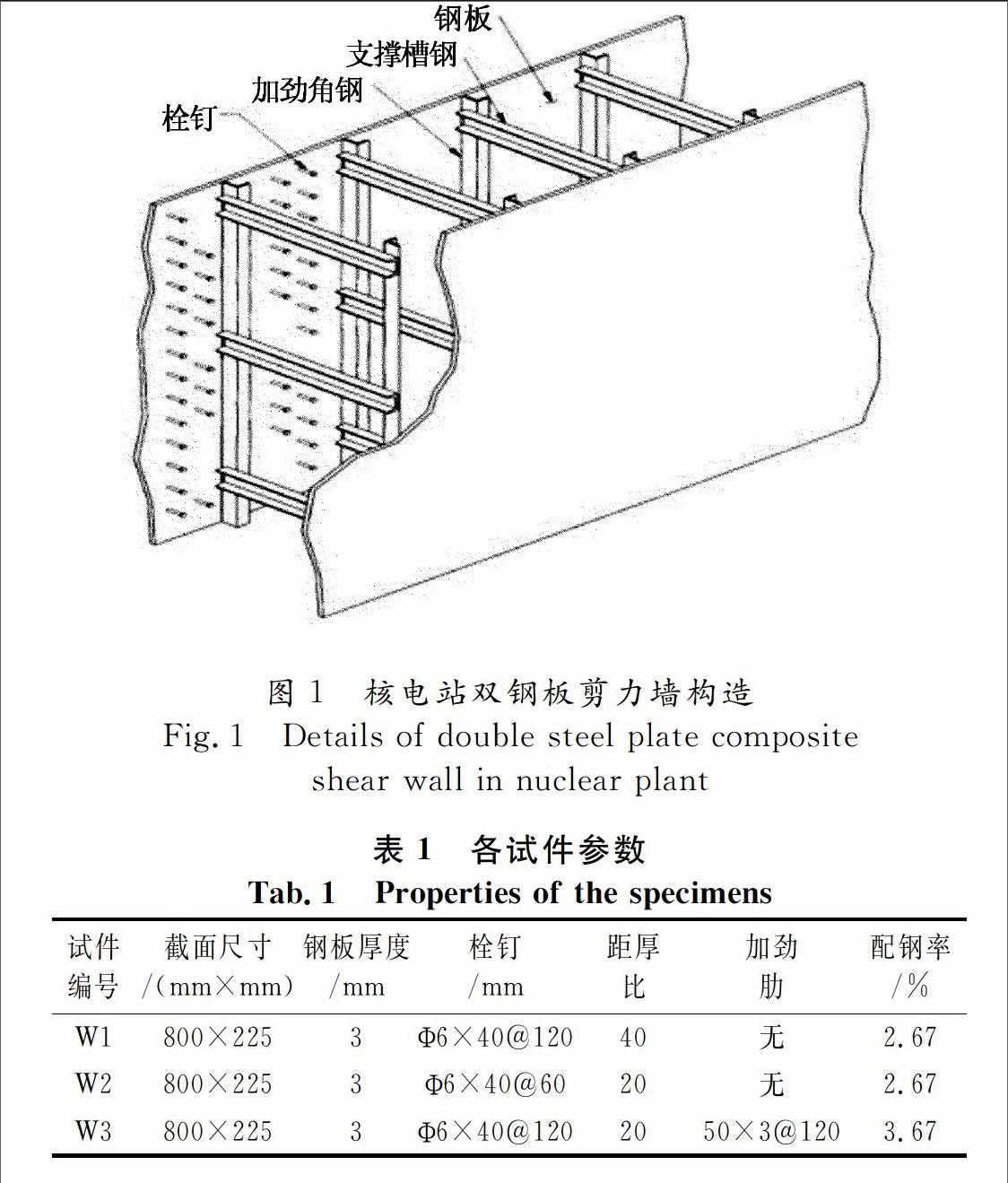
本次试验为核电站双钢板混凝土剪力墙（如图1所示）构件受剪性能的初步试验，主要研究此种构件在与核电站相应的轴压力作用下的剪切破坏特性.后期试验将更详细地研究其在核安全壳中的性能.本文将先对安全壳进行受力分析，在此基础上设计试验试件以模拟在结构中的受力性能.试件取安全壳底部局部部位，采用1/4缩尺模型，墙体高1 600 mm，墙体厚225 mm，钢板厚3 mm.钢板采用Q235，混凝土为C60，栓钉为HPB235.模型墙锚固于350 mm×500 mm的基础梁中，基础梁箍筋采用Φ8mm，纵筋采用Φ18mm.

为考察栓钉间距与竖向加劲肋对墙体抗剪强度的影响，3个试件设置了不同的栓钉间距和加劲肋，均设置间距为240 mm的支撑槽钢，加劲肋采用50 mm×3 mm钢条垂直钢板焊接，栓钉和加劲肋的间距与钢板厚度的比值为距厚比.其参数见表1，试验构件构造如图2所示.

1.2材性试验

墙体混凝土设计强度等级为C60，试件浇筑时，同条件制作养护了3组9个标准立方体试块，测得的混凝土立方抗压强度fcu平均值分别为61.0 MPa， 63.7 MPa和66.3 MPa.钢板、栓钉依照《金属材料室温拉伸试验方法》（GB/T 228—2002）测得其屈服强度fy分别为255 MPa， 495 MPa；抗拉强度fu分别为395 MPa， 595 MPa.

1.3试验装置及加载制度

本次试验采用竖向荷载恒定、水平往复加载的方式.基础梁通过地锚螺栓锚固于试验台，两侧钢板锚入地基梁，并用对拉钢筋连接，与地基梁一同浇

筑.加载梁和墙通过加载梁下翼缘和墙顶预埋板螺栓连接，用以连接水平作动器，施加水平荷载；竖向荷载由竖向作动器施加在位于加载梁上面的分配梁上，并在分配梁与加载梁之间放置滚轴，以保证墙体在水平往复中正常移动.试验加载装置如图3所示.竖向荷载根据墙体在结构中的实际受力取为150 kN.水平荷载的施加采用荷载和位移共同控制，试件屈服前由荷载控制，每次加载取试件预计极限荷载的1/5～1/10，加载初期取20 kN循环一次，逐级增加，后期取40 kN循环一次，直至试件屈服.试件屈服后由位移控制，施加位移取试件屈服位移Δy的倍数，每级取1～3倍屈服位移，逐级加载，直至墙体完全破坏或承载力降到0.85倍极限荷载时试验结束.

1.4测点布置及量测方案

试验量测内容有竖向荷载以及水平往复荷载，试件的水平位移，钢板和混凝土的应变等.位移采用试件顶部和底部放置的激光位移计进行测量，钢板应变片在墙体两侧表面对称布置，每侧钢板布置10个测点，如图4所示.混凝土应变采用内埋式电阻应变计，测点位置与钢板测点对应.

2试验过程及现象

本次试验中各试件的破坏过程基本相似，试件W1和W2均在第13次水平循环加载时宣告破坏，其极限荷载分别为260 kN和250 kN.试件W3最终破坏时的水平循环加载次数为15次，极限荷载为360 kN.试件的最终破坏特征如图5所示.破坏模式均为墙底部与基础梁交界处混凝土开裂引起，由于钢板在混凝土表面，未见有斜裂缝产生.破坏时底部钢板局部有鼓屈，但未拔出.

试件破坏经历4个阶段：弹性阶段，墙体基本保持完好，力位移曲线大致呈线性变化，基本无残余变形；开裂阶段，当各试件荷载达到80 kN， 80 kN和120 kN（各占相应峰值的31%， 30%和33%）时，墙体在与基础梁交界处首先出现细小的水平裂缝，随着水平荷载逐级加大，裂缝逐渐变宽并贯通，可以看出栓钉间距对改善混凝土开裂效果并不明显，而设置加劲肋能较明显地提高试件底部的开裂荷载；屈服阶段，此阶段由荷载位移曲线从明显转折点一直持续到峰值点，裂缝展开明显，试件W1，W2与W3分别在220 kN，240 kN与285 kN的荷载下在脚部发生钢板局部屈曲；破坏阶段，当墙体达到极限荷载时，墙体变形急剧增大，裂缝发展变快，随着荷载往复循环，墙和基梁交界处裂缝宽度和深度继续增大，基础梁混凝土局部挤碎，基础中受拉侧钢板出现滑移并伴随“啪啪”的响声，各试件水平荷载低于峰值的85%，试件破坏.可以看出，墙体破坏是由墙体底部与基础梁交界部位引起，说明此处锚固不足，可能降低了墙体的承载力.设置加劲肋对墙体各方面性能提升明显，承载力提高了近50%.

3试验结果及分析

3.1滞回曲线和骨架曲线

各试件的顶点水平荷载滞回曲线如图6所示.

可以看出在弹性阶段，滞回曲线近似为一条直线，斜率较大，基本没有残余变形.在开裂阶段，滞回环面积逐渐增大，试件开始耗能，滞回曲线的斜率逐渐减小，出现一定的残余变形.屈服阶段，滞回曲线呈S形发展趋势，在原点附近出现捏拢，滞回环面积继续增大，试件耗能增强，残余变形较大.极限阶段，滞回曲线呈反S形发展趋势，此时滞回环面积最大，试件呈现出一定的滑移，滞回曲线斜率继续降低.破坏阶段，滞回曲线呈Z形发展趋势，试件出现大量的滑移，承载能力逐渐减小，呈现出良好的延性和耗能能力.从图6得出在同一荷载作用下，试件W3的滞回曲线斜率和滞回环面积最大，表明墙体设置加劲肋后刚度增大，墙体耗能能力增强.试件W2的曲线斜率较W1大，极限变形也较大，表明减小栓钉间距对墙体刚度和耗能能力有所加强.

各试件的顶点水平荷载位移骨架曲线如图7所示，在弹性阶段，3个试件骨架曲线斜率相近，而弹塑性阶段试件W3较试件W1和W2大，且试件W3弹塑性阶段更长，表明设置加劲肋能有效提高墙体的承载能力、刚度和延性.在弹塑性阶段试件W2的骨架曲线斜率大于W1，且在破坏阶段骨架曲线较W1平缓，表明试件W2延性比W1好.

3.2承载能力与耗能

各试件的特征荷载、对应的水平位移、耗能能力以及延性系数见表2.各试件刚度退化曲线如图8所示.其中，开裂荷载取试件第一条裂缝出现时对应的荷载值，极限荷载取试件在加载过程中的最大荷载值，屈服荷载取底部钢板应变达到屈服应变时的荷载值.破坏荷载取试件破坏时或承载能力低于0.85倍极限荷载时对应的荷载值.本文采用文献[7]中所取方法来确定延性系数μ，以评估试件延性性能.采用功比指数[8]来评价试件耗能能力.

分析表2以及图8可知：

1）承载力对比表明：试件W1和W2的极限荷载与破坏荷载相近，栓钉间距对构件承载能力基本无影响，但是栓钉间距减小能增强钢板和混凝土的连接，防止钢板局部屈曲.试件W3的极限荷载和破坏荷载均较试件W1和W2提高了50%，表明试件W3中设置加劲肋并将其延伸到基础的构造增强了墙体和基础的连接，提高了墙体的承载能力和耗能能力.

2）延性系数：各试件延性系数均大于4，表明双钢板混凝土剪力墙具有良好的延性性能.试件W2较W1提高38%，W3较W1提高66%，表明减小栓钉间距对墙体延性有一定增强，而设置加劲肋对提高墙体延性则有重要作用.

3）耗能能力：试件W1和W2的功比指数相同，表明栓钉间距对墙体耗能能力影响很小；试件W3的功比指数比试件W1和W2均高87.9%，表明设置加劲肋有利于提高墙体的耗能能力，增强墙体的抗震性能.

4）试件刚度退化曲线表明：除去试件初期加载出现的刚度略微跳跃现象，各试件刚度下降大致分为3段，快速下降段、次降速段和缓慢降速段，降幅分别约为62%，20%和8%.试件W3各个阶段的刚度明显大于试件W1和W2，裂缝发展初期刚度退化速度略小于W1和W2，后期稍有增大，表明设置加劲肋后，墙体刚度明显增大.试件W1和W2刚度大小及退化速率接近，表明栓钉间距对墙体刚度影响不大.

3片钢板混凝土剪力墙的低周水平往复加载试验显示：双钢板混凝土剪力墙具有良好的承载力、延性、耗能能力和刚度，两侧钢板和混凝土相互约束，使得墙体受力性能良好，整体性较强.栓钉间距影响钢板和混凝土之间的连接，减小栓钉间距能较好地防止钢板面外局部屈曲，但对承载力提高有限.通过设置加劲肋的构造措施，能有效提高墙体的承载能力、刚度和延性，增大墙体的耗能能力，对墙体抗震性能有重要影响.墙体底部是墙体的主要破坏部位，应加强墙体底部的连接构造.

4双钢板混凝土剪力墙非线性有限元分析

4.1ABAQUS模型建立

为进一步研究双钢板剪力墙的抗剪性能，扩充试验范围，本文采用通用有限元计算软件ABAQUS进行了数值分析.混凝土、钢板、加劲肋和栓钉采用C3D8R单元，即八结点线性六面体单元；钢筋采用T3D2单元，即两结点线性三维桁架单元.水平荷载的施加采用力和位移共同控制，过程与试验同步.基础底面采用完全固定的方式.墙体边界条件及加载形式如图9所示.

根据试验数据赋予模型截面特征和材料属性，混凝土本构采用塑性损伤模型，混凝土的抗拉和抗压应力应变曲线及混凝土抗拉和抗压损伤因子根据文献[9]取值.其中混凝土单轴抗压强度代表值取混凝土试块28 d立方体抗压强度的标准值，单轴抗拉强度代表值取抗压强度标准值的1/10，弹性模量取3.6×104 N/mm2，泊松比取0.2.钢材和钢筋本构采用双折线模型，钢材弹性模量取2.06×105 N/mm2，泊松比取0.3；钢筋弹性模量取2.1×105 N/mm2，泊松比取0.3.

为模拟钢板、栓钉与混凝土的共同工作，将栓钉嵌入到钢板和混凝土中，钢板和混凝土间采用罚摩擦；墙体混凝土与基础梁采用共节点连接，两侧钢板嵌入到基础梁中.在距墙顶0.005 m处创建加载点，并将加载点与墙顶表面耦合，用来施加水平荷载.基础梁、基础梁钢筋及墙体混凝土网格单元都取0.04 m，两侧钢板网格单元取0.02 m，栓钉网格单元取0.01 m.

4.2有限元计算结果与试验结果对比

通过以上建模所得的剪力墙有限元模型，破坏均由混凝土受拉侧达到最大拉应力引起，墙体达到极限承载力时受压侧混凝土未出现压碎，图10所示为试件W3破坏时的应力图，有限元模拟的破坏过程和试验结果比较吻合.

3个试件的有限元与试验骨架曲线对比如图11所示，曲线发展趋势相似，极限承载能力相近，但是屈服后位移相差较大，试验值大于有限元值.原因可能是试件基础与地槽锚固强度有限，在加载过程中试件会产生整体转动，且试件实际因为底部钢板局部屈服，混凝土受拉裂缝增大而破坏，以至于钢板在基础梁中出现滑移，墙体部分产生绕墙体受压侧角部的转动，对试件水平位移影响较大.由于有限元模型很难模拟这种大变形，导致试验位移与有限元位移相差较大.

表3显示了承载能力、延性系数的计算值与试验值的对比.可以看出极限承载力有限元值和试验值比值分别为1.02，1.12和1.01，两者吻合较好；耗能能力的功比指数试验值和有限元值也基本吻合，延性系数试验值与有限元值相差15%左右.

4.3极限抗剪承载力影响参数分析

为了考察影响双钢板剪力墙抗剪强度的因素，改变部分参数建立了W4～W13共计10个有限元模型，进行了参数分析，计算结果如表4与图12所示.

分析表4可知：

1）钢板厚度：W4比试件W1配钢率降低50%，而极限承载力同比减少12.82%；试件W5配钢率比W1增加50%，而极限承载力同比增加9.85%.增大墙体钢板厚度对墙体强度有一定的提高，但是增长幅度较小，这可能与核电站钢板剪力墙两边未设置充分约束以至不能充分发挥钢板的作用有关.

2）混凝土强度：双钢板剪力墙承载力随混凝土强度增加而增大，但是增加幅度较小，试件混凝土强度由C40提高到C50，极限承载力增加了4.33%；由C50提高到C60，极限承载力增加了9.54%.

3）轴压力分析：在试件W1基础上改变轴压比，取轴压力为100 kN，200 kN，编号为W8，W9.可以看出承载力随轴向力改变的幅度约为3%，轴压力对抗剪承载力的影响十分有限.

4）加劲肋分析：在试件W3基础上改变加劲肋含量（分别为30×3@120，80×3@120，50×3@60）对墙体进行有限元计算，编号为W10，W11，W12.W10加劲肋含量比W3减少66.7%，而极限承载力同比减少9%；试件W11加劲肋含量比W3增加60%，而极限承载力同比增加12.09%；试件W12加劲肋含量比W11增加25%，而极限承载力同比增加7.67%.可见抗剪承载力随加劲肋含量增加而提高，且提高幅度较大，增加加劲肋间距比增加加劲肋尺寸能更好地提高墙体抗剪承载力.

计算结果显示：有限元分析能较好地模拟试件的破坏，所得试件承载力、骨架曲线均与试验结果基本吻合.试件承载能力受配钢率影响较大，混凝土次之，轴压力最小，加劲肋含量对试件的承载能力、延性等影响较大.

5双钢板混凝土剪力墙抗剪承载力公式拟合

用于核电站安全壳中的双钢板混凝土剪力墙主要承受轴力、剪力和弯矩.但目前还没有抗剪承载力计算公式，设计时主要参考建筑结构中的钢筋混凝土剪力墙.如参考《高层建筑混凝土结构技术规程》采用有地震作用下偏心受压剪力墙斜截面受剪承载力计算公式（见式（1））[10]，计算本次试验的双钢板混凝土剪力墙试件斜截面抗剪承载力约为1 100 kN，约为试验值的4倍.其原因可能由于墙体混凝土太厚，其中没有钢筋约束，而外层钢板约束有限，因此受拉时混凝土极易开裂，造成抗剪强度较低.试验破坏模式也显示了与钢筋混凝土剪力墙的破坏有较大差别.因此双钢板混凝土剪力墙抗剪承载力不宜直接采用公式（1）进行计算.

V≤1γRE1λ-0.5（0.4ftbwhw0+0.1NAwA）+

0.8fyhAshshw0.（1）

分析核电站剪力墙模型可以看出，影响抗剪强度的因素包括：混凝土强度、钢板配置量、轴向荷载以及加劲肋.混凝土在抗剪过程中充分受力，而钢板不能充分发挥承载力.采用SPSS统计分析软件，仍然利用式（1）形式，增加加劲肋承载力项，将试验结果和有限元结果通过最小二乘法回归拟合，得到混凝土、轴向荷载、钢板以及加劲肋的分项承载力系数分别为0.61，0.12，0.06以及0.2.得到适合核电站双钢板混凝土剪力墙的斜截面抗剪承载能力计算公式如下：

V≤1γRE1λ-0.5（0.61ftbwhw0+0.12NAwA）+

0.06fyhAshHhw0+0.2fysAst.（2）

式中：γRE为承载力抗震调整系数；ft为混凝土抗拉强度；Ast为加劲肋截面面积；A为墙体的全截面面积；H为墙体高度；Aw为墙体腹板面积，矩形截面取墙体全截面面积；N为剪力墙轴向压力设计值，当N大于0.2fcbwhw时，应取0.2fcbwhw；fyh为钢板抗拉强度设计值；Ash为同一水平截面内钢板全截面面积；bw为墙肢腹板截面宽度，对矩形截面，取墙体宽度；hw0为墙肢腹板截面有效宽度，矩形截面时取墙体截面有效宽度；fys为墙中加劲肋抗拉强度设计值；λ为计算截面的剪跨比，当λ小于1.5时取1.5，大于2.2时取2.2，当计算截面与墙底之间的距离小于0.5hw0时，应按距离墙底0.5hw0处的弯矩值与剪力值计算.

由公式（2）计算的墙体斜截面抗剪承载力与试验结果和有限元结果对比如表5所示.由表5可以看出墙体的斜截面抗剪承载力的计算值与试验结果

6结论

本文从试验和有限元分析2方面对双钢板混凝土剪力墙进行抗剪强度研究，得到以下结论：

1）双钢板混凝土剪力墙具有良好的承载力、延性、耗能能力及抗侧刚度.由于模型钢板较薄，对混凝土约束有限，使得墙体的承载力增加有限.

3）栓钉间距影响钢板和混凝土之间的连接，能防止钢板面外局部屈曲，但对剪力墙承载力影响不大.通过设置加劲肋的构造措施，可以有效提高墙体的承载力与延性性能，但对延缓墙体裂缝出现影响不大.

4）双钢板混凝土剪力墙有限元分析结果与试验结果基本吻合，参数分析显示：混凝土强度、钢板厚度、轴向力、加劲肋构造影响剪力墙抗剪强度，其中加劲肋影响最大.

5）核电站双钢板混凝土剪力墙的受力特点和破坏机理与钢筋混凝土剪力墙差别较大，不宜直接应用钢筋混凝土剪力墙斜截面抗剪承载力计算公式.本文根据试验与数值计算结果，通过拟合分析，调整各项系数，提出了适合双钢板混凝土剪力墙斜截面抗剪承载力公式.

参考文献

[1]高宁.钢板混凝土结构在AP1000核电站中的应用[R].海阳：山东核电有限公司，2010：430-439.

GAO Ning. Steel reinforced concrete structure in the application of AP1000 nuclear power station[R]. Haiyang：SDNPC，2010：430-439.（In Chinese）

[2]WRIGHT H D， GALLOCHER S C.The behavior of composite walling under construction and service loading[J]. Journal of Constructional Steel Research，1995，35（3）：257-273.

[3]WRIGHT H D.The axial load behavior of composite walling[J]. Journal of Constructional Steel Research，1998，45（3）：353-375.

[4]罗永峰，李健，郭小农.双层钢板内填混凝土组合剪力墙滞回性能数值分析[J].湖南大学学报：自然科学版，2014，41（6）：57-62.

LUO Yongfeng，LI Jian，GUO Xiaonong.Numerical analysis of hysteretic performance of doblesteellayerconcrete composite shear wall[J]. Journal of Hunan University：Natural Sciences， 2014，41（6）：57-62.（In Chinese）

[5]聂建国，陶慕轩，樊健生. 双钢板混凝土组合剪力墙研究新进展[J].建筑结构，2011，41（12）：52-60.

NIE Jianguo，TAO Muxuan，FAN Jiansheng. Research advances of composite shear walls with double steel plates and filled concrete[J]. Building Structure， 2011，41（12）：52-60. （In Chinese）

[6]马晓伟，聂建国，陶慕轩，等.双钢板混凝土组合剪力墙压弯承载力数值模拟及简化计算公式[J].建筑结构学报，2013， 34（4）：99-106.

MA Xiaowei，NIE Jianguo，TAO Muxuan，et al. Numerical model and simplified formula of axial forcemoment capacity of composite shear wall with double steel plates and infill concrete[J]. Journal of Building Structures， 2013，34（4）：99-106.（In Chinese）

[7]侯春林，潘蓉.研究分析新版AP1000结构方面重要审评问题[J].电力勘测设计，2012（3）：75-80.

HOU Chunlin，PAN Rong. Research on critical reviews of the new version of the AP1000 structure[J].Electric Power Survey & Design， 2012（3）：75-80.（In Chinese）

[8]徐绩青.延性系数确定方法的探讨[J].水运工程，2004（9）：14-17.

XU Jiqing.Method of determining ductile coefficient[J].Port & Waterway Engineering， 2004（9）：14-17.（In Chinese）

[9]张劲. ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构， 2008，38（8）：127-130.

ZHANG Jing.Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure， 2008，38（8）：127-130.（In Chinese）

[10]JGJ 3—2010高层建筑混凝土结构技术规程[S].北京：中国建筑工业出版社，2010：79-86.