基于Richards-BP模型的地表沉降特征预测模型研究

任云志　周　飞　陆鹏宇

(贵州省交通规划勘察设计研究院股份有限公司　贵阳　550081)

基于Richards-BP模型的地表沉降特征预测模型研究

任云志周飞陆鹏宇

(贵州省交通规划勘察设计研究院股份有限公司贵阳550081)

摘要地下开采引起的地表沉降大致呈S形发展，最终趋于稳定状态，这能够运用生长曲线Richards函数进行预测分析。同时，又因为测量和外界存在不确定性和随机性，使得地表沉降也具有动态的特征。针对地下岩矿开采矿区地表沉降曲线与Richards预测模型曲线的相似性，分析了Richards模型在地表沉降预测中的适用性，提出通过Richards生长曲线模型预测矿区地表沉降的趋势性变形部分，利用BP神经网络模型降低地表沉降的随机性影响部分，提高模型预测效果。计算结果证明了其在地表沉降预测中的适用性和可行性。

关键词地表沉降预测模型Richards-BP神经网络模型

地下盐矿持续的开采会造成地表的大面积沉降，有必要在已有监测内容及数据的基础上，提前对该区的地表沉降进行预测，以便准确掌握地表移动特征及规律。地表沉降预测的目的在于根据实测获得矿区包含地表沉降、变形特征的数据以研究矿区地表沉降动态变化的规律，利用沉降预测模型，回归分析、拟合分析、迭代优化等方法确定预测模型的参数，以预计未来地表沉降量。目前，地表沉降预测常用模型主要有：Knothe时间函数模型、Kowalski广义时间函数模型、MMF模型、Richards模型等[1-3]，Knothe函数在预测地表沉降动态变化不够准确[4]，在利用MMF模型进行预测地表沉降时，需要给出曲线拐点后的部分实测数据，实测数据的个数会影响预测结果；Richards模型是一个含四参数的非线性回归模型，因其对多样性增长过程的描述能力强而受到学者关注[5]。本文采用Richards-BP模型进行预测矿区地表沉降，并通过实例应用说明其有效性和可行性。

1Richards-BP预测模型原理

地下采矿引起的地表沉降是一个复杂的四维时空问题，实践表明，采空区全过程的沉降-时间曲线呈S形[6]，见图1。图中OA段表示开采初期溶腔力学特征稳定，地表沉降大致呈线性增加；AB段表示随着地下矿的开采造成地表原稳定性被破坏，地表沉降量快速增加；BC段表示当开采量达到极限值时沉降尚未停止还有一定的增加；CD段表示开采结束后一定时间里，沉降速率减小，但持续缓慢增加，最终沉降极限值趋于稳定状态。采矿引起的地表沉降随时间推移呈趋势性变形，又因为测量和外界不确定性和随机性的存在，使得地表沉降具有偶然误差，因此通过Richards生长曲线模型预测出矿区地表沉降的趋势性变形部分，利用BP神经网络模型降低地表沉降的随机性影响部分，提高模型预测效果[7]。

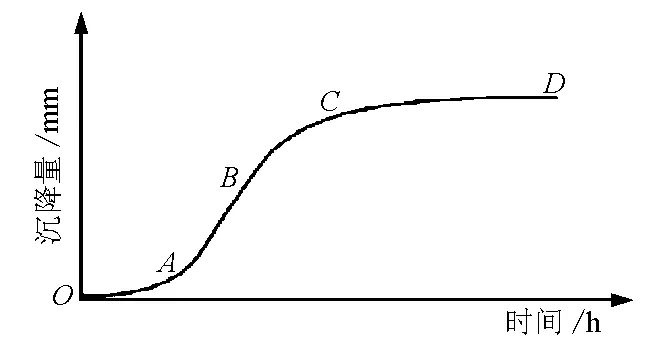
图1　矿区地表沉降的发展过程

1.1Richards预测模型

Richards生长曲线模型的一般方程为

(1)

式中：S(t)为某监测点在时刻t的沉降量，t为沉降值S(t)与首次观测的时间间隔；Sm为最终沉降量；A为初始沉降值参数；k为沉初始沉降速度参数；m为曲线形状参数。

Richards模型的特点有：①不过坐标原点；②有界性；③单调性；④满足固结度条件；⑤良好的可塑性：当m取值不同时，其对应的曲线形状也发生相应变化，见图2。当m=0时，式(1)变换为MitscherlichBrody模型；当m=0，A=1时，式(1)变换为Knothe模型；当m=2/3时，式(1)变换为vonBertalanffy模型；当m→1时，式(1)变换为Gompertz模型；当m=2时，Richards模型变换为Logistic模型。

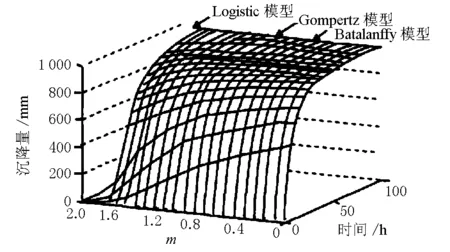
图2　Richards曲线模型的可塑性

1.2BP神经网络模型原理

BP神经网络是一个高度复杂的非线性系统，具有自组织、自适应和自学习能力的特点。模型输入信息通过正向传播，将误差反向传播，逐层修改各层神经元的权值和阈值，减少误差，如此迭代直到输出满足要求为止。本文采用S形传递函数又称非线性连续型模型，其函数为

(2)

本文采用3层BP网络，其模型输入层第个节i点的输入为

(3)

式中:xi为神经网络的输入，即Richards模型的计算结果；θi为第i个节点的阈值。

对应的输出为

(4)

式中：wjk为隐含层的权值；θk为第k个节点的阈值。

1.3Richards-BP神经网络组合预测网络

首先，利用实际沉降监测数据拟合预测矿区地表沉降的Richards曲线模型，预测出矿区地表沉降变形趋势；然后，运用BP神经网络模型对Richards预测模型预测结果的绝对误差进行处理，即以Richards模型预测的绝对误差作为BP神经网络模型的输入和输出值，运用BP神经网络模型对预测误差进行修正，得出Richards-BP修正后的模型预测误差，以提高模型的预测精度。

2预测模型的应用分析

2.1矿区地表沉降预测算例

研究对象为某水溶法开采矿区岩盐矿地表沉降监测工程，该区地表沉降监测始于2007年7月，选取其中L1-04的连续11期的数据作为分析对象。经过统计计算得出其时间变量t与地表沉降量S(t)地表沉降已知数据见表1。为了便于计算，对地表沉降量S(t)的符号进行了取绝对值处理。

表1　时间变量t与地表沉降量S(t)数据表

运用Origin对几种预测模型进行预测值拟合，得出预测与实测沉降值曲线，见图3，其相应精度指标值见表2。

数据表明，Richards预测模型的预测值与实测值的相关性最好，预测精度较好，虽然少量沉降预测值较大，但对于工程安全来说是有利的。

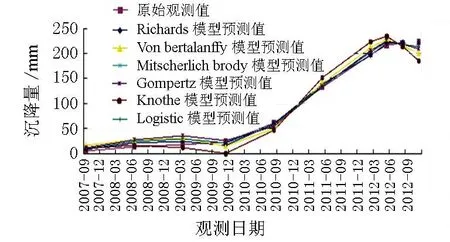
图3　几种模型预测值与实测沉降值曲线

项目RichardsV-B模型M-B模型GompertzKnotheLogistic预测模型预测误差值/mmReducedChi-Sqr31.790162.3401037.078103.030325.86051.610Root-MSE5.63912.74132.20410.15018.0517.184相关系数R0.997940.988830.926290.992920.926240.99646

2.2矿区地表沉降预测值修正

以L1-04号点的23期地表沉降变形监测数据为例，运用Matlab进行编程对BP神经网络模型进行分析计算，输入节点数为4，隐含节点数为9，输出节点数为1，其中取学习率为λ=β=0.05，动量因子η=δ=0.9，误差平方和E=1×10-6，其输入样本值P与目标值T为：T=[3.2,8,6.1,-5.4,-0.8,5.1,-2,3.4,0.4,-1]T，P=[2.6,3.3,1.7,2.8;6.9,8.1,7.6,6.2;6.7,5.4,6.6,4.3; -5.7,-4.6,-4.4,-3.7;0.5,-2,-1.1,1.1;3.8,3.9,6.1,5.9;-0.9,-1.2,-0.7,-3.5;2.7,2.5,4.3,4.5;2.2,-0.2,-0.8,0.1;0.5,-2.7,-0.1,-1.2]。利用Richards预测模型预测出L1-04号点的沉降值，再通过运用Matlab进行编程，分析Richards预测误差值的随机部分，修正Richards预测模型的预测误差值，得到Richards-BP组合预测模型预测值，以提高预测的精度，其均方差MSE=4.906，2种模型的精度见表3。

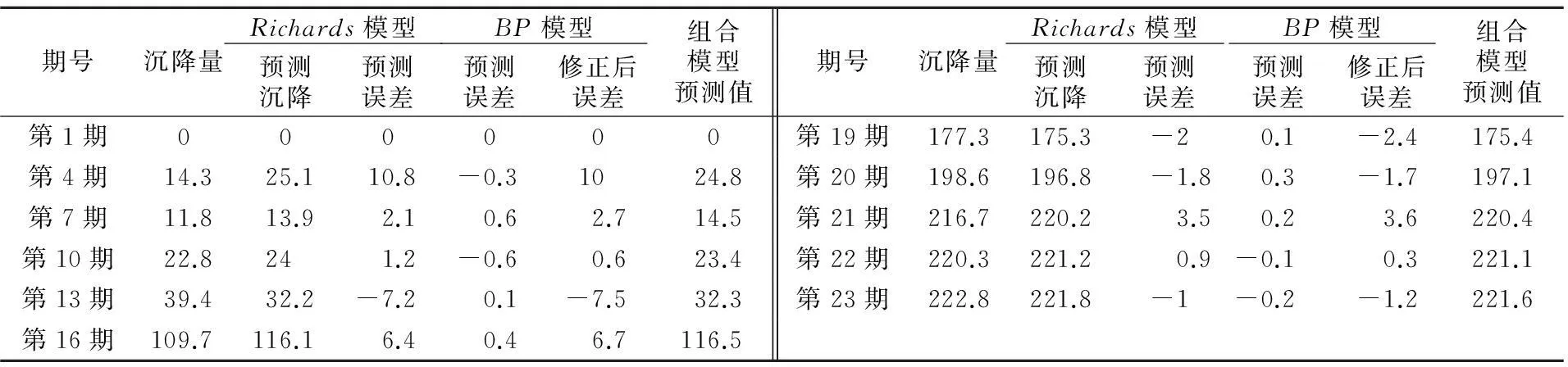
表3　Richards-BP组合模型预测精度分析　mm

通过Richards-BP组合预测模型得出的预测值，很好地对Richards预测模型中的随机变化部分进行了平滑处理，其与实际沉降值曲线见图4。

图4　Richards-BP模型预测值与实际沉降值曲线

3结论

针对传统岩矿开采矿区地表沉降预测模型预测需要曲线拐点数据及预测动态变化不够准确的不足，本文分析了Richards模型在地表沉降中的预测，得出Richards模型是几种模型中预测精度较好的，相关系数R为0.997 94，均方根误差root-MSE为5.639。在计算得到Richards预测模型的误差后，再运用BP神经网络对Richards模型预测误差进行处理分析，得出更加精确的Richards-BP模型预测值，得到组合模型预测值的误差方差值为4.906, 取得了较好的预测效果，表明利用该模型进行地表沉降预测是有效的和可行的。

参考文献

[1]王军保，刘新荣，李鹏,等.MMF模型在采空区地表沉降预测中的应用[J].煤炭学报，2012，37(3)：411-413.

[2]朱文兵.软土地基桥梁桩基础沉降测试及预测岩层[D].长沙：中南大学，2011.

[3]赵霞.Richards曲线模型在地基沉降预测中的应用[J].贵州大学学报:自然科学版，2011，28(3)：103-105.

[4]崔希民，缪协兴，赵英利,等.论地表移动过程的时间函数[J].煤炭学报，1999,24(5)：454-456.

[5]包太，税月.MMF生长模型在隧道监测数据分析中的应用研究[J].贵州大学学报:自然科学版，2009,26(4)：131-133.

[6]王正帅，邓喀中.采动区地表移动沉降预测的Richards模型[J].岩土力学，2011，32(6)：1664-1666.

[7]高阶，王建伟，李琳娜.基于Richards-BP审计网络的交通运输碳排放量组合预测模型[J].长安大学学报:自然科学版，2013，33(4)：100-103.

收稿日期：2014-10-21

DOI10.3963/j.issn.1671-7570.2015.01.032