离散元法在贵阳某层状岩质边坡稳定性分析中的应用

谭玉强　段富凯　田何林

(1.贵州交通岩土工程有限责任公司　贵阳　550018；　2.贵州省交通规划勘察设计研究院股份有限公司　贵阳　550018)

离散元法在贵阳某层状岩质边坡稳定性分析中的应用

谭玉强1,2段富凯2田何林1,2

(1.贵州交通岩土工程有限责任公司贵阳550018；2.贵州省交通规划勘察设计研究院股份有限公司贵阳550018)

摘要以实际工程为背景，介绍了贵阳某层状岩质边坡的特点，分析了边坡的破坏机理及破坏模式，采用二维离散元法对该边坡进行了稳定性分析，指出了在前缘临空情况下，边坡容易发生滑移-拉裂破坏。模拟计算结果与理论分析相符，说明用离散元法分析层状岩质边坡的稳定性是可行的。

关键词层状岩质边坡离散元法变形机理破坏模式

1工程概况

(1) 边坡概况。贵阳市乌当区云锦庄至开阳公路其边坡自然坡度约32°，φ=18°，边坡沿主滑方向长约100m，宽约150m，滑体厚度约13.50m，滑体面积约1.35×104m2，体积约1.3×105m3，边坡地形陡，边界裂缝明显，平面上呈圈椅状。

(2) 边坡的岩土构成。根据地质调绘及钻探结果，自上而下分述如下：

①碎石土覆盖层。褐、褐黄色，碎石成分为砂质泥岩，一般粒径为50～100mm，最大粒径可达150mm，含少量植物根系，结构稍密，场区均有分布，揭露厚度为0～10.80m。

②基岩。为寒武系下统明心寺组(∈1m)薄层状砂质泥岩，根据风化程度分为：a)全风化层。灰白、土黄、灰黄色，泥质结构，薄层状，岩质极软，节理、风化裂隙极发育，岩体破碎，呈碎裂结构，岩芯呈土状、砂状，厚度为1.10～10.80m，场区均有分布；b)强风化层。灰、灰白、浅灰色，泥质结构，薄层状，岩质软，节理、风化裂隙极发育，岩体破碎，呈散体结构，岩芯呈砂状、块状，厚度为0～8.40m，场区均有分布；c)弱风化层。灰、深灰色，泥质结构、薄层状，岩质较硬，构造节理较发育，岩体较完整～完整，岩心以柱状为主、少许块状，该层埋藏较深。

处理后复核土层的内摩擦角和粘聚力计算路基的整体稳定性，采用简化Bishop法分析计算得路基整体稳定性系数为1.324，路基整体稳定。由此可见，经过处理后的软基大大提高了其物理力学参数，增强了路基的整体稳定性。

2.32种方法的对比分析

以处理40m长计算，各工程对比见表1。

表1　相关材料需求量对比

通过以上2种方法的处理分析后，可见采用抗滑桩处理时可节约路基填筑材料方量，水泥及砂石量均较CFG桩处理时要少，根据相关工程造价估算抗滑桩较CFG桩节约约40%。在一定程度上节约了路基填筑成本及土地。从另一个角度来考虑，填石路基按1∶1.1～1∶1.3的整体稳定性较1∶1.5～1∶2时要差得多，整体稳定性则是CFG桩较理想。

3结论

(1) 对于存在浅埋软土夹层的路基，其稳定性受软土夹层影响，且以通过软土夹层底面的滑动面安全系数最小，实际工程中应以此作为工程稳定性的控制因素。

(2) 通过收坡避让软基虽然节省了土石方量，但在实际工程中应根据前后土石方需求控制，达到经济合理利用废方。

(3) 根据软基处理宽度可综合考虑2种方法的优缺点及其适用性，在处理软基较宽时，考虑抗滑桩比较经济；而软件宽度较小时则选择CFG桩较为稳定合理。

参考文献

[1]赵明华,刘煜,曹文贵.软土路基沉降发展规律及其预测[J].中南大学学报,2004,35(2):157-161.

[2]何广讷,肖专文,肖道一,等.软土夹层地基上土堤的稳定性分析[J].沈阳建筑工程学院学报,1993, (9):118-125.

[3]段姣娇.公路工程软土路基施工技术[J].现代公路,2012(23):150-151.

[4]莫海鸿,杨小平.基础工程[M].北京:中国建筑工业出版社, 2008.

2理论分析

(1) 边坡现状。边坡范围内地面裂缝明显，主要集中在边坡后缘，多为拉张裂缝，裂缝走向与滑动方向近于垂直，其中最大裂缝宽度达20cm，垂直位移0.15～0.20cm，长约67m；南侧裂缝多呈羽状排列，与滑动方向斜交，自北东向南西消失；滑区中下部裂缝较少，多呈弧状；坡脚处出现一条弧形裂缝，当前部荷载去除之后，该边坡将可能产生滑动破坏，且该边坡属于缓倾层状岩质边坡。

(2) 变形机理。该边坡符合前面所讨论的缓倾坡的破坏机理。该边坡目前处于蠕变过程，当坡前荷载去除之后，在自重作用下，边坡岩体将沿下伏软弱面向坡前临空方向产生滑移-拉裂破坏。

(3) 破坏模式。该边坡将会发生阶梯状的平面滑动破坏。

(4) 判别依据。依据文献[1]滑移-拉裂的判别公式进行判别。

(1)

(2)

(3)

由工程概况可知：L=100m，b=150m，φ=18°，α=32°。

计算可得：A=0.55，B=33.7°，β0=38.4°。

又由工程概况可知β=36°，故该滑动破坏是可能的。

3数值模拟计算

采用2d-block离散元数值模拟软件对该边坡的变形失稳机理及破坏模式进行模拟计算。

(1) 离散元法基本原理。离散单元法是将研究区域划分成单元，各单元因受节理等不连续面控制，一个单元与其邻近单元可以接触，也可以分开，单元之间相互作用的力可以根据力和位移的关系求出，个别单元的运动则完全根据该单元所受的不平衡力和不平衡力矩的大小按牛顿运动定律确定[2]。

物理方程：力和位移间的相互关系。离散单元法采用了力-位移关系，并且认为这个关系是可逆的。2块体相互作用的力与接触块体之间的叠合量有关(见图1)，假定块体间的法向力Fn正比于它们之间法向“叠合”un，即

Fn=knun

(4)

式中：kn为法向刚度系数。

“叠合”是计算时假设的一个量，将其乘上一个比例系数作为法向力。对于确定的法向力，可以增大kn的值、减少un的值，而使二者的乘积等于相同的法向力。

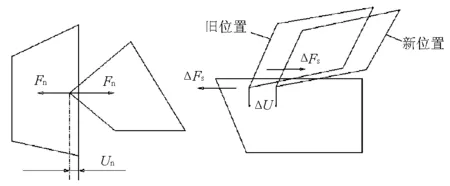
图1　叠合量与作用力之间的关系

块体所受的剪切力与块体运动和加载的历史途径有关，所以宜用增量的形式来表达。设2块体之间的相对位移为Δus，则

(5)

式中：kn为节理的剪切刚度系数。

(2) 模拟参数取值见表1。

表1　模拟参数取值表

(3) 数值模拟计算成果及分析。数值模拟计算成果见图2～图5。

图2平均主应力图图3形心速度图

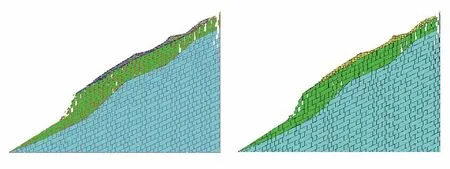
图4块体位移图图5破坏效果图

数值模拟成果分析。

(1) 由图2可见，当前部荷载去除之后，坡体平均主应力发生了明显的变化，前缘应力释放，中部及后部应力均做了调整，沿层面向坡脚移动。

(3) 由图3可见，当前部荷载去除之后，坡体产生了形心速度，前缘形心速度较大，中部及后部受前部块体的影响，加速度较小，但加速度方向均沿层面指向坡脚。

(3) 由图4可见，当前部荷载去除之后，坡体上的块体产生了明显位移，前部和后部位移较大，中部受前部块体的影响，位移较小，但位移方向均沿层面指向坡脚。

(4) 由图5可见，当前部荷载去除之后，坡体上的块体由于前缘临空，前部块体产生滑移，中部及后部发生了明显的拉裂破坏。

综上，当坡前荷载去除之后，边坡岩体将沿下伏软弱面向坡前临空方向滑移，并使滑移体拉裂解体。软弱面向临空方向倾角大于岩层的内摩擦角，一旦该面被揭露，上部坡面岩体临空，破坏了原坡体的平衡条件，导致上覆岩土体失去支撑，造成前缘产生明显的滑移，后部产生拉裂，坡体由前部向后部逐步解体的滑移-拉裂破坏，破坏模式为平面滑动，且滑面为折线形[3]。结果与前述的理论分析一致。

4结论

(1) 本文采用离散元法，利用2d-block软件对贵阳某层状岩质边坡进行了稳定性分析。将块体平均主应力、形心速度、块体位移发生明显变化作为失稳判据，由对应边坡块体的破坏效果图确定滑面及破坏形式。根据模拟计算结果对比分析表明，应用该方法对层状岩质边坡进行稳定性分析是一个有效的方法。

(2) 当边坡的结构面参数较低，且岩性较好时，可以将其视为刚体来选取计算参数进行模拟计算，该方法计算效率高，结果可靠[4]。

(3) 采用二维2d-block离散元数值模拟软件分析层状岩质边坡的稳定性，可以看到边坡破坏过程中的块体平均主应力、形心速度、块体位移及破坏效果，对有效、快速、直观地判断层状岩质边坡破坏机理及破坏模式具有很好的指导意义。

[1]张倬元,王士天,王兰生.工程地质分析原理[M].2版.北京:地质出版社,1994.

[2]黄润秋.中国西南地壳浅表层动力学过程与工程环境效应研究[M].成都:四川大学出版社,2002.

[3]谭玉强.层状岩质边坡稳定性评价理论与支护设计方法研究[D].贵阳:贵州大学,2009．

[4]宁宇.应用离散元强度折减对复杂边坡进行稳定性分析[J].岩土力学,2007，28(S):569-574.

收稿日期：2014-09-10

ResearchonSlopeStabilityAnalysisofALayeredRock
SlopeinGuiyangUsingDistinctElementMethod

Tan Yuqiang1,2， Duan Fukai2，TianHelin1,2

(1.GuizhouTransportationofGeotechnicalEngineeringCo.,Ltd.,Guiyang550018,China;

2.GuizhouTransportationPlanningSurvey&DesignAcademeCo.,Ltd.,Guiyang550018,China)

Abstract：Based on the background of practical engineering, characteristics of some layered rocky slope in Guiyang are introduced. The deformation mechanism and destruction are analyzed in theory to the slope.The method of 2D discrete element is applied to the slope stability analysis．It is pointed out that the slope is easy to cause sliding-tensile failure under the condition of the front opening. The simulation results are in conformity with theoretical analysis. It shows that element method is feasible for the analysis of layered rock slope stability. This method is a rational and efficient stability analysis method and is worth using in similar projects．

Key words:layered rock slope; distinct element method; deformation mechanism; destruction pattern

DOI10.3963/j.issn.1671-7570.2015.01.021