双馈异步电机转子匝间短路的建模与稳态分析

双馈异步电机转子匝间短路的建模与稳态分析*

李俊卿，王志兴

(华北电力大学 电气与电子工程学院，河北 保定071003)

摘要：理论上分析了发生转子匝间短路，定子侧电流所含的谐波成分。基于MATLAB/Simulink中的S函数，以多回路理论为基础建立了双馈电机的数学模型，对双馈异步电机正常情况和转子发生匝间短路这两种情况下进行了仿真。分析了电力电子器件对转子侧电流谐波的影响，对定子侧线电流进行了傅里叶分析。通过傅里叶分析可以得到判别转子匝间短路的依据，由仿真试验数据分析可以得到与理论分析相一致的结果，说明了基于S函数的多回路模型的仿真试验是可行的。

关键词：双馈异步电机； 匝间短路； 多回路； S函数

基金项目：* 河北省自然科学基金资助项目(2014502015)

通讯作者：王志兴

中图分类号：TM 346+.2文献标志码： A

收稿日期：2015-04-02

Model and Steady-State Analysis of Rotor Inter-Turn

Short-Circuit Fault in DFIG

LIJunqing,WANGZhixing

(School of Electrical and Electronic Engineering, North China Electric

Power University, Baoding 071003, China)

Abstract：The analysis of the current harmonic components of the stator side contained under rotor winding inter-turn short-circuit was done. The multi-loop math model was built for rotor winding of DFIG under normal and inter-turn short-circuit fault conditions. The simulation was carried out,using S-Function in Simulink,and deeply analysis for the results by FFT analysis was done,the influence of power electronic devices was also considered.Base on the analysis the rotor winding inter-turn short-circuit could be easily found.The simulation result accorded with the theoretical analysis,it showed the simulation base on S-Function was reliable.

Key words： doubly fed induction generator(DFIG)； inter-turn short-circuit； multi-loop； system function

0引言

双馈式风力发电机由于其良好的性能，已广泛应用于风力发电中。双馈异步电机故障大致分为三类： 匝间短路故障、轴承故障及气隙偏心故障[1]，双馈异步电机的转子匝间短路是电机的常见故障之一，如果长期运行可能会造成绝缘损坏，从而引发更加严重的故障，轻则停机停产，重则威胁电力系统的安全运行。如果在故障发生的早期能及时发现，合理安排检修以及事后的维修工作，可以有效地防止潜在危害的发生，所以研究转子匝间短路具有重要意义。

研究转子匝间短路首先就要建立其相应的数学模型，并且进行相关的仿真试验，通过对试验结果的分析找出转子匝间短路的判据。文献[2-6]主要介绍了双馈电机不同的建模方法。文献[7]研究了发电系统外围不同的控制策略对于转子匝间短路的影响。文献[8]介绍了转子绕组匝间短路时采用小波分析来判别故障。文献[9]介绍利用希尔伯特-黄来判别故障电流和正常电流，从而识别故障，与小波分析作用类似。文献[10]基于有限元的方法对转子匝间短路时的负序电流进行检测，从而找出故障发展趋势。文献[2,5,10-11]研究匝间短路仅仅考虑了电机本身，没有考虑变流器等电力电子元件的影响。文献[7]虽然计及了控制系统的影响，但由于轻微匝间短路属于早期故障且故障特征量不是十分明显，所以需要采用比较精确的双馈异步电机的数学模型，而大多数基于坐标变换思想的数学模型比较适合研究正常情况下电机，在匝间短路故障时，坐标变换的思想可能会带来误差。

本文在三相坐标系下建立了双馈异步电机正常情况和转子匝间短路情况下的数学模型，利用MATLAB/Simulink中S函数实现该数学模型，并且考虑到电力电子器件对转子匝间短路的影响，由于匝间短路会引起转子三相电流不对称，并且伴随谐波的产生，可对仿真结果进行傅里叶分析来研究转子匝间短路。

1定子侧谐波分析

(1)

式中：φ——以转子坐标表示的机械角度；

t——时间；

N——短路匝数；

I——短路电流有效值；

p——极对数；

υ——谐波次数；

kwv——短路匝绕组系数；

ω2——转子电流角速度。

假设θ表示以定子坐标表示的机械角度，则f(φ,t)转换到定子侧的表达式为

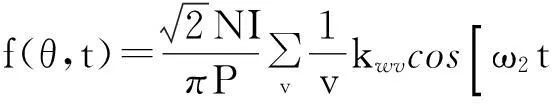
(2)

式中：s——转差率。

其在定子线圈感应的电动势为

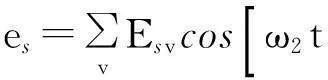
(3)

式中：Esv——定子侧感应电动势v次谐波幅值。

由此可以看出在发生转子匝间短路时，在定子侧感应出电流的谐波成分为

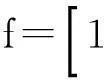
(4)

式中：f2——转子侧电流频率。

2数学模型的建立

2.1S函数

S函数可以与Simulink方程求解器相互作用，这种功能与模块库自有的模块功能十分类似，使用S函数编写的程序可以封装和移植，使用高效方便。S函数可以用M、C以及C++等多种语言编写，这样可以把程序代码封装为模块，极大地扩展了Simulink的使用范围。本文采用多回路理论建立双馈异步电机转子匝间短路的数学模型，利用S函数方便的矩阵操作特性对多回路模型进行仿真。S函数模块的数学关系如图1所示。Simulink大致分为初始化阶段和仿真循环阶段，到仿真循环结束即输出结果。

图1S函数的输入输出

2.2多回路数学模型

多回路理论已成功运用在电机内部故障问题上。以下建立了双馈异步电机的多回路数学模型。为方便理论分析，又不失工程实际的要求，做如下假定[12]： (1) 不考虑铁心的磁滞、涡流损耗，双馈异步电机气隙均匀。(2) 转子匝间短路前在正常状态下运行。

本文对双馈异步电机进行了多回路数学建模，电机定子绕组三角形连接，并联支路数为2，转子星形连接，并联支路数为1，匝间短路发生在转子a相，如图2所示。

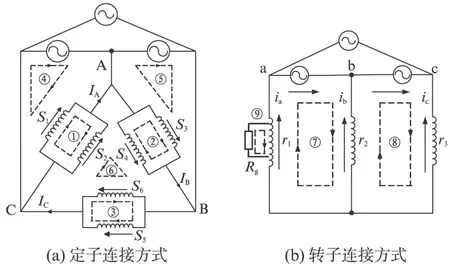
图2　双馈异步电机三相绕组连接图

正常情况下交流电机的多回路模型为

U=pLI+RI

(5)

式中： U、I——9行1列的定转子电压、电流矩阵；

R——9行9列的电阻矩阵；

L——9行9列电感矩阵，包括定子自感和互感、转子自感和互感以及定转子之间的互感。

为了处理方便，特把支路方程转换为回路方程[12]，转换矩阵H如下：

(6)

支路电流和回路电流的关系为

I=HTI′

(7)

把支路方程转化为回路方程，可得到如下数学模型：

HU=HRHTI′+HLHTpI′+HpLHTI′

(8)

把式(8)化简为状态方程如下：

pI′=(L′)-1U′-(L′)-1R′I′=AI′+B

(9)

其中： HU=U′；

HLHT=L′；

HRHT+HpLHT=R′；

A=(-L′)-1R′,B=(L′)-1U′。

采用MATLAB/Simulink中S函数来求解式(9)的变系数微分方程，求得回路电流的稳态值。当发生转子侧匝间短路时，只是在转子侧增加了一个回路，相应在式(5)各个矩阵增加一阶。设过渡电阻Rg=0，回路的电压方程如下：

0=pψg+rgIg-rgia

(10)

式中： Ig——流过短路回路的电流；

ia——短路所在支路电流；

rg——短路匝电阻。

在匝间短路时，重新求解方程，可得到新的回路电流值，经逆变换得出支路的电流值。根据式(10)可以仿真不同程度的匝间短路，得出不同的结果。

2.3仿真模型的建立

以式(5)～式(10)为数学模型，可以基于S函数实现此模型的仿真试验。多回路模型的重点在于各个回路电感值的计算。本仿真试验包括自感和互感两部分，其中定子各个支路的自感和互感为不变值，转子各个支路的自感和互感也为不变值，而定转子之间的互感为时变量，随着转子位置的不同而时刻变化。总之，式(5)中的电感矩阵L为时变矩阵，这就需要求解变系数微分方程，而S函数方便的矩阵操作特性，可以求解变系数微分方程。当电机正常运行时，回路电流为状态变量，以状态变量作为输出量，此状态方程为8输入8输出的系统；当电机转子匝间短路时，会多出一条回路，此时为9输入9输出系统，仿真如图3所示。

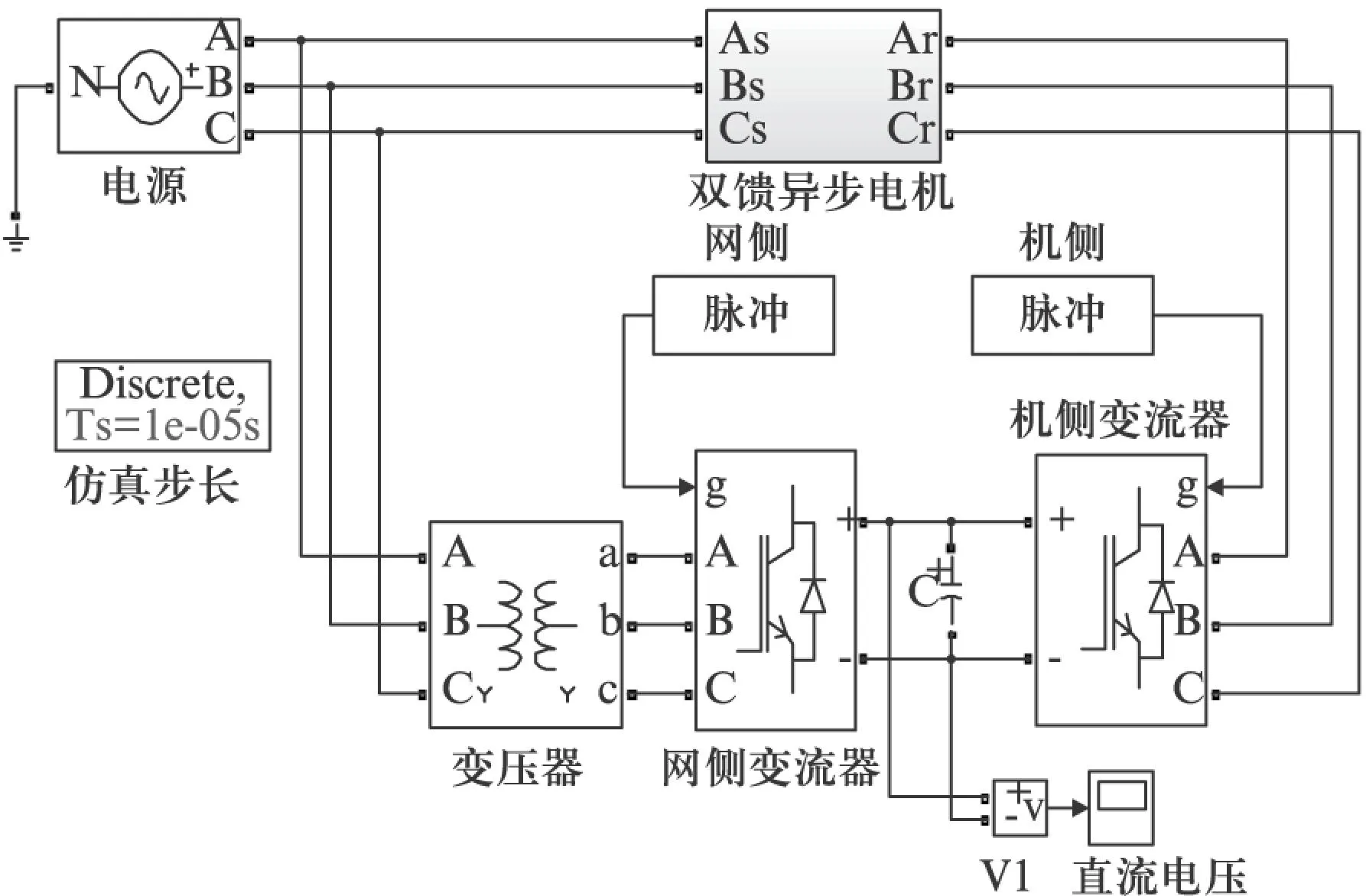
图3　仿真图

图3中子系统双馈异步电机即为双馈异步电机的转子匝间短路的模型，三相电压输进双馈异步电机子系统，首先物理量转为数字量，然后再作为S函数模块的输入，以IGBT代替变流器，脉冲为内部发生。以下对一台型号为YR132M-4的双馈机进行了仿真，模拟多回路模型下的转子匝间短路。双馈机的基本参数如下： 额定功率5.5kW；额定电压380V；额定频率50Hz；极对数2；定子槽数36；转子槽数24；定子并联支路数2；定子每支路串联线圈数6；定子每线圈匝数37；定子每支路阻值4.04Ω，转子并联支路数1；转子每支路线圈数8；转子每线圈匝数12；转子每支路阻值0.83Ω，在并网条件下，转子发生匝间短路。在正常和a相5匝短路时进行仿真。

3仿真结果与分析

转子在正常情况和发生5匝匝间短路情况下的仿真结果如图4所示，两种情况下的电流幅值如表1所示。

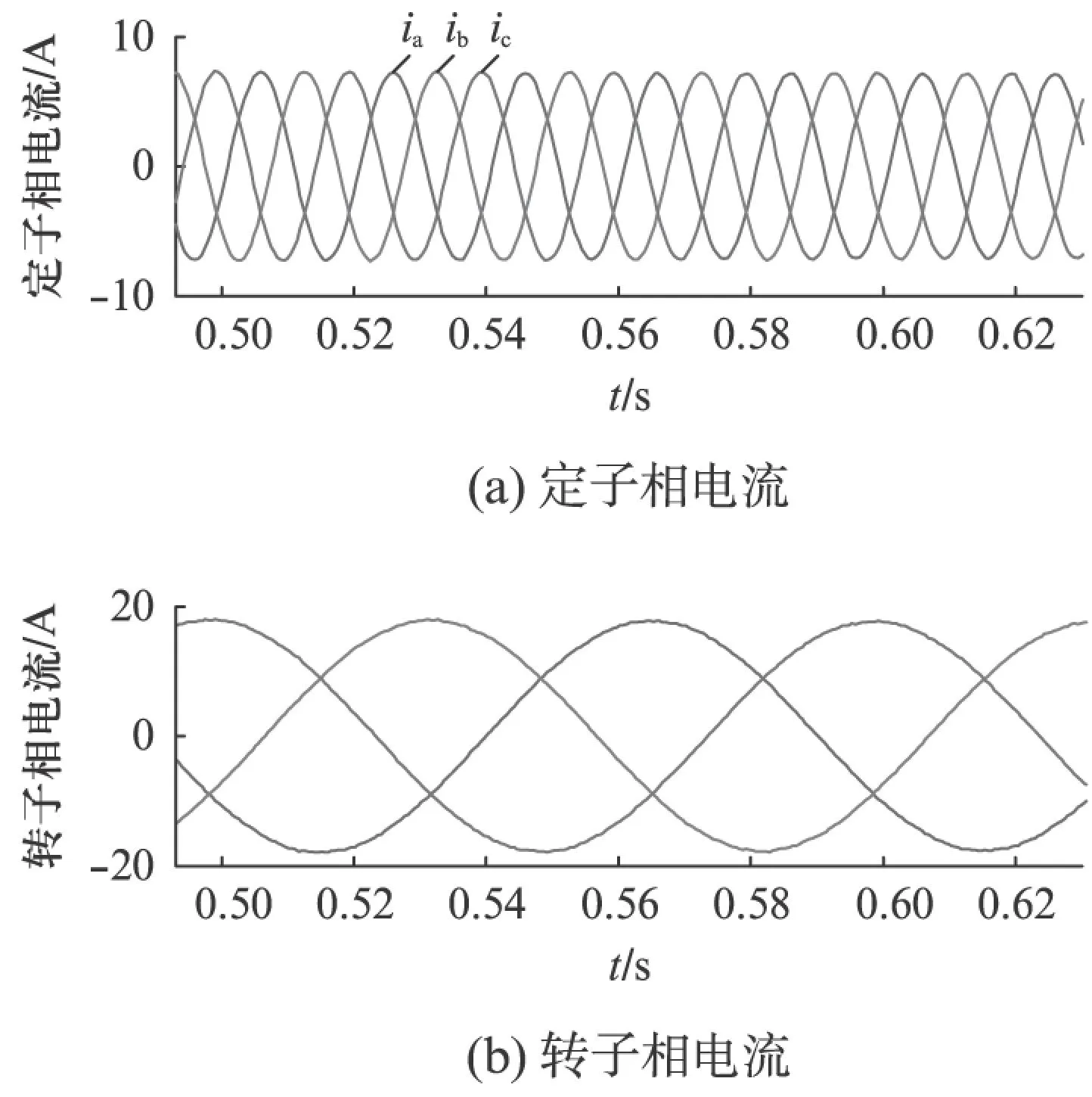
图4　正常情况电流波形

相电流正常情况5匝短路ia/A18.9421.05ib/A18.9420.61ic/A18.9419.60

由图4及表1可以看出，在正常情况下定转子三相电流对称。当发生转子5匝匝间短路时，转子侧三相电流出现不对称。三相电流幅值都有所增大，短路相a相电流幅值增幅最大，这是因为短路电流的存在，bc两相电流幅值也有所增大，而定子侧则会出现谐波。匝间短路时仿真波形如图5所示。

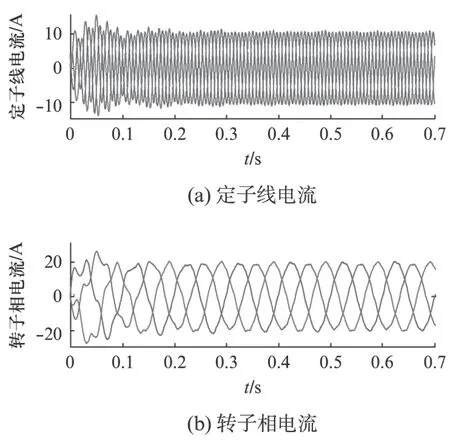
图5　匝间故障时0～0.7s电流波形

图5为转子匝间短路时0～0.7s的定转子电流图形。图6是0.5～0.62s时的定转子电流波形图，其中定子为线电流，定子侧改成线电流表示，为方便观察，转子为相电流。图5起始阶段的振荡是程序运行的未收敛阶段，之后进入稳态才表示正确的数值。由图5可知定子侧线电流发生了明显的周期性波动，由外包络线可以观察出来。转子侧的电流波形明显发生不对称，并且含有谐波成分。由仿真和理论分析可知电力电子器件会给转子侧带来一部分高频谐波[13]，而电流幅值不对称则主要由匝间短路引起。

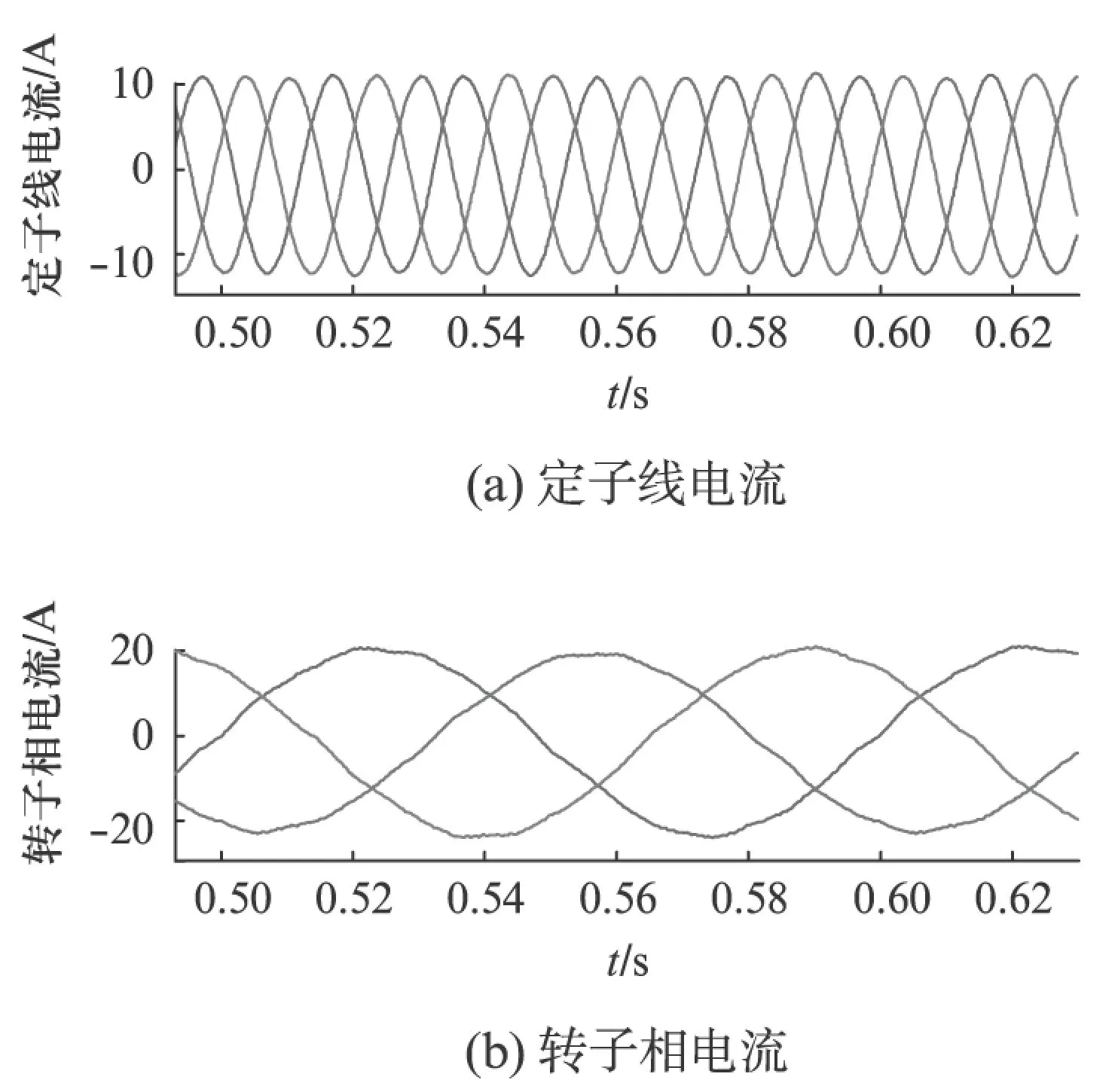
图6　匝间故障时0.5～0.62s电流波形

由理论分析可知，在发生转子匝间短路时会在定子侧感应出特定频率谐波。以下在开关频率为1200Hz时对定子侧线电流Iab进行傅里叶分析，分析结果如图7所示。

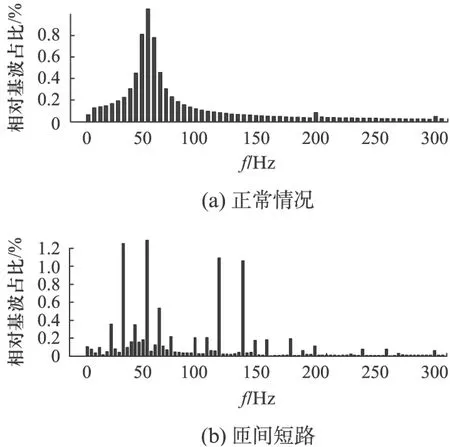
图7　傅里叶分析

由图7可知,正常情况下定子侧电流谐波含量相对较少，且集中在基波附近；当发生转子匝间短路时，定子线电流中30、70、110及130Hz变化明显，尤其是30、110及130Hz谐波变化十分明显。图7(b)中30Hz谐波相对于基波的含量为2.87%。

4电力电子器件的影响

由于开关频率等因素的影响，电力电子器件会给转子侧带来高次谐波，尤其当开关频率较低时，会使得转子侧电流谐波含量变大，仿真结果如图8所示。

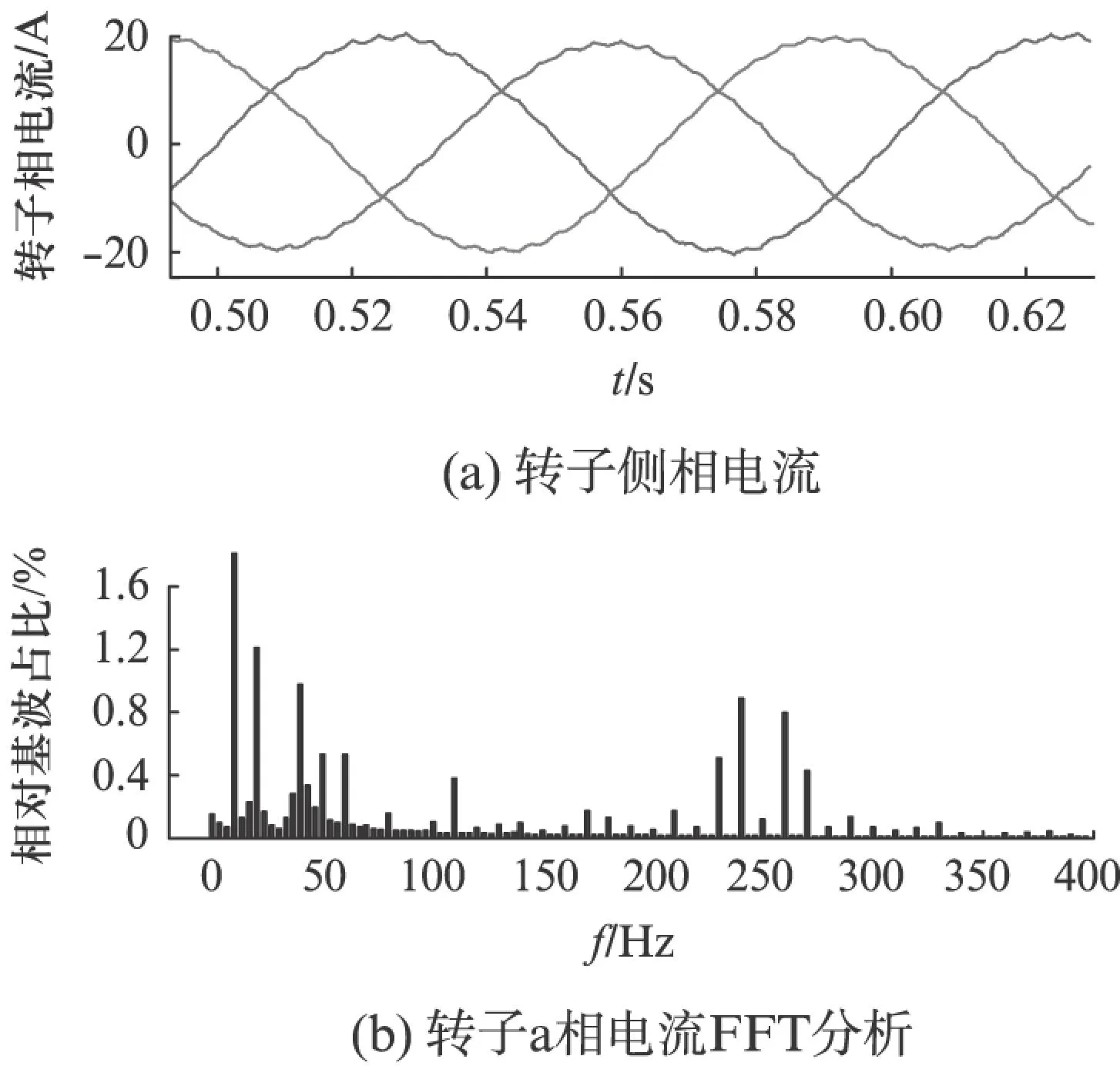
图8　转子电流波形及FFT分析

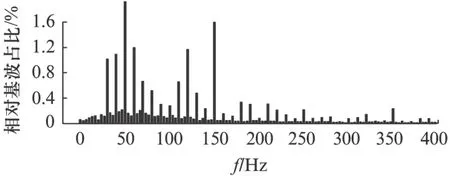
图9　定子线电流FFT分析

图8开关频率500Hz时，测得的转子电流波形及其相应的傅里叶分析。由于此时开关频率较低，由图8可知除了10Hz的基波电流以外出现了部分高次谐波，可见电力电子器件对转子侧谐波影响是比较明显的。如果以转子侧电流谐波ksf作为检测量[14]，k=3,5,7…，f为基频，s为转差率，本仿真f=10，s=0.2，那么会对在100～300Hz期间的谐波测量结果产生干扰，甚至会造成误判。由此看出以转子侧电流谐波来检测转子匝间短路容易产生误判，但这些高次谐波并不会对定子侧电流带来干扰，定子侧影响可以忽略不计。由图9可看出，30、70、110、130及150Hz等故障特征量仍然含量比较大，与开关频率较大时相比，定子侧出现了其他频率的谐波，如120Hz。在仿真试验时，应把开关频率设置高一点，避免因电力电子器件引入谐波。现实生产中要考虑实际情况合理选择开关频率，较低会出现谐波，较高可能会增大开关损耗和降低晶闸管寿命。

5结语

由以上理论分析和仿真试验结果分析可得出以下结论：

(1) 建立了基于S函数的多回路混合仿真模型，电机模块和其他模块交互作用，为整个发电系统下研究匝间短路奠定基础。

(2) 当转子发生匝间短路时，其相电流幅值三相不对称，三相电流较正常情况下幅值均增大且故障相电流增大最明显。

(3) 转子匝间短路会在定子侧电流引入谐波，使得定子线电流发生周期性波动。

(4) 研究了电力电子器件对转子侧电流谐波的影响，以转子电流谐波为检测量容易产生误判。如果以转子电流谐波进行检测，要注意开关频率的设置，检测时必须进行相应的滤波。

【参考文献】

[1]钱雅云，马宏忠.双馈异步电机故障诊断方法综述[J].大电机技术，2011(5)： 5-8.

[2]李爽.双馈式风力发电机转子绕组匝间短路故障研究[D].保定： 华北电力大学，2012.

[3]刘竞.变速恒频风力发电系统的建模与仿真研究[D].广州： 华南理工大学，2010.

[4]黄守道，邓建国，罗德荣.电机瞬态过程分析的MATLAB建模与仿真[M].北京： 电子工业出版社，2013.

[5]马宏忠，胡虔生，黄允凯，等.感应电机转子绕组故障仿真与实验研究[J].中国电机工程学报，2003，23(4)： 107-112.

[6]GANDHI A， CORRIGAN T， PARSA L. Recent advance in modeling and online detection of stator inter-turn faults in electrical motors[J].IEEE Trans on industrial electronics，2011，58(5)： 1564-1575.

[7]马宏忠，时维俊，韩敬东，等.计及转子变换器控制策略的双馈风力发电机转子绕组故障诊断[J].中国电机工程学报，2013，33(18)： 119-125.

[8]张正东，马宏忠，陈涛涛.双馈异步发电机转子绕组不对称故障的诊断研究[J].微电机，2014，47(9)： 42-45.

[9]陈继宁，马宏忠，时维俊，等.基于希尔伯特-黄变换的双馈异步发电机定子故障诊断研究[J].大电机技术，2013(2)： 34-38.

[10]李俊卿，何龙，王栋.双馈式感应发电机转子匝间短路的负序分量分析[J].大电机技术，2014(2)： 14-18.

[11]李俊卿，王栋.双馈感应发电机转子匝间短路时定子电流谐波分析[J].电力系统自动化，2014，38(21)： 71-75.

[12]高景德，王祥珩，李发海.交流电机及其系统的分析[M].北京： 清华大学出版社，2005.

[13]张兴，张崇巍.PWM整流器及其控制[M].北京： 机械工业出版社，2012.

[14]STEFANI A，YAZIDI A，ROSSI C，et al.Double fed induction machines diagnosis based on signature analysis of rotor modulating signals[J].IEEE Transactions on Industrial Application，2008，44(6)： 1711-1721.