高速静压内置式电主轴系统稳定性分析及优化
第一作者郭维祺男,硕士生,1988年生
通信作者刘桂萍女,硕士生导师,1980年生
高速静压内置式电主轴系统稳定性分析及优化
郭维祺,刘桂萍,毛文贵
(湖南大学汽车车身先进设计制造国家重点实验室,长沙410082)
摘要:针对高效精密机床电主轴系统的高速化,讨论液体静压主轴系统失稳机理,并对高速静压内置式电主轴系统进行稳定性分析;提出基于遗传算法的电主轴系统稳定性优化方法。以系统稳定性评价指标为优化目标、电主轴系统轴向尺寸参数为设计变量,采用高效微型遗传算法实现电主轴系统稳定性优化。该方法既能高效解决增强轴系稳定性优化问题,又可避免复杂结构参数修改;通过某高速磨床静压内置式电主轴系统稳定性分析及优化对该方法进行验证。结果表明,稳定性分析及优化后系统稳定性得到明显提高。
关键词:静压内置式电主轴系统;稳定性分析;优化;微型遗传算法
收稿日期:2013-11-08修改稿收到日期:2014-03-19
中图分类号:TH133.2文献标志码:A
Stability analysis and optimization for a high-speed built-in motorized hydrostatic spindle system
GUOWei-qi,LIUGui-ping,MAOWen-gui(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082,China)
Abstract:Aiming at the high speed trend of high precision machine tool spindle systems, to study their stability in design process becomes very important. Firstly, the instability mechanism of a hydrostatic spindle system was discussed and the stability of a high-speed built-in motorized hydrostatic spindle system was analyzed. Then, an optimization method named the mirco genetic algorithm for stability of a motorized spindle system was proposed based on the genetic algorithm. The objective was to maximize the stability evaluation index of the system and the axial size parameters of the spindle system were taken as the design variables. The effective micro genetic algorithm was adopted for the stability optimization of the spindle system. Eventually, higher stability was achieved, the modification of the parameters of complex structure was avoided. As an example, the stability of a high-speed grinder motorized hydrostatic spindle system was analyzed and then optimized using this optimization method. The results indicated that the stability of the motorized spindle system can be improved obviously with the proposed method.
Key words:built-in motorized hydrostatic spindle system; stability analysis; optimization; micro genetic algorithm
电主轴具有调速范围宽、转动惯量小、响应快、易于实现精密控制等优点,而将液体静压轴承与内置式电主轴系统结合的新型主轴结构具有承载能力大、振动小、寿命长等优点成为机床主轴领域新的研究热点。由于高速化,超临界运转主轴系统的稳定性尤其重要。其中液体静压轴承作为系统的重要组成部分,既是阻尼源也是失稳源[1],对主轴系统稳定性影响较大。因此须对静压电主轴系统高速的稳定性进行分析及优化。
对油润滑静压轴承主轴系统,其油膜涡动、振荡为主轴在动态油膜力作用下发生的自激振动[2],亦是常见的轴系失稳现象。影响动态油膜力的主要因素是静压轴承的动力特性及主轴转速,对静压主轴系统稳定性分析、优化多由主轴的工作转速及静压轴承动力特性入手,如Mane等[3]研究转速与主轴稳定性关系; Bediaga等[4]提出主轴转速自动调节策略以保证系统最佳稳定性;朱均等[5]用广义阻尼建立系统稳定裕度准则,并研究单个轴承对系统稳定性裕度影响;周军波等[6]以提高轴系稳定性裕度为目标,以滑动轴承宽径比及相对间隙为优化变量,对滑动轴承进行优化设计。对静压电主轴系统,往往通过选择合适的电机转速、采取某种转速控制策略保证系统稳定运行,而通过静压轴承结构优化设计改进轴承动力特性、提高稳定性理论上可行,但由于液体静压轴承本身结构复杂、可调整范围窄、精度要求高,故对实际的主轴系统操作难度大、成本较高。顾卫东等[7]研究多跨转子系统轴承标高对滑动轴承稳定性影响表明,可通过调整轴荷分配提高轴系稳定性。即通过修改轴系轴向尺寸调整轴系质量分布从而改变前后轴承载荷分配,而静压轴承动力特性系数亦随载荷改变。既可提高轴系稳定性,又避免轴承结构改动,易于操作,成本低廉。
本文讨论液体静压主轴系统油膜失稳机理,针对高速静压内置式电主轴系统构建有限元模型,进行稳定性分析,并在考虑通过优化轴荷分配提高稳定性基础上,提出基于遗传算法的稳定性优化方法,即以系统稳定性裕度为优化目标,选取与轴荷分配有关系统参数为优化变量,采用性能优良的微型遗传算法,并用典型的工程实例对该方法进行验证。
1高速静压内置式电主轴系统稳定性分析
1.1高速静压内置式电主轴系统结构
高速内置式电主轴系统采用变频电动机与主轴合二为一的结构形式,即将带冷却套的电动机定子装配在主轴单元壳体内,主轴单元壳体即为电动机座,电动机空心转子与机床主轴旋转部件直接过盈热装成一体,作为内置式集成电动机主轴。主轴与高速电机转子在电磁转矩驱动下同轴旋转,实现电动机与主轴间 “零传动”的机电能量转换[8]。高速静压内置式电主轴采用液体静压轴承作为高速电主轴支撑,通过一套独立的供油系统形成全流体膜承载,结构示意图见图1。
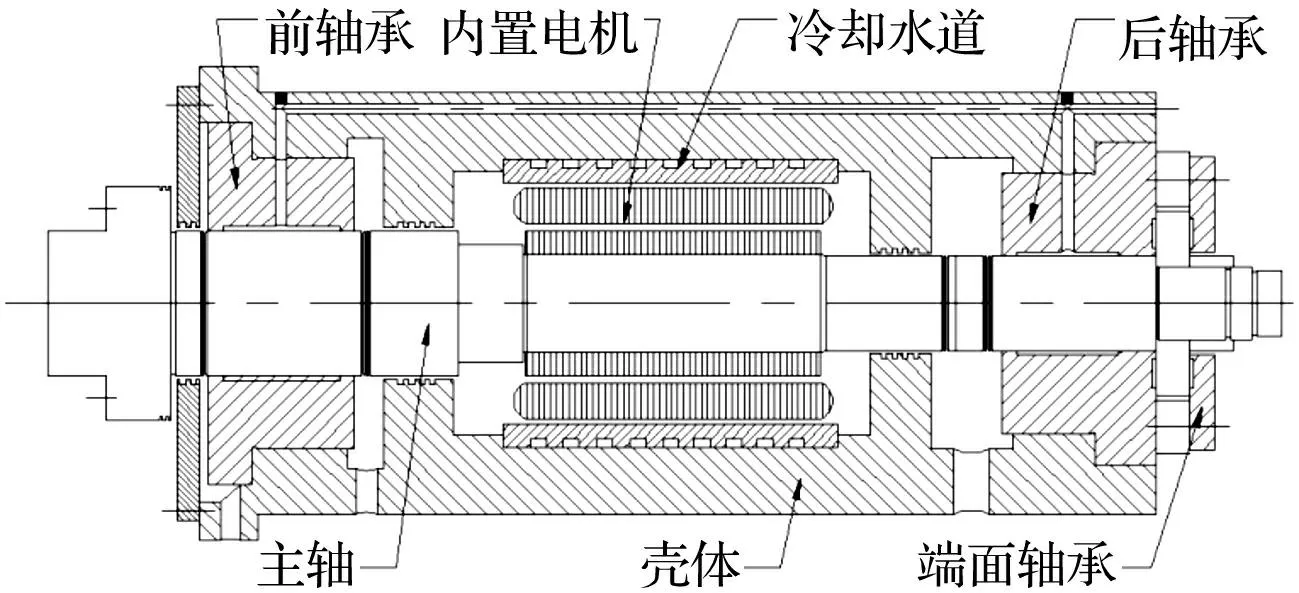
图1 高速静压内置式电主轴结构示意图 Fig.1Structure schematic of high-speed built-in motorized hydrostatic spindle
1.2静压电主轴系统稳定性分析
静压轴承中润滑油周向流动产生作用于轴颈的动态油膜力为主轴系统失稳主要因素。静压轴承油膜力用8个轴承动特性系数[9]表示,即4个刚度系数kxx、kxy、kyx、kyy,4个阻尼系数cxx、cxy、cyx、cyy。轴承油膜4个刚度力及4个阻尼力对系统做功,有的做正功,有的做负功,当正功大于负功时轴心轨迹发散,系统失稳,反之轨迹收敛,系统稳定。一般固定瓦静压轴承中交叉刚度力做正功,促使涡动产生;而阻尼系数为正时阻尼力做负功,反之阻尼力做正功。轴承以外阻尼作用不计时,系统稳定性取决于油膜力总的做功情况。由于静压轴承本身存在交叉刚度系数及负阻尼系数总会激发系统不稳定,故静压轴承刚度阻尼系数是影响轴系稳定性的重要参数。
然而单用静压轴承8个系数并不能判断系统稳定与否。据系统绝对稳定性特征值判据,系统所有特征值实部均小于零时认为系统稳定;至少有一个特征值实部大于零时认为系统不稳定。由于超临界转速运行与机电耦合影响,电主轴系统在启动、升速及载荷突变过程中往往表现出非平稳性。因此对高速电主轴系统仅保证工作转速在稳定区域是不够的,为提高系统的可靠性,须保证轴系具有足够的稳定性裕度以抵抗各种外界干扰。系统稳定性裕度的度量指标包括系统对数衰减率、系统阻尼等。
计算系统稳定性裕度应先求解系统的复特征值。即求解系统自由振动运动方程特征值
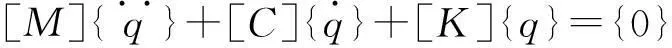
(1)
式中:[M]为系统质量矩阵,由主轴及与其固连的旋转部件质量构成;[C]为系统阻尼矩阵,本文仅考虑轴承提供的集中阻尼;[K]为系统质量矩阵,由转轴刚度系数构成的矩阵与液体静压轴承刚度系数构成的矩阵组成;{q}为位移矢量。
由于考虑陀螺效应、液体静压轴承阻尼力及弹性力耦合性质,对式(1)的特征值求解,不能作为小阻尼系统处理,且[K]并非对称矩阵,因此在结构动力学中求解特征值问题的某些方法并不适用。对此类转子动力学特征值问题,一般化为标准特征值问题后采用QR算法求解[10]。
式(1)中[K],[C]即包括静压轴承的4个刚度、阻尼系数,通过非定常运动雷诺方程可对其求解,而对常用的滑动轴承形式,亦可通过查表插值获得轴承8个动特性系数。求得系统复特征值即可得到各阶特征值的实部与虚部,进一步求得轴系稳定性裕度。以轴系对数衰减率为例,设第j阶复特征值实部为Re(υ)j,虚部为Im(υ)j,其第j阶对数衰减率[11]为
δj=-2πRe(υ)j/Im(υ)j
(2)
以其中最小值作为系统的对数衰减率,即δ=min(δj),用以表征系统的稳定性裕度。
对结构确定的主轴系统,各阶对数衰减率因随电主轴转速变化增加或减小,影响系统稳定性。当某阶对数衰减率下降为0时系统失稳,此时主轴转速称系统失稳转速。对电主轴稳定性分析应计算不同转速下主轴系统稳定性裕度变化。图2为某电主轴系统对数衰减率随主轴转速变化关系。由图2可知,系统对数衰减率随主轴转速上升而减小,当主轴转速达7 500 r/min时,系统对数衰减率δ<0,系统已失稳。

图2 某电主轴系统对数衰减率随转速变化关系 Fig.2 The log decrement changes with the rotation speed of a motorized spindle system
2高速静压内置式电主轴系统稳定性优化
2.1优化问题描述
主轴系统结构优化问题可描述为
maxf=(x1,x2,…,xn)
s.t.gi(x1,x2,…,xn)≤0,(i=1,…,p)
hj(x1,x2,…,xn)=0,(j=1,…,q)
(x1,x2,…,xn)∈X
式中:f为优化目标,即使系统稳定性裕度最大,系统稳定性裕度量化指标一般可取对数衰减率、阻尼或减稳因素界限值等;gi(i=1,…,p),hj(j=1,…,q)分别为不等式及等式约束函数;xj(j=1,2,…,n)为优化变量,即待优化的轴系结构参数,本文中优化变量避开结构复杂部件如液体静压轴承的结构参数,选择精度要求相对较低、易于修改的轴系轴向尺寸参数等。在模型基本结构确定后可初步选择主轴转速及影响轴荷分配的轴向尺寸参数,如轴承跨距、内置电机位置、加工端悬置量等,再通过敏感性分析选择对目标函数影响较大参数;X为优化变量搜索区间,据机床整体结构设计及各部分间协调关系确定。
2.2微型遗传算法
遗传算法[12]为模拟自然界生物遗传进化过程形成的全局优化概率搜索法。运算中以多个个体组成的种群为对象,经反复迭代过程不断对个体施加遗传、进化操作,最终所留即为适应度最高的个体。
对电主轴系统稳定性优化问题,稳定性裕度与轴系结构参数间映射关系无法用显式函数表达,需通过复杂计算模型表示,致求解难度加大。遗传算法由于具有基于种群运算的基本特征及可在不考虑问题具体特征前提下用于解搜寻的进化本质,因此非常适合该问题求解。
传统遗传算法种群规模大、收敛效率低。而微型遗传算法采用小规模种群,计算效率高且收敛速度快[13]。微型遗传算法种群因通常含5~8个个体,较易产生早熟收敛,因此为保证小规模种群基因多样性,避免早熟收敛,运算中加入重启动策略。一旦种群收敛,则在设计空间生成新种群,并仅保留原种群的最优个体,其余个体则在整个搜索空间内随机生成。
2.3基于微型遗传算法的电主轴系统稳定性优化过程
电主轴系统稳定性优化应先确定优化目标,一般取系统稳定性裕度的量化指标(含系统对数衰减率、系统阻尼或减稳因素界限值等)。优化变量选取应通过敏感性分析选对目标函数影响较大参数,约束条件及变量搜索区间则据实际情况而定。据以上步骤建立电主轴系统稳定性优化问题后进行基于有限元法建立电主轴系统稳定性分析计算模型,用微型遗传算法进行优化,达到收敛条件后输出优化结果。电主轴系统稳定性优化过程见图3。
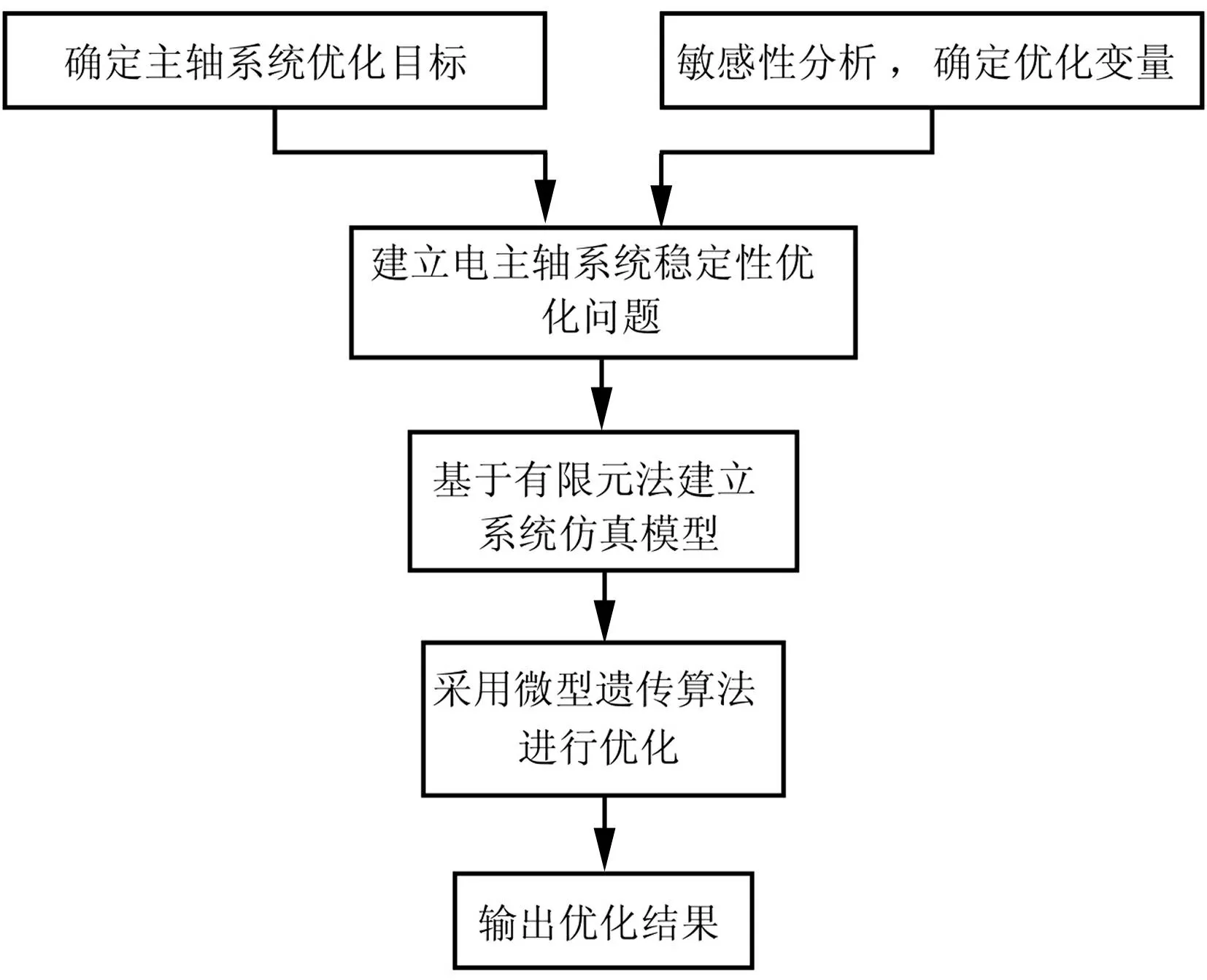
图3 电主轴系统稳定性优化流程图 Fig.3 Flow chart of the optimization process
3工程实例
以某高速磨床静压内置式电主轴系统为例验证本文方法。初始设计电主轴系统额定转速为6 000 r/min,前后径向轴承采用圆柱形液体静压轴承。
3.1初始设计电主轴系统稳定性分析
该高速磨床静压内置式电主轴系统简化示意图见图4。

图4 高速磨床静压内置式电主轴系统简化示意图 Fig.4 Schematic of motorized hydrostatic spindle system of high-speed grinding machine
建立系统有限元仿真模型进行稳定性分析。由于所有旋转部件均为回转体,故采用管单元PIPE16模拟旋转部件,并考虑系统陀螺效应;静压轴承采用COMBI214单元模拟,该单元8个实常数分别代表静压轴承4个刚度系数(单位N/m)及4个阻尼系数(单位N·s/m)。圆柱形液体静压轴承的8个系数由查表插值获得,即
前轴承为
后轴承为
通过仿真分析获得该高速磨床静压内置式电主轴系统对数衰减率随转速变化关系见图5。由图5可知,系统对数衰减率随主轴转速上升而减小。当主轴系统以额定转速6 000 r/min运行时,系统对数衰减率δ=0.243 3,而δ<0.25被认为处于失稳边缘。由此可判断该电主轴系统稳定性裕度偏低,其初始设计参数不合理,应进行优化以提高系统稳定性裕度。

图5 高速磨床静压内置式电主轴 对数衰减率随转速变化关系 Fig.5 The log decrement changes with the rotation speed of motorized hydrostatic spindle system of high-speed grinding machine
3.2电主轴系统稳定性优化问题建立
初步选择与主轴跨距、电机位置、加工端悬置量等相关的轴向尺寸L1、L2、L3、L4及主轴转速为设计变量,见图6。图中,L1为后轴承中心至轴端距离;L2为电机转子重心至后轴承中心距离;L3为电机转子重心至前轴承中心距离,L2+L3为主轴跨距;L4为砂轮中心至前轴承中心距离,即加工端悬置量。
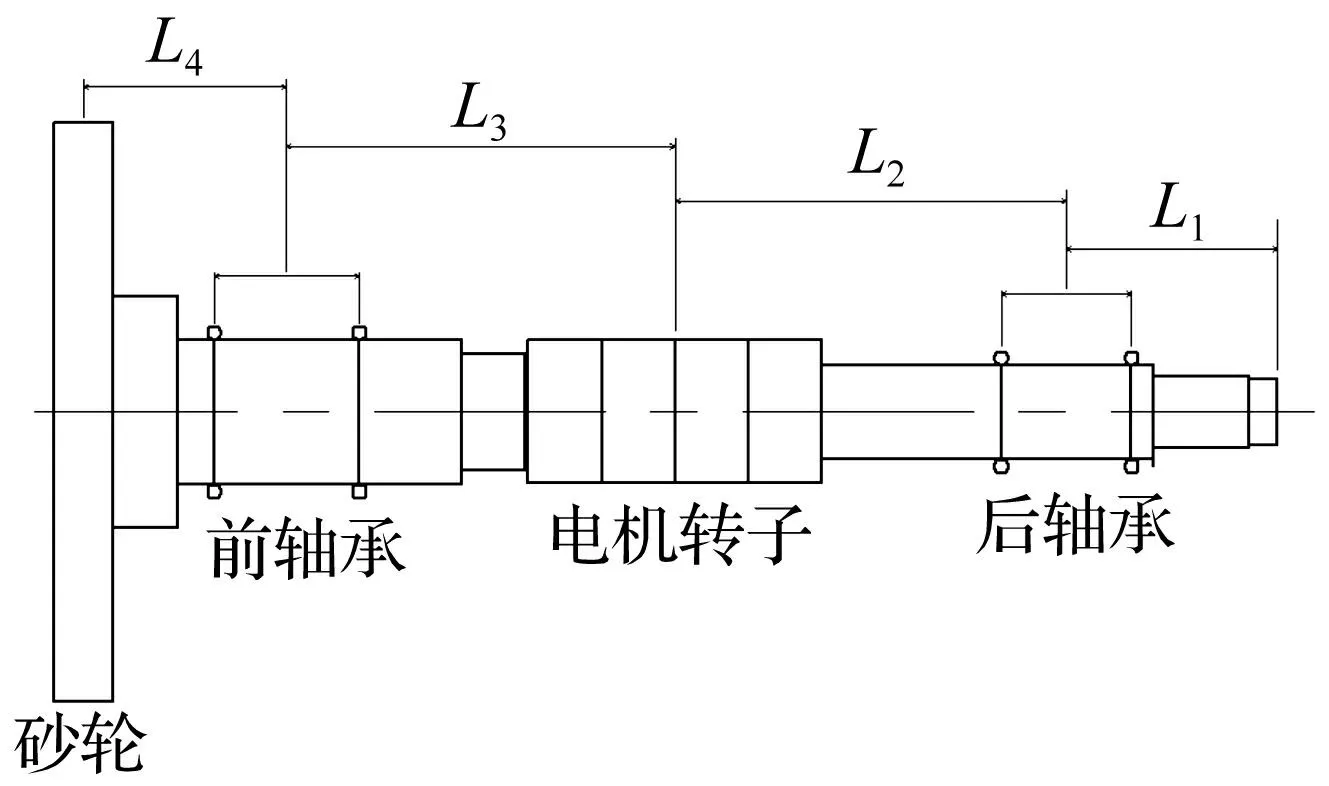
图6 优化变量示意图 Fig.6 Schematic of the design variables
以提高系统对数衰减率为目标,分别变化L1、L2、L3、L4时系统对数衰减率变化趋势见图7。由图7可知,仅L1与系统对数衰减率变化趋势是单调的,且系统对4个结构参数均较敏感,而由稳定性分析知系统稳定性裕度对主轴转速亦较敏感。
该主轴系统稳定性优化问题可描述为
maxf=(L1,L2,L3,L4,n)=δ
s.t.0.104 m≤L1≤0.184 m
0.230 m≤L2≤0.320 m
0.226 m≤L3≤0.316 m
0.105 m≤L4≤0.165 m
3 000 r/min≤n≤10 000 r/min
式中:δ为系统对数衰减率,以最大化为优;L1,L2,L3,L4为结构参数(单位m);n为主轴转速(单位r/min);各优化变量搜索区间据结构而定。
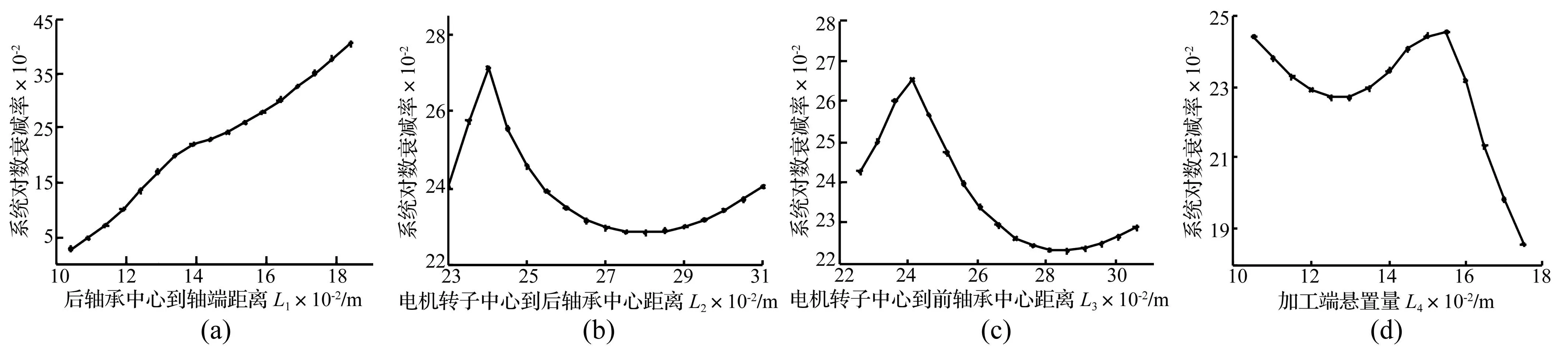
图7 轴系对数衰减率随优化变量变化趋势 Fig.7 The log decrement changes with the design variables of motorized hydrostatic spindle system
3.3优化结果及分析
微型遗传算法所用参数为:种群大小取5,交叉概率取0.9,变异概率取0.02。进化计算825次后输出优化结果。优化前后对比见表1。由表1看出,通过优化系统对数衰减率达到0.545 1,较优化前提高124%,达到对数衰减率δ≥0.5[8]推荐值。计算优化后的主轴系统第二阶临界转速低于1 000 r/min,第三阶临界转速为15 176 r/min,故主轴系统工作转速处于第二、三阶临界转速之间,已远离共振区域。
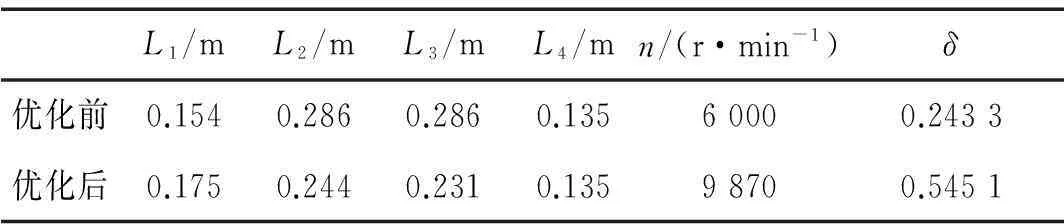
表1 优化前后参数对比
静压轴承刚度阻尼系数优化前后对比见表2。由表2看出,优化后的轴承刚度阻尼系数均有不同程度减小,而系统稳定性反而有较大幅度提高,说明轴承刚度阻尼并非越高越好。表2中该主轴系统静压轴承阻尼系数无负数项,其阻尼力总做负功,抑制系统失稳;而交叉刚度总做正功,促发失稳。刚度力与阻尼力对系统稳定性贡献相反,其数值大小改变对系统稳定性影不能直观体现。而上述方法避开了复杂轴承参数修改,对次要参数进行优化,通过微型遗传算法提高系统稳定性,足以表明本文方法的有效性。

表2 优化前后轴承系数对比
4结论
(1)本文通过讨论液体静压主轴系统油膜失稳机理,建立高速静压内置式电主轴系统模型,进行系统稳定性分析,提出基于遗传算法的电主轴系统多参数优化方法。以提高系统稳定性裕度为优化目标,通过敏感性分析选取电主轴轴向尺寸参数为优化变量,采用高效微型遗传算法为优化算法实现电主轴系统稳定性的优化。
(2)该方法避开复杂轴承参数修改,采取对次要参数优化方式及微型遗传算法,高效解决电主轴系统稳定性优化问题。并通过对某高速磨床静压内置式电主轴系统稳定性分析、优化。结果表明,优化后该电主轴系统对数衰减率达0.5451,较优化前提高124%。表明用本文方法可使系统稳定性显著提高。
参考文献
[1]张卫,朱均.大型转子-滑动轴承系统运动稳定性的研究[J].西安交通大学学报,1995,29(8):66-71.
ZHANG Wei,ZHU Jun.The study of dynamic stability of the complex rotor bearing systems [J].Journal of Xi’an Jiaotong University,1995,29(8):66-71.
[2]闻邦椿,顾家柳,夏松波,等.高等转子动力学[M].北京:机械工业出版社,1999.
[3]Mane I,Gagnol V,Bouzgarrou B C,et al.Stability-based spindle speed control during flexible workpiece high-speed milling[J].International Journal of Machine Tools & Manufacture,2008(48):184-194.
[4]Bediaga I,Munoa J,Hernandez J,et al.An automatic spindle speed selection strategy to obtain stability in high-speed milling[J].International Journal of Machine Tools & Manufacture,2009(49):384-394.
[5]袁小阳,朱均.大型汽轮发电机轴系稳定裕度研究[J].西安交通大学学报,1994,28(9):52-57.
YUAN Xiao-yang,ZHU Jun.Degree of stability of large turbine-generator rotors[J].Journal of Xi’an Jiaotong University,1994,28(9):52-57.
[6]周军波,丁毓峰.基于轴系稳定性分析的滑动轴承优化设计[J].机械制造,2010,552(48):41-44.
ZHOU Jun-bo,DING Yu-feng.Optimization design of sliding bearing based on stability analysis of spindle system [J].Journal of Machinery,2010,552(48):41-44.
[7]顾卫东,王永亮,方勃,等.标高对转子-滑动轴承系统动力学特性影响研究[J].汽轮机技术,2011,53(2):125-128.
GU Wei-dong,WANG Yong-liang,FANG Bo,et al.Research on characteristics of rotor-bearing system with different bearing elevation[J].Journal of Turbine Technology, 2011, 53(2):125-128.
[8]单文桃,陈小安,合烨.不同控制策略对高速电主轴动态性能影响[J].振动与冲击,2013,32(18):75-80.
SHAN Wen-tao,CHEN Xiao-an,HE Ye.Effects of different control strategies on dynamic performance of a high-speed motorized spindle[J].Journal of Vibration and Shock, 2013, 32(18):75-80.
[9]许尚贤.液体静压和动静压滑动轴承设计[M] .南京:东南大学出版社,1984.
[10]钟一谔,何衍宗,王正,等.转子动力学[M] .北京:清华大学出版社,1987.
[11]徐龙祥.高速旋转机械轴系动力学设计[M].北京: 国防工业出版社,1993.
[12]周明,孙树栋.遗传算法原理及应用[M] .北京:国防工业出版社,1999.
[13]Liu Gui-rong,Han Xu.Computational inverse techniques in nondestructive evaluation[M].Florida: CRC Press, 2003.


