磁悬浮主被动隔振系统自适应控制及非线性补偿
第一作者李彦女,博士,讲师,1984年6月生
磁悬浮主被动隔振系统自适应控制及非线性补偿
李彦,何琳,帅长庚,吕志强
(海军工程大学振动与噪声研究所船舶振动噪声重点实验室,武汉430033)
摘要:针对船舶机械设备低频线谱隔振,提出采用磁悬浮作动器的主被动隔振系统,研究自适应振动控制方法。对磁悬浮作动器用于主被动隔振时的非线性效应进行分析,并采用理论建模及测试修正相结合方式,建立作动器的非线性逆模型,提出具有非线性逆模型补偿环节、分频段控制的改进FxLMS算法,运算量小、实时性好。多通道磁悬浮主被动隔振装置实验结果表明,该自适应算法能显著减小低频线谱振动能量,可有效抑制作动器非线性引起的振动。
关键词:主被动隔振;磁悬浮作动器;非线性逆模型;自适应控制
收稿日期:2013-07-24修改稿收到日期:2014-02-25
中图分类号:Tp12;Tp13.3文献标志码:A
基金项目:国家重点基础研究发展计划(“973”计划)项目(2012CB026000)国家自然科学基金重点项目(51135001)
Adaptive control and nonlinear compensation for a passive-active hybrid vibration isolation mount using maglev actuator
LIYan,HELin,SHUAIChang-geng,LÜZhi-qiang(Institute of Noise & Vibration, Naval University of Engineering National Key Laboratory on Ship Vibration & Noise, Wuhan 430033,China)
Abstract:In order to effectively control the low frequency vibration of ship machineries, a passive-active hybrid vibration isolation mount using maglev actuator was proposed. Maglev actuator with non-contact structure, low stiffness and rapid response is excellent for active vibration isolation. However, the actuator’s nonlinearity has to be restrained with a control algorithm. The nonlinearity of a maglev actuator was analyzed, its nonlinear reverse model was built using theoretical analysis and experimental correction, and an improved FxLMS algorithm based on reverse model linearization and frequency range division control was put forward. It had the advantage of low computation cost for the real time control. Tests were performed on a multi-DOF passive-active vibration isolation system. The results showed that the improved FxLMS algorithm can effectively be used to reduce the vibration energy at targeted frequency, and suppress the nonlinearity-induced vibration of the actuator.
Key words:passive-active vibration isolation; maglev actuator; nonlinear reverse model; adaptive control
机械振动线谱是舰船的“指纹特征”,声纳及声制导水中武器对水声中低频线谱噪声的探测能力越来越强。被动隔振技术虽经数十年发展已达到近40 dB的隔振效果[1],但无法有针对性消除低频线谱特征。主动隔振技术因能有效控制低频线谱振动引起广泛关注,并取得大量理论和实验研究成果。六自由度Stewart平台为航天工程常用的主动隔振装置[2],其作动器通常为电磁式或磁致伸缩式。NEWPORT公司的Elite-3精密主动隔振平台利用压电作动器对地板的低频振动进行隔离[3]。由于作动器具有一定局限性,为接触式,需承载设备重量,且刚度较大,主要用于航空航天领域及光学精密仪器等轻载设备隔振,难以用于重量大、振动剧烈、相对位移较大的舰船动力机械。而磁流变或电流变作动器响应速度相对较慢,不太适用振动主动控制。
磁悬浮作动器具有无接触、负刚度特点,可与被动隔振器并联构成主被动混合隔振系统,由被动隔振器承载设备重量并隔离宽频振动,对作动器进行主动控制从而衰减线谱振动。在磁悬浮主被动隔振系统中,作动器无需承受设备重量,只需控制宽频隔振后残余线谱振动,具有低功耗、高可靠优点,适用于舰船机械设备隔振,对提高舰船水声隐蔽性具有重要意义。
磁悬浮作动器为高效、响应迅速的优良作动器,但输入电流与输出力间存在非线性,因此需通过控制算法进行补偿。Snyder等[4-7]研究的主动隔振/消声系统非线性控制,大部分算法需建立非线性次级通道模型,且含大量参数,辨识、控制时运算量较大,难以实时应用。安峰岩等[8-9]提出基于径向基函数网络的自适应控制算法,采用线性次级通道模型对误差信号进行滤波,但该模型须为物理系统的高阶次时域模型,难以用于冲击响应时间较长的隔振系统实时控制。
本文分析磁悬浮作动器用于主被动隔振的非线性效应,并据作动器性能测试数据建立非线性逆模型,提出具有非线性逆模型补偿环节、分频段控制的改进FxLMS算法。该算法通过逆模型预失真环节将控制系统次级通道线性化,采用较低阶控制滤波器及次级通道模型,运算量小、实时性好。多自由度主被动隔振系统实验表明,该算法可显著衰减低频线谱振动,并能对作动器非线性有效补偿,振动控制效果良好。
1磁悬浮隔振系统自适应控制
磁悬浮主被动隔振系统将磁悬浮作动器与被动隔振器并联安装于设备、基座之间。设备运转时产生振动激励,被动隔振器使振动传递得到衰减,而磁悬浮作动器输出控制力,抵消传递到基座的低频线谱振动,系统见图1。
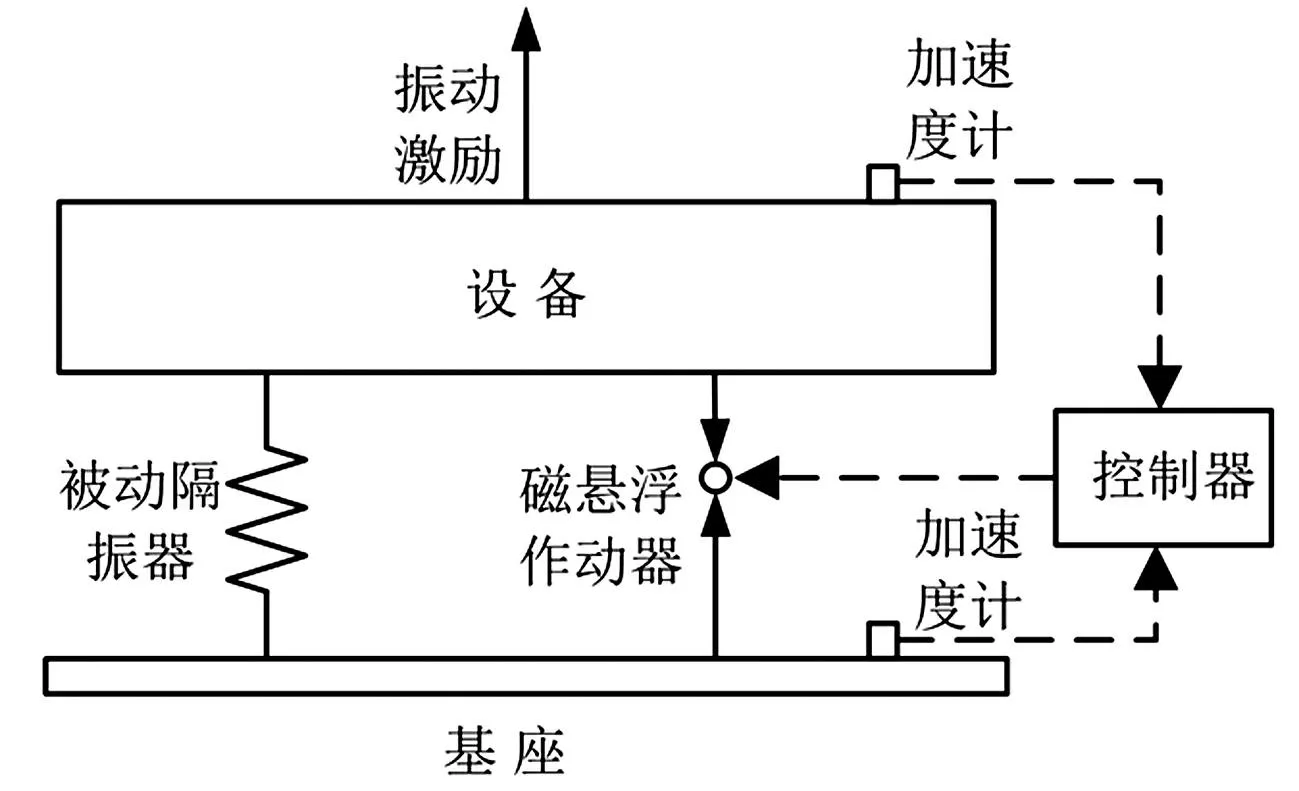
图1 磁悬浮主被动隔振系统模型 Fig.1 Passive-active hybrid isolation system using maglev actuator
自适应控制可跟踪系统状态变化,使控制效果始终维持在最优值附近;算法对模型精确度要求较低,且多数情况下收敛后的控制效果与模型误差无关[10]。基于该优点,采用自适应方法对低频线谱振动进行控制。滤波参考信号最小均方算法(Filtered-x Least Mean Square,FxLMS)为考虑次级通道(控制信号输出与误差信号测点间环节)影响的求最优化控制器权值的递推方法。
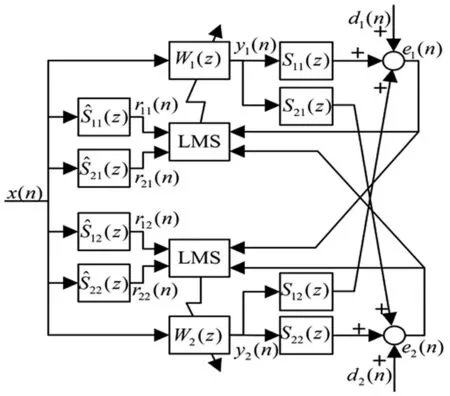
图2 多通道FxLMS算法框图 Fig.2 Diagram of multi-channel FxLMS algorithm

设第l个控制滤波器系数为wli(i=0…N),第l路控制信号至第k路误差信号间冲击响应为hklj(j=0…M),则有
(1)
(2)
代价函数为
(3)
相对控制滤波器系数梯度为
(4)
据梯度下降法原理,控制器更新公式为
(5)
(6)

对线性系统主动控制,FxLMS算法可取得较好的控制效果。而磁悬浮作动器输入电流与输出力间存在非线性,因此需研究能补偿作动器非线性的改进FxLMS算法。
2具有非线性补偿环节的自适应控制
2.1磁悬浮作动器机电耦合模型
系统所用永磁偏置型磁悬浮作动器见图3。作动器铁芯端面装有永磁体形成偏置磁场,产生偏置吸引力。为线圈输入控制电流产生的磁场与偏置磁场方向相同时吸引力增大;与偏置磁场方向相反时吸引力减小。因此给线圈输入交变电流可获得交变磁悬浮力。永磁偏置较电流偏置相比功耗、发热量小。

图3 磁悬浮作动器原理结构图 Fig.3 Diagram of maglev actuator

图4 U型结构作动器磁路网络 Fig.4 Magnetic circuit of U-structure actuator
设永磁体高度hm,气隙z,外侧磁极宽度a1,中间磁极半宽a2,铁芯厚度b,线圈匝数N,电流i。将磁悬浮作动器从E型铁芯中间平分,忽略漏磁、铁芯及衔铁磁阻,由磁路欧姆定律建立其半边U型结构的等效磁路网络,见图4。其中Fm1,Fm2为左右永磁体等效磁势;Rm1,Rm2为永磁体等效磁阻;Rz1,Rz2为左右气隙磁阻。
设永磁体材料的矫顽力为Hc,剩磁为Br,空气磁导率为μ0,则磁势、磁阻计算式为
Fm1=Fm2=Hchm
(7)
(8)
(9)
据磁路欧姆定律及磁通连续性原理,气隙中磁通量为
(10)
设左右气隙处磁感应强度为B1、B2,则有
Φ1=Φ2=B1a1b=B2a2b
(11)
铁芯对衔铁的力与正对面积及气隙处磁感应强度的平方成正比。U型作动器永磁力与电磁力合力FU为
(12)
E型作动器合力FE为
(13)
综合式(7)~式(13),有
(14)
得E型作动器电磁力Fg为
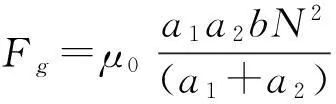
(15)
由式(15)知,作动器的电磁力Fg取决于输入电流i及气隙z两变量,与两者均有非线性关系,但只有电流i为控制量,本文将磁悬浮作动器用于约20~100 Hz 频段主被动隔振,作动器气隙波动较小(如20 Hz,上层振级120 dB时,<0.1 mm),而额定气隙为5 mm,气隙可认为固定值。式(15)可写为
(16)

永磁体偏置B0应设计得足够大,以确保在作动器额定工作电流范围内电磁力Fg是电流i的单调函数。
2.2控制线谱振动的非线性现象
设作动器同时控制双频线谱振动,输入交变电流为
i=A1cos(ω1t)+A2cos(ω2t)
(17)
电磁力Fg为
(18)
由式(18)知,进行振动主动控制时,若磁悬浮作动器非线性得不到补偿,则其输出力除基波外亦含二倍频、和频、差频成分及微小偏置。因此,应对磁悬浮作动器非线性进行补偿,避免主动隔振时产生额外频率振动。
2.3具有逆模型非线性补偿环节的自适应控制
逆模型补偿原理即建立作动器电磁力的逆模型解析式用于补偿,将系统次级通道线性化,从而可采用线性控制器进行主动控制。


图5 具有逆模型非线性 补偿环节的FxLMS控制原理图 Fig.5 Principle for FxLMS algorithm with nonlinear compensation based on reverse model
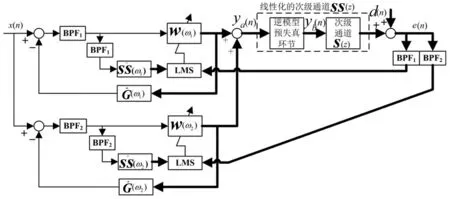
图6 具有非线性补偿环节的分频段FxLMS控制 Fig.6 Principle for frequency range division control with nonlinear compensation

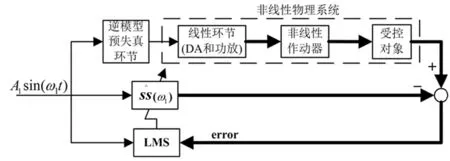
图7 次级通道模型辨识原理图 Fig.7 Principle of secondary path identification
2.4作动器测试及逆模型建立
通过作动器测试对理论模型进行修正,弥补忽略漏磁及边缘效应影响,使电磁力模型更准确。作动器特性测试装置见图8,在额定气隙5 mm时输入不同频率、幅值的交变电流测量作动器线圈电流及电磁力。

图8 磁悬浮作动器性能测试装置 Fig.8 Characteristic test device for Maglev actuator
模型计算及测试结果见图9、图10。由二图看出,电流较小时作动器输出力近似线性,力的二次谐波与基波能量落差在-35 dB以上;输入电流较大时力的非线性随之增大,落差约-17 dB。在各频率工况下上述特性具有一致性。作动力与电流基波相位差见图11。由图11看出,在10~110 Hz频段,作动器力与电流基波相位差<5o。实验结果表明,磁悬浮作动器的非线性主要含输入电流的平方项,磁滞现象所致相位滞后较小,可将作动器视为具有瞬时输入输出关系的无记忆系统,故式(16)模型无需相位滞后修正。将磁悬浮作动器尺寸、线圈匝数、材料特性等参数代入式(16)可得磁悬浮力的理论计算模型为
(19)
由图9、图10知,磁悬浮力的实测值小于理论模型计算值,且二次谐波与基波能量落差的实测值与计算值有差异。此为气隙处存在漏磁及边缘效应所致。


图9 作动器电磁力模型计算及测试结果Fig.9Calculatedandexperimentalresultsofelectromagneticforce图10 电磁力非线性度模型计算及测试结果Fig.10Calculatedandexperimentalresultsofelectromagneticforce’snonlinearity图11 作动力与电流基波相位差Fig.11Fundamentalharmonicphaselagofforceandcurrent
利用图9、图10中测试数据拟合修正式(19)的分母及二次项系数,修正后模型为
(20)
由图9、图10知修正模型计算的磁悬浮力与实测结果吻合较好。
经DA及功率放大器后,电流i与控制信号yb的关系为i=10yb,即

(21)
作动器设计时使电磁力为电流的单调函数,则作动器电磁力的逆模型为
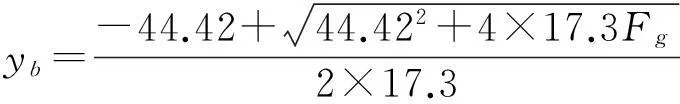
(22)
3非线性自适应控制实验研究
图12为多自由度主被动混合隔振实验系统,对其采用具有非线性补偿环节的多通道FxLMS算法进行主动振动控制实验,研究控制效果。上层质量、基座分别为500 kg及1000 kg,两者间由4个主被动混合隔振器连接。输出力1 000 N激振器安装在上层质量作为振源。控制器用TMS320c6713B-300芯片作为核心数字信号处理器,高速AD与DA精度均为16 bit,功率放大器可同时独立驱动多个作动器。振动控制系统目标为使传递到基座的振动得到衰减。

图12 主被动混合隔振实验系统 Fig.12 Experiment system for passive-active hybrid vibration isolation
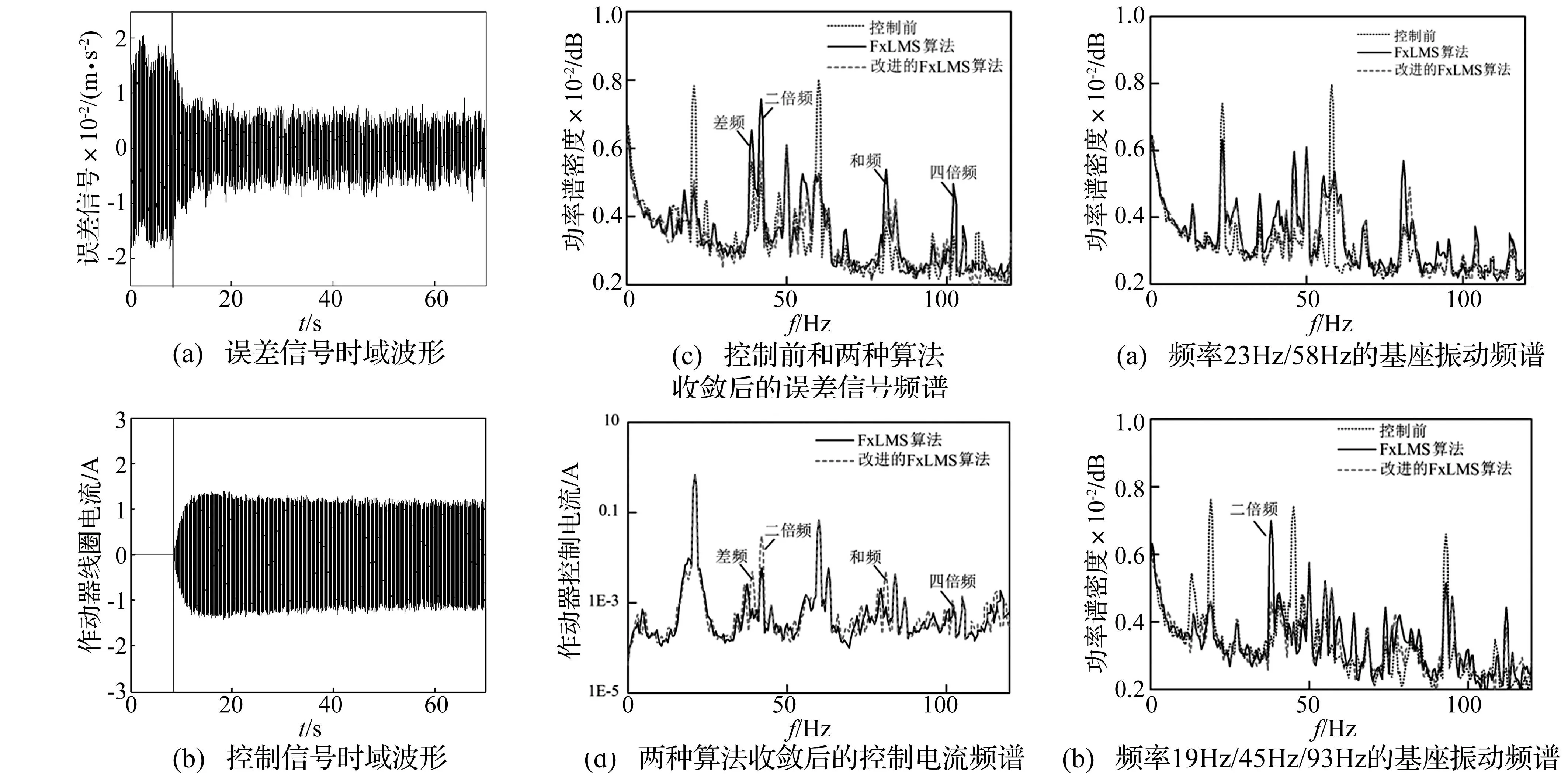

图13 频率21Hz/60Hz主动控制实验结果Fig.13Experimentalresults-activevibrationcontrolat21Hz/60Hz图14 其他频率的主动控制实验结果Fig.14Experimentalresults-activevibrationcontrolatotherfrequencies
任意选择19~100 Hz频段内不同频率组合多根线谱叠加白噪声作为振源信号。控制系统采样率1 000 Hz。主动控制器以上层质量加速度信号作为参考信号,以基座4个测点加速度信号作为误差信号。算法中各频带次级通道模型为15阶FIR滤波器,控制器为15阶。每个选频滤波器由2个4阶椭圆滤波器级联而成,每个滤波器阻带衰减为40 dB,通带波纹为2 dB。自适应控制过程收敛时,基座4个测点加速度均方和得到有效衰减,则可认为基座振动得到有效控制。
图13为激振频率21Hz+60Hz实验结果。由图13(a)、 (b)看出,第8 s时施加主动控制,10 s后基座的振动响应得到大幅抑制,控制电流相对稳定。由图13(d)看出,改进的FxLMS算法对控制电流进行预失真。图13(c)为采用普通与改进FxLMS算法控制后的基座振动功率谱对比,采用普通线性算法控制时基频21 Hz及60 Hz处振动分别衰减26 dB及24 dB,但谐频42 Hz、和频81 Hz、差频39 Hz处产生额外振动;而改进的FxLMS算法不仅使基频振动有效衰减,还较好抑制了非线性引起的谐频、和频、差频振动,使其明显降低至接近背景噪声。
为观察控制效果,在23 Hz+58 Hz及19 Hz+45 Hz+93 Hz频率组合下进行实验,见图14。由图14看出,改进的FxLMS算法基频控制效果分别为15 dB、26 dB与28 dB、30 dB、15 dB,且控制后无明显的非线性频率成分。
4结论
(1)针对具有非线性磁悬浮主被动隔振系统传统的线性控制算法效果不佳,而非线性控制算法运算量大、实用性不高,本文所提具有非线性逆模型补偿环节、分频段控制的改进FxLMS算法,将理论建模与实验修正相结合,建立磁悬浮作动器的非线性逆模型;使自适应控制器的输出信号通过逆模型补偿环节进行预失真处理,从而使次级通道线性化;将全频段划分为一定数量的窄带频段,各频段采用较低阶的控制滤波器及次级通道模型。
(2)本文算法在多通道磁悬浮主被动隔振实验装置上已有效实现多个频率组合的低频线谱振动自适应控制,每个频率谱峰衰减量达15~30 dB,且能较好抑制非线性引起的谐频、和频、差频振动。该算法具有收敛迅速、计算量小等优点,可为磁悬浮主被动隔振系统的工程实用奠定基础。
参考文献
[1]何琳,李彦,杨军. 磁悬浮-气囊主被动混合隔振装置理论和实验[J]. 声学学报,2013, 38(2): 241-249.
HE Lin, LI Yan, YANG Jun. Theory and experiment of passive-active hybrid vibration isolation mounts using electromagnetic actuator and air spring[J]. Acta Acustica, 2013, 38(2): 241-249.
[2]Thayer D, Campbell M, Vagners J, et al. Six-axis vibration isolation system using soft actuators and multiple sensors[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 206-212.
[3]Anderson E H, Houghton B. Elite-3 active vibration isolation workstation[J]. Proc. SPIE.,2001,4332: 183-196.
[4]Bouchard M. New recursive-least-squares algorithms for nonlinear active control of sound and vibration using neural networks[J]. IEEE Transactions on Neural Networks, 2001,12 (1): 135-147.
[5]Bambang R T, Yacoub R R, Uchida K. Identification of secondary path in ANC using diagonal recurrent neural networks with EKF algorithm[J]. Proceedings of the Fifth Asian Control Conference, Melbourne, Australia, 2004, 1: 665-673.
[6]Zhou D, DeBrunner V. Efficient adaptive nonlinear filters for nonlinear active noise control[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2007, 54 (3): 669-681.
[7]Napoli R, Piroddi L. Nonlinear active noise control with NARX models[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18 (2): 286-295.
[8]安峰岩,孙红灵,肖椽生,等. 基于磁悬浮作动器的自适应有源振动控制研究[J]. 声学学报,2010, 35(2): 146-153.
AN Feng-yan, SUN Hong-ling, XIAO Chuan-sheng, et al. Research on adaptive active vibration control using maglev actuator[J]. Acta Acustica, 2010, 35(2): 146-153.
[9]An Feng-yan, Sun Hong-ling, Li Xiao-dong. Adaptive active control of periodic vibration using maglev actuators[J]. Journal of Sound and Vibration, 2012, 331(9): 1971-1984.
[10]Elliott S J. Signal processing for active control[M]. London: Academic Press, 2001.
[11]Jeon H J,Chang T G, Yu S, et al. A narrowband active noise control system with frequency corrector[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(4): 990-1002.


