随机参数高速电梯轿厢系统共振可靠性灵敏度研究
第一作者张瑞军男,教授,1965年3月生
随机参数高速电梯轿厢系统共振可靠性灵敏度研究
张瑞军1,2,司鑫鑫1,杨围围1,董明晓1,2
(1.山东建筑大学,济南250101; 2. 山东建筑大学山东省高校机械工程创新技术重点实验室,济南250101)
摘要:针对高速电梯轿厢系统制造安装过程中误差使系统设计参数具有随机性问题,以实现轿厢系统共振可靠性灵敏度分析为目标,基于摄动技术导出轿厢系统固有频率与随机参数间关系式,分析参数随机性对固有频率影响;据振动稳定性准则构建基于激振频率变化的高速电梯轿厢系统共振失效功能函数,采用灵敏度技术导出轿厢系统共振可靠性灵敏度表达式,并进行灵敏度分析。结果表明,考虑参数随机性时轿厢系统固有频率存在分散性;取相同变异系数时导靴系统刚度及导轮安装位置对轿厢系统共振可靠性影响较大。该结果可为高速电梯轿厢系统防共振设计、安全评估提供参考。
关键词:高度电梯;轿厢系统;随机参数;共振;可靠性;灵敏度
收稿日期:2014-01-08修改稿收到日期:2014-03-27
中图分类号:TH113文献标志码:A
基金项目:教育部“新世纪优秀人才支持计划”资助;国防科技重点实验室
Resonance reliability sensitivity for a high-speeding elevator cabin system with random parameters
ZHANGRui-jun1,2,SIXin-xin1,YANGWei-wei1,DONGMing-xiao1,2(1.Shandong Jianzhu University, Jinan 250101,China;2. Key of Mechanical Engineering & Innovation Technology in Universities of Shandong,Shandong Jianzhu University, Jinan 250101, China)
Abstract:The errors in the process of manufacture and installation for a high-speed elevator cabin system made design parameters of the system posses randomness. To realize the analysis of resonance reliability sensitivity for the high-speed elevator cabin system, the relationship expressions between the natural frequencies of the system and the random parameters were derived with the perturbation technique to analyze the influence of the parametric randomness on the natural frequencies. According to the stability criterion of vibration for mechanical systems, the performance function of the resonance failure based on the variation of the exciting frequency for the system was built. Utilizing the sensitivity technique, the expressions of the resonance reliability sensitivity of the system were deduced to analyze the sensitivity. The results showed that the natural frequencies of the system have dispersibility considering the parametric randomness; the guide shoe stiffness and guide wheel mounting position have greater effects on the resonance reliability of the system with the same exciting frequency variation coefficient. The results provided a reference for anti-resonance design and safety assessment of high-speed elevator cabin systems.
Key words:high-speed elevator; cabin system; random parameters; resonance; reliability; sensitivity
随着现代城市中高层、超高层建筑物兴起,电梯亦向高速度方向发展。电梯轿厢系统高速运行时会产生剧烈振动影响其安全性,如何保证该系统振动时具有足够的可靠性颇受关注。近年来已有众多围绕电梯轿厢系统的深入研究[1-3]。梅德庆等[4]考虑滚动导靴的不圆度偏差及导轨廓形偏差,拟合出导靴-导轨不平顺激励的数学模型,并建立高速曳引电梯系统动力学方程。尹纪财等[5]考虑影响电梯水平振动的导轨不平顺度、弯曲及导靴自身缺陷等因素建立高速电梯轿厢多自由度水平振动模型。夏冰虎等[6]通过研究导轮、导轨间实时界面刚度变化建立轿厢水平振动模型。杜小强等[7]基于精细积分法对高速电梯工作行程内非线性水平振动响应进行仿真分析。然而,诸多文献均将电梯轿厢系统设计参数及作用激励载荷视为确定性参数,无法反映系统中随机因素对动力响应影响。实际上,电梯轿厢系统设计参数及作用载荷的随机性客观存在,且会引起轿厢系统振动特性的随机性。由于设计参数的随机性,使轿厢系统在规定条件及时间内不发生共振成为一种随机事件。因此,研究参数随机性对轿厢系统动力学行为影响及系统的共振可靠性灵敏度,对电梯轿厢系统减振及安全评估有重要意义。
翟红波等[8-9]分别采用点估计法及响应面法计算随机连续输流管道振动系统共振可靠度。张义民等[10-11]基于摄动理论分析随机转子系统及连续梁振动系统共振问题可靠性。安利强等[12]基于蒙特卡洛法分析随机裂纹叶片频率的概率敏感性及抗共振可靠度。此类研究均以固有频率落入激振频率一定范围发生共振失效为依据建立结构共振失效功能函数,未涉及激振频率变化。高速电梯轿厢系统外界导轨的激振频率是变化的,因此,考虑轿厢系统设计参数的随机性,基于摄动技术推导轿厢系统随机参数与系统频率响应间关系式,并据振动稳定性准则建立基于激振频率变化的系统共振失效功能函数,结合灵敏度理论研究轿厢系统设计参数对共振失效的灵敏度。
1随机参数轿厢系统振动方程构建
在水平方向滚动导靴起固定轿厢作用。将导靴系统简化为弹簧-阻尼系统,只考虑轿厢的水平振动与摆动。设m为轿厢质量,J为轿厢摆动的转动惯量,c为导靴系统阻尼,k为导靴系统刚度,y为轿厢水平位移,y1、y2、y3、y4分别为导靴1、2、3、4水平位移,θ为轿厢摆动角位移,l1、l2分别为导轮1与导轮3及导轮2与导轮4到质心的垂直距离。振动模型[13-14]见图1。
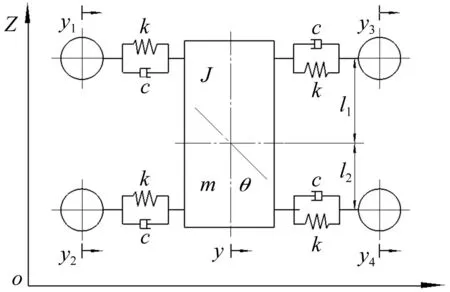
图1 二自由度轿厢系统振动模型 Fig.1 Model of vibrations for two DOF elevator cabin systems
据图1,轿厢系统动力学方程可表示为
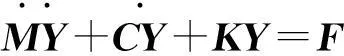
(1)
式中:M,C,K为轿厢系统质量、阻尼及刚度矩阵;F为外界载荷向量。
轿厢系统存在设计参数与激振载荷的随机性,使M,C,K,F也具随机性。据摄动理论[15],将M,C,K,F进行变换得
(2)
式中:ε为小参数;含下标d的部分为确定部分;含下标p的部分为随机部分。
将式(2)代入式(1),有
[Kd+εKp]Y=[Fd+εFp]
(3)
因此具有随机参数的轿厢系统振动方程为
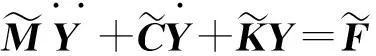
(4)
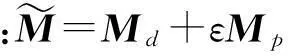
2轿厢系统固有频率与随机参数关系
大多固有频率分析仅限于确定参数的轿厢系统,忽略设计参数的随机性。由式(4)知,轿厢系统设计参数的随机性会导致系统固有频率ω具有随机性。对随机性描述由随机变量的数字特征体现。
设X=[x1x2…xn]T为系统随机参数,其与固有频率可表示为
X=Xd+εXp
(5)
ω=ωd+εωp
(6)
式中:随机部分具有零均值,取ε=1[16]。
据式(4),具有随机参数的轿厢系统特征方程为
(7)
式中:ω为系统固有频率;T(ω,X)为关于随机参数及固有频率的多项式。
将系统随机参数代入式(4)可得T(ωd,Xd)=0。将函数T(ω,X)=0在(ωd+εωp,Xd+εXp)处进行多元泰勒展开,并去掉高次项,得
(8)
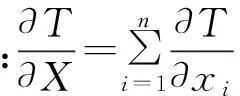
由于随机部分有零均值,对式(8)取期望得
(9)
3随机参数轿厢系统共振可靠性灵敏度分析
灵敏度作为设计的重要指标,所给设计参数对系统输出有重要影响。轿厢系统在运动过程中不可避免受导轨激励作用,固有频率与激振频率接近时会引起系统共振。因此找出对系统共振失效有较大影响的参数且严格控制,可避免轿厢系统发生共振。
3.1基于激振频率变化的共振失效功能函数建立
传统共振可靠性问题一般将固有频率与激振频率差值关系式定义为功能函数,即g(f,ω)=ω-f。其中f为激振频率。从此式不难看出,传统共振可靠性分析将激振频率视为定值,只要保证固有频率与确定的激振频率差值在一定范围即为可靠。而对轿厢系统,导轨对系统的激振频率不断变化,即外界激振频率存在上限值f1、下限值f2,故轿厢系统共振可靠性分析的功能函数并非固有频率及激振频率简单差值关系。
据振动稳定性准则[17],固有频率及激振频率满足关系为
1.15ω-f<0或0.85ω-f>0
(10)
式中:f,ω分别为激振频率、固有频率。
轿厢系统欲满足式(10),激振频率下限值须f2>1.15ω,或上限值须f1<0.85ω。因此,基于激振频率变化的系统共振失效功能函数定义为
g(f,ω)=(f2-1.15ω)(f1-0.85ω)
(11)
式中:f1,f2分别为激振频率最大、最小值。
据式(11)可确定随机参数系统发生共振的失效状态,即
g(f,ω)>0,(振动安全)
g(f,ω)≤0,(振动失效)
3.2共振可靠性灵敏度分析
据 式(11),系统固有频率、激振频率独立服从标准正态分布,按随机变量数字特征值性质[18]计算功能函数均值及方差,即
μg=μg1μg2
(12)
(13)
式中:
μg1=(μf1-0.85μω);μg2=(μf2-1.15μω)
轿厢系统共振可靠性指标为
(14)
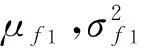
对轿厢系统防共振问题,据定义[19]获得可靠度对设计参数均值、方差灵敏度表达式,即
式中:
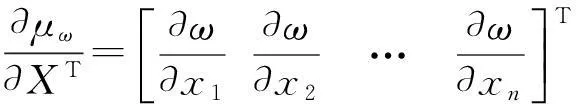
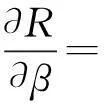
将可靠性分析计算结果及算例已知条件代入灵敏度表达式,用MATLAB软件可获得轿厢系统共振可靠性灵敏度。
4轿厢系统实例分析
4.1随机参数轿厢系统固有频率计算
据图1,轿厢系统振动模型的设计参数包括质量参数m、J,动力学参数k,几何参数l1、l2。基本随机变量为
X=[x1x2x3x4x5]T=[mJkl1l2]T
据式(4),二自由度轿厢系统随机多项式为
某型号高速曳引式直梯,运行速度v=5 m/s,各参数前两阶矩统计值见表1。
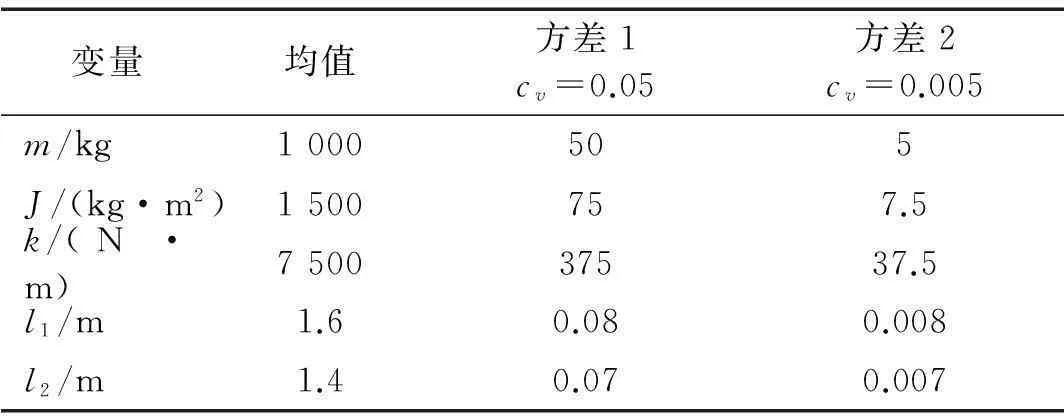
表1 高速电梯轿厢系统参数取值
可认为轿厢系统各随机变量相互独立且均服从标准正态分布。分别取变异系数cv=0.05,cv=0.005。利用所建基于摄动技术的轿厢系统固有频率随机性表达式,分别采用确定性及随机性模型计算轿厢系统固有频率。在确定性模型中,将所有随机参数的变异系数取为零;在随机性模型中,考虑设计参数为随机变量。结果对比见表2。由表2可知,①随机性、确定性两种模型的计算结果有差异。轿厢系统确定模型的固有频率输出仅为确定值;随机模型的固有频率有一定分散性。②考虑系统设计参数随机性,随机设计参数变异系数改变对轿厢系统固有频率随机性计算结果有较大影响,即系统固有频率分散性随设计参数变异系数增大显著增大。

表2 结果对比
据轿厢系统固有频率随机性,基于可靠性灵敏度理论,将轿厢系统随机固有频率分析问题转化为共振可靠性灵敏度问题。
4.2轿厢系统设计参数对共振失效灵敏度
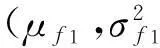
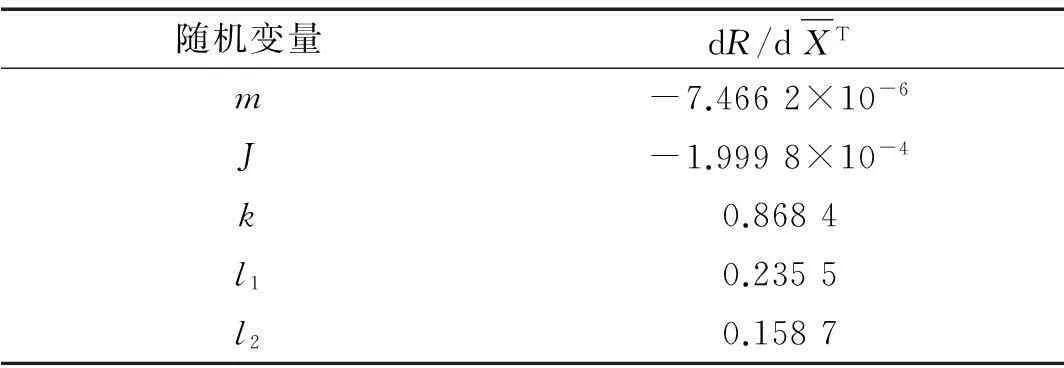
表3 可靠度对随机变量均值可靠性灵敏度分析结果
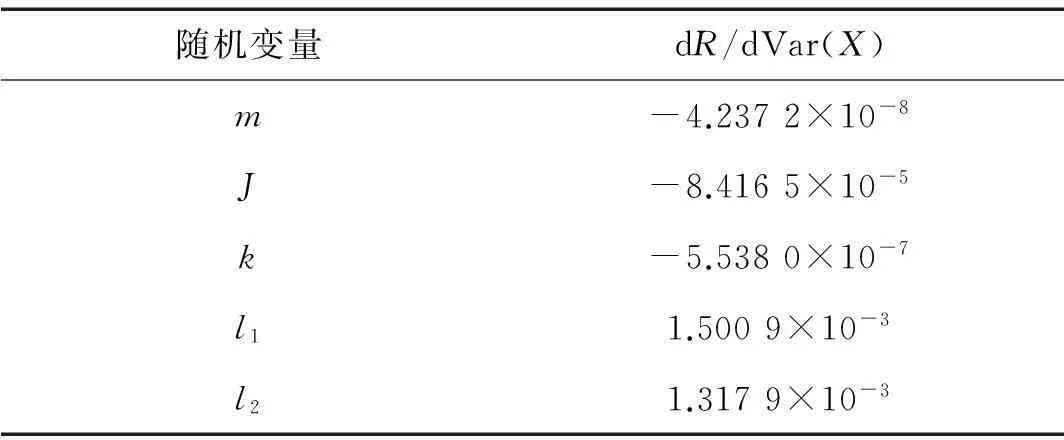
表4 可靠度对随机变量方差可靠性灵敏度分析结果
5结论
(1)本文基于参数随机性分析了轿厢系统固有频率随机性,通过与确定性轿厢系统模型对比,确定模型仅为随机模型中各随机参数变异系数为零的特例,且考虑参数随机性更符合轿厢系统实际工况;
(2)据导轨激振频率变化,基于振动稳定性准则建立的轿厢系统共振失效功能函数,能更准确描述轿厢系统运行中抑制共振的可靠性水平及确保高速电梯轿厢系统固有频率以合理的概率偏离导轨激振频率;
(3)通过对轿厢系统共振可靠性灵敏度分析,有效反映轿厢系统设计参数对共振失效的影响程度。在轿厢系统结构设计中,须严格控制敏感性较大的参数。从可靠性理论角度研究轿厢系统共振失效,可为电梯共振的预防、设计参数优化提供参考。
参考文献
[1]Utsunomiya K, Okamoto K I. Active roller guide system for high-speed elevators [J]. Elevator World, 2002, 50(4): 86-93.
[2]Funai K. The development of active vibration damper for super high-speed elevators [J]. Lift Report, 2004(5): 22-37.
[3]冯永慧,张建武. 高速电梯水平振动模型的建立与仿真[J]. 上海交通大学学报, 2007, 41(4):557-560.
FENG Yong-hui, ZHANG Jian-wu. The modeling and simulation of horizontal vibrations for high-speed elevator[J]. Journal of Shanghai Jiaotong University, 2007, 41(4): 557-560.
[4]梅德庆,杜小强,陈子辰. 基于滚动导靴-导轨接触模型的高速曳引电梯振动分析[J].机械工程学报,2009,45(5): 264-270.
MEI De-qing, DU Xiao-qiang, CHEN Zi-chen. Vibration analysis of high-speed traction elevator based on guide roller-rail contact model[J]. Journal of Mechanical Engineering, 2009, 45(5): 264-270.
[5]尹纪财,芮延年,蒋黎明,等. 高速电梯多自由度水平动态特性及其仿真的研究[J]. 机械设计, 2011, 28(10): 70-73.
YIN Ji-cai, RUI Yan-nian, JIANG Li-ming, et al. Research on high-speed elevator MDOF horizontal dynamic characteristics and simulation [J]. Journal of Machine Design, 2011, 28(10): 70-73.
[6]夏冰虎,史熙. 导轨激励下电梯水平振动的动力学建模[J]. 机械制造与自动化, 2012, 41(5): 161-165.
XIA Bing-hu, SHI Xi.Horizontal vibrations of high-speed elevator with guide rail excitation[J]. Machine Building & Automation, 2012, 41(5): 161-165.
[7]杜小强,梅德庆,陈子辰. 高速曳引电梯时变模型与水平振动响应分析[J]. 浙江大学学报, 2009, 43(1): 148-152.
DU Xiao-qiang, MEI De-qing, CHEN Zi-chen. Time-varying element model of high-speed traction elevator and its horizontal vibration response analysis [J]. Journal of Zhejiang University (Engineering Science), 2009, 43(1): 148-152.
[8]翟红波,吴子燕,刘永寿,等. 两端简支输流管道共振可靠度分析[J]. 振动与冲击, 2012, 31(12): 160-164.
ZHAI Hong-bo, WU Zi-yan, LIU Yong-shou, et al.Analysis of resonance reliability for a simply supported pipe conveying fluid[J]. Journal of vibration and shock, 2012, 31(12): 160-164.
[9]翟红波,吴子燕,李宝辉,等. 含非均匀轴向流的输液管道共振可靠性灵敏度分析[J]. 固体力学学报, 2012, 33(5): 480-486.
ZHAI Hong-bo, WU Zi-yan, LI Bao-hui, et al. Analysis of resonance reliability sensitivity for pipes conveying non-uniform axial fluid[J]. Chinese Journal of Solid Mechanics, 2012, 33(5): 480-486.
[10]苏长青,张义民,吕春梅,等. 转子系统振动的频率可靠性灵敏度分析[J]. 振动与冲击, 2009, 28(1): 56-59.
SU Chang-qing, ZHANG Yi-min, LÜ Chun-mei, et al. Natural frequency reliability sensitivity analysis of a rotor system [J]. Journal of Vibration and Shock, 2009, 28(1): 56-59.
[11]吕春梅,张义民,刘宇,等. 连续梁弯曲振动系统可靠性频率灵敏度研究[J]. 振动与冲击, 2013, 32(18): 159-162.
LÜ Chun-mei, ZHANG Yi-min, LIU Yu, et al. Sensitivity analysis for frequency reliability of a random bending vibration system of continuous beam [J]. Journal of vibration and shock, 2013, 32(18): 159-162.
[12]安利强,赵怀璧,王璋奇. 随机裂纹叶片抗共振可靠度及概率敏感性分析[J]. 中国电机工程学报, 2010, 32(30): 71-76.
AN Li-qiang, ZHAO Huai-bi, WANG Zhang-qi. Antiresonance reliability and probabilistic sensitivity analysis for random cracked blade[J]. Proceedings of the CSEE, 2010, 32(30): 71-76.
[13]傅武军,朱昌明,张长友,等. 高速电梯水平振动模型及动态响应分析[J]. 机械设计与研究, 2003,19(6): 65-67.
FU Wu-jun, ZHU Chang-ming, ZHANG Chang-you, et al. Modeling and analyzing lateral vibration for high-speed elevators[J]. Machine Design and Research, 2003,19(6): 65-67.
[14]李立京,李醒飞,张国雄,等. 电梯轿厢水平振动模型[J]. 起重运输机械, 2002(5): 3-5.
LI Li-jing, LI Xing-fei, ZHANG Guo-xiong, et al.Model of horizontal vibrations of elevator cage[J]. Hoisting and Conveying Machinery, 2002(5): 3-5.
[15]苏长青,张义民,马辉. 转轴裂纹扩展的可靠性灵敏度分析[J]. 航空动力学报, 2009, 24(4): 810-814.
SU Chang-qing, ZHANG Yi-min, MA Hui. Reliability sensitivity analysis for crack propagation of rotating shaft [J]. Journal of Aerospace Power,2009, 24(4):810-814.
[16]陈塑寰. 随机参数结构的振动理论[M]. 长春: 吉林科学技术出版社, 1992.
[17]秦大同,谢里阳. 现代机械设计手册(第6卷)[M]. 北京: 化学工业出版社, 2011.
[18]王玉孝. 概率论与随机过程[M]. 北京: 北京邮电大学出版社, 2003.
[19] 吕震宙,宋述芳,李洪双,等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.
[20]郭丽峰. 电梯导轨不平顺度测量、建模及轿厢水平振动特性的研究[D]. 天津: 天津大学, 2005.


