电磁轴承振动传递特性研究
第一作者莫逆男,博士,助研,1982年4月生
邮箱:moni@tsinghua.edu.cn
电磁轴承振动传递特性研究
莫逆,刘兴男,周燕,杨国军,时振刚
(清华大学核能与新能源技术研究院先进反应堆核工程与安全教育部重点实验室,北京100084)
摘要:通过有限元方法建立转子的仿真模型,结合电磁轴承动态模型获得整个电磁轴承支承转子闭环系统状态方程。基于该状态空间模型,计算转子受外扰力作用时轴承处力传递率频域响应、在外冲击力作用下位移响应及动态力响应,以此考察电磁轴承的振动传递特性,并与滚珠轴承进行对比。计算结果表明,电磁轴承的刚度阻尼等支承特性与滚珠轴承显著不同,其力的传递率频域响应较平缓,无滚珠轴承支承时某些频率附近的突出峰值。在冲击力作用下电磁轴承支承时,转子位移及动态轴承力振动均能较快恢复稳定状态,振动传递明显减小。
关键词:电磁轴承;状态空间模型;振动传递;冲击响应
收稿日期:2014-02-10修改稿收到日期:2014-03-27
中图分类号:TH133.3文献标志码:A
基金项目:国家自然科学基金资助项目(51075244)
Vibration transmission characteristics of active magnetic bearings
MONi,LIUXing-nan,ZHOUYan,YANGGuo-jun,SHIZhen-gang(Institute of Nuclear and New Energy Technology, Tsinghua University, the Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education, Beijing 100084, China)
Abstract:The simulation model of a rotor was obtained with the finite-element-method, and the dynamic model of an active magnetic bearing(AMB) was built. Then, the state-space model of an AMB-rotor system was constructed. With this state-space model, the frequency domain responses of the force transmission rate at the locations of bearings under external disturbance were calculated, and the impulse responses of the rotor displacements and the dynamic bearing force response were simulated too. The vibration transmission characteristics of AMB were studied and compared to those of rolling-ball bearings. It was shown that the stiffness and damping features of AMBs are quite different from those of roll-ball bearings; the frequency domain response of the force transmission rate is quite flat without sharp peaks around some frequencies using roll-ball bearings; with AMBs, the impulse responses of rotor displacements and the dynamic bearing force return to a stable state sooner than those do with rolling-ball bearings, and the vibration transmission is reduced obviously.
Key words:active magnetic bearing (AMB); state-space model; vibration transmission; impulse response
轴承作为连接旋转机械转子与基座的部件在振动传递过程起关键作用。实际中存在多种作用于转子的振动激励,如转子不平衡力及负载或工质等引入的外部激励力[1]均通过轴承向基座传递,引起振动。研究轴承的振动传递特性对预测振动[2-3]、探索振动控制方法具有重要意义。
电磁轴承能实时测量转子位置,通过设计的控制算法驱动电磁铁产生所需电磁力使转子悬浮,具有无机械接触、无摩擦、低损耗、无需润滑等优点,广泛用于气体输送、高真空设备、储能装置等领域[4]。电磁轴承因具有主动控制特点,其支承特性很大程度上由控制算法及参数决定,可据系统需要灵活配置,故使其对旋转机械的振动控制有巨大应用潜力[5]。
本文研究集中于电磁轴承的振动传递特性。结合转子有限元模型及电磁轴承控制器模型,建立转子-电磁轴承闭环系统状态方程。基于该状态空间模型,在频域上计算转子某节点施加动态激励力时,轴承的力传递率频域响应;并假设转子某位置施加冲击激励力,仿真计算轴承处传递动态力的时域波形。为进行对比,本文亦计算相同情况下滚珠轴承的振动传递。频、时域结果均表明,电磁轴承可有效减少转子振动向基座的传递。
1转子-电磁轴承系统模型

图1 五自由度转 子-电磁轴承系统 Fig.1 5-DOF AMB-rotor system
完整的电磁轴承-转子系统包括4个径向自由度及1个轴向自由度,见图1。通常,轴向自由度可与4个径向解耦单独考虑。本文仅考虑4个径向自由度。
电磁轴承任一自由度均含位移传感器、控制器、功率放大器、电磁铁及转子,组成闭环系统,见图2。通过分析系统中各部分获得闭环系统数学模型。

图2 电磁轴承闭环系统组成 Fig.2 Components in the AMB-rotor system
1.1转子
将转子离散成有分布质量及弹性的轴段及只有质量的圆盘,可得转子的有限元模型[8]。转子的运动方程可写为

(1)
式中:M为质量矩阵;K为刚度矩阵;D为阻尼矩阵;G为陀螺矩阵;Ω为转子角速度;F为转子上作用力;q为转子自由度,为单元自由度集合。
转子单元数越多其运动方程阶数越高,不便进行闭环系统分析及控制设计,因此须对转子模型进行降阶。本文采用模态截断方式,据研究需要选取某频率,略去高于该频率模态,获得系统降阶模型[9]。降阶过程可通过变换矩阵T描述,使
q=Ta
(2)
且

(3)

该模型等号左侧相当于自由转子动态方程,右侧为转子上作用力,包括轴承作用力、负载力、外部扰动力及等效不平衡力。将模型转化为状态方程模型,可得自由转子的状态空间模型。
令
(4)
则模型为
(5)
式中:
1.2电磁轴承
电磁轴承系统含电磁铁、功率放大器、位移传感器和控制器等部分,其电磁铁通常为差动结构,即由位置相反的两个电磁铁控制一个自由度(图2),其电磁力计算式为
(6)
式中:k为取决于轴承结构的常数;i0为静态偏置电流;x为转子位移;i为控制电流;s0,α见图2。
电磁轴承正常工作时i,x相对较小,可在工作点对式(6)求导,即
Δf=-ksx+kii
(7)
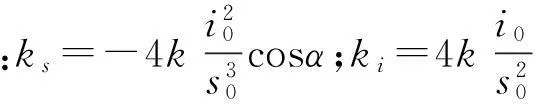
将式(6)线性化所得式(7)轴承作用力与转子位移及控制电流间线性关系,利于电磁轴承分析及控制设计,其有效性已获得实践检验。

图3 功率放大器控制框图 Fig.3 Block diagram of power amplifier
功率放大器用于产生驱动电流,本文考虑电流型功放,电流环采用最简单、最常用的比例反馈控制,见图3。其传递特性为
(8)
位移传感器将转子相对轴承位置转换为电信号供给控制器,通常为低通环节。本文选某实际电感式位移传感器,传递特性为
(9)
工程中常用的电磁轴承控制器为PID结合相位补偿[10],本文所用控制器传递函数为
(10)
综上可得电磁轴承一个自由度的数学模型,输入为转子位移,输出为电磁力。其状态空间形式为
(11)
式中:qb={x1b,x2b,x1s,x2s,y1b,y2b,y1s,y2s};Fb={fx1,fx2,fy1,fy2}
1.3闭环系统模型
在刚性基础假设下,结合电磁轴承模型及转子有限元动力学方程,可得闭环系统分析模型,见图4。其中,Prot为转子模型,Gamb为电磁轴承模型,d为轴承力以外的外部扰动力。作为电磁轴承-转子系统特有问题,转子稳定性及性能很大程度上由控制器结构与参数决定。而实际系统经参数调试才能获得稳定的闭环系统;不同参数下闭环系统性能差别较大,本文仅对比某一组使闭环系统稳定的控制参数。
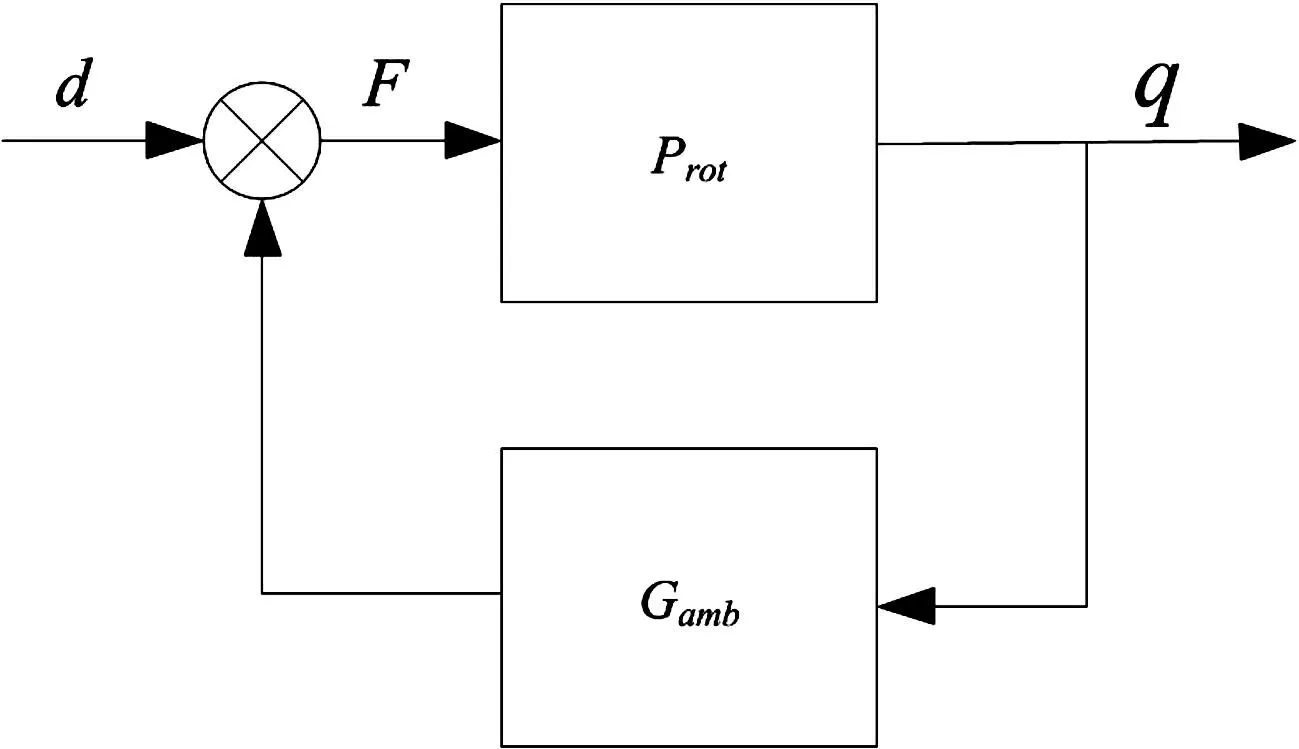
图4 电磁轴承闭环系统与振动传递模型 Fig.4 Block diagram of closed-loop bearing-rotor system
1.4电磁轴承振动传递特性
转子上的不平衡力或负载力等可等效成作用于转子的某个节点的外力,用d表示(图4),而电磁轴承与基座间作用力为Fb。在频域考察闭环系统从外扰力d到轴承力Fb间的传递特性,计算力传递率即可评价电磁轴承的振动传递特性。在时域计算d为冲击力时,动态轴承力Fb的波形亦可从另一角度考察轴承的振动传递特性。
为对比研究振动传递特性,本文同时建立滚珠轴承支承转子仿真模型。对滚珠轴承,图4的闭环模型同样适用,但传递特性不同,即
(12)
式中:k为轴承刚度系数;d为阻尼系数。
需说明的是,滚珠轴承在转子动力学分析中通常用恒定刚度、阻尼模型,而实际上滚珠轴承刚度随载荷变化,阻尼更复杂,尚无统一建模方法[11]。本文对滚珠轴承本身特性不作研究,仿真模型用恒定刚度、阻尼,具体数值据经验选取。
2仿真分析
2.1模型与降阶
用于仿真分析的转子由某设备转子简化而来,转子总长623 mm,质量18.7 kg,径向4个自由度轴承及4个位移传感器均标出,见图5。图中蓝色为转子芯轴,红色为等效圆盘。对滚珠轴承支承模型,轴承位置与电磁轴承位置完全相同,区别在于滚珠轴承无需位移传感器。滚珠轴承刚度系数为1×107N/m,阻尼系数为100 N·s/m。

图5 转子有限元模型 Fig.5 Finite-element model of the rotor
转子离散成59个节点,每个节点含4个自由度,完整模型计236个自由度。降阶前自由转子状态方程阶数为472。降阶时仅保留系统频率最低的12个模态。此处模型为计及x-z平面与y-z平面的多输入-多输出模型,相当于x-z平面与y-z平面内各保留4个模态。降阶模型与完整模型从fx1到x1b的传递特性对比见图6。由图6可知,转子600 Hz以下的动态特性几乎一致,从第3个挠性模态开始才有明显差异。说明用降阶模型研究较低频率下轴承振动传递特性是有效的。降阶后自由转子状态空间模型为16阶。

图6 降阶前后转子动态特性 Fig.6 Dynamic characteristic of rotor models before and after modal reduction
2.2轴承支承特性
本文所选电磁轴承控制参数见表1,开环下电磁轴承与滚珠轴承的支承特性对比见图7。图中黑线即为典型的磁轴承支承特性,值得注意的是:①在0 Hz附近,因积分控制的存在,支承刚度可远大于滚珠轴承;②而在较低频段(约0~500 Hz),也是一般的工作转速所在频率范围,电磁轴承的支承刚度较滚珠轴承明显低;③在低频段(约0~600 Hz),由于微分、相位超前等控制原因,电磁轴承可提供更多的相位超前,在物理意义上表现为提供更充分的阻尼。
2.3轴承传递力频域响应
考察动态外扰力作用下轴承传递力的响应,输入为从轴上598 mm处(图5中f1)作用的外扰力,输出为轴承处的力传递率。考察频率范围0~600 Hz。轴承1、2处力的传递率响应见图8、图9。由两图看出,在每个自然频率处,滚珠轴承均存在较高的力传递率尖峰。轴承1最高值在160 Hz处约60,轴承2在262 Hz时达92。而电磁轴承的力传递率会在自然频率处有所增加,但总体上较平缓。轴承1处最大力传递率出现在265 Hz附近约1.1,轴承2处为5,出现在267 Hz附近。

表1 电磁轴承参数


图7 电磁轴承和滚珠轴承的支承特性Fig.7BearingcharacteristicofAMBandrolling-ballbearing图8 外扰力f1到轴承1作用力幅频响应Fig.8Frequencydomainresponsefromdisturbancef1todynamicforceofbearing1图9 外扰力f1到轴承2作用力的幅频响应Fig.9Frequencydomainresponsefromdisturbancef1todynamicforceofbearing2

图10 冲击力f1引起轴承1处转子位移响应Fig.10Impulseresponseoftherotordisplacementatlocationbearing1whentherotorsubjectedtoimpactforcef1图11 冲击力f1引起轴承2处转子位移响应Fig.11Impulseresponseoftherotordisplacementatlocationbearing2whentherotorsubjectedtoimpactforcef1图12 冲击力f1引起的轴承1处轴承作用力响应Fig.12Impulseresponseofforceofbearing1whentherotorsubjectedtoimpactforcef1
2.4轴承传递力冲击响应
设在图5中f1位置施加一个半正弦波的冲击外扰力,峰值为5 000 N,作用时间0.2 ms。通过时域仿真获得两个轴承处转子位移响应分别见图10、图11。两个轴承处传递的作用力分别见图12、图13。对滚珠轴承,无论转子位移响应或轴承动态力响应,在冲击后的0.1 s内均存在较明显振荡,且衰减慢。而对电磁轴承,在冲击发生0.02 s后转子位移及动态力均衰减至零。此因在机电振荡频率范围内电磁轴承较滚珠轴承提供的阻尼更大,使冲击力所致振动快速衰减,恢复稳定状态。

图13 冲击力f 1引起的轴承2处轴承作用力响应 Fig.13 Impulse response of force of bearing 2 when the rotor subjected to impact force f 1
3结论
本文基于转子有限元模型及电磁轴承动态模型,获得电磁轴承-转子闭环系统状态方程,通过仿真计算,研究电磁轴承的支承特性及振动传递特性。结论如下:
(1)电磁轴承系统具有主动控制特点,其刚度及阻尼特性有别于滚珠轴承,表现为在通常的工作转速范围内具有较低刚度及较大阻尼。
(2)考虑转子上扰动力向基座传递时,滚珠轴承的力传递率在某些频率附近存在突出峰值,而电磁轴承的曲线较平缓,无特别突出峰值。
(3)转子上作用有冲击性扰动力时,电磁轴承支承的转子位移振动及动态轴承力均能迅速恢复稳定,减少振动时间及振动力的传递。
(4)电磁轴承的振动传递特性与控制方式及控制参数选取有较大关系,尚待研究。本文中基础假设为刚性,弹性基础需更深入研究。
参考文献
[1]蒋爱华,章艺,靳思宇,等. 离心泵叶轮流体激励力研究[J]. 振动与冲击, 2012, 31(22): 123-127.
JIANG Ai-hua, ZHANG Yi, JIN Si-yu, et al. Fluid exciting forces of a centrifugual pump on impeller[J]. Journal of Vibration and Shock, 2012, 31(22): 123-127.
[2]孙谦,钱大帅,陈明. 滑动轴承油膜的振动传递特性[J]. 舰船科学技术, 2013, 35(7): 71-73.
SUN Qian, QIAN Da-shuai, CHEN Ming. Vibration transmission characteristics of oil film in journal bearing [J].Ship Science and Technology, 2013, 35(7): 71-73.
[3]张秀芳,霍睿,周振,等.滚动轴承支承的齿轮传动轴-板耦合结构功率流传递特性研究[J].振动与冲击,2013,32(9):63-67.
ZHANG Xiu-fang,HUO Rui,ZHOU Zhen, et al.Transfer characteristics of power flow of the shaft-plate coupled sructure in gear driving system supported by rolling bearings [J].Journal of Vibration and Shock,2013,32(9):63-67.
[4]Schweitzer G, Maslen E H. Magnetic bearings: theory, design, and application to rotating machinery[M]. Berlin: Springer-Verlag, 2009.
[5]刘彬,房建成,刘刚,等. 磁悬浮飞轮不平衡振动控制方法与试验研究[J].机械工程学报, 2010, 46(12):188-194.
LIU Bin, FANG Jian-cheng, LIU Gang, et al. Unbalance vibration control and experiment research of magnetically suspended flywheels[J]. Journal of Mechanical Engineering, 2010, 46(12): 188-194.
[6]陈小飞. 磁悬浮飞轮系统振动分析与抑制控制研究[D]. 北京:国防科技大学, 2011.
[7]张剀,戴兴建,张小章,等. 磁悬浮分子泵的振动抑制[J]. 真空科学与技术学报, 2013, 33(6):556-563.
ZHANG Kai, DAI Xing-jian, ZHANG Xiao-zhang, et al. Vibration damping of magnetic bearing turbo molecular pump[J]. Chinese Journal of Vacuum Science and Technology, 2013, 33(6):556-563.
[8]钟一谔,何衍宗,王正,等. 转子动力学[M]. 北京:清华大学出版社, 1987.
[9]Khulief Y A, Mohiuddin M A. On the dynamic analysis of rotors using modal reduction[J]. Finite Elements in Analysis and Design, 1997, 26: 41-55.
[10]李红伟,赵雷,石磊,等. HTR-10氦气气轮机电磁轴承系统控制器研究[J]. 核动力工程, 2008, 29(4):100-104.
LI Hong-wei, ZHAO Lei, SHI Lei, et al. Study on active magnetic bearing controller for HTR-10 helium turbine rotor [J]. Nuclear Power Engineering, 2008, 29(4):100-104.
[11]闻邦椿,顾家柳,夏松波,等. 高等转子动力学-理论、技术及应用[M]. 北京:机械工业出版社, 2000.


