国外学科科研绩效评估指数的文献回顾

单承伟++王红++张苏等

〔摘 要〕目前很多学者利用RSI，AI，RCR，Specialization Intensity Index等指数从论文数量，引用次数，篇均引文量等指标分析某一研究国家（机构）学科排名情况。本文通过对学科科研绩效评估指数的文献回顾，分析了RSI，AI，RCR，Specialization Intensity Index等学科绩效评价指数的适用性和不足。研究结果表明：在开展影响力评价时，学科绩效评估不应仅仅是单一指标的比较，还应该遵循坚持同类相比的原则。

〔关键词〕RSI，AI，RCR，Specialization Intensity Index；学科评估

DOI：10.3969/j.issn.1008-0821.2015.11.031

〔中图分类号〕G25073 〔文献标识码〕A 〔文章编号〕1008-0821（2015）11-0171-07

A Review of Subject Assessment Index

Shan Chengwei Wang Hong Zhang Su Yang Yuli

（Library，Dalian University of Technology，Dalian 116014，China）

〔Abstract〕Many scholars use RSI，AI，RCR and Specialization Intensity index to evaluate research institutes research performance. In this paper，it first provided an overview of a number of source normalization approaches，and then compared the advantage and disadvantage of these indexes.The results showed that different scientific fields had different citation practices.Citation-based bibliometric indicators need to normalize for such differences between fields in order to allow for meaningful between-field comparisons of citation impact.

〔Key words〕RSI，AI，RCR，Specialization Intensity Index；subject performance

如何为机构科研绩效寻找有意义的评估方法，呈现本机构的研究绩效现状与发展趋势，与其他机构间比较分析，以便更好地为学科发展提供依据是科研管理人员普遍关心的问题。很多学者利用RSI，AI，RCR，Specialization Intensity Index等一系列指数从论文数量、引用次数、篇均引文量等指标分析某一研究机构学科的排名情况。本文通过对学科科研绩效评估指数的文献回顾，以期为今后学科评估研究方法的发展提供借鉴。

1 RSI和AI指数

11 RSI指数

Balassa（1965）[1]提出了相对比较优势指数Revealed Comparative Advantage index（RCA）算法，指的是某国家某学科论文比率与全球某学科论文的相对比率，也被称为学科活跃性指数（Relative Specialization Index，RSI），算法如下：

RSI=Pis/PiPS/P

其中Pis是国家I在S学科发表的文章数，Pi是国家I在所有学科发表的文章数，Ps是全球在S学科发表文章总数，P是全球在所有学科发表的文章总数。RSI指数反映了某国家在某学科文章发表数量比较优势。RSI取值在[0，∞]之间，RSI=0表明某国家在S学科领域研究为空白；当RSI取值[0，1]表明某国家在S学科不具有比较优势；RSI=1表明某国家在S学科领域的研究等于世界平均水平；当RSI取值[1，∞]表明某国家在S学科具有比较优势。

12 AI算法

Frame（1977）[2]同样提出了利用某国家F学科论文比率与全球F学科论文的相对比率用以衡量学科发文绩效的Activity Index（AI）算法，算法如下：

AI（C，F）=PFC/∑FP〖〗TPC/∑TP

其中PFC是国家C在F学科发表的文章数，∑FP是全球在F学科发表文章总数，TPC是国家C在所有学科发表的文章数，（PFC）∑FP是全球在所有学科发表的文章总数。

根据RSI和AI算法的定义可知，二者的计算方式相同。

尽管RSI和AI指数可以衡量某国的某学科发文相对指标，但是RSI和AI在实际统计过程中受到两个因素影响：一个是某国家F学科论文比率与某国家所有学科论文相对比率值；一个是全球F学科论文比率与全球所有学科论文相对比率值，由于RSI和AI最大值是∞，造成了AI最大值是一个变量，所以利用AI指数只能进行同一时间，同一学科不同国家学科比较优势的比较。

2 RCR及其衍生指数

21 RCR指数

Schubert（1986）[3]在AI指数的基础上，进一步用学科被引频次衡量机构科研绩效，提出了Relative citation Rate（RCR）算法，算法如下：

RCR=∑observed citation rate∑expected citation rate

其中，observed citation rate指的是某国家（机构）某学科实际被引频次，expected citation rate指的是某学科平均被引频次。RCR取值在[0，∞]之间，当RCR取值[0，1]时，表明某国家在F学科被引不具有比较优势；RCR=1 表明某国家在某一学科领域的被引频次研究等于所在领域的平均水平；当RCR取值[1，∞]时，表明某国家某一学科领域在学科被引具有比较优势。Schubert尽管在AI指数的基础上，用学科平均被引频次对数据进行归一化处理，但是由于不同学科不同年代平均被引频次不一致，即有些学科的RCR最大值为10，有些学科的RCR最大值为100，学科基准线不一致，所以如果利用RCR指数将无从判断不同时间，不同学科的学科被引绩效的高低。endprint

Braun and Glnzel（1990，1996）[4-5]对RCR指数进一步延伸，提出Mean Observed Citation Rate：

RCR=∑mean observed ciation rate∑Mean expected citation rate=MOCRMECR

Mean observed citation rate指的是某国家（机构）某学科实际篇均被引频次，expected citation rate指的是某学科平均篇均被引频次。

VINKLER（1997）[6]在RCR指数的基础上，又进一步提出了学科相对引用次数Relative Subfield Citedness（RW）：

RW=CGFm·P

其中P是文章数总数，c是文章被引次数，GFm是论文m所在期刊的影响因子。

对于RW指数的优点，VINKLER（1997）[6]引用Schubert（1986）[3]建立的分布间MOCR和MECR直接的关系图（relational charts）加以解释。Schubert（1986）在图中取坐标轴X轴为expected citation rate，取y轴为expected citation rate，根据RCR定义，我们可以画出一条经过（0，0），倾斜角等于45°的斜线，当A位于斜线上方时，我们可以得出机构A的RCR>1，B位于斜线下方时，我们可以得出机构B的RCR<1，也是说通过直观图，我们可以清晰地看到MOCR与MECR的线性关系。

VINKLER（2012）[7]在Mean observed citation rate的基础上，提出了基于期刊影响因子的RCR指数：

RCR=MOCRMECR=1P∑Pi=1ci1P∑Pi=1GFi=ciGFi

其中P是文章数总数，ci是发表的文章的被引次数，GFi是论文i所在期刊的影响因子。在这里RCR指数反映了某篇文章基于引用和期刊影响因子的比较优势。尽管RW和RCR（2012）指数考虑了文献的来源期刊的影响因子对文章质量影响力的评估，期刊影响因子个别评价可以为我们在评价文章论文质量时提供的另一种参考指标。但是RW和RCR指数只单纯计算来源期刊的影响因子而存在没有考虑该论文引用文献对该论文影响力提升的缺陷。正如Moed所说[8]，文献被声望较高的期刊引用应较被一般期刊引用来得显著，因此，应赋予声望较高的期刊引用更多权重值。

22 CPP/FCSm，MNCS和f指数

De Bruin（1993）[9]将RCR变化为CPP/FCSm，称之为Crown indicator指数。指数定义如下：

CPP/FCSm=∑ni=1ci/n∑ni=1ei/n=∑ni=1ci∑ni=1ei

尽管CPP/FCSm被广泛使用来统计某机构的学科影响力[10]，但在2007年Lundberg[10]针对CPP/FCSm指数对于平均引用频次较高的文章以较高的权重的缺点进行了标准化修正，提出了item oriented field normalized citation score average指数（f）。定义如下：

f=（1/P）∑Pi=1（ci/[μf]i）

其中ci国家（机构）某学科某篇文章实际被引频次，μf某学科国家（机构）某学科某篇文章所在领域的平均被引频次，P为国家（机构）某学科发表论文数。Lundberg在f指数的基础上，又提出了item oriented field normalized logarithm-based citation指数（fz[ln]）对f指数进行了取对数处理，算法如下：

fz[ln]=（1/P）∑Pi=1（ln（ci+1）-[μf[ln]]i）/[σf[ln]]i

其中ci国家（机构）某学科某篇文章i实际被引频次，由于ci有可能等于0，因此Lundberg取ci+1，使得ci对数值有意义。μf[ln]i是国家（机构）发表的文章i所在学科的被引平均数对数值，σf[ln]i为μf[ln]i的标准差。也就是说，Lundberg提出的fz[ln]方法采用了学科标准化中的z-score方法，这是因为不同学科不同年代学科平均被引次数都有所不同，通过对平均引用次数的标准差计算，可以避免不同学科平均被引次数变化的不确定性，更加精确评估分属不同学科的学科引用次数在各自数据分布中相对位置的高低。同时，正如Colliander[11]所指出的，由于学科引用次数都是偏态分布，通过引用次数的标准差计算，可以避免数据的离散程度相差悬殊，使数据符合正态分布。另外fz[ln]不仅可以用于中观层次评价例如对于大学等科研机构的评价，而且可以用于微观层次评价例如对研究人员或者期刊的评价[12]。

CPP/FCSm在2010同样被Waltman[13]提出了质疑，他认为CPP/FCSm指数受学科平均引用数大小的影响，学科平均引用数越大，机构综合学科指数越大。因此，他提出了MNCS指数：

MNCS=1n∑ni=1ciei

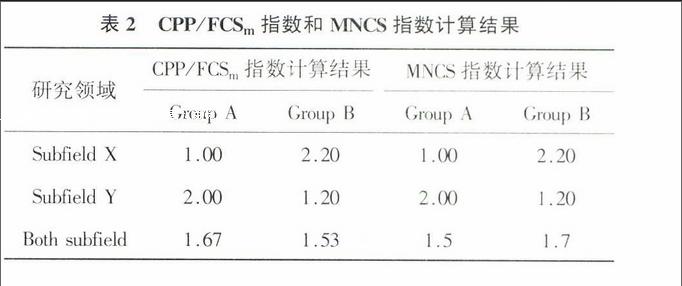
其中n为文章总数，ci为实际被引数，ei为平均被引数。假设有A，B两个机构的学科实际引用和文章总数以及平均被引数如表1[4]，根据CPP/FCSm=∑ni=1ci∑ni=1ei算法，则Research group A，B的两个学科领域的CPP/FCSm的计算结果为：

CPP/FCSgroup A=（1000/100+4000/100）/（10+20）=167

CPP/FCSgroup B=（2200/100+2400/100）/（10+20）=153

根据MNCS=1n∑ni=1ciei算法，则Research group A，B的两个学科领域MNCS的计算结果为：endprint

MNCSgroup A=（1000/100/10+4000/100/20）/2=15

MNCSgroup B=（2200/100/10+2400/100/20）/2=17

由表2计算过程可以看出，根据CPP/FCSm算法Research group A的学科指数值高于Research group B，根据MNCS算法Research group A的学科指数值低于Research group B。

Waltman[14]认为这是因为CPP/FCSm算法对expected citation高的学科赋予了更高的权重，也就是说CPP/FCSm=1n∑ni=1wiciei，其中wi=ei∑nj=1ej/n。通过对公式的解读我们发现，MNCS与f指数的计算方法相同。尽管MNCS对CPP/FCSm算法进行了修正，但是Leydesdorff[15]对MNCS指数的适用性提出质疑[15]：第一，ei的平均被引数是基于哪个标准？论文所在期刊的平均被引频次还是论文所属ISI数据库的学科平均被引频次；第二，如果论文所在的期刊分属不同ISI学科，例如期刊Journal of Vascular Research分属于ISI peripheral vascular disease和physiology两个学科，对平均被引频次将如何统计？第三，MNCS数据分布存在偏态分布的现象。由于MNCS算法存在以上缺点，Leydesdorff[15]提出，MNCS指数需要结合其它指数进行学科数据的综合评价，例如利用学科被引中位数代替学科被引平均数。或者利用Fraction counting计算方法，即每篇论文的被引次数除以该论文引用文献的数量替代学科平均被引频次。Opthof认为[16]，基于学科领域平均被引频次归一化数据的统计还存在许多问题需要进一步探讨，不同的学科数据标准化方法将会对机构的学科绩效评价带来不同的评价结果。

3 基于Percentile impact class的E（x）指数

Bornmann在World Report of the SCImago Institutions Rankings 2011报告中提出了Excellence Indicator这一概念，即同领域、同年份处于全球被引用前10%的论文可以被定义为高影响力论文（Excellence Indicator）。在此基础上，Bornmann[17]提出了衡量一个机构影响力的百分位数的文献计量指标方法E（x）指数：一个机构出版的文献可以根据引用次数，分为6个等级：处于全球被引用前top 1%，处于全球被引用前99th-95th，处于全球被引用前95th-90th，处于全球被引用前90th-75th，处于全球被引用前75th-50th，小于全球被引用前50%。一个机构的E（x）指数定义为：

E（x）=∑kk=1x·p（x）

其中，E（x）是某研究机构绩效，x为某等级序号，P（x）为某等级内文章频次，k为等级数。

假设某研究机构A发表了156篇文章（见表3），根据各篇文章的引用次数，位于6个等级的文章篇数分别为43，22，33，21，23，14。根据E（x）指数的定义：某研究机构A的绩效为：

E（x）=1*（43/156）+2*（22/156）+3*（33/146）+4*（21/156）+5*（23/156）+6*（14/156）=31

通过对E（x）的计算可知，E（x）指数避开了利用算数平均数对不同领域的发文进行数据归一化，也就是说避开了各学科研究特点不同，而导致引用行为存在差异。采用了百分比分类法（Percentile impact class），因此不同学科，不同类型论文都可以根据所处学科被引频次等级的高低进行分类，然后进行比较。Leydesdorff[18]认为：E（x）分类法不仅可以用来评价机构学科绩效，而且可以用来评价期刊影响因子，作为Impact factor的补充。Rousseau[19]提出，基于6个等级的E（x）指数可以拓展为基于100的E（x）指数，即100th-99th为100，99th-98th为99，…2th-1th为1。ESI数据库也是根据按被引频次高低确定出衡量研究绩效的阈值，分别排出居世界前1%的研究机构、科学家、研究论文。算法与Rousseau提出的基于100的E（x）指数计算方法一致。

然而，Schreiber[20]在利用E（x）指数进行计算时，发现其存在一个问题：假设某研究机构B的论文发表和被引情况如表4，通过计算，我们可以提出机构B的研究绩效为19。现在再假设机构B某零被引文献的被引次数增加1次（表4），同时扩大数据的统计范围，则百分比指数排名等级出现了变化，之前10篇被引1～5次的论文在百分比指数排名等级出现了下降，仍位于1级，则根据公式，机构B的研究绩效为165。也就是说，在机构B发文数量不变，被引次数增加的情况下，其研究绩效反而降低，从19降低到165。因此Schreibe[20]认为：E（x）指数受到数据统计范围的干扰，从而使研究机构的绩效统计出现不一致的情况。

4 Specialization Intensity Index指数

Laursen（2000）[21]在RCR的基础上又提出了将卡方检验（Chi square）作为RCR指数的进一步拓展，用以衡量经济行业某个部门的专业化程度。所谓卡方检验，就是比较理论频数和实际频数的吻合程度或拟合优度问题，基本思路如下[21]：

x2=∑（A-E）2E

其中A代表某个类别的观察频数，E代表期望频数，A与E之差称为残差。由于偏差之和为0，所以需要对偏差进行平方。

Confraria（2015）[22]将卡方检验进行变换，称之为Specialization Intensity Index（SII），SII指数算法如下：endprint

SII=∑SXsi/∑SXsi-∑iXsi/∑s∑iXsi2∑iXsi/∑s∑iXsi

其中Xsi是国家i在s学科发表文章被引次数，∑sXsi是该全球在s学科发表被引次数总数，∑sXsi是国家i在所有学科发表文章被引次数总数，∑s∑iXsi是全球在所有学科发表文章被引次数总数。SII反映了某国家在i学科的文章影响力。SII具有以下优点：（1）不仅可以比较某个研究机构某个学科与世界上这个学科水平的差距，而且可以用来比较两个机构某个学科水平的差异。（2）SII指数也可以用来比较某个机构某个学科在不同时间的学科水平。但是SII也存在以下缺点[23]：（1）SII对极值比较敏感；（2）SII值的大小又跟子集大小有关，子集个数越多，SII也会越大。假设有两个分类变量X和Y，样本数据如表5：

根据计算公式，我们可以得到：

SII=n（ad-bc）2（a+b）（c+d）（a+c）（b+d）（其中，n=a+b+c+d）

由此可见，由于卡方校验的值SII受到n的影响，n越大，X2越大。

5 Yit指数

Pastor（2015）[24]提出了Yit指数，算法如下：

Yit=（No.Documents）it·（No.citation per documentsit）（No.citations per documentswt）

其中Yit代表某个机构i的t学科综合评价指数，NoDocumentsit指的是某机构学科发文数量，Nocitations per documentsit代表某个机构t学科篇均学科被引次数，Nocitations per documentswt代表全球t学科篇均学科被引次数，尽管Yit从学科发文和篇均被引两个方面综合评价了某机构学科的影响力，但是Yit存在数据标准化的问题：假设A机构学科发文篇Nat，总被引频次Cbt次，B机构学科发文Nat篇，总被引频次Cbt次，那么机构A，B的学科影响力哪一个大？根据Yit指数的定义，机构A，B的学科影响力分别为：

Yat-Ybt=Nat·CatNatNo.citations per documentswt-

Nbt·CbtNbtNo.citations per documentswt，因此，

Yat-Ybt=Cat-Cbt（No.citations per documentswt）

通过公式换算我们可以看出，A，B机构影响力Yit指数的不同为A，B机构总被引频次的差值，由于总被引频次受到机构规模以及学科的影响，即使对于同一学科，不同年代的学科篇均被引频次也不同，因此Yit同样无法比较不同机构，不同年代的学科影响力。

尽管以上各个学者从不同角度，利用不同方法对学科标准化指数提出了自己的观点（见表6），我们发现，学科标准化指数在设计上仍然需要考虑以下问题：

（1）学科标准化指数是否需要考虑文献类型对文章引用次数的影响[25]。我们知道综述由于能够较全面地罗列相关研究主题文献，详尽地论述相关领域的进展及特点，它能使读者快捷、全面地了解相关研究领域的研究水平和发展动态。所以，发表综述类文献引用率较高。因此，如何区分文献类型对文章引用次数的影响是我们在设计学科评价指标时应考虑的一个问题。

（2）一个机构学科发文和引用次数受到机构规模的影响，因此计算机构学科影响力不仅需考虑引用次数，还需考虑规模。一个机构科研人员越多，每年发表的文章篇数可能越多，学科引用次数可能越多，RSI，AI，RCR指数值可能越高。因此在分析机构学科指数时，不应忽略学校规模对科研成果的影响，正如Glnzel[26]所说，学科绩效评估不应仅仅是单一指标的比较，还应该遵循坚持同类相比的原则，需要对数据进行归一化处理。

（3）仅仅以发文或者引文次数作为机构学科影响力的指标是否过于单一[27]。随着网络的发展，学术文献的影响力已经不仅局限于某些数据库的被引数据。社交媒体的出现，论文被广泛地分享在科学博客、BBS论坛，维基百科、及其他社会媒体，因此，目前有学者利用全新的Altmetrics指标[27]：如Mendeley下载、tweet推荐、Facebook转发，html view，PDF view等指标对机构学科影响力进行评价。随着学术传播模式的转变，是抛弃传统机构评价指标或是两者配合使用，也是学者今后需要研究和讨论的一个问题。

6 结 语

随着数字环境的发展，如何结合传统以引用次数为主的学术评价方式，反映网络环境下的学术影响力。希望藉由本文引发更多的学者投入机构评价研究，以发展出更多具有参考价值的相关论文。学术评价本来就不存在最好的方法，永远只有相对参考价值。

参考文献

[1]Balassa B.Trade Liberalisation and“Revealed”Comparative Advantage[J].The Manchester School，1965，33（2）：99-123.

[2]Frame，JD..Mainstream research in Latin America and the Caribbean[J].Interciencia，1977，（2）：143-148.

[3]Schubert，A.，& Braun，T.Relative indicators and relational charts for comparative assessment of publication output and citation impact[J].Scientometrics，1986，9（5-6）：281-291.

[4]Braun，T.，Glnzel，W.United Germany：The New Scientific Superpower[J].Scientometrics，1990，19（5-6）：513-521.endprint

[5]Glnzel W.The need for standards in bibliometric research and technology[J].Scientometrics，1996，35（2）：167-176.

[6]Vinkler P.Relations of relative scientometric impact indicators.The relative publication strategy index[J].Scientometrics，1997，40（1）：163-169.

[7]Vinkler P.The case of scientometricians with the“absolute relative”impact indicator[J].Journal of Informetrics，2012，6（2）：254-264.

[8]Moed F.，H，EDe Bruin R，NVan Leeuwen T.New bibliometric tools for the assessment of national research performance：Database description，overview of indicators and first applications[J].Scientometrics，1995，33（3）：381-422.

[9]Bruin R E D，Kint A，Luwel M.A study of research evaluation and planning：the University of Ghent[J].Research Evaluation，1993：25-41.

[10]Lundberg J.Lifting the crown—citation z-score[J].general information，2007，（1）：145-154.

[11]Colliander C，Ahlgren P.The effects and their stability of field normalization baseline on relative performance with respect to citation impact：A case study of 20 natural science departments[J].Journal of Informetrics，2011，5（1）：101-113.

[12]Raan A F J V.Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgment for 147 chemistry research groups[J].Scientometrics，2006，67（3）：491-502.

[13]Waltman L，Eck N J V，Leeuwen T N V.Towards a new crown indicator：An empirical analysis[J].Scientometrics，2010，87（3）：467-481.

[14]Waltman L，Eck N J V，Leeuwen T N V.Towards a new crown indicator：Some theoretical considerations[J].Journal of Informetrics，2010，5（1）：37-47.

[15]Leydesdorff L，Opthof T.Remaining problems with the“New Crown Indicator”（MNCS）of the CWTS[J].Journal of Informetrics，2011，5（1）：224-2.

[16]Opthof T，Leydesdorff L.Caveats for the journal and field normalizations in the CWTS（“Leiden”）evaluations of research performance[J].Journal of Informetrics，2010，4（3）：423-430.

[17]Bornmann L，Mutz R.Further steps towards an ideal method of measuring citation performance：The avoidance of citation（ratio）averages in field-normalization[J].Journal of Informetrics，2011，5（1）：228-230.

[18]Leydesdorff L，Bornmann L.Integrated impact indicators compared with impact factors：An alternative research design with policy implications[J].Journal of the American Society for Information Science and Technology，2011，62（11）：2133-2146.

[19]Rousseau R.Basic properties of both percentile rank scores and the I3 indicator[J].Journal of the American Society for Information Science and Technology，2012，63（2）：416-420.endprint

[20]Schreiber M.Inconsistencies of Recently Proposed Citation Impact Indicators and how to Avoid Them[J].Journal of the American Society for Information Science and Technology，2012，63（10）：2062-2073.

[21]Laursen K.Do Export And Technological Specialisation Patterns Co-Evolve In Terms of Convergence or Divergence？Evidence From 19 OECD Countries，1971-1991[J].Social Science Electronic Publishing，2000，10（4）：415-436.

[22]Confraria H，Godinho M M.The impact of African science：a bibliometric analysis[J].Scientometrics，2015，102（2）：1241-1268.

[23]The Chi Square Statistic[EB/OL].http：∥math.hws.edu/javamath/ryan/ChiSquare.html，2015-03-30.

[24]Pastor，José Manuel.The research output of European higher education institutions[J].Scientometrics 2015，102（3）：1867-1893.

[25]Crespo J A，Ortu-Ortín I，Ruiz-Castillo J.The Citation Merit of Scientific Publications[J].Plos One，2012，7（11）：488-488.

[26]Glnzel W，JCzerwon H.A new methodological approach to bibliographic coupling and its application to the national，regional and institutional level[J].Scientometrics，1996，37（2）：195-221.

[27]Peters，Isabella.Altmetrics for large，multidisciplinary research groups：A case study of the Leibniz Association[C].Proceedings of Libraries in the Digital Age，2014：9-14.

（本文责任编辑：孙国雷）endprint