变径管与薄壁圆管轴向压缩过程研究

徐龙江，雷君相，高贵杰

（上海理工大学 材料成形与模具研究所，上海 200093）

0 引言

变径管作为一种有效吸能元件［1］受到广泛关注，国内外对其研究也越来越多［2］。变径管在受轴向压缩时，其内管和外管都受到力的作用［3］，各部分的变形模式有很多种，如自由翻转、内管和外管的轴对称或非轴对称失稳［4］等。为了能直观地研究变径管在轴向载荷作用下的变形过程，将变径管的内管、中管和外管抽象出来单独研究，其中内管和外管可以看作只受轴向压缩，中管受轴向拉伸。结合圆管轴向压缩，可以对变径管的变形过程作系统研究，从而为变径管在轴向压缩过程中出现自由翻转提供新的理论依据。

1 理论研究

变径管结构及轴向压缩过程如图1所示，在轴向载荷作用下，其内管和外管受到轴向压缩，中管受轴向拉神［5］。根据应力应变曲线，断裂强度大于屈服强度，因此中管拉断时的力应该远大于压缩内管和外管时的压力。因此本文研究的重点是薄壁圆管压缩和变径管自由翻转。变径管几何尺寸如表1所示。

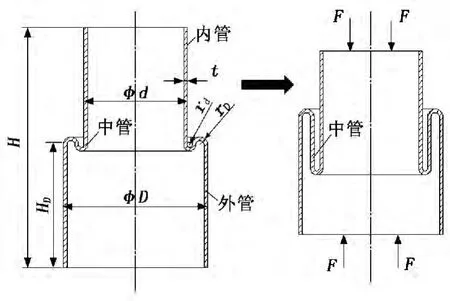
图1 变径管结构及轴向压缩过程

1.1 薄壁圆管轴向压缩载荷

当薄壁圆管受轴向压缩时，其塑性破损模式可能是轴对称或非轴对称形式，这主要取决于圆管外径和厚度之比（D0/t）。轴对称模式通常称为圆环模式，而非轴对称模式被称为钻石模式。一般而言，D0/t＞80的圆管发生钻石模式的破损，D0/t＜50时发生圆环模式的破损［6］。图1所示的变径管中，内管和外管的直径与厚度之比均小于50，在轴压下均发生圆环模式的破损。

表1 变径管几何尺寸

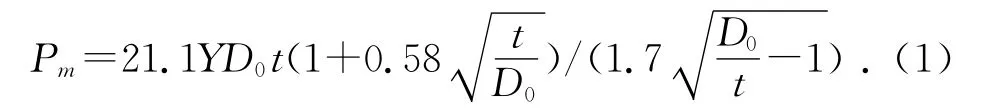
其中：Y为屈服应力。

金属薄壁圆管采用20钢，将Y＝296MPa、D0＝40mm、t＝1.4mm 代入式（1）中，得出压缩内管的平均载荷为47.9kN；当Do＝56mm时，得出压缩外管的平均载荷为54.7kN。

1.2 变径管轴向压缩载荷

变径管在轴向压缩作用下发生自由翻转，在自由翻转的稳定阶段，自由翻转力将达到最高值且保持不变［7］。由上海理工大学雷君相教授推导的变径管自由翻转吸能元件内管外翻的翻转力公式为：

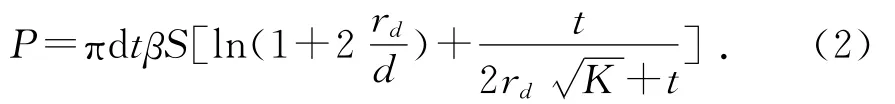
对于受轴向压缩的薄壁圆管而言，一般采用的理论模型是Alexander模型，即通过塑性铰来建立平衡方程，进行圆管轴对称压溃分析，得到完成整个褶皱过程的平均载荷Pm：

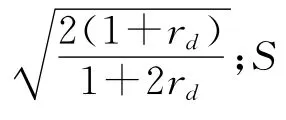
2 模拟研究

本文模拟采用薄壁圆管，其弹性模量为210GPa，泊松比为0.3，密度为7 800kg/m3。由于此次压缩模拟的位移较大，接触较复杂，故模拟实验采用ABAQUS/Explicit软件进行有限元分析，模型中圆管和变径管采用三维的可变形体，上、下压头均采用解析刚体，材料属性中输入圆管弹性参数和塑性参数，摩擦因数设为0.1。压缩圆管时要设置圆管的自接触，防止圆管发生穿透现象，使模拟结果更加真实。图2为所要压缩的薄壁金属圆管和变径管的有限元模型。

图2 圆管和变径管的有限元模型

为了比较压缩后的结果，设置压缩的位移量s＝30mm，薄壁金属管和变径管压缩的模拟结果如图3所示。

图3 圆管和变径管的压缩结果

从压缩结果可以看出：圆管受压缩发生轴对称失稳，其失稳模式为圆环模式，产生较为规则的褶皱；变径管经压缩后，内管和外管变形为中管，中管逐渐由短变长，整个过程比较稳定。

3 结果分析

圆管内管、圆管外管和变径管3种压缩过程的载荷－位移曲线如图4所示。从图4中可以看出，圆管内管和外管发生轴对称失稳时，载荷先达到一个最大的初始峰值，随后急剧下降，然后波动起伏，这些波动是由连续褶皱产生的，每一个峰值对应于一个褶皱过程的开始。

变径管自由翻转开始阶段，载荷随着加载位移的增加而增大，达到一个峰值，之后出现下降，最后会达到一个稳定值并持续进行下去。变径管自由翻转的载荷－位移曲线比较平稳，与模拟出现的中管平直稳定这一结果相吻合。并且变径管的载荷－位移曲线和圆管的载荷－位移曲线相比，多处于其下方，表明变径管翻转稳定时的载荷要小于压缩圆管时的载荷。

由于压缩圆管产生的载荷最大峰值远大于变径管自由翻转时产生的载荷最大峰值，因此，变径管在发生轴向压缩时更易发生自由翻转，而不会发生内管或者外管的轴对称失稳；根据载荷的平稳程度，变径管的自由翻转是理想的变形模式，可以作为吸能元件应用于各种碰撞场合。

表2为圆管压缩和变径管自由翻转的理论计算值和模拟结果对比。由表2可以看出，理论计算出的变径管自由翻转时的平均载荷和模拟结果基本吻合，模拟结果中自由翻转下的Pm是自由翻转过程中载荷稳定状态时的力。

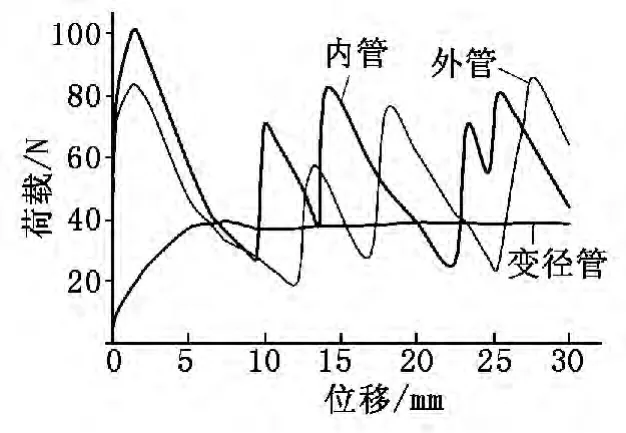
图4 圆管和变径管轴向压缩的载荷－位移曲线

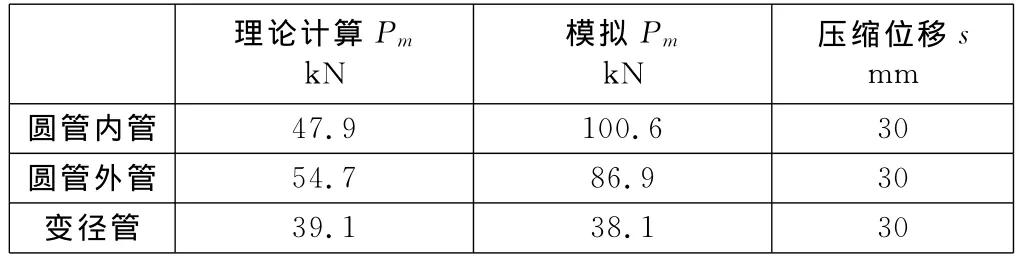
表2 圆管压缩和变径管自由翻转的理论计算和模拟结果对比

4 结论

（1）薄壁圆管压缩时的最大载荷远大于变径管自由翻转时的最大载荷。

（2）轴向压缩时，薄壁圆管发生轴对称失稳，变径管发生自由翻转，不会发生内管或者外管的轴对称失稳。

（3）变径管在发生自由翻转时的变形模式稳定，载荷随加载位移的增加保持恒定，可以作为理想的吸能元件。

（4）理论计算出的变径管自由翻转时的平均载荷和模拟结果基本吻合。

［1］Guillow S R，Lu G，Grzebieta R H.Quasi static axial compression of thin－walled circular aluminum tubes［J］.International Journal of Mechanical Science，2001，43：2103－2123.

［2］张立玲，高峰，杜发荣.不等厚拼焊管轴向压缩变形的数值模拟研究［J］.塑性工程学报，2006，13（4）：6－19.

［3］刘德学，何清和，袁文辉，等.薄壁圆管变形吸能元件准静态压溃吸能分析［J］.电力机车与城轨车辆，2011，34（3）：37－39.

［4］张立玲，林逸，高峰.不同材料薄壁圆管准静态轴压变形特性［J］.塑性工程学报，2010，17（4）：62－65.

［5］雷君相，李笠.圆管缩径能量吸收装置的研究［J］.塑性工程学报，1995，2（2）：57－64.

［6］余同希，卢国兴.材料与结构的能量吸收［M］.北京：化学工业出版社，2006.

［7］王敏杰，雷君相.变径管自由翻转过程研究［J］.热加工工艺，2013，42（5）：146－148.