基于GNSS动动差分相对定位方法的研究与探讨

汪捷，徐冠楠

（海军工程大学，武汉 430033）

0 引言

在高动态相对定位中，利用GNSS载波相位差分技术可以达到提高定位精度的作用，通过在动态基准站和流动站上各安装一台接收机，流动站上的接收机跟踪卫星信号，与基准站的接收机传递来的信号等信息进行载波相位双差处理，在正确解算整周模糊度的前提下，即可得到基准站与流动站之间的精确相对位置。与一般情况不同的是，此时的基准站处于运动状况，其和流动站一样坐标实时变化，为达到实时单历元求解整周模糊度，因此必须对传统载波相位差分技术在此情形下的问题进行分析研究。

1 GNSS 相对定位

采用两台或者多台接收，将其中一台接收机（基准站）固定于坐标精确已知的某点，同样选取另一点固定一台接收机，作为流动站。两台接收机同步跟踪一组卫星，同时采集观测数据，当满足卫星数目足够多时，流动站的接收机根据自身的观测数据和接收来自基准站的信息可以解算出自己的精确位置，这就是GNSS相对定位。

通常情况下，GNSS定位根据基准站发送的信息内容可以分为：位置差分、伪距差分和载波相位差分。载波相位差分的精度最高，因此本文着重讨论载波相位差分这一方法。

载波相位差分中有多种差分模型，比如单差、双差以及三差等。以双差为例：

以双差模型为主，短基线为例，经过双差之后，可以消除对流层，电离层，多路径等影响，简化模型为：

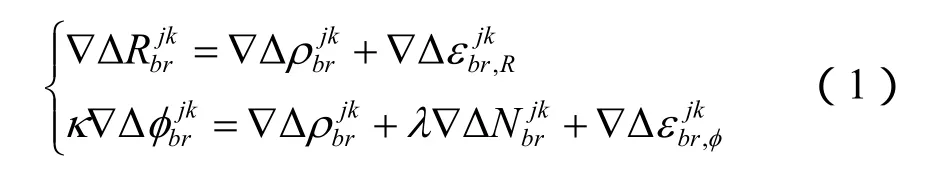
式中，j，k分别表示不同可见卫星；b，r分别表示基准站和流动站；ε为多路径噪声。

2 整周模糊度解算

由于在高动态动动定位过程中，不论是流动站还是相对流动站载体都在运动，静态情况下多历元解算固定模糊度的方法已经不能满足需求，其次在卫星信号受到影响之后造成无法快速固定模糊度时，必须寻找其他方法来解决此问题。依据传统求解的方法，具体可以通过以下两个步骤进行实现模糊度解算：首先，获得一个高精度的浮点解，其次建立一个快速的模糊度搜索方法。目前常见的快速模糊度解算方法有LAMBDA算法、最小二乘算法、快速模糊度逼近法（FARA）以及卡尔曼滤波方法等等。其中，在上述方法中，LAMBDA法是一种公认的有效方法，但是当卫星信号受到干扰造成观测质量较高的历元不多时，LAMBDA法解算过程中，法矩阵会出现秩亏，此时观测方程的系数矩阵将不可逆，无法得到准确的浮点解。因此在此基础上，针对上述问题，本文利用双频组合的方法构建新的包含整周模糊度参数和基线向量等参数的组合方程，利用线性组合和最小二乘方法求解基线向量和模糊度。

3 双频模糊度单历元解算方法

在单历元定位算法中，能否得到稳定可靠地定位结果，关键就是快速可靠地确定出正确的整周模糊度，本文基于双频数据单历元定位中存在观测时间短，观测量较少，提出一种分步消元的方法来确定整周模糊度。

分步消元求解整周模糊度包括两个方面：

（1）分步即先确定宽巷模糊度，然后逆求B1，B2模糊度；

（2）消去不必要求解的未知数，在组合方程中不必要的未知数即坐标参数。

基本过程是利用 MW 组合观测值联合宽巷观测值组成方程求解模糊度浮点解，再使用LAMBDA法搜索模糊度。当模糊度固定之后，再利用之前的组合关系确定B1和B2的模糊度，为了减小电离层影响，组合观测值表示的B1模糊度的解作为搜索标准，确定B1，B2的模糊度。

根据GNSS相对定位原理可知，在载波相位差分解算基线时，一旦模糊度正确固定，就能正确解算基线。下面采用双频组合的方法求解模糊度。设基准站和流动站同时可以观测到n颗卫星（n＞4），对其中两颗卫星i，j，在某一历元时刻可以得到任意两站1和2关于L1、L2载波的宽巷组合观测方程为

其中，λ为载波波长；φ为载波相位观测值；ρ为站星之间的距离；N为整周模糊度；ε为载波相位观测噪声；W表示宽巷。

对于宽巷载波，同样可以给出宽巷载波整周模糊度的最小二乘方程：

式中，X为基线矢量；N为双差模糊度向量；A、B为系数矩阵；C-1为权矩阵。下面假设双频载波相位的组合系数分别为α、β，可以得到组合载波相位值：

组合之后的相位模糊度Nαβ可以通过最小二乘方法求得，由于仅有α、β一组系数无法正确求解各自模糊度，因此再任意给一组系数η、γ构成如同上式的组合，即可以根据下面矩阵正确求解各自模糊度N1和N2。

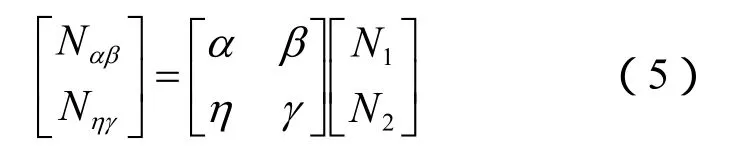
求解出模糊度之后，可以根据式（3）反求解基线向量。

4 试验验证

首先利用试验说明了传统的GNSS差分处理技术在卫星信号受到影响时所面临的问题，针对动动差分相对定位模型，提出几种测试方案，并利用相应的试验对所提算法进行验证。最后，利用该系统进行了实际场外试验，模拟动态相对运动，对系统性能进行了测试和评估。

首先选取空旷的场地，保证信号质量较好时进行测试，下面先对基准站移动时的情况作分析。

2.1 基准站移动对流动站定位结果影响

试验时间为为2014年5月28日，地点在电气院楼顶和田径场分别架设基准站和移动站，采用卓越航导有限公司的UB240型北斗差分接收机，数据更新频率为1Hz。

首先静态定位一段时间后，将基准站沿着事先的设定的基线方向做直线运动，流动站保持不动，在载波相位差分定位的模式下分析移动站的定位结果。下图为载波相位差分模式下的定位结果。

图1 载波相位差分模式下基站移动时移动站定位结果图

由图1可以看出，当基准站沿着事先的基线方向朝着流动站运动时，流动站的定位点越趋近，说明此历元时刻流动站与基准站定位结果的变化趋势相反。

2.2 高精度动动差分相对定位方法

（1）首先基准站、动态基准站和流动站同时接收卫星信号，提取卫星伪距和双频载波相位等原始观测量；

（2）基准站利用伪距单点定位方式进行实时定位，获取卫星原始观测信息；

（3）基准站将伪距单点定位的结果和自身观测到的卫星原始观测信息通过电台实时发送给移动站；

（4）移动站提取自身和基准站共同观测到的卫星原始观测信息进行双频组合单历元模糊度求解，实时解算相对基线矢量，并保存结果；

（5）移动站根据基准站伪距单点定位结果和计算得到的相对基线矢量，利用上述提出的算法实时输出移动站位置和基线信息，从而分析偏差验证本文算法的有效性。

2.3 动动差分试验方案

为了验证动动差分相对定位方法的性能和指标，采用以下两种试验方案。

方案一：准动态对动态测量方法。首先选取几个点，采用较长时间的绝对单点定位方式确定其位置，将基准站和移动站接收机分别停留较长历元，采集其同步观测数据，换几个观测点重复采集。将此方法计算确定的两个观测点之间的相对位置，与标准基线值比较以衡量定位精度。

方案二：动态对动态测量方案。这种方案采用三台接收机，分别记为基准站，移动基站和移动站。首先将第三台接收机静止作为静态基准站，与移动基站进行常规载波相位差分，可以测得移动基站的精确绝对位置，采用同样的方法可以得到移动站的精确绝对位置。利用以上两个绝对位置通过标准RTK算法可以计算动态对动态差分两站之间的相对基线位置，将该相对位置值作为差分测量的标准值。同时利用本文算法将解算的相对基线位置与该标准值进行比较，验证本文算法的可靠性。

a.准动态对动态定位实验

实验前首先将接收机定位模式设置为伪距单点定位模式，选三个点分别作为基准站，移动基站和移动站测试点，在每个点分别静态定位 20min，将定位的平均值作为测试点坐标真值，测试点的定位结果均值如表1所示。

由测试点 1,2,3三个点构成的基线向量分别记为（1,2）、（2,3）、（1,3），其在空间直角坐标系下坐标分量以及长度如表2所示。

将选定的基准站和移动站分别架设于测试点 1与3，首先静态测试一段历元（大于10个）数据，保持支架不动，在测试点1和3重复同样的的操作，之后将接收机移动到测试点2和3处，按照上述步骤重复操作。在每个测试点试验过程中，尽量保证测试点的天线中心的位置尽量相同，实验过程中记录原始数据。整个实验过程中的测试时间为30min，共计400个历元时刻。运用单历元求解方法对上述过程进行基线解算，可解算得出基线向量分量及长度的变化。下面对其中的第一条基线进行分析，给出编号（1,3）的基线分量及长度变化图。

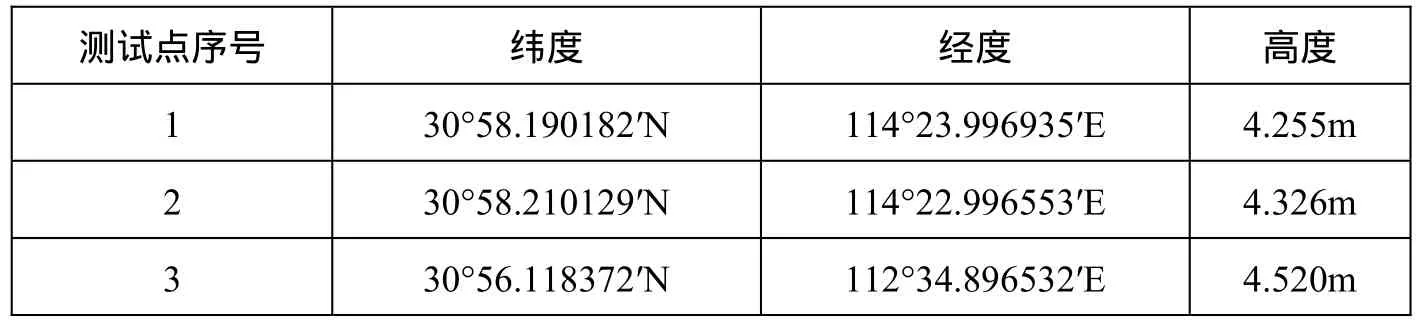
表1 三个测试点的位置坐标

表2 三条基线向量三维分量以及长度

图2 基线（1,3）向量分量以及长度变化

为了更有代表性地分析数据，现选取中间 50个历元数据进行分析，与表2中的标准值进行对比，可得每个历元的基线分量和长度误差如图2所示。

与表2中的标准值作对比，可得每个历元时刻的基线分量和长度误差，如图3所示。

图3 基线（1,3）向量分量与长度误差

由图可见，所有 50个单历元中，基线向量长度L偏差小于3.5cm其中X、Y方向分量偏差小于3cm，Z方向分量偏差小于2.5cm。在准动态对准动态的测试条件下，单历元解算结果精度较高，满足一些高动态精密定位指标要求。

b.动态对动态相对定位实验

实验过程中基准站保持静止，移动基站架设在事先设定的某点的天线支架上沿径向来回运动，动动差分实验的另一移动站固定在另外一点的小推车上，小推车沿着田径场跑道做往返几次运动。整个试验中测试时间为40min，共计1200个历元。在以移动基站为中心建立东北天（ENU）坐标系下，动动差分解算得到的相对位置矢量分量变化如图 4所示，依次为东向，北向以及天向的相对位置矢量变化。

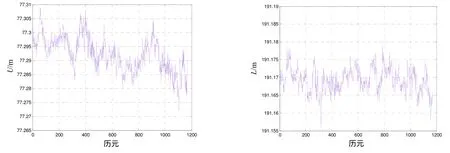
图4 东北天坐标系下相对位置矢量坐标及长度变化图

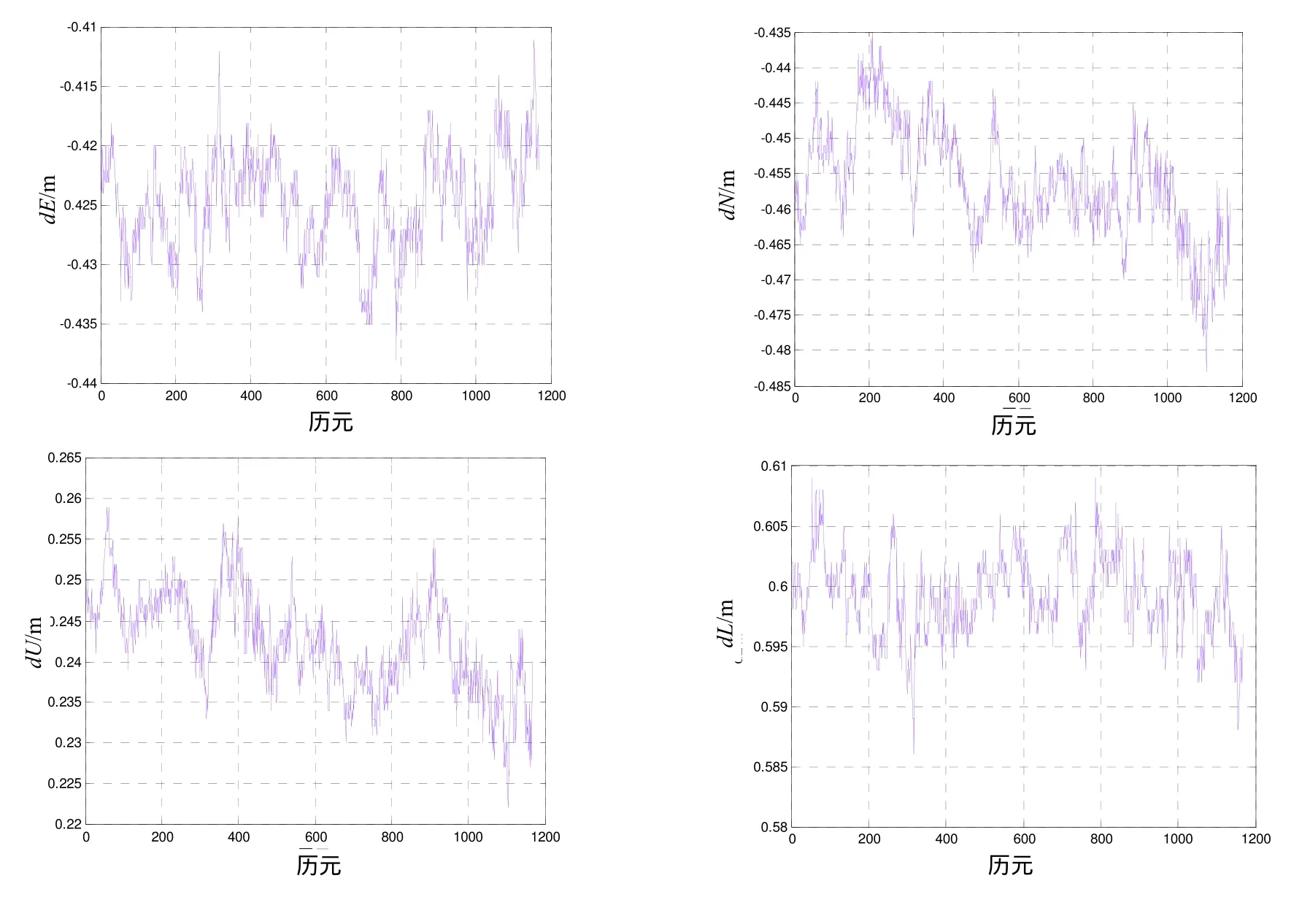
图5 东北天坐标系下相对位置矢量坐标和长度偏差

将上面计算结果与两组常规载波相位 RTK计算得到的标准值进行比较，偏差曲线如图5所示。

测试总长度为 1200个历元，由于测试数据较长，解算的数据具有一般性特征。可以清楚看到单历元相对位置矢量 E、N、U方向分量偏差均小于0.5m，表明在动态测试条件下，本算法对于解算单历元的结果能够满足一定的精度需求。

5 总结

本文从动动差分实现原理角度，建立了在动动相对定位条件下的定位模型，设计提出了准动态和动动测试两种试验方案。针对两种试验方案设计了试验平台，并进行了相应的试验验证。结果表明，在准动态测试方案中，测试基线的坐标分量和长度偏差小于2cm，在动动测试方案中，得到的东北天方向分量和基线长度偏差小于 50cm，验证了本文动动差分相对定位算法的精度性能。

[1]邱蕾,花向红,蔡华,等.GPS短基线整周模糊度的直接解法[J].武汉大学学报.信息科学版,2009（1）：97-99.

[2]李征航,黄劲松.GPS测量与数据处理[M].武汉大学出版社,2009.

[3]邢喆,王泽民,伍岳.利用模糊度聚类方法筛选GPS载波相位组合观测值[J].武汉大学学报.信息科学版,2006（1）：23-26.

[4]李卫军,姜卫平,王泽民.GPS载波相位三频组合观测值的模型研究[J].测绘信息与工程,2008（3）：6-8.

[5]李学逊.GPS载波相位观测值的线性组合及其相关性分析[J].测绘通报,1994（3）：10-15.

[6]刘超,王坚,路鑫,高井祥.GPS 载波相位观测值随机模型的比较研究[J].测绘科学,2010（6）：151-154.

[7]赵亮,叶世榕,陈德忠,刘炎炎.组合观测值确定L1&L2 的模糊度的探讨[J].测绘地理信息,2013（4）：36-38.

[8]Melbourne W.G(1985).The Case for Ranging in GPS-base Geodetic Systems.Rockville[M].Maryland:Proceeding of the First International Symposium on Precise Positioning with the Global Positioning System.

[9]Landau H,Euler H J.On-the-fly ambiguity resolution for precise differential positioning [J].Proceedings of GPS-92.Alexandria Virginia:The institute of navigation,1992:607-613.

[10]CHEN D.Fast ambiguity search filter(FASF):a novel concept for GPS ambiguity resolution[J].Proceedings of GPS-93.Alexandria,Virginia:The Institute of Navigation,1993:781-787.