具有逆断面的拟纯正半群的同余

王丽丽，闫　媛

(1.重庆理工大学 数学与统计学院，重庆　400054； 2.西北大学 数学学院，西安　710127)

具有逆断面的拟纯正半群的同余

王丽丽1，闫媛2

(1.重庆理工大学 数学与统计学院，重庆400054； 2.西北大学 数学学院，西安710127)

摘要:利用具有逆断面的拟纯正半群的分件半群L和R上的 o-同余所构成的同余对来构造此类半群的同余，证明了此类半群的所有o-同余的集合构成一个完备格。

关键词：拟纯正半群；逆断面；同余；完备格

1Introductions

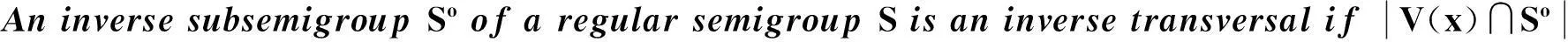
playaveryimportantroleininvestigatingthestructureS.In[3],McAlisterandMcFaddenshowedthat,ifSoisaQ-inversetransversalofS,thenΙandΛaresubbandsofS.TheregularsemigroupswithQ-inversetransversalSocanbeassembledbythreebricksSo, ΙandΛ,whereΙandΛareleftandrightnormalsubbandsofSrespectively(see[3]).

AregularsemigroupSiscalledquasi-orthodoxifthereexistaninversesemigroupTandasurjectivehomomorphismφ:S→Tsuchthattφ-1isacompletesimplesubsemigroupofSforeacht∈E(T),whereE(T)denotesthesetofidemopotentsofT.LetSbeaquasi-orthodoxsemigroupwithaninversetransversalSo.In[5],SaitoshowsthatI[Λ]isaleft[right]regularband.Let

Weobtainedin[5]and[11]thatL∩R=So, Ι∩Λ=E(So), E(L)=Ι, E(R)=ΛandthatΙ[Λ]isasubbandofSifandonlyifL[R]isasubsemigroupofS.Inthiscase, L[R]isaleft[right]inversesubsemigroupofS.

ThecongruenceonregularsemigroupswithinversetransversalswasstudiedbyWangandTang(see[8-10]).In[8],theauthorsassembledthecongruenceonSo.In[5],Satiogaveastructuretheoryofquasi-orthodoxsemigroupswithinversetransversals.Inthispaper,wegivetheo-congruenceonquasi-orthodoxsemigroupswithinversetransversalsbytheo-congruencepairandthestructuretheoryin[5]andprovethatthesetofallo-congruencesonthiskindofsemigroupsisacompletelattice.

2Preliminaries

Welistseveralknownresults,whichwillbeusedfrequentlywithoutspecialreferenceinthispaper.

Lemma2.1[2]LetSbearegularsemigroupwithaninversetransversalSo.Then： ① Ι={e∈E(S): eLeo}; ② Λ={f∈E(S): fRfo}.

Lemma2.2[8]Sisorthodoxifonlyifforanyx,y∈S,(xy)o=yoxo.

Lemma2.3[11]LetSbearegularseigroupwithaninversetransversalSo.

ThenR[L]isasubsemigroupofSifandonlyifI[Λ]isasubsemigroupofS.

Lemma2.4[5]LetLbealeftinversesemigroupandRarightinversesemigroup.SupposethatLandRhaveacommontranserversalSo.LetR×L→Ldescribedby(a,x)→a*xbemappingsuchthat,foranyx,y∈Landforanya,b∈R.

(Q.1) (aox)o=(a*x)o;

(Q.2) (aox)o(aox)=xoaoaooxooand

(a*x)(a*x)o=aooxooxoao;

(Q.3) aox xo(boy)=(aox)(aox)o((a*x)xoboy)and(a*x)xob*y=(a*xxo(boy))(b*y)o(b*y);

(Q.4) aoxo=aooxo,a*xo=axo,ao*x=aoxooandaoox=aox.

Defineamultiplicationontheset

by

ThenΓisaquasi-orthodoxsemigroupwithaninversetransversalwhichisisomorphictoSo.

Conversely,everyquasi-orthodoxsemigroupwithaninversetransversalcanbeconstructedinthismanner.

ForaregularsemigroupSwithaninversetransversalSo,thecompletelatticeofcongruencesonSisdenotedbyCon(S)andletρo=ρ|So.

3Themainresults

Inthissection,wefirstestablishacharacterizationofo-congruencesabstractlybyo-congruencespair.Wedescribeao-congruencespairoftheform(ρL,ρR)withρL∈Con(L)andρR∈Con(R)satisfyingsomeconditionsinorderthattheyproduceao-congruenceonSnaturally.

Definition3.1AcongruenceρofaregularsemigroupSwithaninversetransversalSoisao-congruence,ifforx,y∈S,xρyifandonlyifxoρoyo.

SupposeρRandρLareo-congruencesonRandL,respectively.Then(ρL,ρR)iscalledao-congruencepairforΓifthefollowingconditionshold:

(C.1) ρL|So=ρR|So;

(C.2) (∀c∈R)(∀x,y∈L)xρLy⟹(cox)ρL(coy) and (c*x)ρR(c*y);

(C.3) (∀z∈L)(∀a,b∈R)aρRb⟹(aoz)ρL(boz) and (a*z)ρR(b*z).

Define a relationρ(ρL,ρR) onΓby the following rule,

Theorem3.2LetΓbeaquasi-orthodoxsemigrouphavinganinversetransversalasinLemma2.4,and(ρL,ρR)beao-congruencepaironΓ.Thenρ(ρL,ρR)isao-congruenceonΓ.Conversely,everyo-congruencepaironΓcanbeconstructedintheabovemanner.

ProofLet(ρL,ρR)beao-congruencepaironΓ.Obviously, ρ(ρL,ρR)isanequivalenceonΓ.For(x,a),(y,b)∈Γ,with(x,a)ρ(ρL,ρR)(y,b),wehavexρLy,aρRb.Letz∈Landc∈Rbesuchthat(z,c)∈Γ.ByaρRbandC.3,wehave

Itfollowsthat

xxo(a oz)ρLyyo(b oz) and

(a*z)cocρR(b*z)coc

FromQ2,wehave

sothatzozoo(aoz)o=(aoz)o.Thus

Andsimilarly,

Hence,byQ1,wehave

Similarly,

Thus

Thatis,

Andwecanprovesimilarly,

Thusρ(ρL,ρR)isacongruenceonΓ.SinceρRandρLareo-congruenceonRandL,respectively.ThenwehavexoρL|S o yo,aoρR|S o bo.Itfollowsthat

Itisclearthat(x,a)o=(xo,ao)forany(x,a)∈Γ.Thereforeρ(ρL,ρR)isao-congruenceonΓ.

Conversely,assumethatρisao-congruenceonΓ.WedefinethefollowingequivalencesonLandR,respectively,

SinceρisacongruenceonΓ,wehaveρLandρRareequivalencesonLandR,respectively.

Let(x,a),(y,b),(x1,a1),(y1,b1)∈Γ.IfxρLyandx1ρLy1,then

Nowweimmediatelyget

Andthisimpliesthat

Then

Sowehaveprovedthatxx1ρLyy1.Similarly,wehaveaa1ρRbb1.

ItisobviousthatxρLyifandonlyifxoρLyoandaρRbifandonlyxoρRyo.ThereforeρL,ρRareo-congruence.

Andwehavethefollowingcases:

① ρR|So=ρL|Soisobvious.SoC.1holds.

②Letx,y∈LandxρLy.Then

Hence,forany(z,c)∈Γ,

Thatis,

Sinceρisao-congruenceonΓ,

ByQ1andQ2,

Itfollowsthat

(cox)oρL(coy)oand(c*x)oρR(c*y)o

SinceρL,ρRareo-congruence,

NowC.2holds.

③WecansimilarlyproveC,3.Nowfromtheaboveprove, (ρL,ρR)isao-congruencepaironΓ.

Bythedirectlypart, ρ(ρL,ρR)isao-congruence.If(x,a)ρ(ρL,ρR)(y,b),thenwehave

xρLy,aρRb

Thus

Itfollowsthat

Thatis

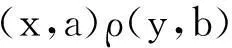
Thus, ρ(ρR,ρL)⊆ρ.Sinceρ⊆ρ(ρR,ρL)isobvious, ρ(ρR,ρL)=ρ.

Wedenotethesetofallo-congruencesonΓandthesetofallo-congruencepairsonΓconstructedasinTheorem3.2byC(Γ)andCP(Γ).

Thereverseimplicationisobvious.

Define≤onCP(Γ)by

ThenCP(Γ)isapartialorderedsetwithrespectto≤.ByTheorem3.2andLemma3.3,wecaneasilyseethatC(Γ)andCP(Γ)areisomorphicaspartialorderedset.

Proposition3.4LetΩ⊆C(T)andTρ=(ρL,ρR)whereρ∈Ω.Then

Thisimpliesthat

Wehaveprovethat

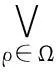
Now,bysumminguptheaboveresults,weobtainthefollowingtheorem.

Theorem3.5letΓbeconstructedinTheorem2.4.ThenCP(Γ)formsacompletelatticewithrespectto≤andC(Γ)isisomorphictoCP(Γ)ascompletelattice.

References:

[1]BlythTS,McFaddenRB.Regularsemigroupswithamultiplicativeinversetransversal[J].ProcRoySocEdinburgh, 1982, 92A: 253-270.

[2]TangXL.Regularsemigroupswithinversetransversal[J].SemigroupsForum, 1997, 55(1): 24-32.

[3]McAlisterDB,McFaddenRB.Regularsemigroupswithinversetransversals[J].QuartJMathOxford, 1983, 34(2): 459-474.

[4]McAlisterDB,McFaddenRB.Regularsemigroupswithinversetransversalasmatrixsemigroups[J].QuartJMathOxford, 1984, 35(2): 455-474.

[5]SatioT.Quasi-orthodoxsemigroupswithinversetransversals[J].SemigroupForum, 1987, 36:47-54.

[6]PetrichM.Thestructureofcompletelysemigroups[J].TransAmMathSoc, 1974, 189: 211-236.

[7]PetrichM,ReillyN.Completelyregularsemigroups[M].NewYork：Wiley, 1999.

[8]WangLM.OncongruencelatticeofregularsemigroupswithQ-inversetransversals[J].SemigroupForum, 1995, 50: 141-160.

[9]TangXL,WangLM.Congruencesonregularsemigroupswithinversetransversals[J].CommAlgebra, 1995, 23: 4157-4171.

[10]WangLM,TangXL.Congruencelatticeofregularsemigroupswithinversetransversals[J].Comm.Algebra, 1998, 26: 1234-1255.

[11]SaitoT.Anoteonregularsemigroupswithinversetransversals[J].SemigroupForum, 1986,33: 149-152.

(责任编辑刘舸)

收稿日期：2015-06-18

基金项目：西北大学研究生自主创新基金资助项目(YZZ14082)

作者简介：王丽丽(1982—)，女，山东泰安人，博士，主要从事代数学群论研究。

doi:10.3969/j.issn.1674-8425(z).2015.08.027

中图分类号：O175

文献标识码：A

文章编号：1674-8425(2015)08-0150-05

CongruencesonQuasi-OrthodoxSemigroupswithInverseTransversals

WANGLi-li1, YAN Yuan2

(1.CollegeofMathematicsandStatistics,ChongqingUniversityofTechnology,

Chongqing400054,China; 2.SchoolofMathematics,

NorthwestUniversity,Xi’an710127,China)

Abstract:We gave a o-congruence on a quasi-orthodox semigroups with inverse transversals Soby the o-congruence pair abstractly which consists of o-congruence on the structure component parts L and R. We proved that the set of all o-congruences on this kind of semigroups is a complete lattice.

Key words:quasi-orthodox semigroups; inverse transversal; congruence; complete lattice

引用格式：王丽丽，闫媛.具有逆断面的拟纯正半群的同余[J].重庆理工大学学报：自然科学版，2015(8):150-154.

Citationformat：WANGLi-li,YANYuan.CongruencesonQuasi-OrthodoxSemigroupswithInverseTransversals[J].JournalofChongqingUniversityofTechnology:NaturalScience，2015(8):150-154.