基于三轴气浮台的微波成像仪干扰力矩测量方法研究
翁艺航,杨立峰,薛孝补,刘鹏飞
(1.上海航天电子技术研究所,上海 201109;2.上海卫星工程研究所,上海 200240;3.上海交通大学 机械动力学院,上海 200240)
0 引言
FY-3气象卫星为我国第二代极轨气象卫星,配置的微波成像仪是主要遥感仪器之一。该载荷可实现全球降雨、云和大气中水汽含量、土壤湿度、海温、海冰、雪覆盖及海面油污等分布的探测。微波成像仪采用机械扫描方式,其转动部分质量60kg,转动周期分1.7,1.8,2.0s三档。以微波成像仪为代表的大型部件在装星前应进行干扰力矩的测量,对其静不平衡量、动不平衡量进行配平,减少其运转过程对卫星姿态的干扰。本文对一种基于三轴气浮台的微波成像仪干扰力矩测量方法进行了研究。
1 动力学模型
1.1 坐标系
气浮台坐标系:气浮台台体上标有刻度,取0°位置为OXt轴;90°位置为OYt轴;OZt轴与OXt、OYt轴右手正交。
成像仪坐标系:微波成像仪的机械零位(成像仪锁定位置)为成像仪坐标系OXc轴;OZc轴与台体OZt轴重合;OYt轴与OXt、OZt轴右手正交。
微波成像仪坐标系绕OZc轴以ω(1.7,2.0s两档)旋转,方向-OZc轴(俯视顺时针方向)。
微波成像仪坐标系OXc轴与气浮台坐标系OXt轴间夹角β=11.25°,两坐标系间关系如图1所示。
1.2 动平衡试验动力学模型
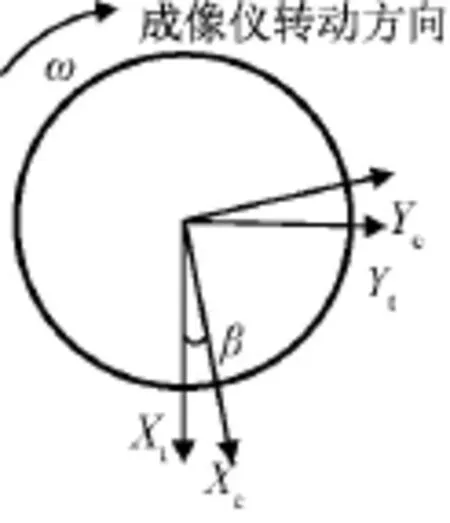
图1 微波成像仪坐标系与气浮台坐标系间关系Fig.1 Relationship of MWRI coordinate and air testbed coordinate
假设一圆柱旋转体绕其中心轴以ωw匀速旋转,原为一动不平衡转动体如图2所示。经动平衡测试后,在圆柱体上增加质量块(m1,r1),(m2,r2),(m3,r3)后,其整体会达到动平衡状态,m1,m2的连线过中心转动轴,且满足m1r1+m2r2=0。取转动体上的任意微元体dm,其至点A的矢径为r,点A在转动轴上。根据达朗贝尔原理有
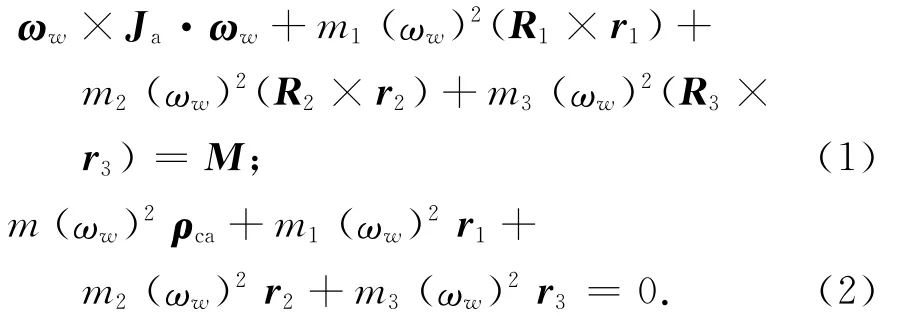
式中:Ja为圆柱旋转体相对质心c的转动惯量;M为外部施加在圆柱旋转体的力矩;m为圆柱旋转体质量;ρca为转动轴至转动体质心c的矢径[1-2]。
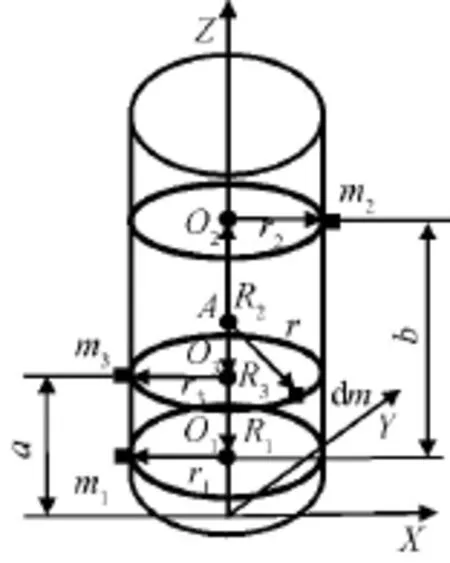
图2 三平面动平衡配平法Fig.2 Three plane dynamic balance
根据动平衡的条件及整个转动体处于匀速转动状态,有M=0。则式(1)、(2)可改写成
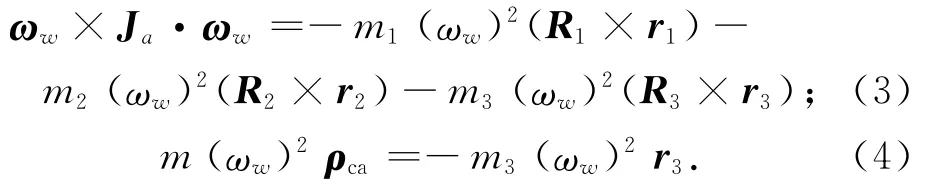
因点A在转动轴上是任意取定的,故可取点A的高度为a,则R3=0,式(3)可改写成
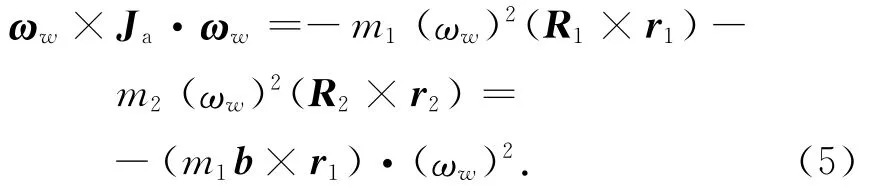
式中:b=R1-R2。此处:定义m1b×r1为偶不平衡量,m3r3为静不平衡量。
2 微波成像仪干扰力矩测量原理
2.1 静不平衡测量原理
静不平衡量测量时,气浮台不进行姿态控制,微波成像仪不转动,将其转动部分置于0°位置时,由姿态动力学及式(4)可知

式中:J为微波成像仪安装在台体后的转动惯量阵;ω1为陀螺测量的台体角速度;Md为气浮台干扰力矩;mpz为气浮台台体配重;rpz为台体配重位置矢量。因ω1较小,ω1×J×ω1可忽略不计,则式(6)简化为
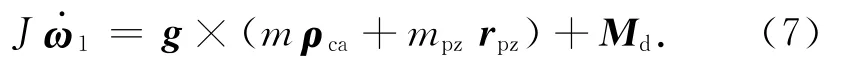
同理可得,微波成像仪180°位置时
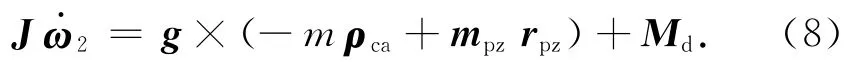
式(8)、(7)相减即可得mρca,进而求得微波成像仪的静不平衡量

2.2 偶不平衡测试原理
动不平衡量测量时,微波成像仪以ωw转动,在三轴气浮台姿态不控状态下,测量三轴气浮台输出的姿态角和角速度,由姿态动力学及式(4)可知

同样忽略ω1×J×ω1,将式(9)代入式(10)得
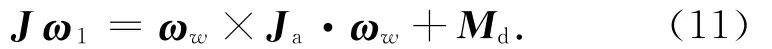
对试验获得的角速度信号进行频谱分析,分离出频率ωw=2π/Tw信号的幅值A和相位角δ。此处:Tw为成像仪转动周期。
分析气浮台X轴方向角速度信号,可得合力矩Mc=JxωwA。此处:Jx为气浮台X轴方向转动惯量。根据矢量合成原理求得偶不平衡力矩Md,偶不平衡量Cd=Md/(ωw)2。
3 测试数据分析
3.1 微波成像仪静不平衡测试数据分析
微波成像仪转动部分分别在零位与成像仪OX轴正负两向重合进行测试。根据陀螺测量角速度数据拟合出OX、OY轴角速度斜率。0°三次测量数据拟合结果如图3、4所示,求平均后得角速度斜率=1.223×10-4(°)/s,=-2.765×10-4(°)/s。180°三次测量数据拟合结果如图5、6所示,求平均后得 角 速 度 斜 率ω·2x=-2.362×10-2(°)/s,ω·1y=1.227×10-2(°)/s。
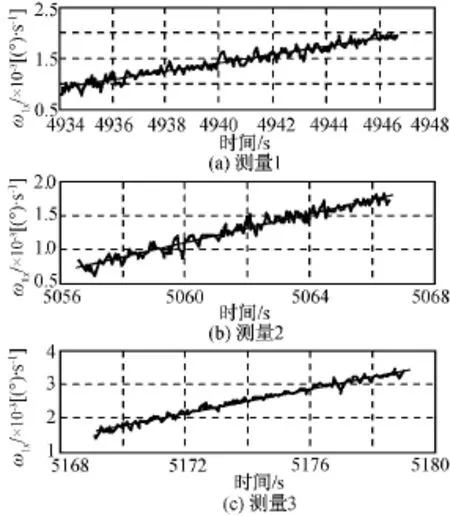
图3 0°X轴角速度曲线拟合Fig.3 Angular velocity of Xaxis at 0°
当气浮台X、Y轴转动惯量分别为Jx=2 478kg·m2,Jy=2 523.7kg·m2时,由角动量定理可算得不平衡力矩的X、Y轴分量分别为
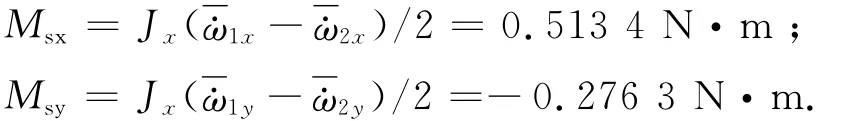
3.2 动不平衡测试数据分析
3.2.1 0.5Hz角速度信号提取
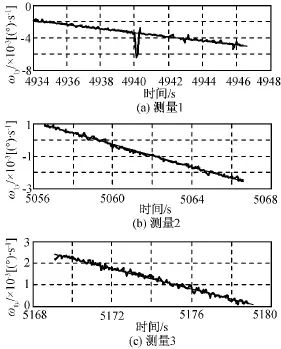
图4 0°Y轴角速度曲线拟合Fig.4 Angular velocity of Yaxis at 0°
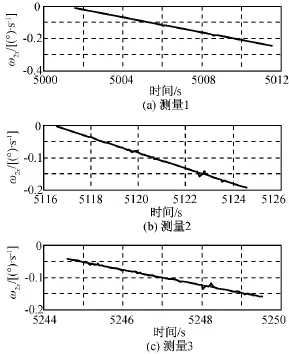
图5 180°X轴角速度曲线拟合Fig.5 Angular velocity of Xaxis at 180°
采样起始点7 582.1s(264),采样点数2 000,原始数据如图7所示。用Matlab软件作快速傅里叶变换(FFT)求解出原始数据的傅里叶变换[3]。求得0.5Hz角速度信号对应的复数-0.004 5+0.004 1j,其模值对应信号幅值的50%,幅角对应0.5Hz频率信号与cos(πt)的相位差,角速度信号的频谱如图8所示。则频率0.5Hz角速度信号的幅值为0.012 1 (°)/s,相位角为138.62°,即ωx=0.012 1×cos(πt+138.62)。
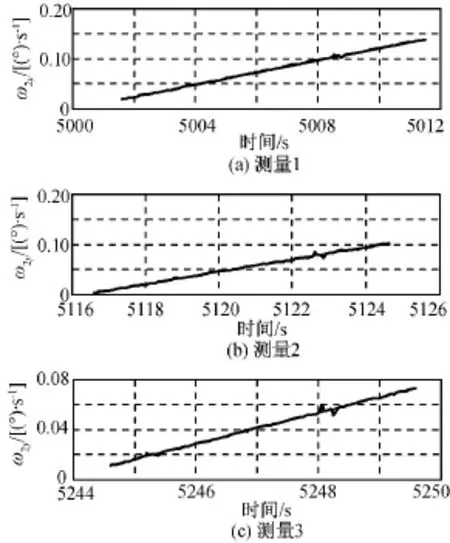
图6 180°Y轴角速度曲线拟合Fig.6 Angular velocity of Yaxis at 180°

图7 角速度原始数据Fig.7 Original data of angular velocity
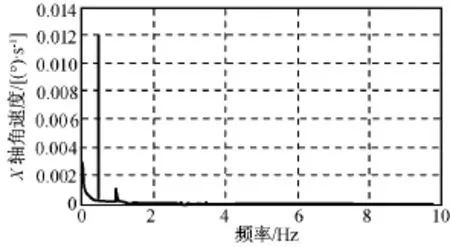
图8 角速度幅值频谱Fig.8 FFT of angular velocity
3.2.2 合力矩计算
由角速度信号幅值A可得合力矩Mc=JxωwA,相位超前角速度信号90°。
3.2.3 零位脉冲相位标定
因微波成像仪提供的零位脉冲在成像仪坐标系中的相位未知,且陀螺测量存在一定的相位滞后,为提高测量精度,需标定零位脉冲相对气浮台坐标系的相位。
在微波成像仪上安装一已知质量块,以脉冲时刻为时间零基准,分析数据得到配重产生的干扰力矩相位,与配重理论产生的干扰力矩相位相比较就可得脉冲相位。
取配重安装位置距离转动中心r=0.198m,质量m=180g,状态如图7所示。设OXc轴转动至图9中块位置时零位脉冲产生,其相对台体坐标系OXt轴角度为α。
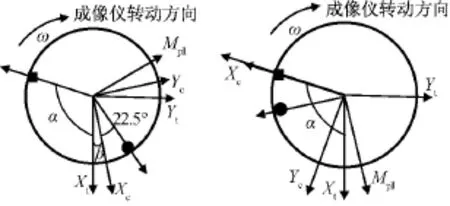
图9 标定配重位置Fig.9 Angle of demarcate bob-weight
以上述微波成像仪位置所在时刻为状态1,则微波成像仪以角速度ω(π)转动时配重块产生的力矩Mpll(重力力矩和离心力力矩)在气浮台体坐标系OXt轴分量
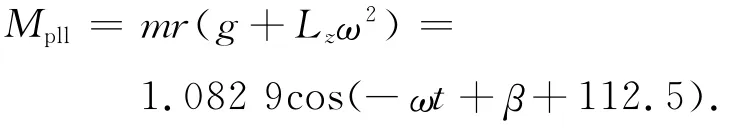
式中:Lz为配重在气浮台坐标系位置Z向分量。
当微波成像仪旋转α+β后,此时微波成像仪OXc轴转到脉冲发生位置处,微波成像仪输出零位脉冲,相对位置关系如图10所示,记此时刻为状态2,则以状态2为时间零基准,微波成像仪以角速度ω(π)转动时配重块产生的力矩Mpll(重力力矩和离心力力矩)在台体坐标系OXt分量为
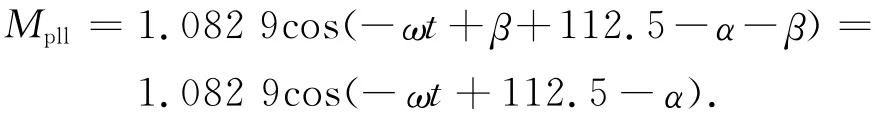
根据实验数据无配重时的干扰力矩和增加配重后的干扰力矩可得零位脉冲产生时刻(t0)为起始配重产生的干扰力矩
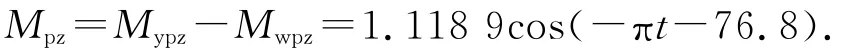
以脉冲产生时刻为零位时间基准,比较配重理论值与实际测量值得α=189.3°。
3.2.4 偶不平衡力矩计算
无配重时零位脉冲产生时刻即t0时刻,则可知此时FFT算得的成像仪干扰力矩产生的角速度信号为ωx=0.012 1cos(-πt-138.6)。
力矩信号超前角速度信号90°相位,Mwpz=1.644cos(-πt+131.4°)。
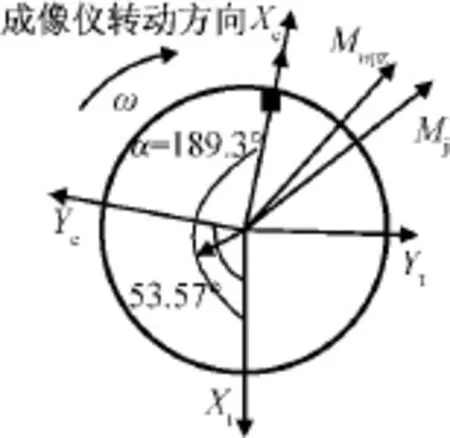
图10 零位脉冲、合成力矩和静不平衡力矩间位置关系Fig.10 Phase position relationship
以上述计算得到的微波成像仪旋转时以脉冲时刻为时间基准零位,静不平衡力矩在台体坐标系OXt方向的分量
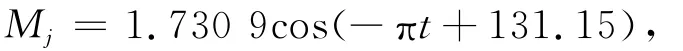
偶不平衡力矩为

则可知偶不平衡力矩为0.087 2N·m,偶不平衡量为8 863.3kg·mm2,在成像仪坐标系中相位为135.73°。
3.3 气浮台测试精度验证
对气浮台精度进行验证。在气浮台已调平条件下,在微波成像仪转动部分分别增加一定质量的配重,其在微波成像仪坐标系中位置为:相位112.5°,距离转动中0.204m,质量25g,距圆盘高度6mm。理论值与实测值分别见表1、2。由计算可知:气浮台静不平衡、偶不平衡力矩的测试精度优于0.01N·m,满足0.03N·m的使用要求。
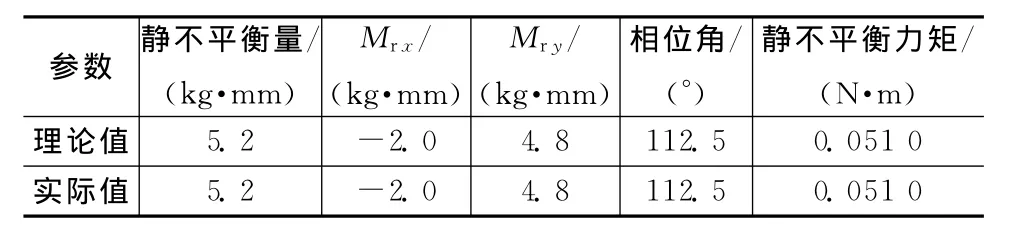
表1 静不平衡力矩测试精度验证Tab.1 Static balance precision validation
根据本文分析结果,对微波成像仪进行配平,其转动产生的干扰力矩显著减小,卫星控制精度大幅提高,卫星姿态三轴控制精度如图11所示,可达0.1°。微波成像仪开机后卫星姿态三轴控制精度如图12所示。微波成像仪工作正常、性能稳定、图像质量良好,在轨动不平衡得到了有效解决。
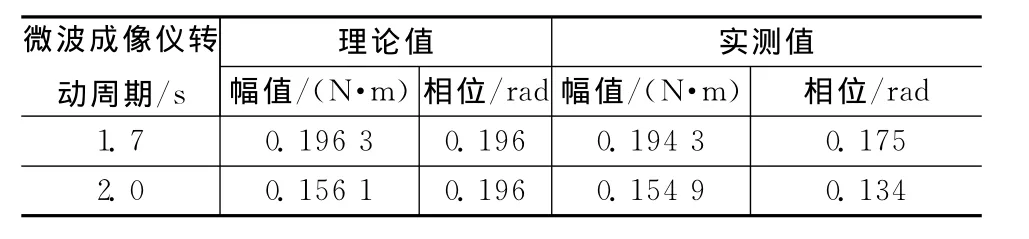
表2 偶不平衡力矩测试精度验证Tab.2 Dynamic balance precision validation
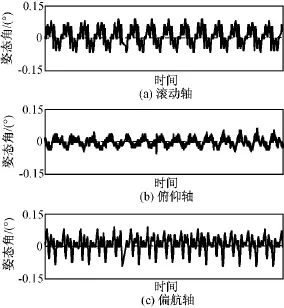
图11 微波成像仪开机前卫星三轴控制精度Fig.11 Three-axis control-precision of satellite for MWRI not working
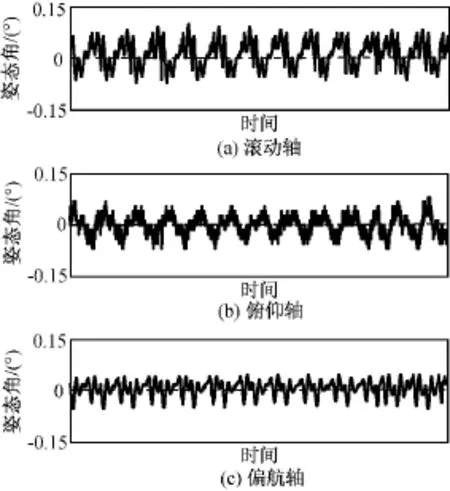
图12 微波成像仪开机后卫星三轴控制精度Fig.12 Three-axis control-precision of satellite for MWRI working

表5 算法单次检测概率Tab.5 Single detection probability of algorithm
4 结束语
针对高灵敏度深空应答机载波捕获的性能需求,本文研究了一种快速解线调载波捕获算法。经仿真和FPGA板级验证表明,该算法可准确捕获归一化信噪比为25dBHz、多普勒频移-300~+300kHz、多普勒一次变化率-3~+3kHz/s的信号。给出了工程应用的应用模式和参数设置,计算了其资源占用、运算时延与单次检测概率。在信噪比低至21.235dB时,算法的单次检测概率高于94.97%。
[1] 陈昌亚.浅谈奔赴火星需要解决的几大关键技术[J].自然杂志,2012,34(2):83-87.
[2] 薛文虎,张明敏,唐劲松,等.Chirp信号参数估计算法性能比较[J].海军工程大学学报,2007,19(2):1-5.
[3] 朱春华,穆晓敏.Chirp信号三种检测方法的性能分析[J].雷达科学与技术,2008,8(1):39-43.
[4] 吴长奇,田 园,韩秀峰.极低信噪比大多普勒频移条件下基于双谱实现载频提取[J].电子技术,2009(8):75-77.
[5] 韩孟飞,崔 嵬,王永庆,等.极低载噪比高动态信号的捕获策略研究与仿真[J].系统仿真学报,2009,21(23):7589-7592.
[6] 常 龙,姜秋喜,潘继飞.宽带线性调频雷达信号特征研究[J].中国雷达,2008(1):44-46+56.
[7] 闫红蕊.高分辨率SAR图像中车辆目标的检测[D].郑州:中原工学院,2009.
[8] GANDHI P P,KASSAM S A.Analysis of CFAR processors in nonhomogeneous background[J].IEEE Trans on AES,1988,24(4):427-445.

