一种高灵敏度深空应答机载波捕获算法

方 轶，高 磊，王 灵，陈之纯

（1.上海航天电子技术研究所，上海 201109；2.上海航天技术研究院，上海 201109）

0 引言

深空通信距离远，信号损耗大，噪声和干扰多，导致信号信噪比极低。如火星探测，由于地球与火星最近相距约5.6×107km，最远相距约4×108km，空间信号衰减可达280dB［1］。要求深空应答机须具备高灵敏度。为到达预定轨道，深空探测器与地面站的最大相对速度高，达到第二宇宙速度（脱离地球引力），致使信号载波的多普勒动态范围特别大。当信号信噪比极低时，通过延长相干积累时间可改善信噪比；若同时多普勒频移一次变化率较高，在长相干积累时间内的多普勒频移会很大，由此导致相干积累能量分散，无法捕获载波。

常用的基于线性调频（LFM）信号频率估计方法有 Wigner-Ville分布、Radon-Wigner变换、相位展开法、最大似然估计法等。文献［2-3］对这些常用的LFM信号频率估计方法进行了分析，但在极低的信噪比条件下，上述方法难以达到预期效果［4］。文献［5］提出了一种新的LFM信号估计算法，计算简单，可用于工程实现。在此基础上，本文对一种用于深空应答机载波环的快速解线调载波捕获算法进行了研究。

1 算法分析

1.1 基本原理

参考深空探测需求，本文重点考虑的待测信号指标为：最低归一化信噪比25dBHz（对应应答机灵敏度－147dBm）；载波多普勒频移范围－300～＋300kHz；载波多普勒频移一次变化率范围－3～＋3kHz／s。其中，后两项指标合称为载波多普勒动态范围。

深空探测采用统一载波测控体制，遥控信号和侧音信号按相位调制（PM）的方式调制在载波上。为便于研究，取载波信号幅值为1，测距音仅考虑主侧音，载波初始相位和遥控副载波初始相位均为0。在足够短的时间段内，可认为多普勒频移二次变化率为零，即信号载波的多普勒频移随时间呈线性变化。这样，待测信号就简化为LFM信号，待测信号的实际载频（含多普勒频移）和多普勒频移一次变化率可等同于LFM信号的初始频率和调频斜率。由此，待测信号可表示为

式中：fc0为实际载频（含多普勒频移），即LFM信号的初始频率；kc为多普勒频移一次变化率，即LFM信号的调频斜率；mj为侧音信号调制指数；sce（t）为侧音信号；m为遥控副载波调制指数；stlc（t）为遥控副载波信号。

快速解线调载波捕获算法的信号流程如图1所示。为减少中频处理的数据量，先将待测信号数字下变频至500kHz。数字下变频后的信号载频（含多普勒频移）范围为＋200～＋800kHz，采样率降为3MHz。因此，图1中的中频数字输入信号可表示为

式中：θ（n）＝mjsce（n）＋mstlc（n）；n＝k／（3×106），整数k∈［0，3×106T］。此处：T为信号持续时间。

图1 算法信号流程Fig.1 Signal flowchart of algorithm

若用于正交下变频的本地信号频率为fL，则经正交下变频后的信号为

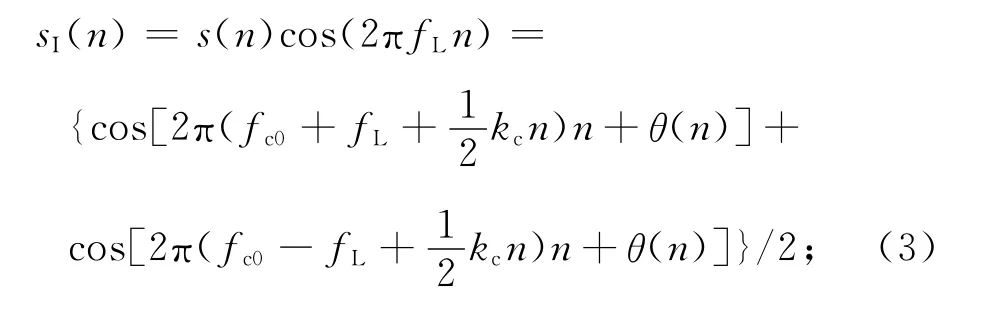
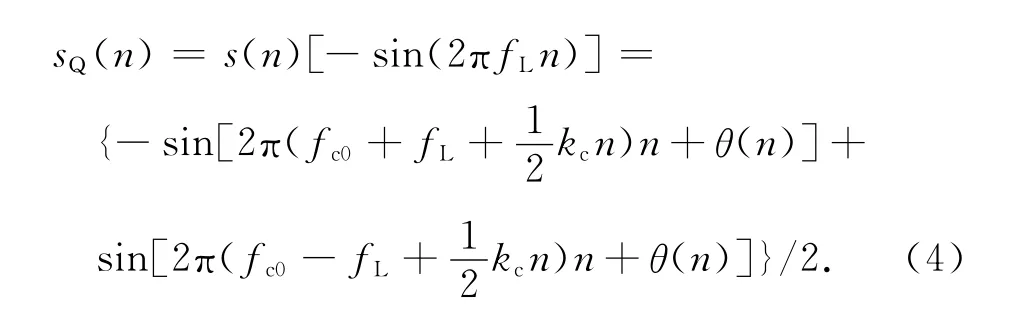
再经二次采样后的I、Q两路信号分别为

式中：m＝k／fss；整数k∈［0，fssT］。此处：fss为二次采样频率。

若用于对消的本地预置值为kL，则经对消后的I、Q两路信号分别为

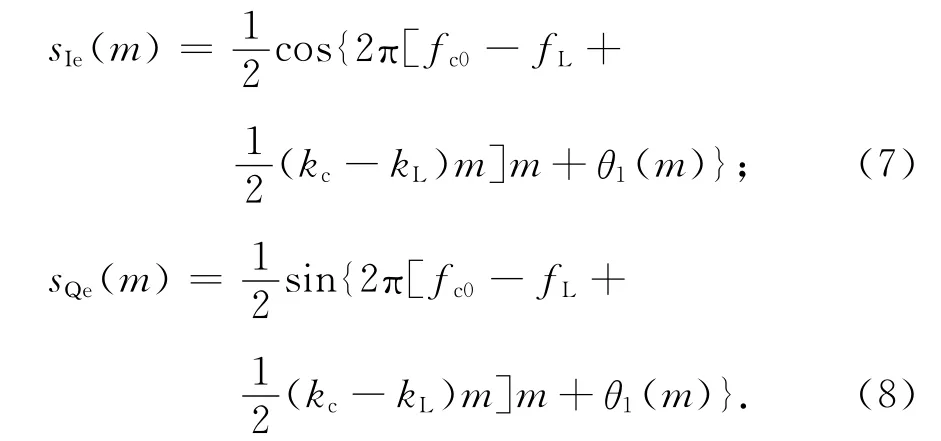
由式（7）、（8）可见，对消后的I、Q 两路信号仍为LFM信号，具有LFM信号的特性。

由Parseval定理可知：信号在时域的总能量与在频域的总能量相等，经傅里叶变换后信号的总能量保持不变，这符合能量守恒定理。因此，若设LFM信号s（t）的频谱为S（ω），则该信号的能量

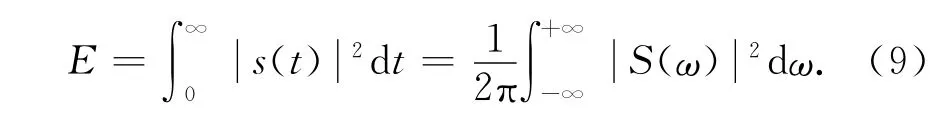
如文献［6］所述，LFM信号具近似矩形的幅频特性，且其时宽带宽积越大，菲涅耳纹波越小，幅值频谱越接近于矩形，频谱宽度越近似等于信号带宽B。因此，当时宽带宽积远大于1时，可对式（9）作近似处理。将频域积分的区间换成0～B，并将S（ω）用定值代替，则

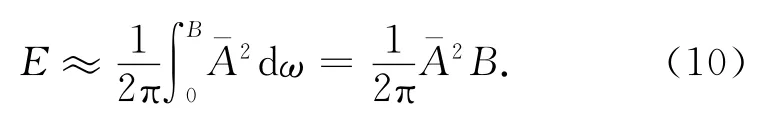
式中：为信号频谱幅值的均值。

已知，LFM 信号的B，kc，T满足关系式B＝kcT，将其代入式（10）可得

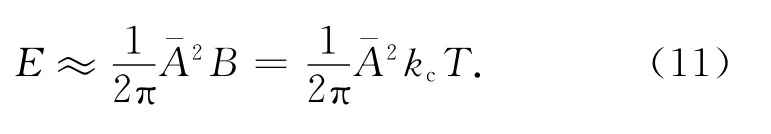
可见，LFM信号能量一定时，在相同持续时间内，信号频谱幅值平方与调频斜率成反比。式（7）、（8）中：kL与kc越接近，｜kc－kL｜值越小，对消后信号的多普勒频移一次变化率（调频斜率）越小，相应输出信号的频谱峰值就越高。这样，通过搜索频谱峰值，就可得到信号载波频率（初始频率）和多普勒频移一次变化率（调频斜率）的估值。

1.2 检测原理

该算法输入信号所夹杂的噪声是随机的，其变化会引起捕获概率的变化，因此需对算法的运算结果采用自适应恒虚警检测。信号恒虚警率（CFAR）检测，就是在干扰强度变化的情况下，信号经恒虚警率处理，使虚警概率保持恒定。CFAR处理中，确定自适应的平均判决门限（ADT）是关键。

假设噪声分布模型的概率密度函数为p（x），则求解

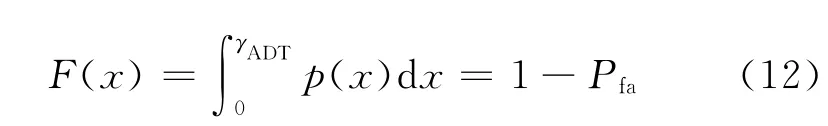
可得平均判决门限γADT［7］。此处：Pfa为虚警概率。

可用二分法在给定Pfa的条件下，得到式（12）的解γADT，即寻找一个正整数，满足

式（12）、（13）给出了自适应判决门限的一般求解方法。对不同的噪声背景，需用不同的CFAR检测方法。γADT通常表示为

式中：Ns为信号采样点数；Z为归一化判决门限。

对不同的噪声分布模型，CFAR检测的主要区别是Z的求取方法不同。假设信号噪声为高斯分布，则有

由Z可得单次检测概率

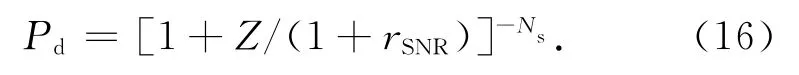
式中：rSNR为信号信噪比［8］。

由式（14）、（15）可得自适应判决门限

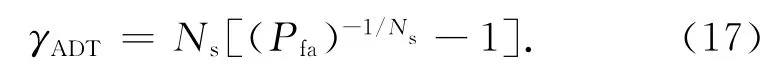
由式（14）、（16）可得单次检测概率

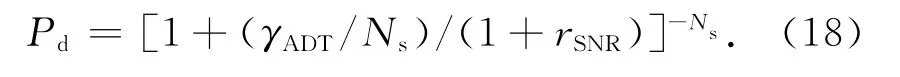
2 算法实现方案

根据算法原理设计实现方案，框图如图2所示。算法采用并行搜索方案，将输入的数字中频信号分成N路分别送至N个通道处理模块。每个通道处理模块除本地预置频率不同外，其余处理过程均相同。

图2 算法实现方案框图Fig.2 Block diagram of algorithm

因待测信号为PM调制信号，频谱并非单一谱线，单纯用低通滤波滤除带外噪声会造成信号频谱的混叠，故将正交下变频后的信号依次通过积分梳状（CIC）滤波器、半带（HB）滤波器和低通FIR滤波器。这样不仅可获得良好的滤波效果，而且能降低采样率，减小运算量。

降采样率后的信号仍是LFM信号，其初始频率为待测信号实际频率与本地预置频率的差，调频斜率仍为信号的多普勒频移一次变化率。将载波多普勒频移一次变化率的范围按固定步进划分为一组可能值。分别用这组可能值对待测信号的相位变化率进行对消，并对对消后的信号作快速傅里叶变换（FFT），可得一组FFT峰值及其对应的一组频点。对该组FFT峰值进行通道内比较选大，选出其中的最大值。该最大值对应的多普勒频移一次变化率可能值就是调频斜率的估值，对应的频点即为初始频率的估值。

获得初始频率和调频斜率的估值后，将初始频率估计值加上该通道的本地预置频率即是待测信号的实际载频估值，而调频斜率的估值则是待测信号的多普勒频移一次变化率估值。将这两个估值连同该通道内的最大FFT峰值及该峰值对应的峰均比作为该通道的输出，送至通道间模值比较选大模块。

通道间模值比较选大模块将各通道送来的最大FFT峰值再进行比较选大，选出其中的最大值，该最大值对应的通道即为正确通道。正确通道输出的载频和多普勒频移一次变化率的估值即为算法的捕获值。最后由判决模块完成是否成功捕获的判决。判决模块的判决量是正确通道输出的峰均比，判决门限采用恒虚警检测的方法设置。若正确通道输出的峰均比高于判决门限，则表明捕获成功；否则捕获失败，需重新捕获。

3 仿真与实现

3.1 Matlab仿真

在Matlab R2008a软件中对算法进行仿真验证。仿真参数为：待测信号载频263.872kHz；待测信号多普勒频移一次变化率2 781Hz／s；待测信号归一化信噪比25dBHz；待测信号采样频率3MHz；相干累积时长1.3s；下变频通道的中心频率划分步进20kHz；总通道30个；对消组的本地预置值划分步进4Hz／s；总组1 500个；二次采样频率25kHz。对式（2）的待测信号，加噪25dBHz后进行载波捕获，算法各通道中输出的FFT峰值分布如图3所示。

由图3可知：在通道本地预置值270kHz和对消组本地预置值2 782kHz／s的交汇处，z轴出现一个峰值，充分证明快速解线调捕获算法的理论正确。

仿真结果为：载频捕获值263 870.738 853Hz；载频捕获误差－1.261 147Hz；多普勒频移一次变化率捕获值2 782Hz／s；多普勒频移一次变化率捕获误差1Hz／s；峰均比21.235 008dB。可见，在归一化信噪比25dBHz的信号条件下，算法能正确捕获载波多普勒动态范围大的载波。

图3 算法仿真结果Fig.3 Matlab simulation result of algorithm

3.2 FPGA实现

在ISE中调用Modelsim软件，对算法中的变化率对消模块进行行为仿真，待测信号的参数设置如上。加噪25dBHz后，正确组对消后的仿真结果如图4所示。

图4的峰值处放大如图5所示。图中：有输出端口3个，dv（data valid）输出为高电平时，FFT输出数据有效；xk＿index为FFT输出数据的索引；sum为仿真输出的信号频谱。图4中标注的峰值是sum输出数据有效段（dv输出为高电平时）的最大值。

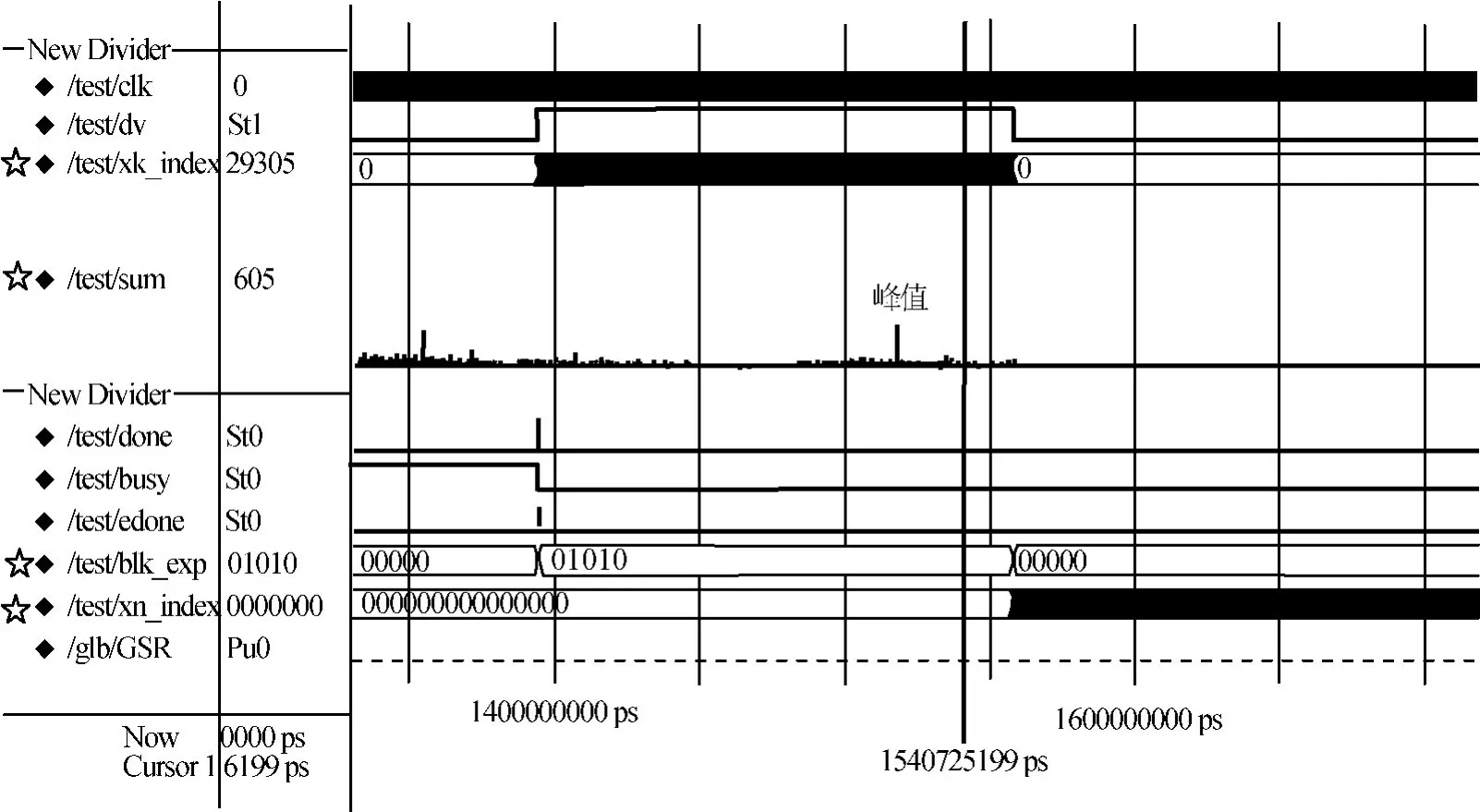
图4 关键模块ModelSim仿真结果Fig.4 ModelSim simulation result of key module

图5中，sum峰值对应的xk＿index为24 738。xk＿index减去由后续乘法器和加法器造成的延时后，得到sum峰值对应的输出索引为24 734。由sum峰值的输出索引24 734，信号的二次采样率25kHz和FFT点数215可计算出sum峰值对应的频点为－6 129Hz。sum峰值对应的频点加上该正交下变频通道本地预置值270kHz，得到载频捕获值为263.871kHz，与实际载波频率263.872kHz相差1Hz，捕获正确，误差在可接受范围内。

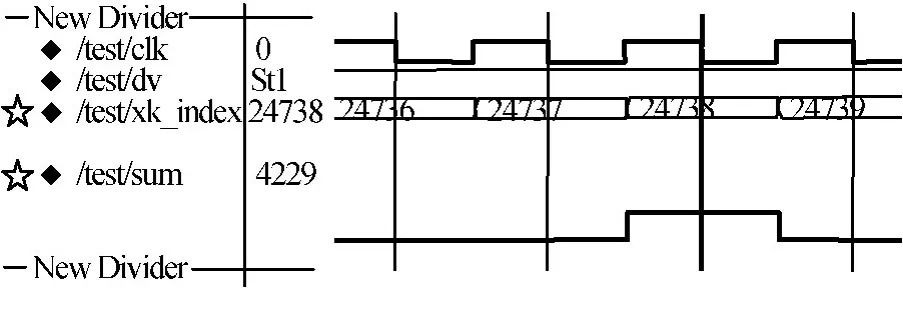
图5 关键模块的ModelSim仿真结果（放大）Fig.5 ModelSim simulation result of key module（zoom in）

算法板级验证的硬件平台采用XILINX公司的FPGA开发板ML605，板上FPGA采用XC6VLX240T-1FFG1156芯片，与 ML605配套使用的模数转换器评估板采用TI公司的ADS58C48EVM，两 者 用 适 配 卡 FMC-ADC-ADAPTER连接。

在上述硬件平台上对算法的变化率对消模块进行板级验证。通过片上逻辑分析仪（ChipScope Pro）对FPGA进行在线片内信号分析，加噪25dBHz时正确组对消后信号的频谱如图6所示。图6中：信号频谱峰值对应的输出索引为24 738，计算可得载频捕获值为263.871kHz，误差1Hz，捕获正确，误差在可接受范围内。

3.3 应用分析

在深空探测器飞向目标星球过程中，信号信噪比极低和载波多普勒动态范围极大两种极限情况不会同时出现。此外，在有先验经验的条件下，算法的搜索范围可大幅缩小，这就显著节省了搜索时间和硬件资源。为在不同条件下实现算法硬件资源和运算时间的优化，需根据CCSDS对深空信号指标的规定，对算法设置不同的工作模式。

本文对快速解线调载波捕获算法设置了4种工作模式，模式间的自动切换由载波环的锁定指示输出S1和射频前端模拟自动增益控制（AGC）的输出S2共同决定。不同切换条件对应的工作模式见表1。不同工作模式下，算法的参数设置、占用资源、时延和捕获判决门限的设置均不同。

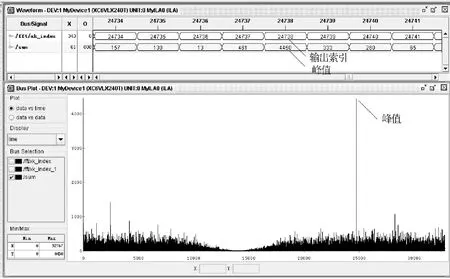
图6 关键模块硬件电路在线信号分析结果Fig.6 ChipScope simulation result of key module

表1 工作模式的切换条件Tab.1 Switching conditions in different operating modes

为实现资源和时间的优化，不同工作模式下算法的参数设置不同，见表2。

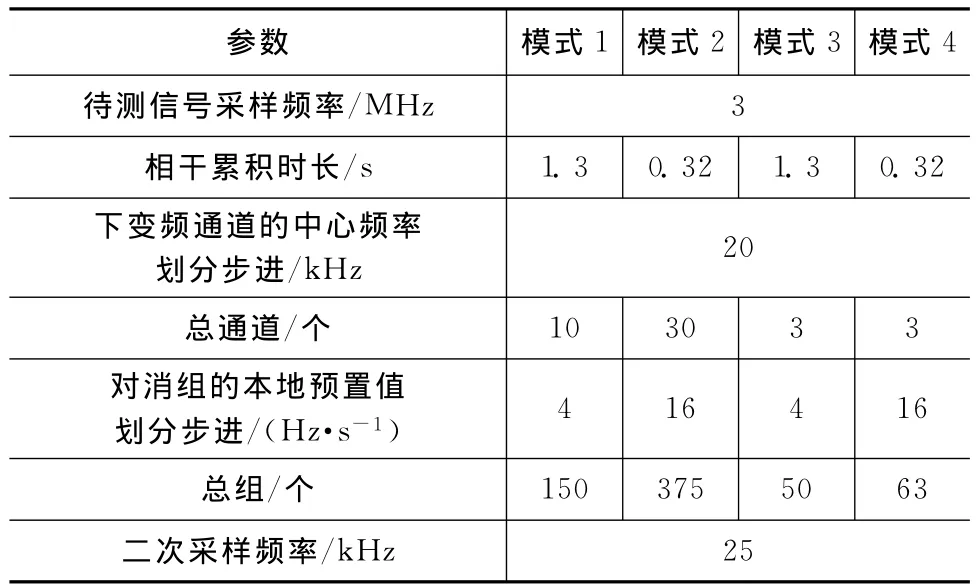
表2 不同工作模式算法参数Tab.2 Parameters of the algorithm in different operating modes

算法硬件采用的FPGA芯片为XILINX公司的 Virtex-6 240T（XC6VLX240T-1FFG1156）。每片240T含有：Slices 37 680个（含LUTs 4个和触发器8个），DSP48E1Slices 768个（含乘法器25×18个，加法器1个和累加器1个），18Kb Block RAMs 832个。

算法中，FFT相干积累模块运算量最大，占用资源达50%以上。因此，对算法的硬件资源占用量和捕获时间的分析主要针对FFT相干积累模块，结果见表3。表中的FFT点数取决于二次采样频率fss和相干积累时长T。

以采用Radix-2结构实现FFT，FFT输入／输出数据位数为8位，系统时钟200MHz为前提，用ISE12.2的 Resource Estimates估计出 FFT IP CORE占用的资源，用Latency可估计单次FFT运算的时延。结合单片240T的硬件资源可算出最大单次并行运算FFT的个数（以FFT占用总资源的50%计）。

在表3的基础上可得捕获算法在不同载波环工作模式下由运算产生的时延见表4。表中：FFT运算总个数为算法的总通道数N与总组数M之积；FFT运算总个数除以最大单次并行运算FFT个数可得串行FFT运算次数；FFT运算时延取决于串行FFT运算次数和单次FFT运算的时延；捕获算法总时延为FFT运算时延与数据缓存时延之和。由表4可知：载波环在不同工作模式下，由捕获算法运算产生总时延（含数据缓存时延）的极限值小于1.5s，而一般情况下，算法总时延（含数据缓存时延）小于0.5s。可见，算法的捕获时间在工程实现可接受的范围内。

设定虚警概率，由式（17）、（18）可得算法的单次检测概率，计算结果见表5。由表可知：即使在低信噪比工作模式下，算法的单次检测概率仍高于94.97%。

表3 单次FFT占用资源和运算时延Tab.3 Cost of hardware resource and time delay of single FFT operation

表4 不同工作模式下算法总时延Tab.4 Total time delay of algorithm in different operating modes

表5 算法单次检测概率Tab.5 Single detection probability of algorithm

4 结束语

针对高灵敏度深空应答机载波捕获的性能需求，本文研究了一种快速解线调载波捕获算法。经仿真和FPGA板级验证表明，该算法可准确捕获归一化信噪比为25dBHz、多普勒频移－300～＋300kHz、多普勒一次变化率－3～＋3kHz／s的信号。给出了工程应用的应用模式和参数设置，计算了其资源占用、运算时延与单次检测概率。在信噪比低至21.235dB时，算法的单次检测概率高于94.97%。

［1］ 陈昌亚.浅谈奔赴火星需要解决的几大关键技术［J］.自然杂志，2012，34（2）：83-87.

［2］ 薛文虎，张明敏，唐劲松，等.Chirp信号参数估计算法性能比较［J］.海军工程大学学报，2007，19（2）：1-5.

［3］ 朱春华，穆晓敏.Chirp信号三种检测方法的性能分析［J］.雷达科学与技术，2008，8（1）：39-43.

［4］ 吴长奇，田 园，韩秀峰.极低信噪比大多普勒频移条件下基于双谱实现载频提取［J］.电子技术，2009（8）：75-77.

［5］ 韩孟飞，崔 嵬，王永庆，等.极低载噪比高动态信号的捕获策略研究与仿真［J］.系统仿真学报，2009，21（23）：7589-7592.

［6］ 常 龙，姜秋喜，潘继飞.宽带线性调频雷达信号特征研究［J］.中国雷达，2008（1）：44-46＋56.

［7］ 闫红蕊.高分辨率SAR图像中车辆目标的检测［D］.郑州：中原工学院，2009.

［8］ GANDHI P P，KASSAM S A.Analysis of CFAR processors in nonhomogeneous background［J］.IEEE Trans on AES，1988，24（4）：427-445.