外弹道测量数据快速融合方法

段秀云,黄　瑜

(91550部队94分队，辽宁 大连　116023)

外弹道测量数据快速融合方法

段秀云,黄瑜

(91550部队94分队，辽宁 大连116023)

摘要：快速、精确融合计算弹道结果是试验过程中重要的基础工作之一，针对理论弹道失去参照作用，没有高精度测量设备参与的情况，提出了基于神经网络的快速弹道融合方法；首先，根据测量精度设定融合权值，然后剔除测量数据中异常测量误差并基于小波分析和频带分析分离随机误差，最后利用神经网络快速融合得到精度较高的弹道结果，同时还可以对参与融合测量数据的系统误差进行估计；通过实测数据的计算，验证了本文提出方法的可靠性和精度。

关键词：快速融合；融合权值；异常测量误差；神经网络

目前，弹道数据融合计算方法主要基于与理论弹道或者初始弹道的反复比对分析，以及借助高精度测量设备作为融合基准。随着多目标、高机动性高超声速导弹的出现，理论弹道与初始弹道的参照作用失去了意义。同时，在没有更高精度测量设备情况下的外弹道数据快速融合方法是一个有意义和亟需解决的研究内容之一。

现有数据融合算法主要基于相应的误差模型[1-5]，借助样条函数等方法分离误差再进行融合[6]；有的研究成果只对存在两种测量体制或测量设备的情况下进行融合计算分析[7-8]。由于需要建立精确的误差模型和估算众多模型参数，需要较长的运算时间，一般不适合快速处理应用。本文首先基于测量设备的精度建立相应的权重矩阵，剔除参与融合计算测量数据的异常信息并对有用的特征信息进行提取，然后借助神经网络实现测量数据的快速融合解算。通过对实测数据的计算，证明该方法能够快速，准确计算出精度较高的弹道结果，并可以对参与融合的数据误差进行估计。

1测量数据融合计算准备

1) 测量数据融合权重设定。由于测量体制与精度的差异，不同测量设备以及同种测量设备在不同测量站点测量得到的测量数据的误差都不相同。理论上，测量精度越高，测量误差越小，在进行融合计算时该数据的权重应越大。为了简化计算过程，本文就以设备的测量精度取对数归一化后作为测量数据进行融合计算的权重。实际计算过程中，还可以建立相应的测量设备测量精度评价指标体系，综合考虑测量精度、稳定性、使用年限、维护保养情况以及历次试验测量情况统计等方面，对设备的测量能力进行横向以及纵向综合评价，从而确定更准确的融合权重数值。这也是本文下一步即将开展的工作之一。

2) 测量数据异常信息的剔除。由于测量环境和测量条件的变化，测量数据在某些时间段落会出现测量异常误差，如果不进行判别并剔除，将会对融合结果产生很大影响。本文对测量异常误差的判别主要基于测量精度的顺序一致性来实现，即精度高的测量设备的测量误差不应比精度低的测量设备的测量误差大。如图1所示，正常情况下，精度高的测量设备B的测量数据应该比精度低的测量设备A更接近真值，阴影所示的测量数据就存在测量异常误差。

图1　异常测量误差示意图

剔除测量异常误差的具体过程：首先，根据现有数据融合计算初步融合弹道结果，按照测量精度最低测元的浮动范围为基准，粗略估算出融合弹道的误差允许范围，然后计算各测量数据的误差范围，如果某一测元数据的某段测量误差与融合弹道范围无交集，则可判断该段测量数据具有测量异常误差，需要在融合计算之前将其剔除。

3) 测元数据随机误差分离。测量数据一般由真值、系统误差和随机误差组成。系统误差借助权重分配通过多测元融合计算加以剔除，也是本文融合方法所要解决的主要问题。另外，为了提高计算精度，还需要抑制测量数据中的随机误差的影响，本文采用小波分解和频带特性结合对随机误差进行分离[9]，具体分离方法限于篇幅，不再赘述。

2测量数据快速融合计算与分析

精确的事后数据融合算法在建立精确误差模型的基础上，利用样条拟合、非线性拟合以及模糊聚类等算法，反复对参与融合的数据进行融合和比对，以达到融合残差或者方差最小。一般此类融合算法要经过多轮计算，才能达到较高精度，缺点是运算周期较长，并且需要人工判断并改进融合参数的设置，无法实现快速实时融合计算。

2.1　基于神经网络的快速数据融合

经过数据准备工作过程，得到参与融合的测量数据具有以下几个特点：

1) 数据对融合结果的贡献都是正向的。通过对数据异常信息的剔除结果可知，测量数据的误差可以理解为在其测量精度范围内随机分布；

2) 数据质量可以通过融合权重值客观反映。根据融合权重值设定过程可以看出，该值反映的是测量设备的精度范围，权重值越大，数据质量越高；

3) 数据的剩余误差可以通过多测元数据的融合计算加以消除。融合计算就是利用多测元的冗余信息，精确计算弹道真值，并能够对参与融合计算测量数据的系统误差进行估计。

根据以上几个特点，选择神经网络进行快速融合完全满足需求[10]。将各测元数据作为输入，融合权值作为神经网络权值，神经网络的输出就是快速融合弹道结果。

2.2　融合结果的统计分析

融合结果计算完毕还需要与各测元数据进行比对，一方面估算测元数据中存在的系统误差，另一方面还可以通过比对和统计分析发现融合结果中不合理的弹道数据，对测元数据进行修正。

首先，统计融合结果的方差，初步了解融合结果的相关信息。其次，将融合结果与各测元进行比对，分析比对结果与测量设备的系统误差特性是否相符。最后，分析比对结果中的异常数据，如果是测元数据异常，则将该异常数据剔除，再重新融合及比对；如果异常数据由融合结果引起，可以分析导弹飞行过程异常原因，为试验鉴定提供依据。

3实测数据验证

为验证快速融合算法的可靠性和精度，选择某次试验中参试4台2种类型设备数据进行快速融合计算，并以事后数据处理融合结果进行比对。4台设备测量数据分别标注为测元1~4，测量异常误差已在前期处理中剔除。考虑设备精度相近，融合权重均设为0.25。分离测元数据中的随机误差后，经第一次融合处理后各测元在X、Y、Z方向上与初步融合结果比对如图2~图4所示。

图2　X方向测元与初步融合结果作差

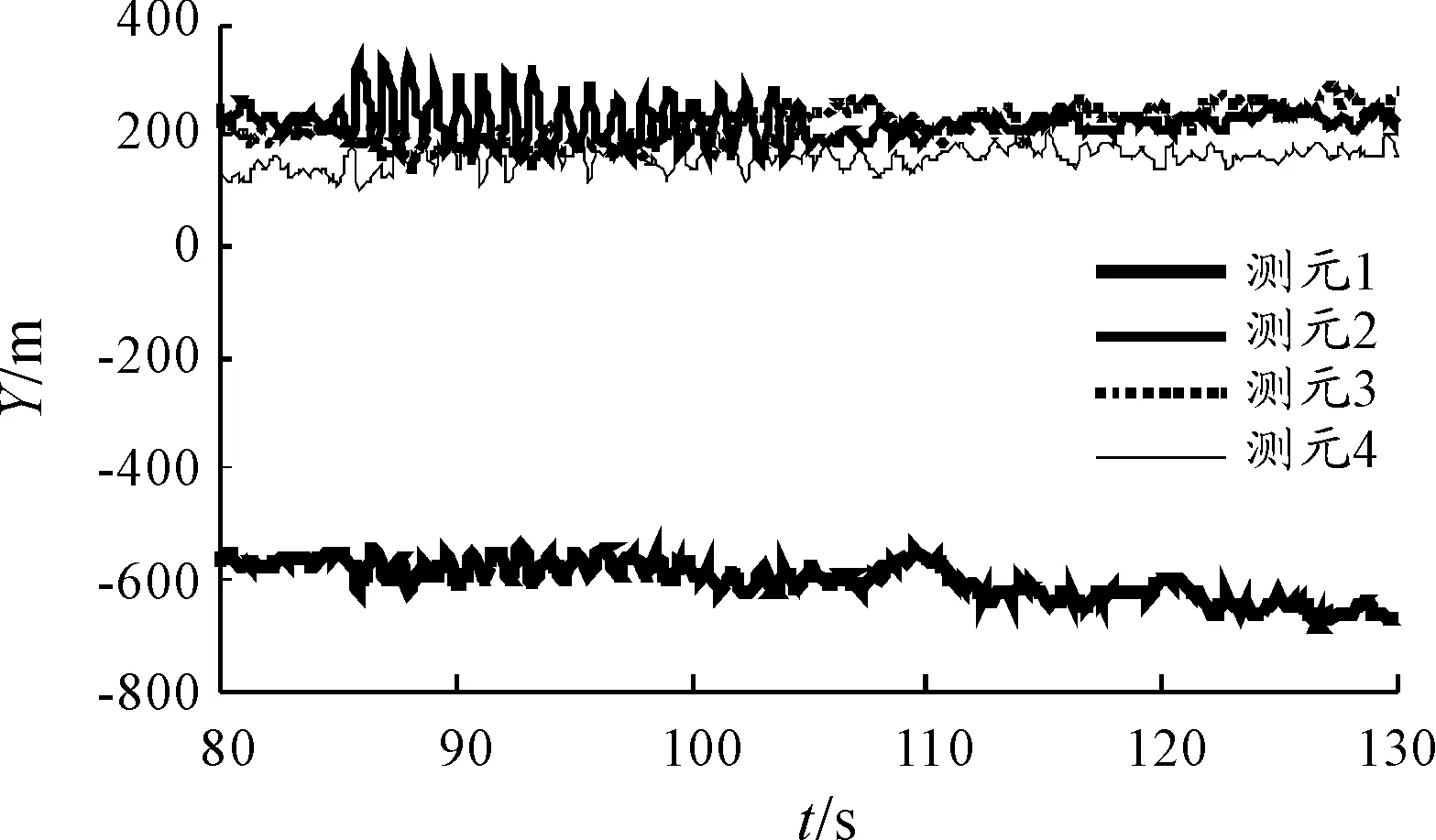
图3　Y方向测元与初步融合结果作差

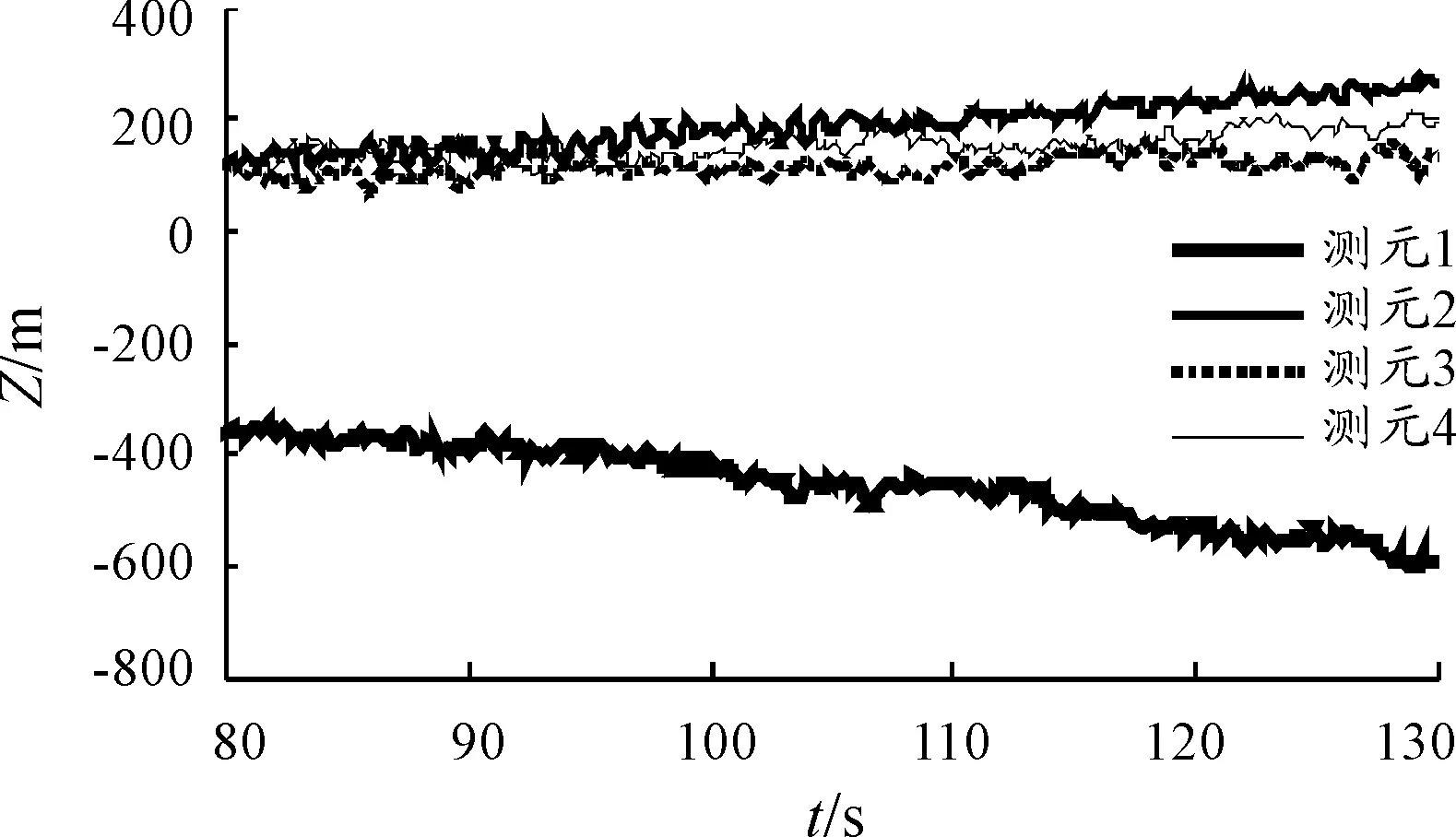
图4　Z方向测元与初步融合结果作差

从比对结果可以看出，测元1在与初步融合结果及其他3个测元数据差别都较大，需要对融合过程进行改进。剔除测元1后再对剩余3个测元进行重新融合，比对结果如图5~图7所示。

图5　X方向测元与改进融合结果作差

图6　Y方向测元与改进融合结果作差

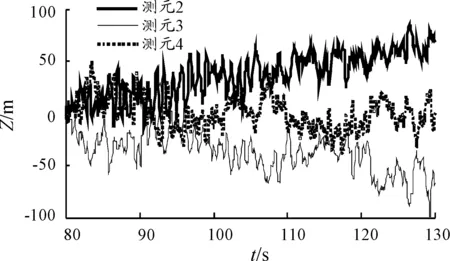
图7　Z方向测元与改进融合结果作差

图8给出了改进后融合结果与事后数据处理融合结果的比对分析，可以看出本文得到的融合结果与事后高精度融合结果相差很小，X、Y、Z方向残差的均方差分别为12.0m、18.1m、8.5m，完全满足常规试验对弹道结果的需求。

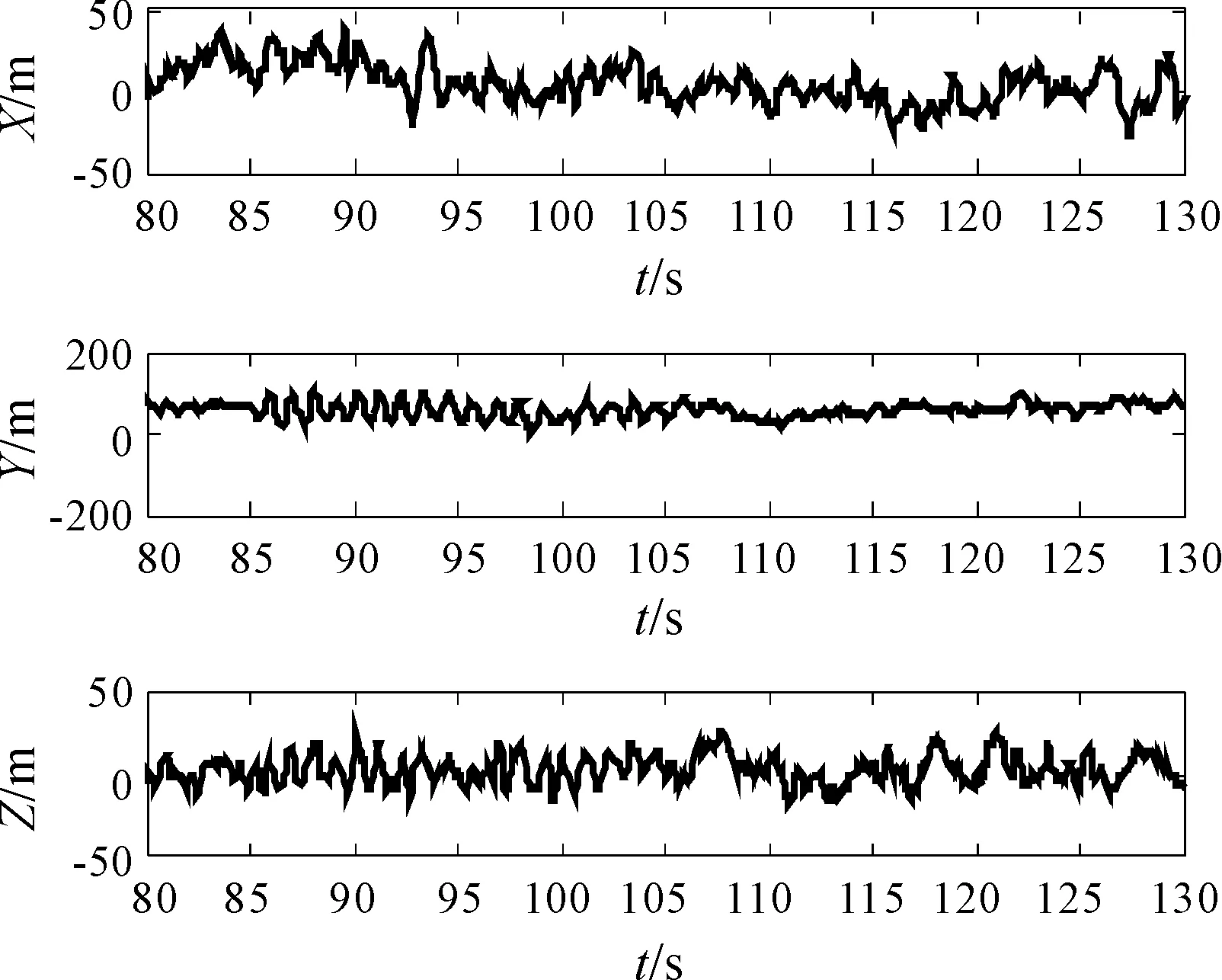
图8　改进融合结果与事后融合结果比对

通过对实测弹道数据的计算，本文的快速融合算法通过一次改进，就可以得到精度较高的融合弹道结果。通过进一步对排除的测元分析可以发现，该测元数据存在一个系统误差，为进一步分析该测量设备工作情况和故障排除提供依据。

4结论

利用测量数据实时、快速得到较高精度的融合弹道一方面可以实现异常弹道的快速诊断，另一方面可以对试验故障进行快速分析，还可以作为后期精细化弹道融合分析的基础。本文提出的快速融合方法避免理论弹道和初始弹道的限制，通过简单的处理可以得到精度较高的融合弹道结果。融合权值的设置还可以参考设备历史测量精度信息，充分利用武器试验信息化为数据处理带来的便利。同时，深入挖掘设备历史测量精度信息、客观评价设备工作状态也是本文进一步需要开展的工作之一。采用精度、稳定性更高的异常信息剔除算法以及结果比对统计分析方法也是拓展本文方法应用范围的可行途径。

参考文献：

[1]刘志栋.目标弹道数据实时融合方法研究[J].电子测量技术,2012,35(6):66-68.

[2]朱炬波.不完全弹道测量的数据融合技术[J].科学通报,2000,45(20):2236-2240.

[3]童丽,易东云.非线性融合模型的弹道估计精度评定[J].弹道学报,2002,14(4):1-5.

[4]胡圣波,徐云舟,毛太平.火箭飞行测量数据融合处理的一种算法[J].传感器技术,2005,24(8):68-70.

[5]姚尚,张承虎,秦德明，等.有翼飞行器外弹道测量数据融合处理研究[J].动力学与控制学报,2011:9(1):86-90.

[6]王正明.弹道跟踪数据的校准与评估[M].长沙:国防科技大学出版社,1999.

[7]李正东,何武良,郑晓东，等.一种改进的数据融合算法[J].光电工程,2001,28(5):65-68.

[8]王鹏,王雷,王中，等.数据融合技术在鱼雷空中弹道测试中的应用研究[J].舰船电子工程,2010,30(11):37-40.

[9]XiuyunDUAN,YuHUANG.ResearchonMethodofRandomErrorSeparationBasedonWaveletTransformandFrequencybandsCharacter[J].ComputerScienceandElectronicsEngineering.2013(7):2525-2528.

[10]倪国强,李勇量,牛丽红.基于神经网络的数据融合技术的新进展[J].北京理工大学学报,2003,23(4):503-508.

(责任编辑唐定国)

收稿日期：2015-02-11

作者简介：段秀云(1979—)，男，工程师，硕士，主要从事外测数据处理、遥外测联合数据处理研究。

doi:10.11809/scbgxb2015.07.042

中图分类号：TJ 013

文献标识码：A

文章编号：1006-0707(2015)07-0165-04

本文引用格式：段秀云,黄瑜.外弹道测量数据快速融合方法[J].四川兵工学报，2015(7):165-168.

Citationformat:DUANXiu-yun，HUANGYu.ResearchonMethodofFastFusionCalculationonTrajectoryData[J].JournalofSichuanOrdnance,2015(7):165-168.

ResearchonMethodofFastFusionCalculationonTrajectoryData

DUANXiu-yun，HUANGYu

(Unit94,theNo. 91550thTroopofPLA,Dalian116023,China)

Abstract:It is the important and basic work to calculate the trajectory result quickly and accurately. In the case of which the theoretical trajectory is invalided, or there is no high precision measurement equipment, a fast fusion trajectory calculation method based on the neural network was put forward. Firstly the fusion weight was set according to the measurement precision. Then the exceptional and random errors were eliminated. Finally the high precision trajectory result was computed and the system error of the measurement data was estimated. The actual data computing proves the reliability and precision of the method.

Key words:fast fusion calculation; fusion weight; exceptional error; neural network

_______________________

【基础理论与应用研究】