突防弹最优机动频率的选择问题研究

潘乐飞，刘新学，王顺宏

(第二炮兵工程大学，西安　710025)

突防弹最优机动频率的选择问题研究

潘乐飞，刘新学，王顺宏

(第二炮兵工程大学，西安710025)

摘要：为提高弹道导弹的生存概率，研究了突防弹的机动频率与拦截弹脱靶量之间的解析关系；基于比例导引的线性化模型，通过引入频域分析方法，分析了拦截弹脱靶量峰值与突防弹机动频率间的关系，获得了脱靶量峰值与目标弹机动频率之间的解析公式；通过仿真分析，验证了解析公式的合理性，具有一定的工程应用价值。

关键词：机动频率；脱靶量；比例导引；频域分析

弹道机动可以大大提高导弹的生存概率。合理的机动频率与机动幅值，会提前消耗拦截弹机动所需的有限燃料，若能在遭遇前使拦截弹燃料耗尽，则可达到机动突防的目的。目前研究最优突防与拦截的对抗问题时大都采用最优控制理论与博弈理论[1,2]。这两种方法均需要获取突防弹与拦截弹完备的飞行参数，但目前由于各种条件的限制我们无法获取攻防双方的完整信息，故上述理论暂不具备工程应用的条件。

对突防弹来说，尽管无法预知拦截弹的发射时间及遭遇时刻，但在某些条件下可事先获得拦截弹的导弹类型及相应的制导方案。因此，可以利用有限的拦截弹信息，研究突防弹机动频率及机动幅值对拦截弹脱靶量的影响。

本文假定已知拦截弹的制导方案及制导系统动力学参数(如拦截弹的有效导航比、制导系统时间常数、自然频率、阻尼系数等)，试图寻找拦截弹脱靶量与突防弹机动频率间的函数关系。

1比例导引线性化模型

拦截弹末制导系统的线性化模型[3]如图1所示。

图1　比例导引线性化模型

(1)

其中，对于有尾翼控制的导弹，有

(2)

对于非尾翼控制导弹a(s)是一阶多项式；ωM为自然频率；ζ为阻尼系数；ωz为弹体零频。

2脱靶量峰值计算

在复数域，tf时刻的脱靶量公式[4]为

(3)

式(3)中，YT(s)为目标弹垂向位置YT(t)的拉普拉斯变换；Y(tf,s) 为y(tf)的拉普拉斯变换；H(s)=G(s)/s，其中

(4)

式(4)中，r1、r2、r3为常值系数。

若目标机动方式为正弦形式(nT=1gsinωT)，则由于目标机动频率ω产生的脱靶量稳态分量为

(5)

其中，P(tf,iω)为tf时刻由于目标机动频率ω产生的脱靶量。

(6)

其中，系数A、B1、B2、C和D可以计算如下

A=1

对于τ2=0，有

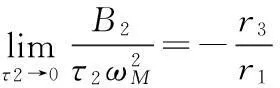
对第4项进行积分，得

(7)

由于仅考虑目标机动频率对脱靶量的影响，故将s=iω代入式(7)，得

(8)

在式(7)、式(8)中，arctan表示对复变量的反正切，tan-1表示在含有复数的对数函数中的实数部分进行的反正切。

仅考虑上式的实数部分，代入积分公式，解得

(9)

其中，

(10)

根据上面得到的脱靶量幅值特性函数式(9)、式(10)可知，当目标机动频率ω变化时，脱靶量幅值必然存在极值。

3仿真分析

令导航系数N=4，ωM=20 rad/s，ωz=5 rad/s，τ=0.5 s，ζ=0.7。根据式(9)、式(10)可得仿真结果如图2所示。脱靶量峰值大概发生在ω=1.7 rad/s处，且随着目标机动频率的增加，脱靶量峰值又逐渐减小。分析可知，当机动频率ω逼近零时，其效果类似于阶跃机动，故脱靶量峰值也逼近为零；而当机动频率ω过大时，会使其有效机动幅值减小，故脱靶量峰值反而又趋向于零。

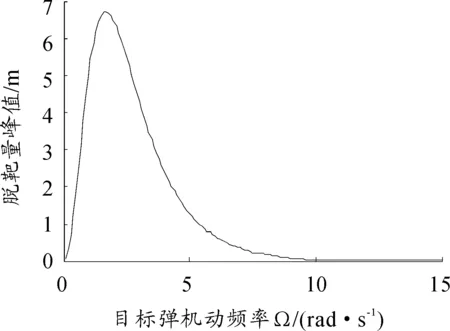
图2　脱靶量峰值与目标弹机动频率的关系曲线

令ω=1.4 rad/s，目标机动加速度为nT=1gsinω，根据图1线性化模型进行仿真，可得拦截弹的脱靶量与剩余飞行时间的关系曲线(图3)。由于目标弹作正弦机动的缘故，拦截弹脱靶量峰值随飞行时间也呈正弦变化规律，其最大值在6.7左右，与图2 的仿真结果接近，即验证了式(9)、式(10)的计算结果。

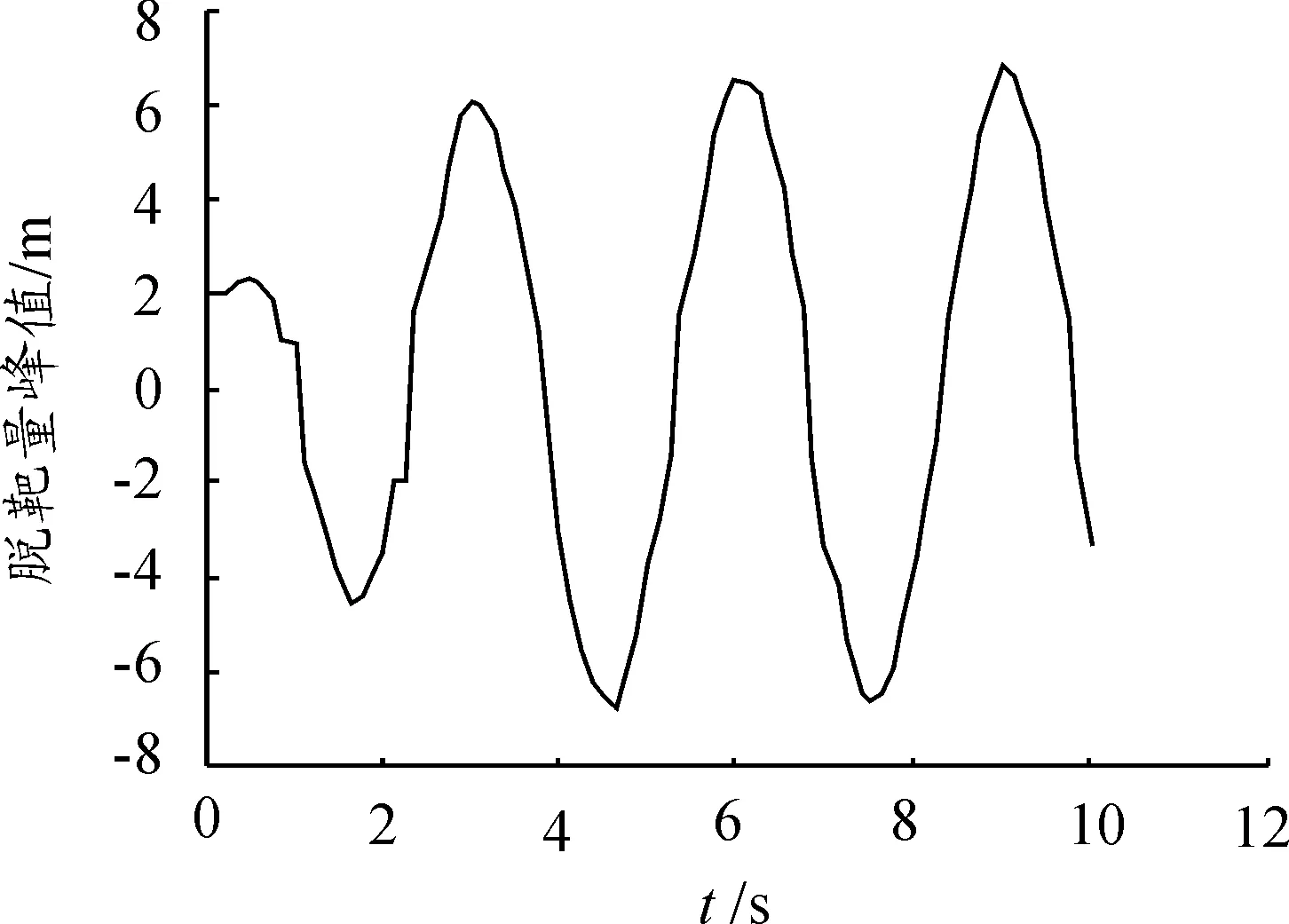
图3　脱靶量峰值与待飞时间关系曲线

由于对脱靶量峰值起决定作用的因素为目标机动频率ω及拦截弹时间常数τ，且有拟合公式[3]：

因此，固定N=4，ωM=20rad/s，ωz=5rad/s，ζ=0.7时，令拦截弹时间常数τ由0.2逐渐增加至1.0，可得脱靶量峰值及对应最优机动频率的数据(表1)。由仿真数据可知，随着时间常数τ的递增，脱靶量峰值逐渐减小，最优机动频率ω逐渐减小。

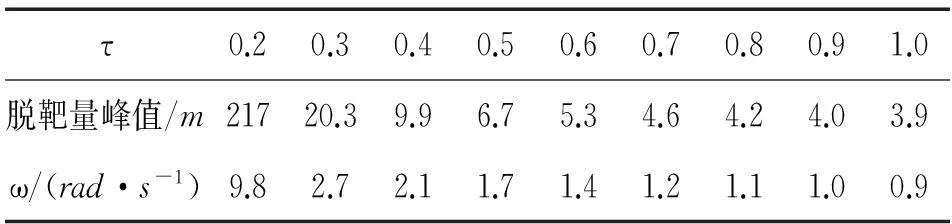
表1　时间常数τ与脱靶量峰值及机动频率ω的关系

4结论

本文研究了目标作正弦机动的频率与拦截弹脱靶量峰值的关系。理论公式和仿真结果表明：选择合理的目标机动频率能够使拦截弹产生稳态脱靶量。在实际的攻防对抗中，由于无法精确获得拦截弹的制导系统参数，因此需要进一步探讨如何在实战中合理使用本文的理论公式。

参考文献：

[1]马骏声.博弈论—机动弹头攻防的核心[J].航天电子对抗,2006,2(1):4 -7.

[2]雷刚，田海鹏，鲜勇，等.基于博弈论的导弹机动突防策略研究[J].固体火箭技术，2014,37(3):291-294.

[3]ZarchanPaul.Proportionalnavigationandweavingtargets[J].JournalofGuidanceControlandDynamics,1995,18(5):969- 974.

[4]RafaelYanushevsky.Analysisofoptimalweavingfrequencyofmaneuveringtargets.JournalofSpacecraftandRockets,2004,41(3):477-479.

[5]姜玉宪，崔静.导弹摆动式突防策略的有效性[J].北京航空航天大学学报，2002，28(2)： 133-136.

[6]顾文锦，赵红超，王凤莲.反舰导弹末端机动的突防效果研究[J].宇航学报，2005，26(6)：758-763.

[7]钱广华， 李颖，骆荣剑. 一种新的机动频率和方差自适应滤波算法[J].重庆理工大学：自然科学版，2013(5):86-89.

(责任编辑杨继森)

收稿日期：2015-02-14

作者简介：潘乐飞(1979—)，男，博士研究生，讲师，主要从事飞行动力学与制导研究。

doi:10.11809/scbgxb2015.07.023

中图分类号：V448

文献标识码：A

文章编号：1006-0707(2015)07-0090-03

本文引用格式：潘乐飞，刘新学，王顺宏.突防弹最优机动频率的选择问题研究[J].四川兵工学报，2015(7):90-92.

Citation format:PAN Le-fei, LIU Xin-xue, WANG Shun-hong.Optimal Frequency of Weaving Maneuver Penetration[J].Journal of Sichuan Ordnance,2015(7):90-92.

Optimal Frequency of Weaving Maneuver Penetration

PAN Le-fei, LIU Xin-xue, WANG Shun-hong

(The Second Artillery Engineering University, Xi’an 710025, China)

Abstract:To improve the penetration probability of ballistic missiles, the analytic relationship between the weaving penetration frequency and the interceptor miss distance was studied. Based on the linear model of proportional navigation, introducing the Laplace transition method in the complex domain, the relationship and analytic formula between the max miss distance and weaving frequency were obtained. The simulation results show the rationality and certain engineering application value of the analytical formula.

Key words:weaving frequency; miss distance; proportional navigation; complex domain analysis

_______________________

【信息科学与控制工程】