查漏补缺之数列

重难点讲解

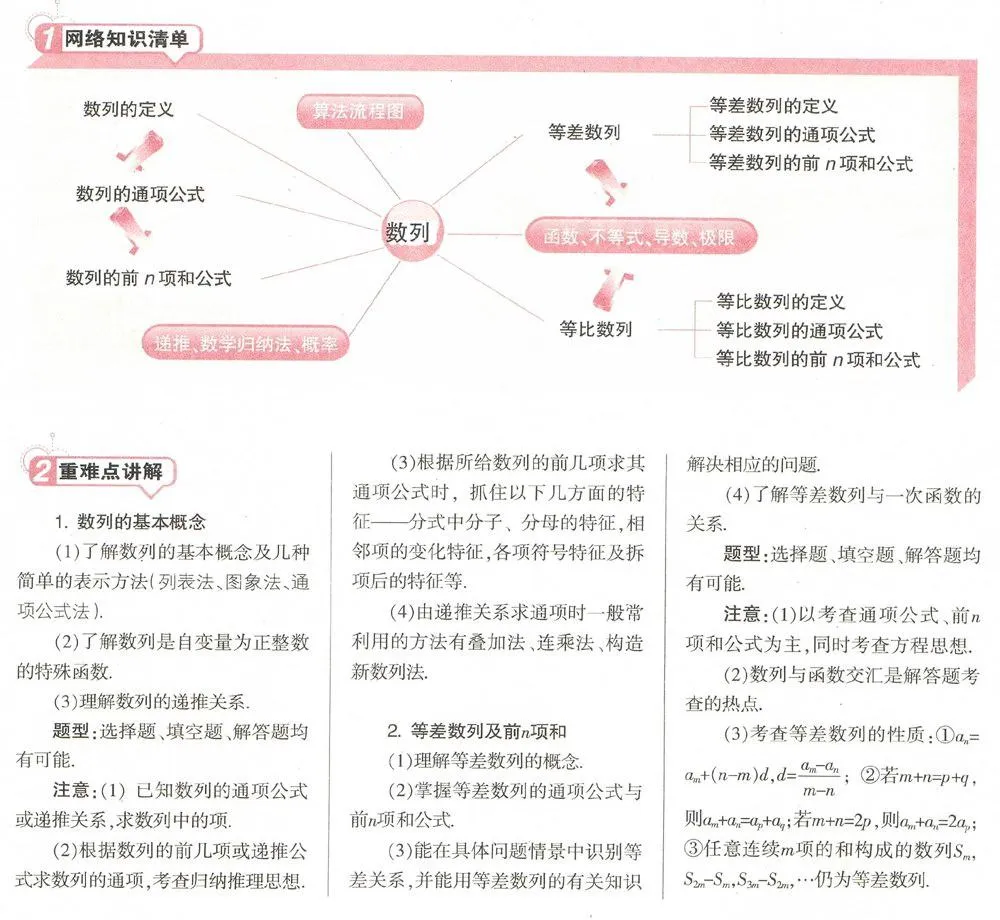
1.数列的基本概念

（1）了解数列的基本概念及几种简单的表示方法（列表法、图象法、通项公式法）.

（2）了解数列是自变量为正整数的特殊函数.

（3）理解数列的递推关系.

题型：选择题、填空题、解答题均有可能，

注意：（1）已知数列的通项公式或递推关系，求数列中的项.

（2）根据数列的前几项或递推公式求数列的通项，考查归纳推理思想.

（3）根据所给数列的前几项求其通项公式时，抓住以下几方面的特征——分式中分子、分母的特征，相邻项的变化特征，各项符号特征及拆项后的特征等.

（4）由递推关系求通项时一般常利用的方法有叠加法、连乘法、构造新数列法.

2.等差数列及前n项和

（1）理解等差数列的概念.

（2）掌握等差数列的通项公式与前n项和公式.

（3）能在具体问题情景中识别等差关系，并能用等差数列的有关知识解决相应的问题

（4）了解等差数列与一次函数的关系.

题型：选择题、填空题、解答题均有可能.

注意：（1）以考查通项公式、前n项和公式为主，同时考查方程思想.

（2）数列与函数交汇是解答题考查的热点.

（3）考查等差数列的性质：① ；②若m+n=p+q，则a_m+a_n=a_p+a_q；若m+n=2p，则a_m+a_n=2a_p；③任意连续m项的和构成的数列S_m，S_2m-S_m，S_3m-S_2m，…仍为等差数列，

3.等比数列及前n项和

（1）理解等比数列的概念.

（2）掌握等比数列的通项公式与前n项和公式.

（3）能在具体问题情景中识别等比关系，并能用等比数列的有关知识解决相应的问题.

（4）了解等比数列与指数函数的关系.

题型：选择题、填空题、解答题均有可能，

注意：（l）以考查通项公式、前n项和公式为主，同时考查等差数列及等比数列的综合应用.

（2）数列与函数交汇是解答题考查的热点.

（3）考查等比数列的性质：

①

②若m+n=p+q，则a_m·a_n=a_p·a_q；若

③任意连续m项的和且不为零时构成的数列S_m，S_2m-S_m，S_3m-S_2m，…仍为等比数列.

4.数列求和

（1）熟练掌握等差、等比数列的前n项和公式.

（2）掌握非等差、等比数列求和的几种常见方法：倒序相加法、错位相减法、裂项相消法、分组求和法.

题型：选择题、填空题、解答题均有可能，

注意：（l）以考查等差、等比数列的求和公式为主，同时考查转化与化归思想.

（2）对非等差、等比数列求和，主要考查观察能力，分析问题和解决问题的能力及计算能力.

（3）数列求和常与函数、方程、不等式等诸多知识联系在一起，具有复杂多变、综合性强、解法灵活等特征，易成为高考的中档题或压轴题.

5.数列的综合应用

（1）能在具体问题情景中识别数列的等差、等比关系，选用相应知识解决问题，熟记以下几个常见的结论：若{a_n}，{b_n}为等差数列，则{ka_n+tb_n}为等差数列；若{a_n}，{b_n}为等比数列，则 为等比数列；若{a_n}为等差数列，则{C_an} （c>0）为等比数列；若{b_n}（b_n>0）为等比数列，则{loa_cb_n}（c>0且c≠1）为等差数列.

（2）在实际问题中会用等差、等比数列建立模型解决问题.

题型：主要以解答题为主.

注意：（1）等差、等比数列交汇.

（2）考查数列的基本计算.

（3）数列与函数、概率、不等式、解析几何的综合应用以考查数列知识为主，同时考查化归、转化等数学建模能力.

（4）等比数列的前n项和公式的常见应用题

1.数列的性质

数列的单调性：若恒有a_nn+1，则数列严格递增；若恒有a_n>a_n+1，则数列严格递减.等差数列若公差d>0，则数列单调递增；若公差d<0，则数列单调递减.等比数列若a₁>0，公比q>l，则数列单调递增；若a₁<0，公比O1<0.公比q>l，则数列单调递减；若a₁>0，公比O

2.由递推数列求通项

（1）直接利用等差、等比的通项公式求解.

（2）利用a_n和S_n的关系求解：a_n=

（3）归纳一猜想一证明法.

（4）非等差、等比数列转化为等差或等比数列：

①形如a_n+1=Aa_n+B（A≠1且AB≠0）.设a_n+1+x=A（a_n+1+x）（其中x是待定的系数），所以（A_l）x=B， ，故 是等比数列.

②形如a_n+1=Aa_n+B·Cⁿ⁺¹（A≠C，C>O，C≠1）.常变形为 ，设 ，故 ，根据①可得 是等比数列，进而求得a_n

③

④ 求解方式同①.

（5）形如a_n+1=a_n+f（n）的递推数列求通项，用累加法；形如a_n+1=f（n）·a_n的递推数列求通项，用累乘法.

（6）已知 ，可以结合S 的关系式，也可以写成关于 的关系式，选取的标准是哪个关系式比较容易求解就选哪个.

3.数列不等式证明

（l）证明数列a_n>m（或

（2）证明连续和，每一项放缩成可以裂项相消的形式.

（3）证明连续积，每一项放缩成可以错位相乘的形式.

（3）用数学归纳法证明.

（4）对于证明存在问题、唯一问题、大小问题等有时可以尝试反证法.