框架-剪力墙结构中剪力墙刚度的优化
曾德淼
(上海民航新时代机场设计研究院有限公司广州分公司 广东广州 510000)
框架-剪力墙结构中剪力墙刚度的优化
曾德淼
(上海民航新时代机场设计研究院有限公司广州分公司广东广州510000)
框架-剪力墙结构是建筑工程的主要结构形式之一,在此结构中,剪力墙的刚度是影响建筑工程安全和经济性的重要因素,对剪力墙结构刚度进行优化十分必要。本文就在考虑框剪结构剪力墙刚度影响因素的基础上,提出剪力墙刚度优化的设计方案,并以广州新白云机场为案例进行计算验证,为框剪结构剪力墙刚度优化提供一定参考。
框架-剪力墙结构;剪力墙刚度;优化设计
框架-剪力墙结构综合了框架结构和剪力墙结构的优点,不仅能够为建筑提供大空间,也可以保持建筑良好的抗震性能,在我国高层建筑中有着广泛结构。在框剪结构中,剪力墙承担着绝大部分的水平荷载,所以,剪力墙的刚度大小决定着框剪结构建筑的安全性。在剪力墙设计中,剪力墙数量越多,其水平抗震能力越强,但经济性越差,所以,需要从抗震性与经济性矛盾中寻找平衡点,也就是最佳剪力墙刚度[1]。
1 框架-剪力墙结构中剪力墙刚度的优化设计
1.1确定数学模型目标函数
在框架-剪力墙结构中,如果剪力墙的刚度设计越小,其地震作用也会相应减小,增大房屋的变形,无法起到抵抗水平地震的功能;如果剪力墙刚度设计较大,可以有效减小房屋的自振周期,增强对水平地震的抵抗能力,保证房屋安全;但是,越大的剪力墙刚度需要越多的剪力墙数量,会增加建设成本,所以,必须对剪力墙刚度进行优化设计,在保证剪力墙刚度满足建筑需求基础上,提高剪力墙的经济性。
为实现上述目标,将剪力墙刚度优化简化为求剪力墙等效截面惯性矩的数学模型,目标函数是使水平地震荷载趋向于最小值。
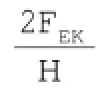


图1 剪力墙地震作用简图
将(2)式代入(1)式,可得:

为简便计算,地震作用计算采用底部剪力法,其标准值为FEK,计算公式为:

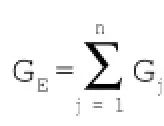
从公式(3)中可知,结构基本自振周期(T1)与剪力墙刚度(EcIeq)是反比关系,同时,根据α1取值,T1与地震荷载也是反比关系,所以,剪力墙刚度与地震荷载是正比关系,即剪力墙刚度越大,地震荷载也越大。
在考虑高层建筑弯曲振型的影响因素下,取出部分地震力ΔFn=δnFEK,δn是顶部附加水平地震作用系数,将其移到顶层,剩余地震力分配到其它楼层中,可得:

式中:Hi和Hj表示第i层、j层的层高。
在本文中,为简化计算,在通过公式(4)计算得到底部剪力标准值后,未将ΔFn取出,而是根据图1所示倒三角,将其分配到各楼层中,每层楼受力为:

之后,对连续分布倒三角分布荷载进行简化,根据基底弯矩相等原则可得:

在高层建筑物中,由于整体高度较高,公式(7)中第二项值很小,可以忽略不计,则有:

将公式(3)、(4)代入(8)中,可得:
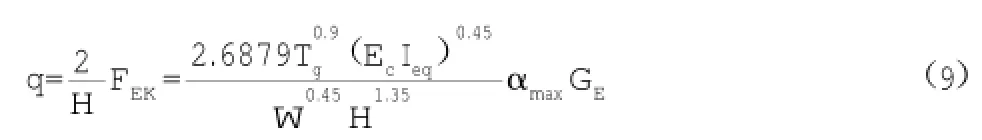
也就是剪力墙结构优化设计的目标函数。
1.2确定设计变量
依据图1所示,在倒三角水平荷载作用下,剪力墙在一个主轴方向上任一点都会发生水平位移:
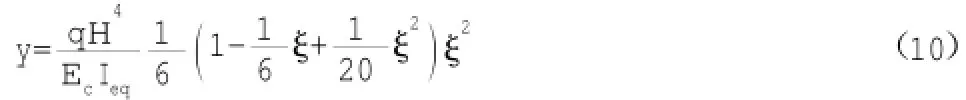
式中:y代表剪力墙某点上的水平位移;EcIeq为总剪力墙的等效刚度,以此为基础,可得结构层间位移计算公式为:


结构顶点位移为:

以既有建筑方案为例,设剪力墙截面参数的厚度和长度分别为tu和hu,则第i道剪力墙的厚度和长度可以用tui、hui表示,对应的设计变量为剪力墙等效刚度EcIui。在实际建设当中,剪力墙的抗剪强度还会受到开洞面积的影响,可以分为整体墙、联肢墙、整体小开口墙几种类型。对于剪力墙结构而言,在一个主轴方向上,在水平荷载作用下,不同类型墙体都会发生的顶点位移,将所有定点位移抗侧等效刚度迭加,就能够得到总抗侧刚度EcIeq,因此,为简便计算,设计变量选择为EcIeq[3]。
1.3限定约束条件
根据相关规范的要求,在框剪结构剪力墙刚度设计当中,需要保证其满足刚重比、几何尺寸、轴压比、层间位移角和受剪承载力等基本要求,约束条件有以下几项:
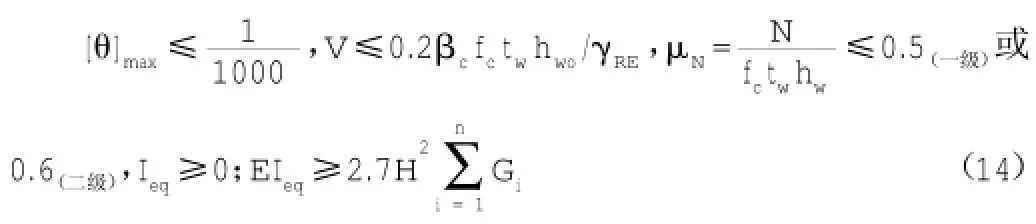
1.4求解并进行程序设计
在上述框剪结构剪力墙刚度设计中,公式(9)、(14)所代表的优化模型属于非线性规划问题,设计变量与目标函数之间是单调递增函数,设计变量只有一个,在求解过程中,可以按照一维搜索法的0.618法来计算得到最优解,然后根据约束条件和工程经验来确定搜索区间,并运用MATLAB软件来编制相应的优化程序,为剪力墙结构水平地震作用下抗侧刚度的优化计算提供依据[4]。
2 广州新白云国际机场实例计算
2.1工程实例概况
以广州白云国际机场为例,航站主楼采用的是框架-剪力墙钢筋混凝土结构,钢筋混凝土楼盖柱网为18m×18m,建筑面积共140000m2,结构最大程度为325m,地下部分不分缝,地上部分有三道,将主楼混凝土平面划分成6个结构单元,在6个结构单元中,最大程度为96m,剖面图见图2。

图2 主楼剖面图
主楼东西两侧均有连接楼,连接楼长宽分别为450m和62m,地上结构为3层,楼盖部分柱网也是18m×18m,东西两翼连接楼建筑总面积约为120000m2。在每个连接楼上,有三道伸缩缝,将连接楼混凝土平面平均划分成4个结构单元,每个结构单元长度约为108m,连接楼剖面图见图3。

图3 连接楼剖面图
此外,东西两侧还分别有两条指廊,总面积约90000m2,分别用东一、东二和西一、西二表示,其中,东一、西一指廊的长宽为360m、38.m;东二、西二指廊的长宽为252m、38.8m。在东一、西一指廊中有三道伸缩缝,划分成4个结构单元;在东二、西二指廊中有二道伸缩缝,划分成3个结构单元;每个结构单元长度为84m,指廊剖面图见图4。

图4 指廊剖面图
在此工程中,取不同尺寸的剪力墙,分别用XSW-2、XSW-3、XSW-4、XSW-5、XSW-6表示,并用MATLAB软件编制计算程序,剪力墙刚度情况与优化计算结果如表1~3所示。
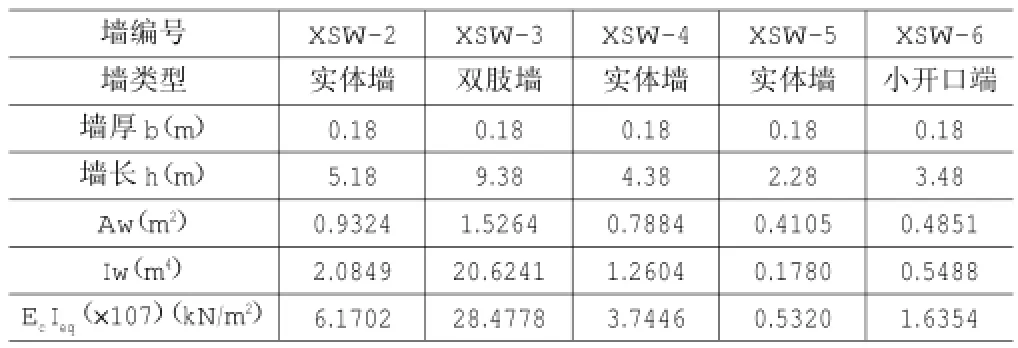
表1 不同类型剪力墙的初始等效刚度
3 结语
框架-剪力墙结构的剪力墙刚度与建筑安全有着密切联系,本文就根据剪力墙刚度与水平地震作用的关系,建立相应的剪力墙刚度优化模型,并使用MATLAB软件进行优化计算,为框架-剪力墙结构中的剪力墙刚度优化设计提供参考。
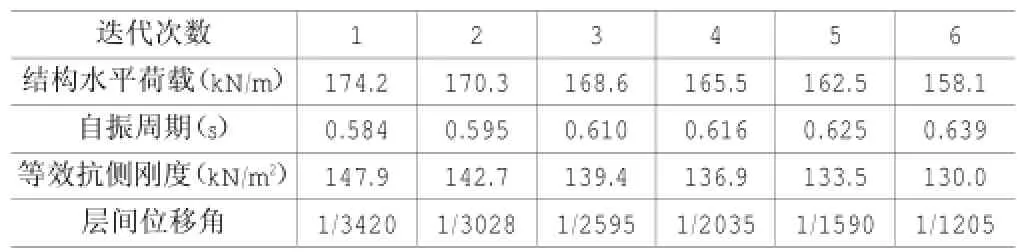
表2 剪力墙刚度优化结果
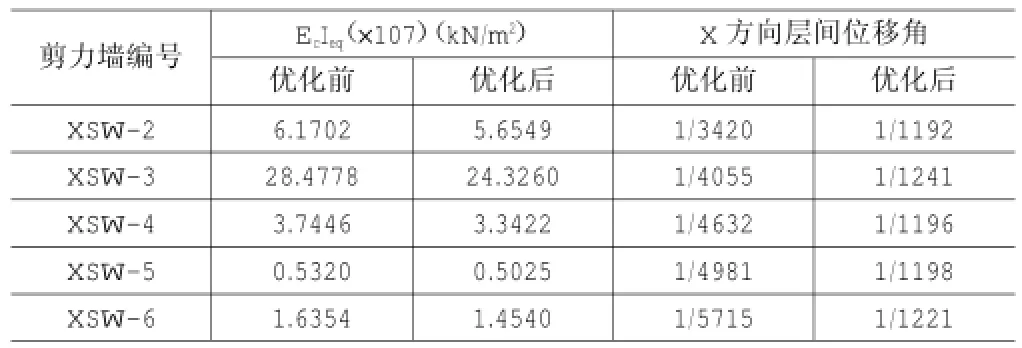
表3 平行于X轴的剪力墙优化前后刚度
[1]陈鹏,黄晓春,尹锐.框架-剪力墙结构中剪力墙数量的优化分析[J].泰州职业技术学院学报,2010,01:61~63.
[2]申志磊.框架剪力墙结构中剪力墙布置的优化设计[J].科技与创新,2015,17:112.
[3]杨阳,黄慎江,李自祥.变刚度框剪结构的剪力墙刚度优化[J].工程与建设,2012,02:197~199+239.
[4]贺海斌,朱学文.高层剪力墙结构中剪力墙抗侧刚度的优化设计研究[J].工程建设与设计,2011,09:58~61.
TU398.2
A
1673-0038(2015)44-0005-03
2015-10-11
曾德淼(1985-),男,工程师,硕士,主要从事结构设计工作。

