基于公理化设计矩阵与设计结构矩阵的滴灌灌水器创新设计
陈兴强,赵 泽,苏小虎,刘春景
(蚌埠学院 机电系,安徽 蚌埠 233030)
引言
滴灌灌水器的水力性能直接影响滴灌质量.灌水器的水力性能取决于灌水器流道的结构参数,因此滴灌滴头流道结构创新设计最为重要[1-3].
创新性设计理论对滴灌产品的设计至关重要,目前国内外大量学者致力于该领域的研究.Suh等[4-7]提出公理化设计准则(Axiomatic Design),公理化设计准则可为滴灌产品的创新设计提供相关思维方法.Steward[8]基于设计结构矩阵DSM(Design Structure Matrix)提出了复杂系统的设计方法.Robotham[9]、Malmqvist等[10]和曹兴东等[11]基于功能方法树提出了产品方案设计和方案评估的关键技术.发明问题解决理论(TRIZ)[12]揭示了产品创新设计的内在规律和原理,为滴灌产品的创新设计提供了基本思路.
本文以滴灌灌水器水力性能为目标函数,基于公理化设计、分析性稳健设计原理和设计结构矩阵建立滴灌灌水器流道结构分析性设计模型.
1 公理化设计原理及设计结构矩阵
传统设计是基于经验的设计,费时费力.基于公理化设计原理,设计者首先把用户的需求转换为产品的功能需求,根据产品功能需求确定产品零部件的结构及相关参数,最后对产品零部件进行工艺设计从而确定相关工艺参数[13].公理化设计原理主要由用户域、功能域、物理域、过程域等组成,从功能域到物理域,从物理域到过程域,公理化设计应用按层级在相邻两域之间以“之”字形映射方式进行问题求解[13].
设计结构矩阵是由Steward提出用于分析和规划产品设计的数学工具,Eppinger在设计结构矩阵的基础上又提出了数字化的设计结构矩阵[14].基于DSM可以洞悉产品零部件的结构及相关参数设计中的潜在问题,为产品设计中的工程变更及优化提供有效支持[13].
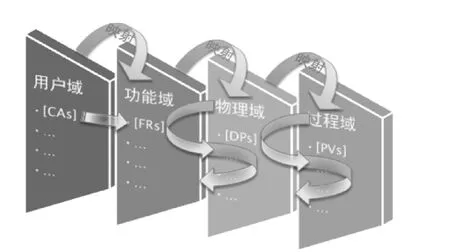
图1 公理化设计中“之”字形映射
2 基于公理化设计矩阵与设计结构矩阵的灌水器流道设计同步演化

式中:ST——滴灌灌水器流道功能需求原理;Θ——功能需求原理的领域;λsatisfy——基于ST原理功能需求求解;DM——滴灌灌水器流道公理化设计矩阵;DP——滴灌灌水器流道参数.
将功能实施原理通过一定的结构形式在工程技术上加以应用,就是所谓的技术效应[13].技术效应可以用设计结构矩阵DSM来描述,即

由式(3)、(4)可知,可由公理化设计矩阵DM中的主要设计参数得到设计结构矩阵DSM,即

由于滴灌灌水器流道结构复杂,且流道结构尺寸大多处在微尺度领域,滴灌灌水器流道设计的设计结构矩阵不便直接获取.因此基于公理化设计原理,从滴灌灌水器功能域到物理域的映射关系推导建立设计结构矩阵变得极为重要.公理化设计设计矩阵只能映射不同域之间的关系,不能解释域内结构因素之间的关系.设计结构矩阵只能静态的解释产品的功能与各结构因素之间的关系.
因此提出复合矩阵CM(Composite Matrix)的思想,搭接公理化设计矩阵与设计结构矩阵之间的桥梁——(DM→CM→DSM),综合公理化设计矩阵与设计结构矩阵的优点,实现滴灌灌水器流道设计的公理化设计矩阵与设计结构矩阵同步演化过程.
滴灌灌水器流道设计公理化设计矩阵和设计结构矩阵同步演化的过程如下:
基于公理化设计原理构建滴灌灌水器流道设计的功能域到物理域之间的设计矩阵DM,识别DM中的主要灌水器流道设计参数,得到复合矩阵CM(见图2).
有淋巴转移的宫颈鳞癌中PTTG、VEGF-C、VEGFR-3表达阳性率及LMVD高于无淋巴转移的宫颈鳞癌(P<0.05)。见表2。
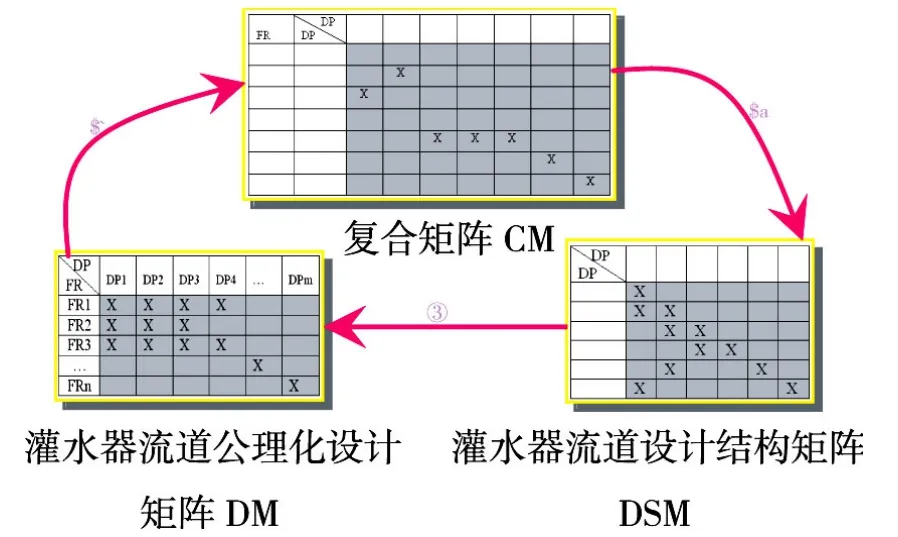
图2 滴灌灌水器流道公理化设计和设计结构矩阵同步演化
根据复合矩阵CM,结合各种设计约束(流态指数、流量系数、流量),构建滴灌灌水器流道设计结构矩阵DSM.
结合公理化设计的相关公理和推论判断滴灌灌水器流道设计结构矩阵是否合理,不合理则继续同步演化过程的第一步.
3 滴灌灌水器流道水力功能需求关系模型
基于公理化设计原理,产品的设计过程就是基于“之”字形映射方式从功能域到物理域进行问题求解的过程[15-16].在滴灌灌水器流道参数设计中,若fi(·)代表灌水器流道设计参数到第i个滴灌灌水器功能需求目标之间的映射关系,则

式中:Fi——功能目标,i=1,2,…,n;DPj——设计参数,j=1,2,…,m.
灌水器流道设计结构参数DPj(j=1,2,…,m)的标准值用μj=(j=1,2,…,m)表示,灌水器灌溉功能函数值用Fi表示,灌溉功能函数值变动量用△Fi表示,即

假设灌水器流道灌溉功能函数fi(·)在设计范围内关于设计参数连续并且高阶可导,由Taylor展开式的性质可知[15]
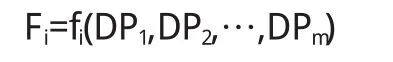
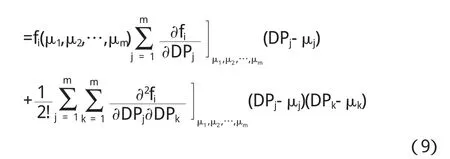
因此灌水器流道功能函数值的变动量可用(10)式表示.
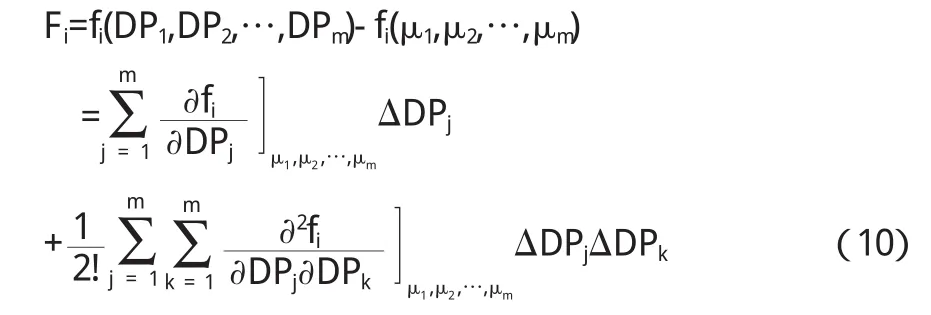
由(10)式可知
根据(10)式可知,展开式由不可控因素的一次项、平方项以及交叉项所组成[15],因此
△F=(△F1,△F2,…,△Dn)T,△F——系统功能特性变动量.
△DP(△DP1,△DP2,…,△DPm)T,△DP——设计参数变动的一次项.
△DPS=(△DP12,△DP22,…,△DPm2)T,△DPS——设计参数变动的平方项,△DP1——设计参数变动的交叉项.
因此,滴灌灌水器系统灌溉功能特性变动量模型如(11)式所示.

式中:D、F、G——系统设计结构矩阵.
4 滴灌灌水器创新设计
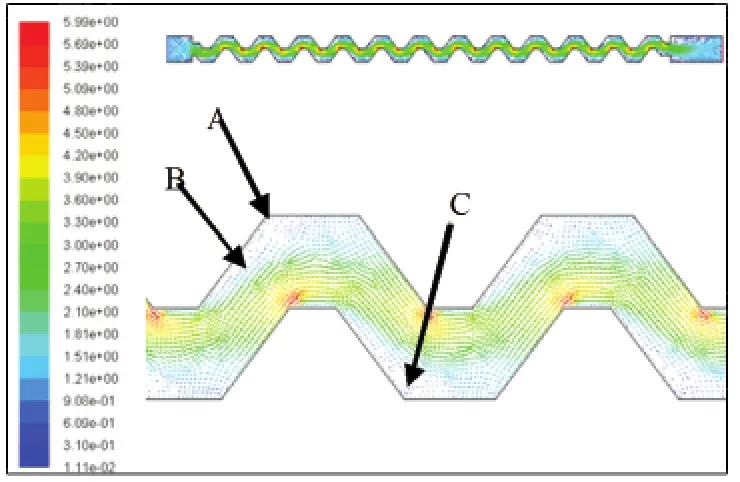
图3 速度矢量分布图

图4 速度矢量放大分布图
如图3、4所示,传统设计的滴灌灌水器流道中常会出现滞止区(A)、涡旋区(B)、低速区(C),滞止区、涡旋区、低速区的存在会严重影响滴灌灌水器的水力性能,尤其是引起灌水器流道的堵塞[16].本文以灌水器流道内部的流场分布为基础,以去除流道的滞止区、涡旋区、低速区为优化目标,基于公理化设计与设计结构矩阵进行滴灌灌水器设计.梯形迷宫流道结构如图5所示.
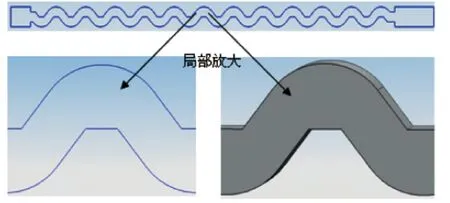
图5 创新设计后流道结构图
基于公理化设计矩阵与设计结构矩阵设计的滴灌灌水器梯形迷宫流道流场图如图6、7所示.
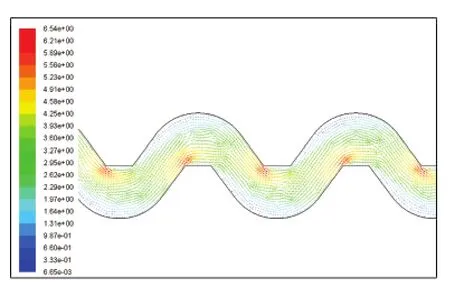
图6 创新设计后流道单元段速度矢量分布图
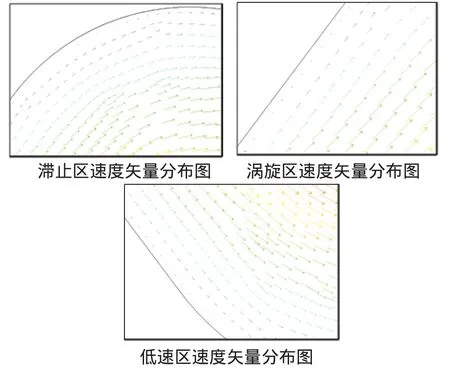
图7 创新设计后速度矢量放大分布图
5 结论
(1)本文基于公理化设计矩阵与设计结构矩阵提出了滴灌灌水器流道结构优化设计方法.
(2)构建了基于公理化设计矩阵与设计结构矩阵的滴灌灌水器流道设计分析性模型.
(3)基于公理化设计矩阵与设计结构矩阵设计的滴灌灌水器流道,水力性能得到了完全改善,流道内的滞止区、涡旋区、低速区已基本消除.
〔1〕张彦群,王建东,龚时宏,等.滴灌条件下冬小麦田间土壤蒸发的测定和模拟[J].农业工程学报,2014,30(7):91-98.
〔2〕杨小振,张显,马建祥,等.滴灌施肥对大棚西瓜生长、产量及品质的影响[J].农业工程学报,2014,30(7):109-118.
〔3〕史文娟,马媛,徐飞,等.不同微尺度膜下滴灌棉田土壤水盐空间变异特性[J].水科学进展,2014,25(4):585-593.
〔4〕Suh N. P. The Principles of Design [M]. Oxford University Press Inc, USA, 1990.
〔5〕Suh N. P. Axiomatic Design: Advances and Applications[M]. Oxford University Press Inc, USA, 2001.
〔6〕Suh N. P. A Theory of Complexity, Periodicity, and Design Axioms [J]. Research in Engineering, 1999, 11,116-131.
〔7〕Suh N. P., Sekimoto S. Design of Thinking Design Machine[J]. Annals of the CIRP, 1990, 39, 145-148.
〔8〕Steward D. V. The Design Structure System: A Method for Managing the Design of Complex Systems [J]. IEEE Transactions on Engineering Management, 1981, EM-28(3), 71-74.
〔9〕Robotham A. J. The Use of Function-Means Tree for Modelling Technical, Semantic and Business Functions[J].Journal of Engineering Design, 2002, 13(3), 243-251.
〔10〕Malmqvist J., Schachinger P. Towards an implementation of the chromosome model –focusing the design specification[C]. International Conference on Engineering Design ICED97, Tampere, August 19-21,1997.
〔11〕曹兴东,檀润华,苑彩云.基于功能分解的产品概念设计[J].机械工程学报,2001,37(11):13-17.
〔12〕Terninko J., Zusman A. Systematic Innovation: An Introduction to TRIZ [M]. CRC Press LLC, New York, 1998.
〔13〕唐敦兵,钱晓明,刘建刚.基于设计结构矩阵DSM 的产品设计与开发[M].北京:科学出版社,2009.
〔14〕孙亚东,张旭,宁汝新等.基于层次化设计结构矩阵的复杂产品研发过程研究[J]. 机械工程学报,2011,47(16):166-175.
〔15〕张健,顾佩华,包能胜等.非线性机械系统分析性稳健设计[J].机械工程学报,2009,45(10):207-215.
〔16〕刘春景.基于CAD/CFD 的滴灌滴头流场动力学分析与结构优化[D].南京:南京林业大学,2009.

