一类非凸自治Hamilton系统的周期解

郑 波，邱俊雄

(广州大学数学与信息科学学院，广东广州 510006)

0 引言

考虑如下二阶离散Hamilton系统周期边值问题

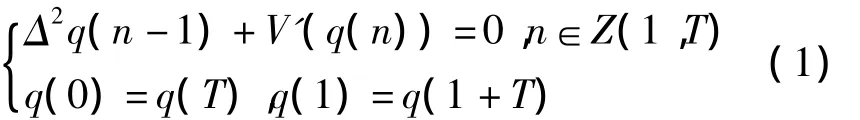
其中Δ是向前差分算子［1］，定义为 Δq(n)=q(n+1)－q(n)，Δ2q(n)= Δ(Δq(n))，V∈C2(RN，R)，V'(0)=0，T≥2 是给定的整数，Z(1，T)={1，2，3，…，T}.

早在2003年，临界点理论(包括极小极大方法与Morse理论等)就被成功地应用到差分方程边值问题和周期解的研究中［2］.自此，许多学者都开始应用临界点理论来研究差分系统解的存在性与多重性，获得了一系列有意义的结果［3－8］.对于具有变分结构的差分边值问题的研究，极小极大方法已经成为一个有力的工具.而临界点理论的另一个重要部分——Morse理论是更深刻、更精细的临界点理论，它在研究微分方程边值问题以及许多数学物理问题中已经发挥了巨大的作用.Morse理论应该仍然是讨论差分边值问题的重要的工具，但运用Morse理论来处理差分边值问题解的存在性与多重性的文献仍旧很少，主要难点在于精确计算离散系统中变分泛函临界点的临界群.本文将给出一系列条件以保证系统(1)对应的变分泛函J的临界点的临界群可比较，从而得到其非常值周期解的存在性定理.这是运用Morse理论讨论非凸自治Hamilton系统的非常数周期解的存在性的成功尝试.

关于差分方程的有关知识参见文献［1］.关于临界点理论的相关知识参见文献［9－10］.

1 主要结论

定理1 假设V∈C2(RN，R)，若:

(V1)V'(0)=0，V″(0)至少有一个特征值大于0;对于∀q≠0，V'(q)≠0;

(V2)存在C＞0，使V'(q)≤C，∀q∈RN;

(V3)V(q)→－∞，q→+∞，则系统(1)至少存在一个非常值T周期解.

为了证明定理1，需要下面一系列引理.

引理1 对∀k∈Z(0，T)且k≠0，k≠T，有

引理 2 对∀k，j∈，其中表示取其整数部分，则

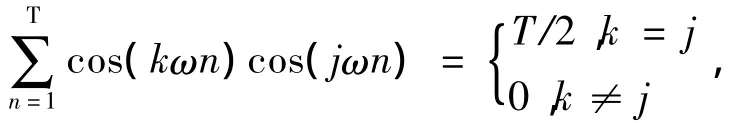
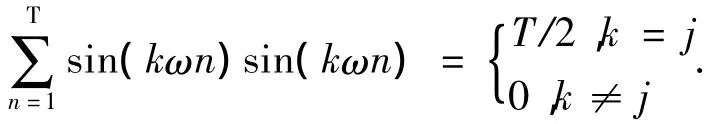
引理3 对∀q∈ET={q|q(n+T)=q(n)}，

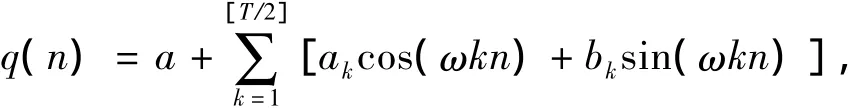
其中a，ak，bk是RN中常向量.

注:由引理3，

其中

从而，q(n)=a+u(n)并由引理1、2有0，并且有下列不等式成立.

引理4 (Wirtinger Type不等式)对任意的u∈Y，

现在，在ET上定义泛函:

其中Π为反差分算子，定义为

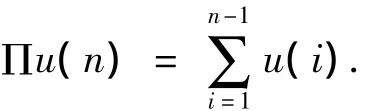
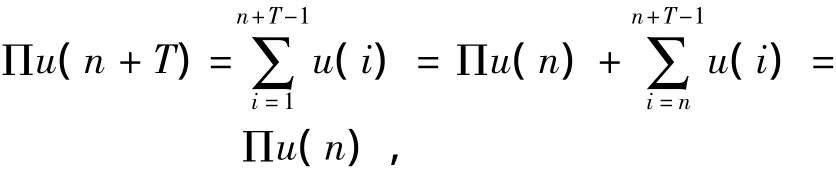
这意味着Πu(n)∈ET.

证明 注意到对任意的u，v∈ET有

通过直接计算并注意到Πu(n)∈ET，有:

也即

从而引理结论成立.

引理 6［9－10］设V∈C2(RN，R)满足(V2)、(V3)，则ψ在ET上满足Palais-Smale条件.即若{(uk，ak)}⊂ET，存在M＞ 0，对于 ∀k∈N，ψ(uk，ak)≤M且 ψ'(uk，ak)→0，k→∞，则{(uk，ak)}具有收敛子列.

证明 由ψ'(uk，ak)→0知存在K＞0，使当k＞K时有

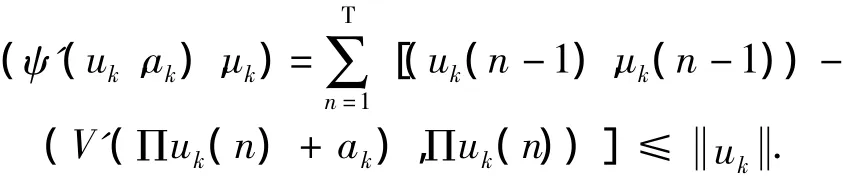
由(V2)及Wirtinger不等式 Πuk易知必存在C1＞0，使当k＞K时有

又由ψ(uk，ak)的有界性知存在C2＞0使得

由(2)，(V2)及 Wirtinger不等式知存在C3＞0，使，由(V3)即知存在C4＞0，使得

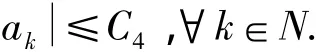
故{(uk，ak)}在ET有界，由于ET是有限维的，从而(PS)条件成立.

引理 7［9－10］设X是 Banach 空间，f∈C1(X，R)满足PS条件且有下界，则f必能达到极小值，即存在x0∈X，使f(x0)=infx∈Xf(x)，f'(x0)=0.

定义1［9－10］设()∈ET中ψ的临界点，令A(n)=V″(Π(n)+a).定义二次型:

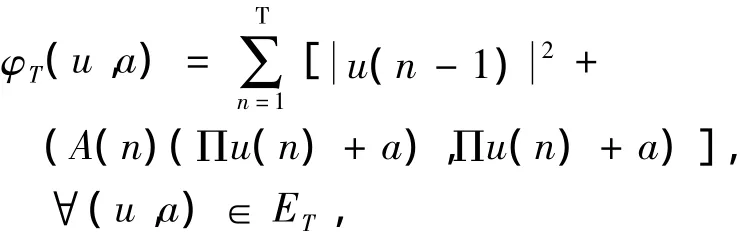
引理8 设a1≤a2≤…≤aN是V″(0)的特征值，则

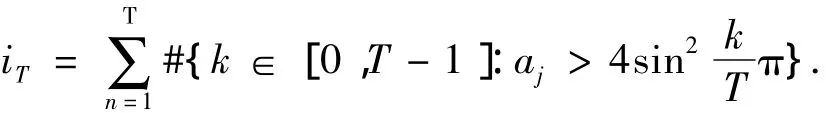
由引理8及条件(V1)即有:

引理9 ψ 在(0，0)的Morse指标iT(0，0)＞0.

2 主要结论的证明

有了上述的准备工作，现证明定理1.

定理1的证明 由(V3)知ψ(u，a)在ET上有下界，故由引理 7 知存在()∈ET，使 ψ()=inf(u，a)∈ETψ(u，a)且iT()=0.又由引理9知iT(0，0)＞0，故()≠(0，0).从而Π+必是(1)的非常值T周期解，若不然，Δ(Π+)=0 也即=0;而由()≠(0，0)，故≠0.由于Π+=是(1)的解，故V'()=0，这与假设∀q≠0，V'(q)≠0相矛盾，定理证毕.

［1］ AGARWAL R P.Difference equations and inequalities［M］.New York:Marcel Dekker，Inc，2000.

［2］ GUO Z，YU J.Existence of periodic and subharmonic solutions for second superlinear difference equations［J］.Sci China Ser A，2003，46:506-515.

［3］ AGARWAL R P，PERERA K，O'REGAN D.Multiple positive solutions of singular and nonsingular discrete problems via variational methods［J］.Nonlin Anal，2004，58(1/2):69-73.

［4］ ZHENG B.Multiple periodic solutions to nonlinear discrete Hamiltonian systems［J］.Adv Differ Equ，2007，Art.ID 41830，13.

［5］ ZHOU Z，YU J，GUO Z.Periodic solutions of higher-dimensional discrete systems［J］.Proc R Soc Lond Ser A Math Phys Engin Sci，2004，134:1013-1022.

［6］ ZHOU Z，YU J，CHEN Y.On the existence of gap solitons in a periodic discrete nonlinear Schrodinger equation with saturable nonlinearity［J］.Nonlinearity，2010，23(7):1727-1740.

［7］ ZHOU Z，YU J，CHEN Y.Periodic solutions of a 2nd-order nonlinear difference equation［J］.Sci China Math，2010，53(1):41-50.

［8］ SHI H.Boundary value problems of second order nonlinear functional difference equations［J］.J Differ Equ Appl，2010，16(9):1121-1130.

［9］ CHANG K C.Infinite dimensional Morse theory and multiple solution problems［M］.Boston:Birkhauser，1993.

［10］ MAWHIN J，WILLEM M.Critical point theory and hamiltonian systems［M］.New York:Springer-Verlag，1989.