一种自适应Z源升压变换器系统的仿真研究
高文根 黄德元 牛明强 李云飞
(1.安徽工程大学检测技术与节能装置省级实验室,安徽 芜湖 241000;2.芜湖奇瑞科技有限公司,安徽 芜湖 241000)
传统的升压变换器存在拓扑局限性,实际输出电压有限。为了解决这些不足,彭方正教授提出了基于Z源的升压变换器[1]。该Z源升压变换器在传统BOOST变换器的前端加上一个由电感电容组成的X型网络取代原有的电感,通过控制主开关导通比,此变换器在导通比小于0.5的时候就能达到理想的升压比。但目前对Z源直流变换电路拓扑的研究大部分局限于开环控制,在输入电压或负载发生变化时,此系统不能及时有效地做出调整,不能保证输出电压的稳定。
针对此问题,本次研究采用分段比例调节的控制方法,设计一种能自适应调节的闭环控制系统。这种控制策略能够在输入电压或负载发生变化时,保持输出电压稳定。通过Matlab软件进行了仿真验证实验,仿真结果证明了此方法的有效性。
1 主电路结构
基于Z源的自适应升压变换器系统拓扑结构如图1所示,由于Z源内部本身具有升压功能,所以该结构在开关管导通比相同的条件下,能够比传统的升压电路提供更高的输出电压。其中D1、D2的作用是使电流单向流动防止电流的反向灌流。导通比调节控制单元为整个系统的反馈控制单元,通过对输入输出电压的采样来计算开关管Q1的导通比,从而实现输出电压的稳定。
在Z源结构中L1和L2电压值很大且相等,C1和C2电压值很大且相等,有UL1=UL2=UL,UC1=UC2=UC。

图1 自适应Z源升压变换器拓扑结构
2 控制策略与仿真模型
采用分段比例调节控制策略的原理就是,由开关管导通比D和输入输出电压值Ui、Uo之间的关系式确定需要输出的额定直流电压,通过对输入和输出的电压进行实时采样,依据不同的条件对采样值进行分段处理计算,从而计算出能保持输出电压稳定的开关管导通占空比D。
设开关导通时间为DT,T为开关周期。由稳态电感磁通守恒规律可知,在一个开关周期内,电感两端电压平均值为0。可以得到:

其中UL为Z源电感两端电压,UC为Z源电容两端电压。
由式(1)、(2)可得:

由式(3)、(4)可得占空比D与输入输出电压Ui、Uo之间的关系为:

由式(5)得到D与Ui、Uo之间的关系,假设系统期望的稳定输出电压为U*o,纹波为γ,则分段函数为:

由式(6)可以构建出开关管导通比控制单元,当输出电压的纹波在误差范围之内,则利用期望稳定输出电压值U*o计算占空比D,否则采用输出电压采样值Uo计算占空比D。
采用Matlab构建分段比例调节控制单元模块如图2所示。用三角波作为载波,将通过计算得到的导通比D与之相加减,就可以构建出一个占空比可调的PWM波控制模块即分段比例调节控制单元,从而实现对Q1开关管的导通比调节。
期望稳定输出电压值为300 V,Z网络L1、L2的自感取3 mH,电容器C1、C2的电容取1 000 μF,搭建系统Matlab仿真模型结构如图3所示。

图2 分段比例调节控制单元模块

图3 系统仿真模型结构
3 仿真结果分析
仿真模型的期待稳定输出电压值为300 V,设定输出纹波为1%。保持负载不变,到达0.35 s时输入电压由100 V突变为120 V。传统Z源升压变换器输出电压波形如图4所示,到0.35 s时由于输入电压的增加,输出电压也随之发生波动,到达0.45 s恢复稳定到300 V,波动幅值较大。采用分段比例调节自适应控制后,输出电压波形如图5所示,输出电压到达0.35 s时发生波动,波动幅值较小,到0.4 s恢复稳定到300 V。

图4 输入电压突变时传统Z源升压变换器输出电压波形
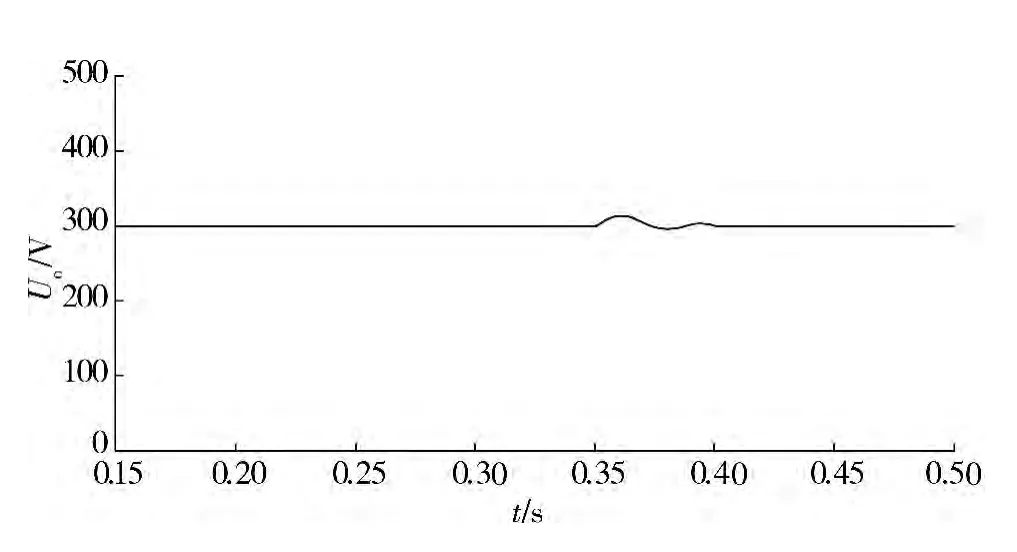
图5 输入电压突变时采用分段比例调节自适应控制Z源升压变换器输出电压波形
保持输入电压不变,到达0.35 s时系统的负载由100 Ω突变为40 Ω,传统Z源BOOST变换器输出电压波形如图6所示,到达0.35 s时负载突然增大,输出电压陡降,到达0.45 s之后开始趋于稳定。采用分段比例调节自适应控制后,输出电压波形如图7所示,输出电压因负载陡增所产生的波动较小,且在0.4 s即稳定保持期望输出电压300 V。
从以上仿真结果分析中可以看出,与传统Z源升压变换器比较,加入分段比例调节控制单元的自适应控制系统,在输入电压或负载突变时,输出电压波动幅度与恢复稳定时间都明显减小。因此,加入分段比例调节控制单元的自适应Z源升压变换器具有更好的稳定性,仿真结果表明本次控制策略设计达到预期目标。

图6 负载突变时传统Z源升压变换器输出电压波形

图7 负载突变时采用分段比例调节自适应控制Z源升压变换器输出电压波形
4 结语
本次研究采用分段比例调节控制策略,实现Z源升压变换控制系统能在输入电压或负载发生变化时进行自适应调节。通过Matlab搭建仿真模型,对控制策略实施仿真实验,结果验证了分段比例调节应用在Z源升压变换系统中的准确性和有效性。
[1]Peng F Z,Shen M S,Qian Z M.Maximum Boost Control of the Z-Source Inverter[G].IEEE Transactions on Power Electron,2005:833-838.
[2]Loh P C,Vilathgamuwa D,Gajanayake C J,et al.Transient Modeling and Analysis of Pulse-width Modulated zsource Inverter[G].IEEE Transactions on Power Electronics,2007:498-507.
[3]魏小敏,江明,高文根.Z源逆变器直流链升压电路控制方法研究[J].重庆科技学院学报(自然科学版),2012,14(6):136-139.
[4]袁啸林,江明,高文根,等.基于Z源变化器的直流无刷电动机驱动系统研究[J].安徽工程大学学报,2012,27(1):50-52.
[5]Liu J,Hu J,Xu L.Dynamic Modeling and Analysis of Z-source Converter-derivation of Ac Small Signal Model and Design-oriented Analysis[G].IEEE Transactions on Power Electronics,2007:1786-1796.
[6]Bash M,Chan R R,Crider J,et al.A Medium Voltage DC Testbed for Ship Power System Research[G].IEEE Electric Ship Technologies Symposium,2009:560-567.
[7]Shen M,Joseph A,Wang J,et al.Comparison of Traditional Inverters and Z-Source Inverter for Fuel Cell Vehicles[G].IEEE Transactions on Power Electronics,2007:1453-1463.
[8]王利民,钱照明,彭方正.Z源升压变换器[J].电气传动,2006,36(1):28-32.

