一类分数阶混沌系统的投影同步研究
孔德富,赵小山
(天津职业技术师范大学理学院,天津300222)
一类分数阶混沌系统的投影同步研究
孔德富,赵小山
(天津职业技术师范大学理学院,天津300222)
其中x,y,z为系统(3)的状态变量,a,b,c为系统的参数,0<qi<1,qi为系统的阶数(i=1,2,3).当a=10,b=
针对一个三维分数阶混沌系统,分析了其动力学混沌行为,基于分数阶稳定性原理,设计合适的控制器,并利用Laplace变换实现了该系统的混沌投影同步.最后,借助数值仿真,验证了该结论的有效性和正确性.
分数阶混沌系统;投影同步;控制器
0 引言
近十几年来,分数阶微积分理论由于在松弛、震荡、湍流等方面表现出比整数阶更突出、更诱人的前景,成为当前研究热点[1-3].自1990年,Pecora和Corroll首次在电路实验中提出驱动—响应法,成功实现耦合混沌系统同步以来[4],学者相继提出不同的混沌同步方法,如主动—被动同步分解法[5]、耦合控制法[6]、广义同步法[7]、神经网络同步法[8]等.随着研究的深入,学者们实现了不同类型的混沌同步,有完全同步、广义同步、投影同步等[9-11].笔者分析了一个三维分数阶混沌系统,通过设计控制器,利用Laplace变换实现了该系统的投影同步,数值模拟验证了该方法的有效性和正确性.
1 分数阶混沌系统平衡点及其稳定性分析
分数阶微积分的定义形式多样,本文用的是Caputo定义[12],即:

1)式中m=[α],Jθ是θ阶Riemann-Liouville积分算子,它被定义为

其中Г(·)是Gamma函数.

文献[13]提出了一种三维自治混沌系统所对应的分数阶混沌系统:3,c=17时,可解得该系统有3个平衡点若设系统的平衡点表示为则该系统的Jacobian矩阵为:

由(4)式可得特征方程为:
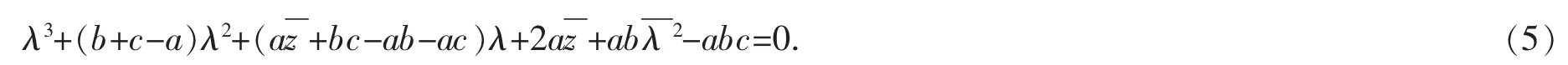
定理1[14,15]若Jacobian矩阵的特征根满足

则系统在平衡点是渐近稳定的.
(1)在平衡点s0=(0,0,0)处的特征多项式(5)变为

解得(7)的特征值为λ1=10,λ2=-17,λ3=-3.
根据定理,由于存在正实根λ1=10,所以平衡点s0=(0,0,0)不稳定.

解得(8)的特征值为λ1=8.513 5+20.216 5i,λ2=8.513 5-20.216 5i,λ3=-27.026 9.
第3个根是负根,而第1和第2个特征值的幅角为|arg(λ1,2)|=66.3°,因此根据定理,只要α>0.74,此时平
衡点s1是不稳定的平衡点.
利用Matlab仿真得到当q1=q2=q3=0.9时,其混沌吸引子如图1所示,通过观察各个相平面的吸引子图,可以清晰地看到该混沌吸引子是双漩涡结构.
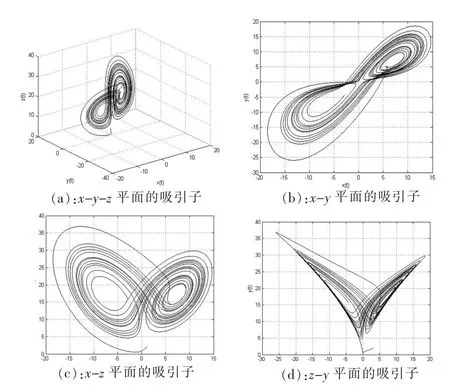
图1 系统(3)的混沌吸引子
2 投影同步与数值仿真
2.1 投影同步
定理2设驱动系统为Dαx(t)=F(x),响应系统为Dαy(t)=G(y),x=(x1,x2,…,xn)T∈Rn,y=(y1,y2,…,yn)T∈Rn为相应的状态变量.定义同步误差为:

其中e=(e1,e2,…,en)T,ei=yi-αxi(i=1,2,…,n),α称为比例因子.若存在1个常数α(α≠0)使得则称驱动系统和响应系统之间实现了投影同步.
2.2 分数阶混沌系统的投影同步
设驱动系统为

响应系统为

其中u1(t),u2(t),u3(t)为系统同步控制变量.
定理3其投影同步误差设为e1=y1-αx1,e2=y2-αx2,e3=y3-αx3,其中α为投影同步比例因子.令控制器为:

则驱动系统(10)和响应系统(11)达到同步.
证明由驱动系统(10)和响应系统(11)计算得到误差系统为:

接下来对(13)式两边求Laplace变换,则令:E1(s)=L(e1(t)),E2(s)=L(e2(t)),E3(s)=L(e3(t)),并利用可以得到:

由(14)式计算得:

根据Laplace变换理论终值定理,有:

假设E1(s),E2(s),E3(s)均有限,那么可得这证明驱动系统(10)和响应系统(11)达到同步.
2.3 数值仿真
根据预估-校正算法,通过数值仿真来验证所设计方法的正确性.选取系统的阶数q1=q2=q3=0.9,驱动系统(10)的初始值(x1(0),x2(0),x3(0))=(1,3,2),响应系统(11)的初始值(y1(0),y2(0),y3(0))=(1,2,-0.1),投影比例因子α=0.3,得到误差系统的时间历程图如图2所示,可以观察到随着时间t的增长,各条误差曲线快速的趋于0,即:驱动系统和响应系统通过投影同步控制实现了自结构同步.
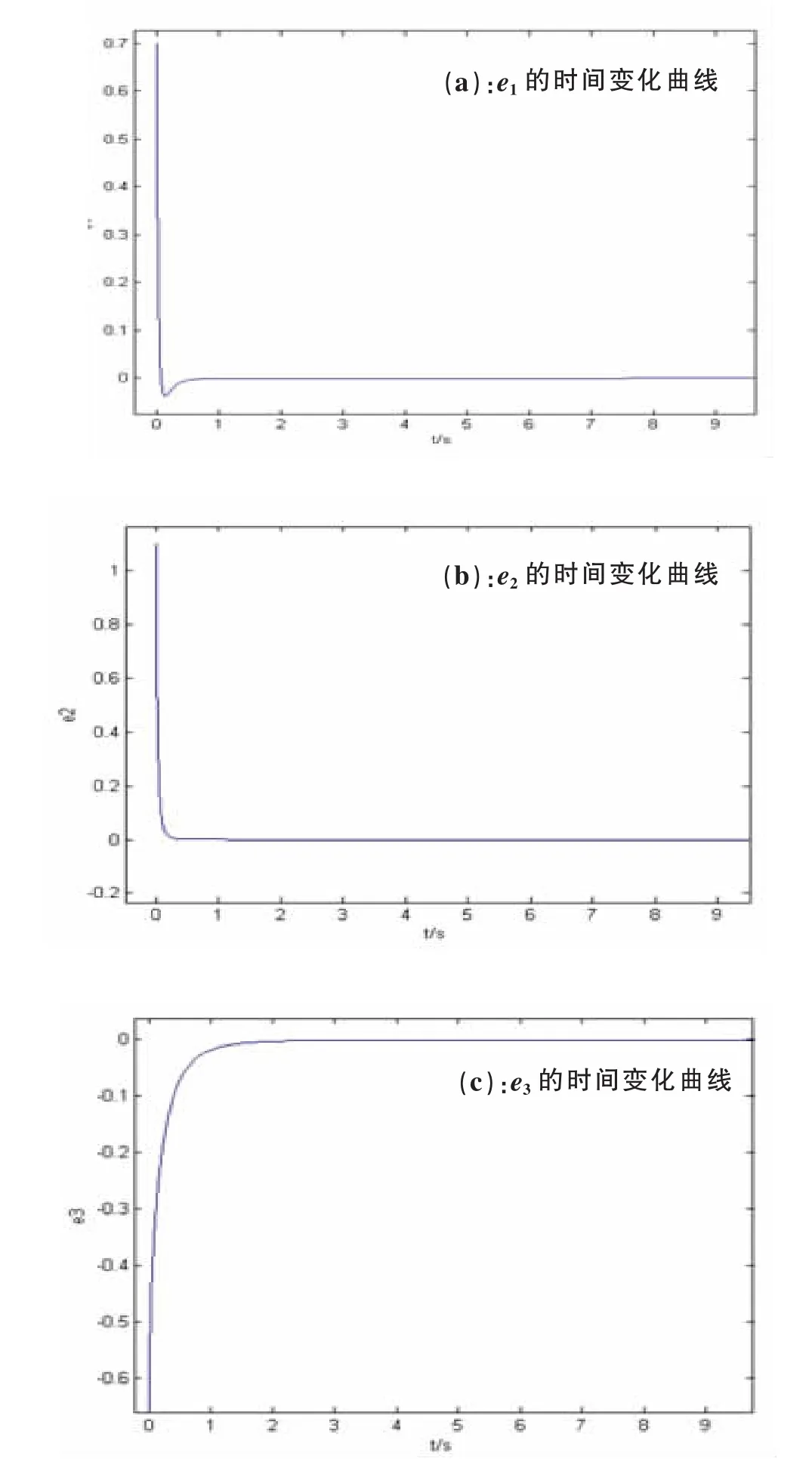
图2 误差系统(13)的时间历程图
3 结论
针对一个三维分数阶混沌系统,基于分数阶稳定性理论,计算了该系统的平衡点,分析了该系统在平衡点的稳定性;随后,设计了合理的投影同步控制器,利用Laplace变换给予严格证明,最后数值仿真验证其正确性.
[1]ORTIGUEIRAMD,MATORSCJ,PIEDADEMS.FractionalDiscretetimeSignalProcessing:ScaleConversionandLinearPrediction[J]. NonlinearDynamics,2002,29(1):173-190.
[2]BAREENAR,DELASENM.OntheSufficientlySmallSamplingPeriodfortheConvenientTuningofFractionalOrderHoldCircuit[J].IEE Proceedings:ControlTheoryandApplications,2003,150(2):183-188.
[3]ICHISEM,NAGAYANAGIY,KOJIMAT.AnAnalogSimulationofNon-integerOrderTransferFunctionsfor Analysis of Electrode Processes[J].JournalofElectroanalyticalChemistry,1971,33(2):253-265.
[4]PEEORALM,CARROLLTL.SynchronizationinChaoticSystems[J].PhysicalReviewLetters,1900,64(8):821-827.
[5]PARLITZU,ERGZINGERS.RobustCommunicationBasedChaoticSpreadingSequence[J].PhysicsLettA,1994,188(1):146-150.
[6]JIANGGP,TANGWK-S,CHENGD.ASimpleGlobalSynchronizationCriterionforCoupledChaoticSystemsChaos[J].ChaosSoliton Fract,2003,15:925-935.
[7]SHANLiang,LIJun,WANGZhiquan.GeneralizedSynchronizationofUnifiedChaoticSystemandtheResearchofCSK[C].Proceedings ofthe8thICARV.Washington:IEEEComputerSociety,2004:1928-1933.
[8]MAWei,WANGZhengou.ANewChaoticParametersDisturbanceNeuralNetworkforSolvingGlobalOptimizationProblems[J].CommunicationsinTheoreticalPhysics,2003,39(4):385-392
[9]董俊,张广军,姚宏.异结构超混沌系统的完全同步与反相同步控制[J].空军工程大学学报,2012,13(5):90-94.
[10]王兴元,孟娟.一类混沌神经网络的观测器广义投影同步设计[J].应用力学学报,2008,25(4):656-659.
[11]MAINIERI R,REHACEK J.Projective Synchronization in Three-dimensional Chaotic System[J].Physical Review Letters,1999,82(15):3042-3045.
[12]PodlubnyI.FractionalDifferentialEquations[M].NewYork:AcademicPress,1999.
[13]徐强,包伯成,胡文,等.分数阶混沌系统数值解析与电路仿真研究[J].计算机应用研究,2010,27(12):4612-4614.
[14]MATIGNON D.Stability Results for Fractional Differential Equations with Application to Control Processing[J].Computational EngineeringinSystemsandApplicationMulticonference,1996,2:963-968.
[15]AHMED E,EL-SAYED A M A,ELSAKA H A A.Equilibrium Points,Stability and Numerical Solutions of Fractional-order PredatorpreyandRabiesModels[J].JMathAnalAppl,2007,325(1):542-553.
(责任编辑 钮效鹍)
Projective Synchronization Study of Fractional Order Chaotic Systems
KONG De-fu,ZHAO Xiao-shan
(School of Science,Tianjin University of Technology&Education,Tianjin 300222,China)
In view of a three-dimensional fractional order chaotic system,this paper analyzes its chaos dynamic behavior.A reasonable controller is designed by using the fractional stability theory.The problem of projective synchronization of the chaotic system is investigated based on the Laplace transform.At last,numerical simulations are used to illustrate the effectiveness and correctness of proposed synchronization method.
fractional order chaotic system;projective synchronization;controller
TP273
:A
:1673-1972(2015)06-0033-05
2015-06-03
国家自然科学基金(11302158;11302148);天津职业技术师范大学研究生创新基金(YC14-14)
孔德富(1988-),男,河北邯郸人,硕士研究生,主要从事非线性动力系统混沌同步研究.

