基于无单元法的水力劈裂数值模拟计算

张 鑫

近年来，诸如无单元法、边界元法、非连续变形分析（DDA）等更适用于解决大变形及裂纹扩展等问题的数值计算方法的快速发展，为更好地解决水力劈裂等问题提供了有力的数值计算工具。本文利用损伤力学的相关概念，并基于无单元法建立起应力-渗流-损伤三场耦合数值计算模型，充分发挥了无单元法在追踪裂纹扩展方面的优势。的关系为：岩体处于弹性状态时，材料未发生破坏，损伤变量D=0，渗透系数和有效应力为负指数关系。当应力大于材料的抗拉强度时，裂纹开裂，材料发生破坏，此时 0＜D＜1，引入渗透系数增大系数，材料渗透性有所提高，当材料发生破坏时，D=1，渗透系数将会大幅增大。

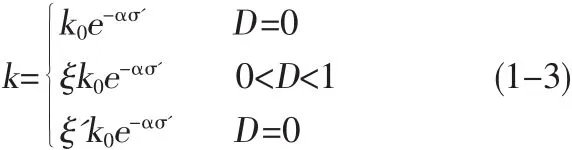
1. 计算方法

根据损伤力学的相关理论，材料受损伤前后弹性模量是变化的，并认为无损材料的应变与全应力作用于受损材料产生的应变是等价的。根据这一假定，引入损伤变量，将受损材料的弹性模量定义为

式中E，为产生裂纹材料的弹性模量；E为未产生裂纹材料的弹性模量。D为损伤变量，D=0表示材料处于无损伤状态，D=1表示材料处于完全损伤（断裂或者破坏）状态，0＜D＜1对应不同的损伤程度。

岩体等材料的拉应力大于其抗拉强度时，材料的损伤变量为

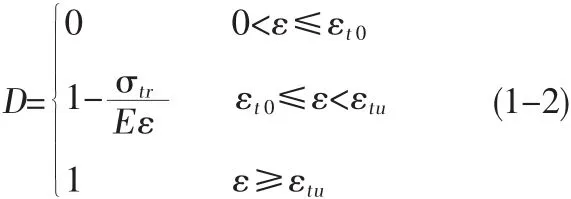
式中，σcr为材料损伤后的残余强度；E意义同上。

岩体材料的渗透系数和其应力状态存在一定的关联，主要表现在随着岩体应力的增大，当其裂尖材料的应力大于抗拉强度时，岩体开始破坏，裂纹开始扩展，裂纹的开度随之增加，裂隙间材料的渗透性增加，相应结点的渗透系数将会增大；相反，若裂纹闭合或其未扩展，材料未损伤，相应区域材料的渗透系数不增大，其数值和有效应力仍为负指数关系。根据以上原理，建立应力和渗透系数

式中，ξ为渗透系数增大系数。

基于以上原理建立应力-渗流-损伤耦合计算模型，并编制相关计算程序。

2. 注意事项

渗流场、应力场以及损伤场3场耦合关系十分复杂，需要各自考虑的边界条件也不尽相同，得到解析解是十分困难的。本文分别计算3场，并利用3场之间的相互耦合关系进行迭代循环，以达到它们的动态平衡，以满足计算精度作为迭代计算终止条件。

3. 算例分析

如图1所示，建立岩体二维平面应力模型，边界条件为：水平方向两侧围压4MPa，竖直方向顶端水压力 2.3MPa（向下），底端水压力 3.8MPa（向上）；岩体的弹性模量10GPa，岩体渗透系数为 1.0×10-6m/s，抗拉强度 10MPa，残余抗拉强度0.1MPa，抗压强度 100MPa，残余抗压强度10MPa。岩体二维计算模型和无单元模型高斯点分布如图1所示，其中初始裂纹与底边的夹角为58°。分别对不考虑损伤和考虑损伤2种情况进行对比计算分析。

图1平面应力模型示意图

图2不考虑损伤变量流速矢量分布图

图3考虑损伤变量流速矢量分布图

通过对比图2和图3考虑及不考虑损伤时流速矢量分布图可以看出，考虑损伤作用后，在裂纹扩展的部分区域的损伤变量达到了材料的抗拉和抗压强度，岩体发生了破坏，裂纹体内部裂隙的连通性有所提高，使得裂纹计算区域的渗透系数有了较大幅度的增加，相关区域内的渗透流速矢量较之未考虑损伤作用时亦有所增大。此外，在考虑损伤作用后，沿裂纹走向以及裂尖的部分区域的应力值较未考虑损伤作用时应力值偏小。这主要是由于在迭代计算过程中，裂纹计算区域的应力达到了材料的损伤阙值，材料产生了不同程度的损伤，相关高斯计算点附近的材料强度按照弹脆性损伤本构方程式进行了刚度退化处理，故其应力有所降低。

在模拟水力劈裂的数值模型中加入损伤变量，考虑其对于岩体渗透系数和岩体刚度的影响后得出的结论。

无单元法作为新兴的计算方法，摆脱了网格划分的局限，在水力劈裂数值模拟计算过程中可以随着裂纹的扩展在裂尖位置随意增加结点，较传统的有限元法其在处理大变形及裂纹扩展等问题方面具有明显的优势。无单元法模拟分析了含有裂缝的岩体的破裂过程。通过对比计算表明，考虑了损伤变量对于水力劈裂过程中的渗流场特性和应力分布影响的计算结果与文献的实验结果更为接近。因此，耦合模型可以用来研究岩体的破裂或水力劈裂，具有理论意义和应用价值。