低信噪比下时频联合的载波同步算法

孙锦华,韩会梅

(西安电子科技大学综合业务网理论及关键技术国家重点实验室,710071,西安)



低信噪比下时频联合的载波同步算法

孙锦华,韩会梅

(西安电子科技大学综合业务网理论及关键技术国家重点实验室,710071,西安)

针对短突发通信在低信噪比下编码辅助同步算法存在估计精度低和同步范围小的问题,提出了一种时频联合的载波同步(JTDFDCY)算法。首先采用频域估计算法、时域估计算法和最大似然(ML)算法对导频信号进行处理,得到频率粗估计值和相位粗估计值;然后用频率粗估计值和相位粗估计值对接收信号进行补偿,并对补偿后的信号进行解调解码、重新编码、基带调制,得到软判决符号;最后采用时域相关和算法和ML算法对软判决符号进行处理,得到频率细估计值和相位细估计值,进而实现有效的载波同步。仿真结果表明: JTDFDCY算法在低信噪比下的粗估计能够兼顾频率估计范围和估计均方根误差的要求;当归一化频偏在(-0.5,0.5)范围时,仅利用6.1%的导频开销即可将系统的性能损失控制在0.1 dB以内。

低信噪比;导频;载波同步;编码辅助

在高速移动通信、深空通信和卫星通信中,接收机长时间在低信噪比下工作,由于通信双方的相对运动,接收信号总是存在较大的多普勒频偏[1]。为使采用Turbo码、Turbo乘积码(TPC)和低密度奇偶校验码(LDPC)[2-3]等的短突发系统在低信噪比下正常工作,有效的载波同步是需要解决的关键问题。近年来,针对现有的开环载波参数估计方案的缺陷,研究者陆续提出了一些频偏估计方法[4-7],但这些方法的估计范围提升有限或工作信噪比门限较高。码辅助的同步算法[8-15]利用香农极限码的特点,将译码和同步相结合,显著提高了算法的估计性能。联合导频和迭代译码软信息的ML-ITDD算法[8]能够校正小于7×10-4的归一化频偏,但是由于采用最大似然(ML)准则进行频率搜索,算法比较复杂。非数据辅助迭代载波同步算法[10]能校正大范围的载波频偏和相偏,获得接近理想的误比特性能,但算法采用频相二维搜索,复杂度非常高。文献[13]针对LDPC系统提出导频与编码联合辅助的同步算法,但在归一化频偏大于3×10-4时与理想性能相差较大。文献[14]针对Turbo系统提出联合导频和迭代译码的同步算法,但在归一化频偏大于1.5×10-3时与理想性能相差较大。文献[15]提出的联合旋转平均周期图和解调软信息载波估计算法,频偏估计范围可达符号速率的一半,但细估计采用了分段的频相二维搜索,复杂度稍高。

针对上述问题,在文献[14-15]的基础上,本文提出了一种时频联合的载波同步算法(JTDFDCY)。该算法首先采用频域旋转平均周期图(rotational periodogram averaging, RPA)算法、时域相关和算法和ML算法,对导频信号进行处理得到频率粗估计值和相位粗估计值,然后用频率和相位的粗估计值对接收信号进行补偿,并对补偿后的信号进行解调解码、重新编码、基带调制,得到软判决符号,最后采用时域相关和算法和ML算法对软判决符号进行处理得到频率细估计值和相位细估计值,进而实现有效的载波同步。由于频域旋转平均周期图算法的估计范围可以达到符号速率的一半,时域相关和算法和ML算法的估计精度较高,因此本文所提出的算法具有估计范围大、估计精度高的特点。仿真结果表明,在低信噪比条件下,本文算法能够兼顾频率估计范围和估计精度的要求;当归一化频偏在(-0.5,0.5)范围时,仅利用6.1%的导频开销就能将系统的性能损失控制在0.1 dB以内。另外,本文算法的复杂度较小,有利于工程应用。

1 系统模型

首先将信息序列编码,将导频序列平均分成前后两段,与编码后的数据复用组成一个数据帧结构。整个数据帧长为N个符号,前段导频和后段导频长度均为Lp(Lp为两段导频间的符号个数),两段导频之间的数据符号长度为L1,后段导频之后的数据符号长度为L2,两段导频的符号间距为D=Lp+L1,细估计用到的数据符号长度为L3,数据帧结构如图1所示。该数据帧经过调制得到复基带信号,通过高斯白噪声信道,附加载波频偏和相偏。接收到的等效离散基带信号可以表示为

rk=skexp(j(2πΔfkT+φ))+nk,

k=1,2,…,N

(1)

图1 数据帧结构

在接收端,接收信号首先被送到解复用器,提取出导频序列进行载波粗估计,再用频率和相位的粗估值对接收信号进行补偿;然后将补偿后的信号送至解调器和译码器,译码器输出的信息序列经过编码、基带调制送至细估计器进行载波细估计,再用粗估计和细估计的频率和相位值对接收信号进行补偿;最后对补偿后的信号进行解调译码即可恢复出信息序列。上述系统同步模型如图2所示。

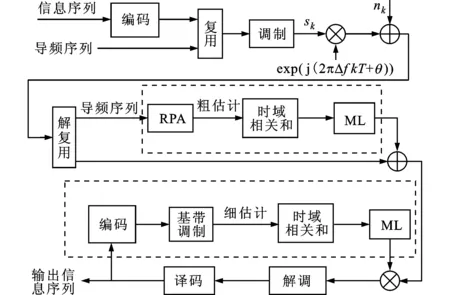
图2 系统同步模型

2 载波同步算法

2.1 导频辅助的载波粗估计

在低信噪比下,为了保证经过粗同步后的码字在含有剩余频偏时软信息的可靠性,本算法的粗估计采取了频域和时域相结合的算法,利用频域旋转平均周期图算法和时域相关和算法进行频率粗估计,用ML算法进行相位粗估计。另外,用先进的数字信号处理器[16]可以实现对载波频差和相差的实时捕获。

2.1.1RPA算法 将接收到的基带信号通过解复用进行信号分离,提取出接收信号中的前段导频,并计算去调制信号

(2)

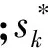
(3)

式中:angle表示求幅角。将fRPA与fsc相加,得到频偏粗估计值fco。

2.1.3 ML算法估计载波相位 利用前段导频通过最大似然算法计算相偏粗估计值

(4)

2.2 编码辅助的载波细估计

用载波粗估计值对接收信号进行校正,得到校正信号

,

k=1,2,…,N

(5)

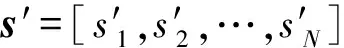
(6)

这里需要说明的是,如果系统采用PSK或QAM调制方式,也可以通过非线性判决的方法得到软判决符号s′。研究表明,在译码器的后验概率对数似然比可靠性较高时,这两种方法得到的软判决符号s′是近似等价的[16]。

通过时域相关和算法得到频偏细估计值

(7)

通过ML算法计算相偏细估计值

(8)

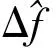
3 参数设置及仿真分析

本文细估计的码辅助同步算法利用的是经过解码、再重新编码、基带调制的软判决符号,跟纠错码的类型及调制方式无关,因此本文同步算法参数的选择不受纠错码、调制方式的影响。本文同步算法参数的取值需要根据系统的误比特性能要求以及编码调制方式来确定。由于TPC码在比较高的编码速率和码长较短的情况下仍可以获得非常好的纠错能力,且译码复杂度较低,因此具有恒包络特性的SOQPSK信号具有良好的频谱利用率和功率利用率,非常适合应用于短突发传输系统。下面以TPC编码加SOQPSK调制为例,给出本文算法中各参数的设置及仿真结果。系统中各信号参数如下:TPC子码为(32,26)扩展汉明码,编码数据共12个TPC块,调制方式为MIL SOQPSK调制。相偏为均值为[-π,π)、方差为5°的高斯随机变量。

3.1 算法中各参数的设置及分析

由于频偏随时间的积累会对数据产生严重的影响,进而影响系统的误比特性能,因此对于给定长度的数据应首先由归一化频偏对系统误比特性能的影响确定粗估计算法和细估计算法应达到的归一化均方根误差(eRMS)。由于时域相关和算法的均方根误差由相关长度决定,因此细估计阶段的相关长度L3应由细估计算法应达到的eRMS确定。粗估计阶段RPA算法的eRMS应在粗估计时域相关和算法的估计范围内,而粗估计时域相关和算法的估计范围由两段导频的间距D确定,D越大,估计范围越小,估计的eRMS也越小。粗估计时域相关和算法的估计范围越小,会对RPA算法的eRMS提出较高要求。为了降低RPA算法的均方根误差,必须增大导频开销。因此在粗估计参数的设计中,为了减小导频开销,可以选择稍小的导频间距,使得有限导频开销导致RPA算法eRMS较大的缺陷可以由时域相关和算法进一步弥补,这样经过三级同步保证以最小的导频开销获得最终所要求的估计精度。

3.1.1 确定粗估计算法及及细估计算法应达到的eRMS图3给出了不同归一化频偏ΔfT对系统误比特率性能的影响。从图中可以看出,ΔfT越大,对系统的误比特率影响越大。当ΔfT<5×10-6时对系统误比特率的影响较小,因此粗估计频率的eRMS应达到5×10-6。当要求系统的误比特率性能损失为0.1 dB时,细估计频率的eRMS应达到2×10-6。

图3 不同归一化频偏对系统误比特率性能的影响

3.1.2 确定两块导频之间的数据符号长度L1L1的实质就是两块导频之间所包含的符号个数。图4给出了Eb/N0=1 dB时L1对本文粗估计频率的eRMS的影响。从图4可以看出,当L1不小于1 026时,本文粗估计频率的eRMS不大于5×10-6。为了既能控制导频开销又能保证本文粗估计频率的eRMS约为5×10-6,设置L1=1 026。

图4 两块导频之间的距离对本文粗估计算法的影响

3.1.3 确定导频符号数Lp图5给出了Eb/N0=4 dB时,Lp对RPA算法的eRMS的影响。RPA算法估计频率的eRMS应在时域相关和算法的估计范围内,因此需要首先求出粗同步时域相关和算法的估计范围1/2(Lp+L1)[14],当Lp小于200,L1=1 026时,1/2(Lp+L1)在4×10-4量级。从图5中可以看出,当Lp大于100时,RPA算法估计频率的eRMS均能落在时域相关和算法的估计范围内。但是,图5中的eRMS是实验统计的平均值,如果某一次RPA算法估计频率的eRMS超出或接近粗同步时域相关和算法的估计范围,则会造成粗估计性能的恶化,因此需要进一步由RPA算法估计频率的eRMS的统计特性来确定合适的导频数。对估计频率的eRMS的统计比较耗时,而且也没有必要对较大Lp进行测试,因此本文选择几个离散点进行测试。表1给出了Lp为157和200时进行10 000次仿真的RPA算法粗估计频率eRMS的统计结果。可以看出,Lp为157和200时RPA算法的eRMS均小于4×10-4,但Lp=157比Lp=200的eRMS有更大的概率落在[2×10-4,4×10-4]区间,因此选取Lp=200。此时导频开销为2Lp/(2Lp+12×513)=6.1%,其中每个TPC块的符号数为513。

表1 RPA算法在不同eRMS范围内的统计结果

图5 Lp对RPA算法估计频率均方根误差的影响

3.1.4 确定频偏旋转因子M和FFT变换点数NF首先固定FFT变换点数,确定频偏旋转因子。当Lp=200、NF为512点时,RPA算法的粗同步频率估计性能与载波频率位置关系的曲线如图6所示。由于频偏旋转相当于对FFT两根谱线中间不能分辨的频率范围进行谱分析,并且分析结果关于两根谱线的中心是对称的,因此图中只画出了FFT量化频率点从n到n+0.5的估计性能。从图中可以看出,当M=16时,RPA算法的估计频率eRMS小于4×10-4,并且幅度波动较小,因此旋转因子选取M=16。确定了频偏旋转因子后,再根据RPA算法的估计频率eRMS统计结果来确定适当的FFT点数m。在Eb/N0=3.75 dB、m=(1,2,…,10)×512时,统计了10 000次RPA算法的估计频率的最大eRMS,当FFT点数大于等于1 024时,最大eRMS均小于4×10-4,考虑到实际工程应用,选择FFT点数为1 024。

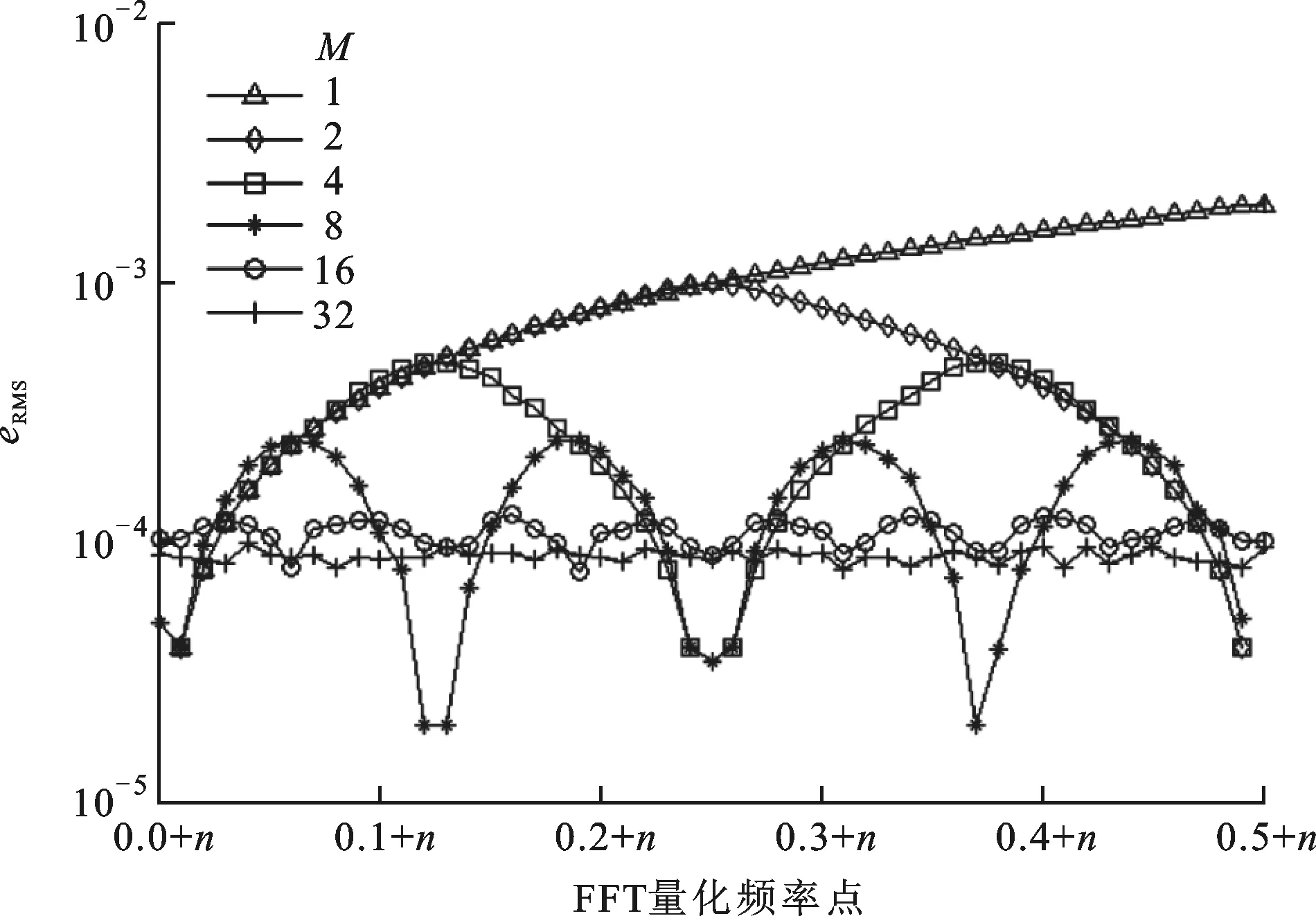
图6 粗同步频域估计性能与载波频率位置的关系

3.1.5 确定数据符号数 图7给出了数据符号数L3对细估计频率eRMS的影响。从图7中可以看出,当L3不小于3 791时,细估计频率的eRMS不大于2×10-6。由3.1.1节可知,当细估计频率的eRMS为2.0×10-6时,系统误比特率损失为0.1 dB。由于L3越长,细估计频率的eRMS越小,因此为了达到理想的载波同步,细估计中采用的L3=4 304。

图7 L3对细估计频率均方根误差的影响

3.2 误比特性能

图8 时频联合载波同步算法在较大频偏下的误比特性能

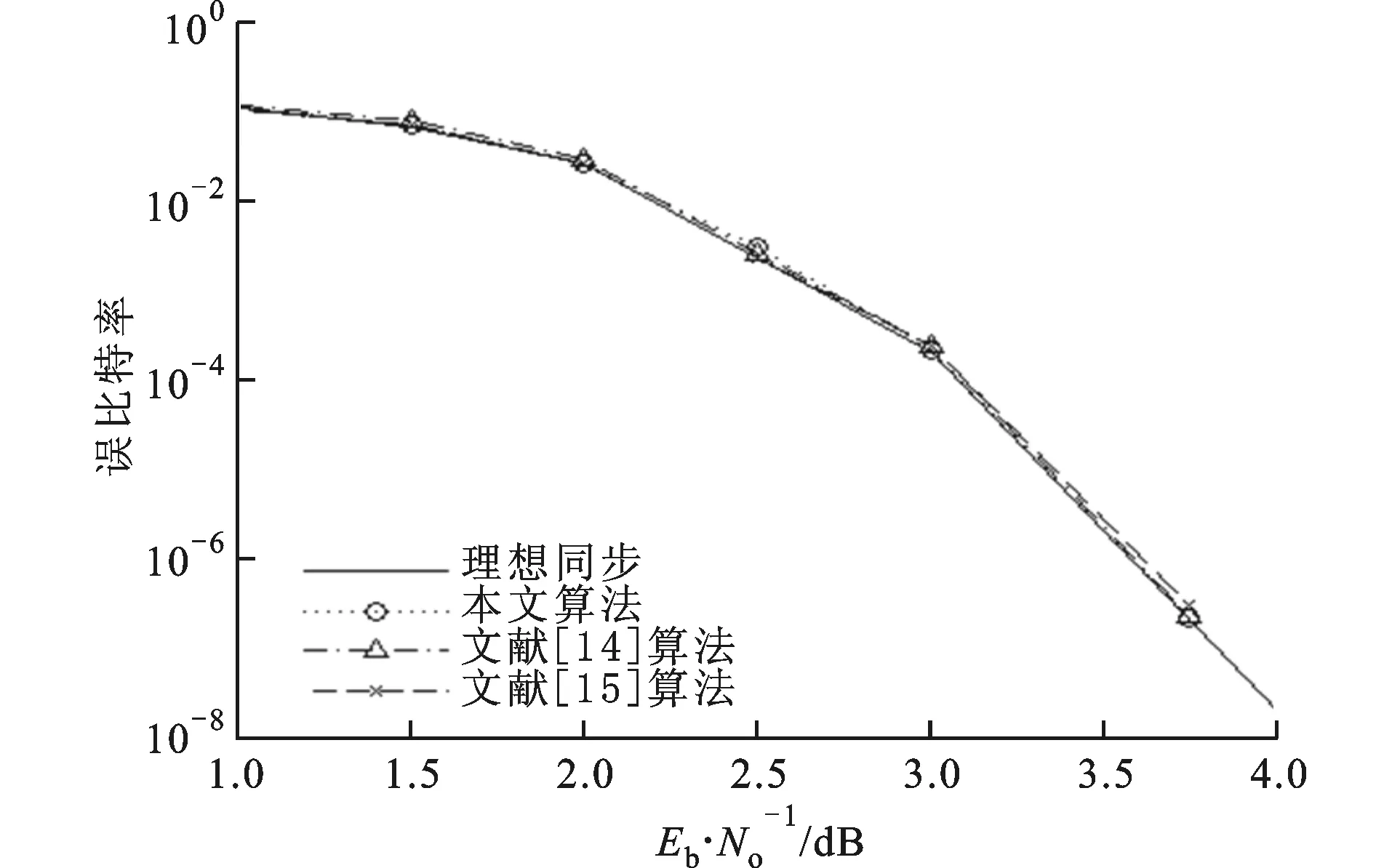
图9 时频联合载波同步算法在较小频偏下的误比特性能

图8和图9分别给出了归一化频偏ΔfT为0.45和1×10-4时本文算法和文献[14-15]中同步算法的误比特率曲线和理想曲线比较。可以看出,无论是在大归一化频偏(ΔfT=0.45)或是小归一化频偏(ΔfT=1×10-4)下,本文和文献[15]的算法均能有效的估计并校正载波偏差,获得几乎接近理想同步的误比特性能,但文献[15]算法的复杂度过高,不利于实际应用,而文献[14]算法的频率估计范围仅为|ΔfT|<1.5×10-3,在这个估计范围内,如ΔfT=1×10-4时,能有效地估计并获得接近理想同步的误比特性能,若超出此估计范围,如ΔfT=0.45时,误比特性能会严重恶化。

3.3 算法复杂度

表2给出了本文算法与文献[14-15]算法的复杂度,主要列出了算法步骤中的乘法和加法运算次数,并忽略几种算法共同需要的去调制、求最大值、求幅角的运算量,其中v表示译码迭代次数(Turbo码一般取5～8次,TPC一般取4～6次),S是非数

据辅助盲搜索算法的搜索次数(文献[15]中S大约为几十次)。为便于比较,将3Lp点的DFT的运算量(实际采用FFT的运算量更小)作为文献[15]和本文算法中RPA算法运算量。在粗估计阶段,文献[14]算法的复杂度最小,文献[15]和本文算法的复杂度相当。在细估计阶段,文献[14]的算法需要在译码迭代中更新载波参数估计值从而导致算法的复杂度较高,文献[15]的频率搜索也会导致算法的复杂度较高,而本文基于时域相关和的方法则大大降低了运算复杂度。

表2 3种算法的复杂度比较

4 结 论

针对短突发通信在低信噪比下编码辅助同步算法存在的估计精度低和同步范围小的问题,提出了一种时频联合的载波同步算法,能够获得较高的估计精度和较大的估计范围。本文算法的编码辅助只用到译码的输出结果,而不需要译码过程中的信息,因此不用考虑码的特定结构,具有普遍适用性。只要本文算法中的各参数设置合理,就能达到理想的载波同步,另外本文算法具有较小的复杂度,更加适合应用在短突发通信系统中。

[1] FARR W. Technology development for high efficiency optical communication [C]∥Proceedings of IEEE Aerospace Conference. Piscataway, NJ, USA: IEEE, 2012: 1-8.

[2] BERROU C, GLAVIEUX A, THITIMAJSHIMA P. Near Shannon limit error-correcting coding and decoding: turbo-codes [J]. IEEE Transactions on Communications, 1996, 44(10): 1261-1271.

[3] 孙锦华, 李梦良, 吴小钧. 连续相位调制和Turbo乘积码的串行级联系统设计 [J]. 西安交通大学学报, 2012, 46(4): 88-93. SUN Jinhua, LI Mengliang, WU Xiaojun. The design of serial concatenated system of Turbo product code with continuous phase modulation [J]. Journal of Xi’an Jiaotong University, 2012, 46(4): 88-93.

[4] 张毅, 欧阳志新, 邓云凯, 等. 高性能无数据辅助QPSK频偏估计新算法 [J]. 西安电子科技大学学报, 2013, 40(2): 187-193. ZHANG Yi, OUYANG Zhixin, DENG Yunkai, et al. New high performance non-data-aided frequency estimation and implementation of QPSK [J]. Journal of Xidian University, 2013, 40(2): 187-193.

[5] 张帅, 张晓林. 数字电视大范围载波频偏快速捕获算法 [J]. 北京航空航天大学学报, 2013, 39(2): 225-229. ZHANG Shuai, ZHANG Xiaolin. Rapid large frequency offset estimation for DTMB system [J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 225-229.

[6] 刘晓东, 陈卫东. 一种宽范围高精度的载波频偏估计算法 [J]. 无线电工程, 2014, 44(3): 43-45. LIU Xiaodong, CHEN Weidong. Carrier frequency offset estimation algorithm with extended range and high accuracy [J]. Radio Engineering, 2014, 44(3): 43-45.

[7] 聂少军, 何兵哲, 王宏卓. 一种新的大载波频偏估计算法 [J]. 电子设计工程, 2014, 22(1): 168-170. NIE Shaojun, HE Bingzhe, WANG Hongzhuo. A new estimate algorithm of large carrier frequency offset [J]. Electronic Design Engineering, 2014, 22(1): 168-170.

[8] RAHAMIM Y, FREEDMAN A, REICHMAN A. ML iterative tentative-decision-directed (ML-ITDD): a carrier synchronization system for short packet turbo coded communication [C]∥Proceedings of the 2004 11th IEEE Conference on Electronics, Circuits and System. Piscataway, NJ, USA: IEEE, 2004: 346-349.

[9] 史治平, 唐发建, 晏辉. 极低信噪比下的导频联合编码辅助载波同步算法 [J]. 电子与信息学报, 2011, 33(10): 2506-2510. SHI Zhiping, TANG Jianfa, YAN Hui. Joint assisted carrier synchronization algorithm by pilot and code at extremely low SNR [J]. Journal of Electronics & Information Technology, 2011, 33(10): 2506-2510.

[10]FREEDMAN A, RAHAMIM Y, REICHMAN A. Maximum-mean-square soft-output (M2S2O): a method for carrier synchronization of short burst turbo coded signals [J]. IEE Proceedings: Communications, 2006, 153(2): 245-255.

[11]SUN Jinhua, ZHI Jili, WU Xiaojun. A joint pilot and demodulation soft information carrier synchronization for SOQPSK signals [C]∥Proceedings of 2012 5th Global Symposium on Millimeter-Waves. Piscataway, NJ, USA: IEEE, 2012: 512-516.

[12]HERZET C, NOELS N, LOTTICI V, et al. Code-aided turbo synchronization [J]. Proceedings of the IEEE, 2007, 95(6): 1255-1271.

[13]TANG Fajian, SHI Zhiping. Iterative LDPC-Hadamard code-aided carrier frequency synchronization at extremely low SNR [C]∥Proceedings of 2010 Second International Conference on Networks Security Wireless Communications and Trusted Computing. Piscataway, NJ, USA: IEEE, 2010: 314-317.

[14]孙锦华, 王雪梅, 吴小钧. 短突发传输系统的联合导频和迭代译码载波同步 [J]. 西安电子科技大学学报, 2014, 41(1): 29-36. SUN Jinhua, WANG Xuemei, WU Xiaojun. Joint pilot and iterative decoding carrier synchronization for short burst transmission system [J]. Journal of Xidian University, 2014, 41(1): 29-36.

[15]孙锦华, 刘鹏, 吴小钧. 联合旋转平均周期图和解调软信息的载波同步方法 [J]. 电子与信息学报, 2013, 35(9): 2200-2205. SUN Jinhua, LIU Peng, WU Xiaojun. A joint rotational periodogram averaging and demodulation soft information carrier synchronization algorithm [J]. Journal of Electronics & Information Technology, 2013, 35(9): 2200-2205.

[16]MENGLI U, D’ANDREA A N. Synchronization techniques for digital receivers [M]. New York: Plenum Press, 1997: 1-4.

(编辑 刘杨)

Joint Time-Domain and Frequency-Domain Carrier Synchronization Algorithm in Low Signal to Noise Ratio

SUN Jinhua,HAN Huimei

(State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an 710071, China)

A joint time-domain and frequency-domain carrier synchronization (JTDFDCY) algorithm is proposed to improve the low estimation accuracy and small synchronization range of code-aided carrier recovery algorithms in the case of low signal to noise ratio (SNR) for short burst communication systems. The coarse frequency estimations and coarse phase estimations are obtained through processing the pilot symbols by the use of the frequency estimation algorithm, the time estimation algorithm, and the ML algorithm. Then the coarse estimations are used to compensate for the received signal, and the compensated signal are demodulated, decoded, re-encoded and baseband modulated to get the soft decision symbol. The fine frequency estimation and fine phase estimation are obtained through processing the soft decision symbol by using summation of time-domain correlation and ML algorithm, and eventually, more efficient synchronization carrier is realized. Simulation results show that the proposed JTDFDCY algorithm can satisfy the requirements of frequency estimation range and root mean square error. When the normalized frequency offset is in the range of (-0.5,0.5), the performance degradation of the JTDFDCY algorithm is within 0.1 dB at the cost of 6.1% pilot combining with decoder information.

low signal to noise ratio; pilot; carrier synchronization; code-aided

2014-04-14。

孙锦华(1979—),女,博士,副教授。

国家自然科学基金资助项目(61271175);中央高校基本科研业务费专项资金资助项目(JB140114,K5051201043)。

时间:2014-11-28

10.7652/xjtuxb201502011

TN911.3

A

0253-987X(2015)02-0062-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141128.1611.002.html