采用频域融合方法的砂轮刀具磨损三维重构技术

朱爱斌,胡浩强,何大勇,陈渭

(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)



采用频域融合方法的砂轮刀具磨损三维重构技术

朱爱斌,胡浩强,何大勇,陈渭

(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)

针对聚焦合成方法在砂轮刀具磨损区域三维重构过程中高度值离散的问题,运用傅里叶变换将聚焦合成方法与明暗形状恢复方法相结合,提出了聚焦合成方法的高度值连续化新方法。运用傅里叶变换,在频域中对聚焦合成方法形成的三维重构图像进行高通滤波,对明暗形状恢复方法形成的三维重构图像进行低通滤波,并将滤波后的图像在频域叠加,经过傅里叶反变换,得到空间域融合后的刀具磨损区域三维重构图像。分析和实验表明,融合后的三维重构图像同时保留了聚焦合成方法中蕴含的离散几何高度信息和明暗形状恢复方法中蕴含的表面细节特征信息,能有效避免由于聚焦合成方法中高度值离散带来的误差。

刀具磨损;聚焦合成;明暗形状恢复;傅里叶变换

刀具的磨损一直是机械加工中的重点和热点研究问题[1]。刀具磨损区域形貌的三维重构对刀具磨损区域的观察和测量以及对磨损机理的研究具有重要的意义。聚焦合成(depth from focus,DFF)方法根据显微成像过程中焦距、像距、物距之间的关系,能够建立显微图像序列之间的高度关系。姜志国等运用改进的拉普拉斯聚焦算子和区域小波变换的方法,实现了序列图像的融合显示和三维重构[2],但需依赖插值的方法解决重构过程中的高度值离散问题,而且对序列图像高度之间进行插值时需要依靠序列图像的数量来保证所用方法的精度。童晨等在解决DFF方法中的高度值离散问题时,也是运用了高斯插值的方法[3]。目前,解决DFF方法的高度值离散问题通常采用的是插值或者对像素领域取平均值的方法[4]。这2种方法缺少直接的物理与几何依据,虽然能起到离散值连续化的作用,但是盲目性与随意性比较大。

20世纪70年代,Horn等人提出了明暗形状恢复(shape from shading, SFS)方法,其原理是利用物体表面明暗度的变化,解析出表面的法向矢量信息,从而转换为物体表面的高度信息[5]。须明和赵荣椿等对SFS方法进行了调研,指出了现有SFS求解方法的病态性,对SFS方法的各种解法以及恢复出的表面形状的特点进行了综述[6]。Tsai等指出,SFS方法得到的表面高度图像一般是连续的,包含较多的细节信息,并提出将立体视觉与SFS方法相结合,通过对立体视觉以及SFS恢复方法得到的图像进行频域内的滤波与融合之后,得到质量更好的立体图像[7]。虽然融合后的图像在形状上较原来的2种方法均有所改善,但是这种方法缺少直接有力的证据说明采用滤波的依据以及物理几何意义。

综上所述,DFF方法采用的各种聚焦评价函数对序列图片中聚焦清晰位置像素点的检测能力不同,而采用何种聚焦评价函数并没有严格的依据,并且,DFF方法中离散高度值连续化过程中采用的连续化算法也只是对实际表面的一种近似插值,故DFF方法的精度误差来源主要为聚焦评价函数的选择和离散过程中离散高度值连续化方法的选择2个方面。SFS方法由于本身的不确定性、在模型求解过程中添加的假设和约束条件以及模型求解采用的方法的复杂度不同,都给SFS方法的表面重构结果带来了误差。

本文通过傅里叶变换将基于拉普拉斯算子的DFF方法与基于朗伯表面几何光照模型的SFS方法相结合,对DFF方法中存在的图像之间缺失的高度信息,通过SFS方法进行补充,以期为解决DFF方法中高度值的离散问题提供一种新思路。

1 DFF方法的基本原理

对于一个理想的光学系统,在近轴光学理论中其像距v、物距u、焦距f满足以下关系式

(1)

显微镜的景深是有限的,对于显微镜系统,像距v一般是固定的,与之对应的物距u也是确定的,因此当物体在显微镜载物台上移动时,如图1所示,物体由移动前位置1移动到移动后位置2,只有物体表面上距物镜u附近的部分(即景深内的部分)才能在图像采集设备感应平面上成清晰的像,其余部分则在感应平面上成模糊的像。随着物距u的改变,焦距f和像距v不发生变化,根据透镜成像公式,由显微镜和图像采集设备获得的图像只有在景深范围内是聚焦的,聚焦平面位置不变,而物体上能够清晰成像的位置发生了改变,那么投射到像平面上能够清晰成像的区域也会发生改变[8]。

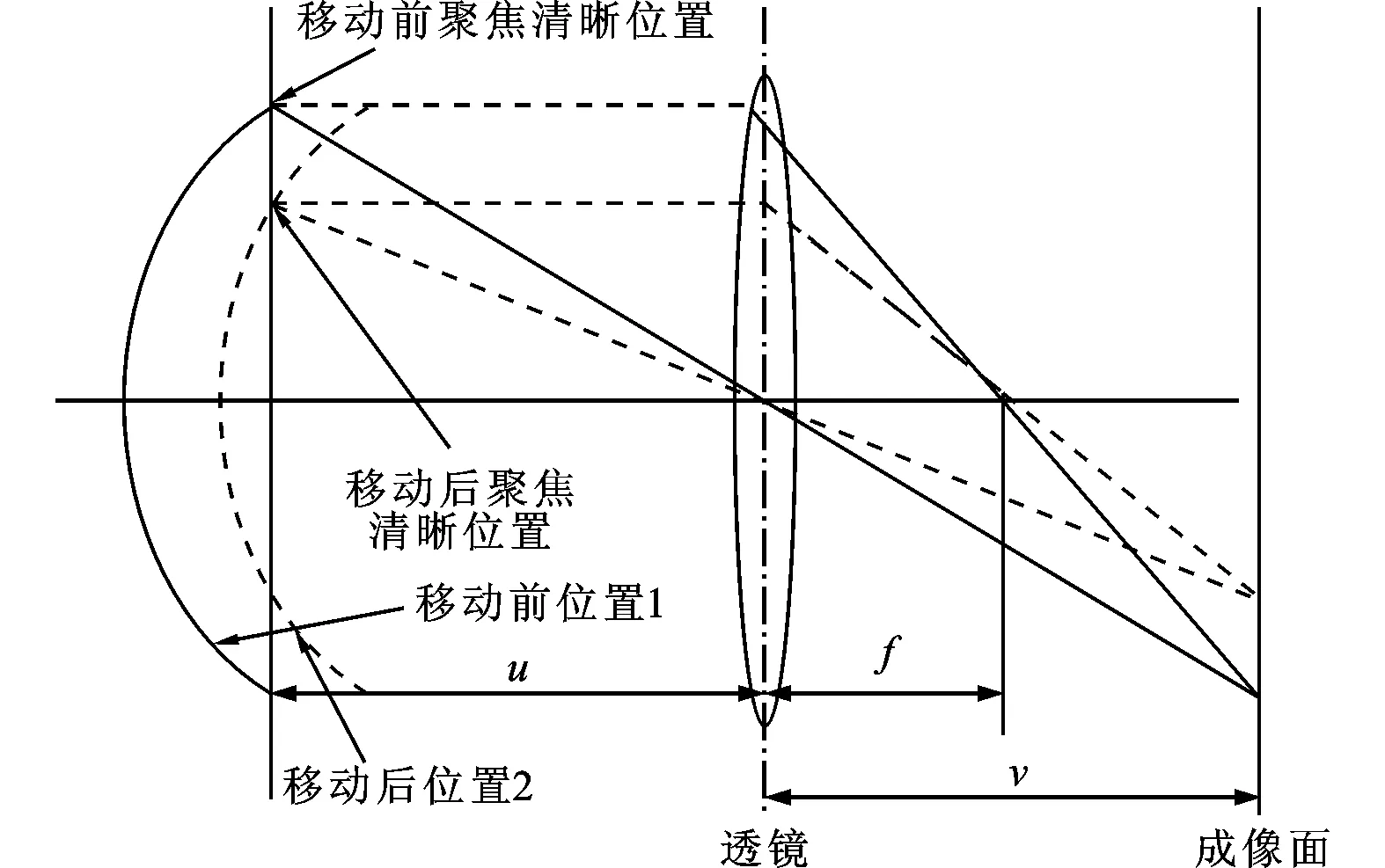
图1 透镜成像原理图

DFF方法是通过获取不同物距下的显微样本序列图像,使整个序列中每幅图像有聚焦清晰区域和模糊区域,然后在序列图像中通过一定的融合规则获取每一个像素对应的聚焦清晰位置,据此获得高度索引图像,再通过一定算法恢复深度信息。DFF的原理如图2所示,恢复过程一般是对高度索引图像之间的高度信息进行补充,恢复出比较精确的物体深度信息。由图2可知,DFF方法只能得到离散序列的高度值,而且恢复出的高度图精度取决于离散序列的数量。

图2 聚焦合成原理示意图

2 采用改进拉普拉斯算子的DFF方法

DFF方法获取每一个像素对应的聚焦清晰位置时,通常通过聚焦评价函数对图像中的像素点及其领域像素点的灰度进行某种比较。常见聚焦评价函数采用的算子为灰度梯度算子,包括Roberts梯度算子、Sobel梯度算子、拉普拉斯梯度算子等。傅里叶变换和小波变换为DFF方法提供了新的思路,但是这种变换的几何以及空间意义并不明显,在某些场合对像素点的检测能力与常见的空间域评价算子相比并无太大优势[9]。一个好的聚焦评价函数应对图像灰度的方向变化不敏感,具有较强的抗噪声能力,而且一般聚焦评价函数最大值的位置即为聚焦位置[10-11]。

本文采用改进的拉普拉斯梯度算子(ML)作为聚焦评价函数。拉普拉斯梯度算子是一种二阶微分算子,考虑到聚焦评价函数对于方向的不敏感性,所以取x和y方向的导数的绝对值。虽然作为二阶微分改进的拉普拉斯梯度算子对于噪声可能比较敏感,但是考虑到显微图像中纹理的变化以及后续对图像在频率域的滤波处理,选用改进的拉普拉斯梯度算子是比较合理的

∑|2f(x,y)|=

(2)

式中:f(x,y)代表图像中横坐标为x、纵坐标为y的像素点的灰度值。由于数字图像可以看成一个实数矩阵,所以一般用差分代替上式所述微分。

ML(x,y)=

|2f(x,y)-f(x-s,y)-f(x+s,y)|+

|2f(x,y)-f(x,y-s)-f(x,y+s)|

(3)

(4)

式中:f(x,y)为点(i,j)处的灰度值,表示该点的聚焦测度;ML(x,y)为图像在(x,y)点处的拉普拉斯梯度算子;s为可变步长,一般取3;Lfocus所对应的位置就是聚焦位置。

3 基于朗伯几何光照模型的SFS恢复算法

在理想漫反射情况下,物体表面的灰度满足如下反射图方程

E(x,y)=R(p,q)=

(5)

式中:E(x,y)为图像在像素点(x,y)的照度;R(p,q)对应物体表面法向量方向(p,q)的反射图;(p0,q0)为光源入射方向。根据Tsai等提出的一种求解上述反射图方程的算法[7],通过将p和q用差分的方法表示为

(6)

(7)

并且将上述反射图方程在固定点处进行一阶泰勒展开,可以得到每一像素点处的反射图方程。一幅图像有N×N像素就需要求解N2个等式,所以通过雅可比迭代方法,经过化简可以得到以下迭代求解方程来代替原来的线性方程组求解过程

Zn(x,y)=Zn-1(x,y)+

(8)

式中

(9)

设Z0(x,y)=0,初始迭代条件由本文实验条件选择为表面法向量初值p0=0,q0=0,光源为垂直入射,则光源向量p0=0,q0=0。

4 DFF与SFS方法的结合

由于DFF方法得到的重构图像精度取决于载物台上物距变化的精度,如果获取的序列图像数量过少的话,对于高度序列图像之间的高度值就需要进行插值。较常见的插值技术为高斯插值法。这里将SFS方法与DFF方法相结合。SFS方法得到的重构图像一般是连续的,但是由于SFS恢复方法缺少强有力的外界物理或几何约束条件,所以方程一般是病态的,需要增加假设条件和简化才能使得该方法有收敛的解。即使如此,该方法的稳定性和可靠性依然较差,运用SFS方法一般只能得到方程的近似解,恢复出的表面形状也只是形状上与真实表面相似而已。然而,SFS方法所采用的模型依赖的是光度学原理与物体表面的形状特征,所以SFS方法提供的近似解包含着重构区域的细节信息,理论上可以补充DFF方法所丢失的高度信息和表面形状特征的细节信息。

首先通过下式对SFS恢复方法得到的三维重构图进行标定

(10)

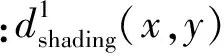
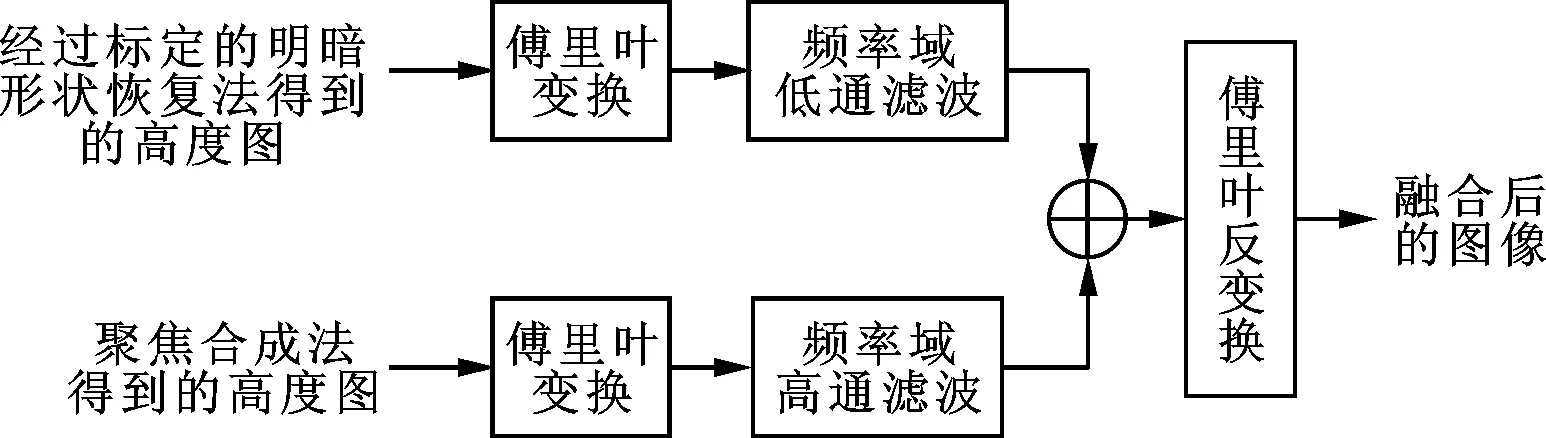
图3 频域融合算法示意图

滤波选择高斯滤波器。高斯低通滤波器的频域表达式为

(11)

相应的高斯高通滤波器的频域表达式为

(12)

5 实 验

实验中采用奥林巴斯DSX500光学数码显微镜,放大倍数调节为69倍,刀具对象为绿碳化硅砂轮。DSX500本身带有DFF功能,但是一般需要20张以上的图片数量。本文所用图像的实际大小为3.989 mm×3.989 mm,调节步长为0.165 mm,而实验得到的三维重构图片在水平面上的大小为1 200×1 200像素。

使用20张序列图片中的4张(如图4所示),这4张图片中必须包括聚焦过程中处于极限位置的2张图片。由基于拉普拉斯梯度算子的DFF方法融合后的图像如图5所示。将图4所示图片转化为灰度图像之后,利用DFF方法进行磨损区域三维表面重构,结果如图6所示。对图5利用SFS方法进行磨损区域三维表面重构,结果如图7所示。

图4 实验选用的4张刀具磨损图片

图5 由基于拉普拉斯梯度算子的DFF方法融合后的图像

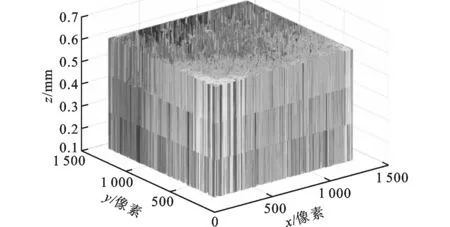
图6 DFF方法得到的刀具磨损区域高度图

由图6可以看出,采用DFF方法直接对包含有背景的序列图片进行三维重构不能有效地去除噪声影响,且高度值为离散值,很难直接辨别出磨损区域的形状。图7为采用SFS方法的重构图像,可见由图7基本不能得出磨损区域的三维形状。

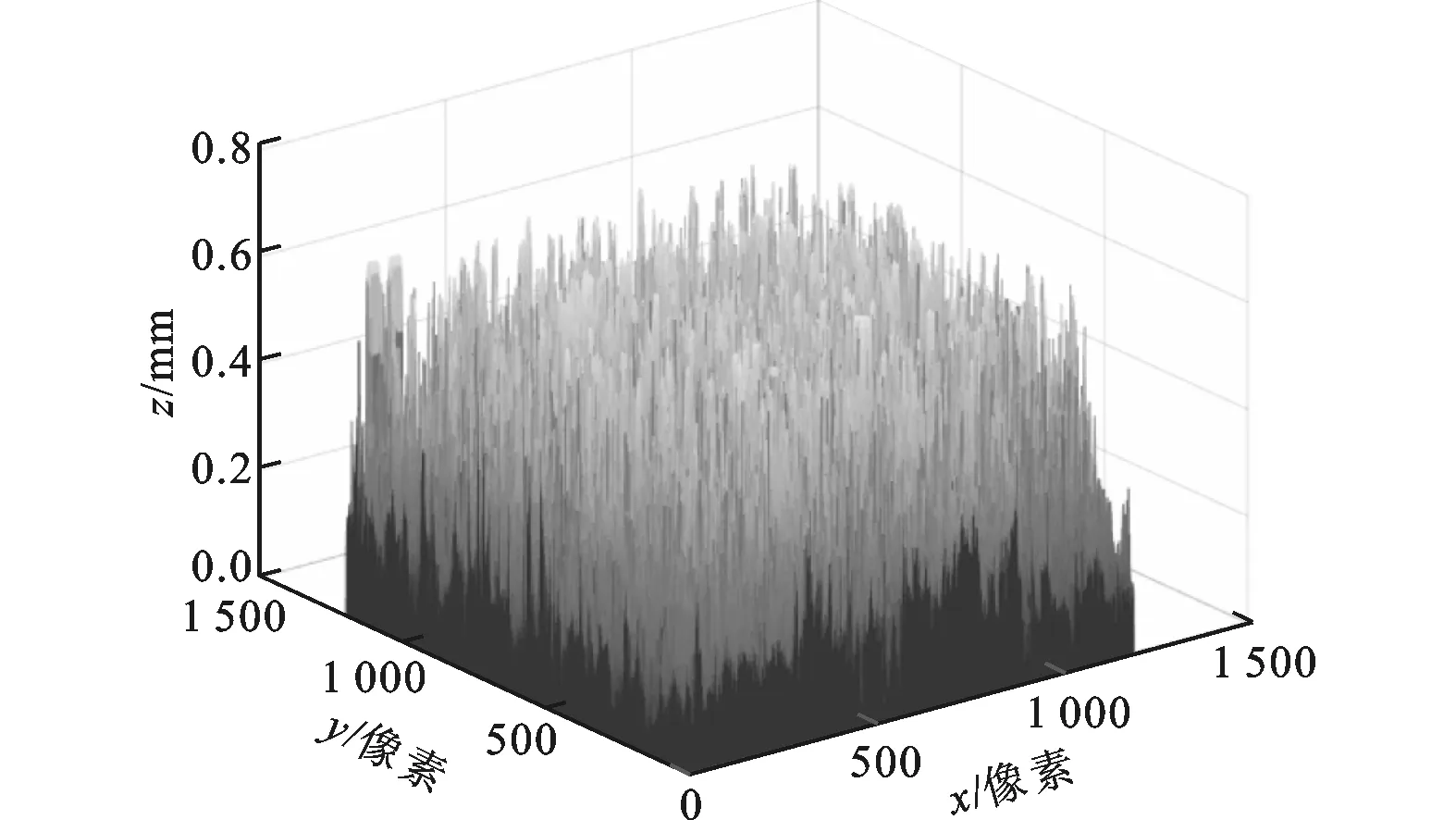
图7 SFS方法得到的刀具磨损区域高度图

图8为采用本文所用融合方法得到的三维表面重构图像,可以看出经过滤波与频域融合之后图像的连续性大大提高,并且能够有效滤除噪声对重构图片的影响,磨损区域的形状特征也比较明显,与图9所示DSX500显微镜使用20张序列图片重构得到的图像相比具有相同的高度趋势,均为朝一个方向倾斜的斜坡。

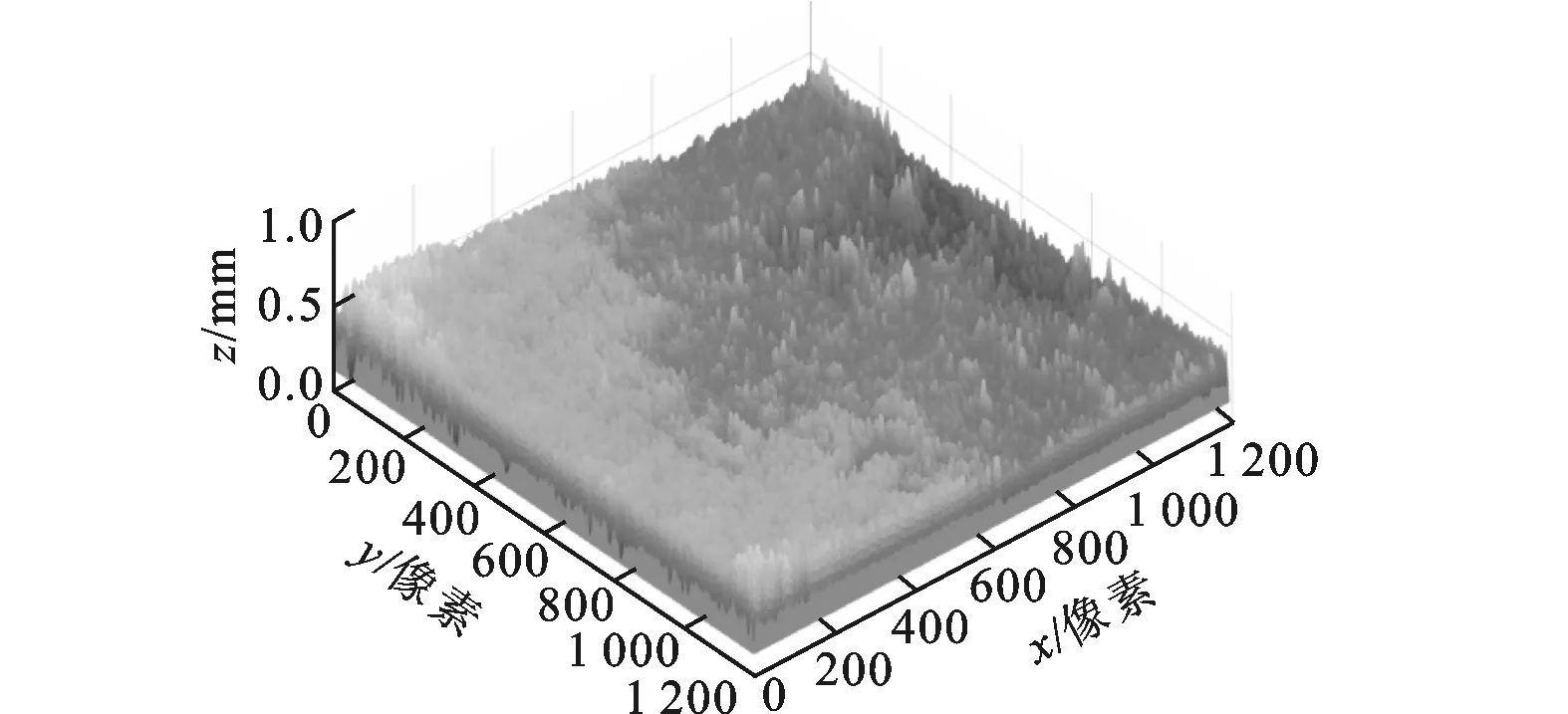
图8 本文频域融合方法得到的刀具磨损区域高度图

图9 利用DSX500显微镜得到的刀具磨损区域高度图

如表1所示,由DSX500显微镜获得的标准三维重构图可得到磨损体积为1.738 mm3,运用DFF方法计算的磨损体积为2.068 mm3,运用SFS方法计算的磨损体积为2.725 mm3,经频域融合后计算的磨损体积为1.942 mm3。经频域融合后计算的磨损体积与显微镜使用20张图片得出的结果相差11.74%,相对单独使用DFF和SFS方法在精度方面有明显提升。

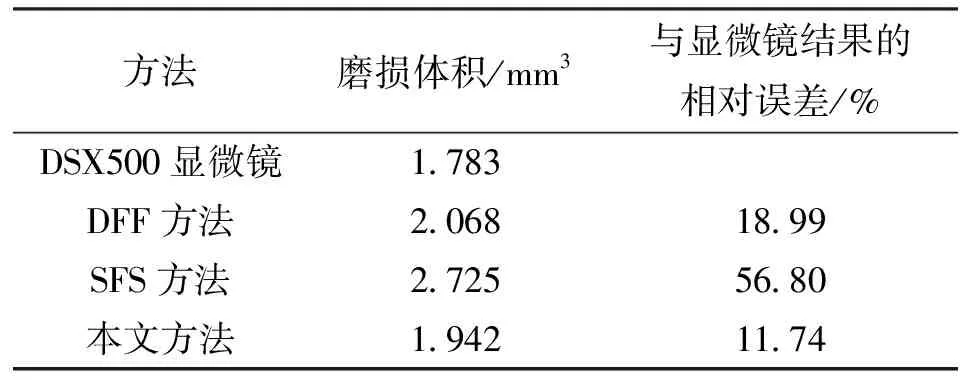
表1 3种方法计算得到的磨损体积相对误差比较

6 结 论

本文通过傅里叶变换将基于拉普拉斯梯度算子的DFF方法与基于朗伯表面几何光照模型的SFS方法相结合,对DFF方法中存在的图像之间缺失的高度信息,通过SFS方法进行补充。对于DFF方法,其精度主要取决于采集图像序列之间的距离,序列图像离散高度值的连续化是DFF方法精度误差的主要来源之一。本文运用傅里叶变换,在频域中对DFF方法形成的三维重构图像进行高通滤波,对SFS方法形成的三维重构图像进行低通滤波,并将滤波后的图像在频域进行叠加,经过傅里叶反变换,得到空间域融合后的刀具磨损区域三维重构图像。

分析和实验结果表明,在频域中对DFF和SFS重建方法进行融合相对于单独采用这2种表面重构方法,融合后的三维重构图像同时保留了DFF方法中的离散几何高度信息和SFS方法中的表面细节特征信息,能有效避免由于DFF方法中高度值离散带来的误差,从而提升砂轮表面磨损区域的重构精度。

研究频域融合算法在其他磨损表面的适用性,将是我们下一步工作的重点。

[1] 董卫平, 蔡礼君, 卢秉恒. 刀具磨损监测的双向切削力相干函数法 [J]. 西安交通大学学报, 1988, 22(5): 101-106. DONG Weiping, CAI Lijun, LU Bingheng. Bidirectional cutting force and tool wear monitoring coherence function method [J]. Journal of Xi’an Jiaotong University, 1988, 22(5): 101-106.

[2] 姜志国, 韩冬兵, 谢凤英. 基于全自动显微镜的图像新技术研究 [J]. 中国体视学与图像分析, 2004, 9(1): 31-36. JIANG Zhiguo, HAN Dongbing, XIE Fengying. New image techniques based on automatic microscopy [J]. Chinese Journal of Stereology and Image Analysis,2004, 9(1): 31-36.

[3] 童晨, 何宁, 李亮. 刀具磨损三维形貌的测量及评价方法 [J]. 机械制造与自动化, 2008, 37(5): 57-60. TONG Chen, HE Ning, LI Liang. Methods to measure and evaluate 3D topography of tool wear [J]. Mechanical Manufacturing and Automation, 2008, 37(5): 57-60.

[4] PAN W. Multiplane imaging and depth-of-focus extending in digital holography by a single-shot digital hologram [J]. Optics Communications, 2013, 286: 117-122.

[5] HORN B K P. Shape from shading: a method for obtaining the shape of a smooth opaque object from one view [D]. Cambridge, MA, USA: MIT, 1970.

[6] 须明, 赵荣椿. SFS方法及其与立体视觉方法的集成方案综述 [J]. 计算机工程与应用, 2006, 42(8): 1-6. XU Ming, ZHAO Rongchun. Review: on integration of stereo and shape from shading [J]. Computer Engineering and Applications, 2006, 42(8): 1-6.

[7] TSAI P S, SHAH M. Shape from shading using linear approximation [J]. Image and Vision Computing Journal, 1994, 12(8): 487-488

[8] 刘莉, 姜志国, 谢凤英. 光学体视显微图像立体测量系统研究与开发 [J]. 中国体视学与图像分析, 2003, 8(4): 220-224. LIU Li, JIANG Zhiguo, XIE Fengying. New image techniques based on automatic microscopy [J]. Chinese Journal of Stereology and Image Analysis, 2003, 8(4): 220-224.

[9] 熊四昌, 杨涌, 胡东. 基于小波分析的显微序列图像合成系统 [J]. 光学仪器, 2006, 28(6): 28-32. XIONG, Sichang, YANG Yong, HU Dong. The microscopy serial image synthesis based on the wavelet analysis [J]. Optical Instrument, 2006, 28(6): 28-32.

[10]童晨. 刀具磨损区域的三维重构技术研究 [D]. 南京: 南京航空航天大学, 2008.

[11]MALIK A S, CHOI T. A novel algorithm for estimation of depth map using image focus for 3D shape recovery in the presence of noise [J]. Pattern Recognition, 2008, 41(7): 2200-2225.

(编辑 葛赵青)

Three-Dimensional Reconstruction of Tool Wear Area for Grinding Wheel Using Frequency-Domain Fusion Method

ZHU Aibin, HU Haoqiang, HE Dayong, CHEN Wei

(Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China)

Aiming at the problem of the discontinuous height values in the three-dimensional reconstruction of tool wear area for grinding wheel using the method of depth from focus (DFF), a new method for continuing the height values with DFF is proposed by using Fourier transform to combine the methods of DFF and shape from shading (SFS). Using Fourier transform in the frequency domain, performing highpass filtering for the 3D reconstruction image of DFF and lowpass filtering for the 3D reconstruction image of SFS, and superimposing the filtered image in the frequency domain, the 3D reconstruction image of the tool wear area of grinding wheel can be obtained by inverse Fourier transform to fuse in the spatial domain. Analysis and experimental results show that the fused 3D reconstruction image not only retains the discrete geometric height information contained in DFF and the detailed surface information contained in SFS, but also effectively avoids the errors caused by the discontinuous height values in the DFF.

tool wear; depth from focus; shape from shading; Fourier transform

2014-09-06。

朱爱斌(1975—),男,博士,副教授。

国家自然科学基金资助项目(51175409)。

时间:2015-03-02

10.7652/xjtuxb201505013

TH113.2

A

0253-987X(2015)05-0082-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150302.1653.003.html