车致脉动力作用下桥上防风屏障的振动响应分析

张田，郭薇薇，杜宪亭

(1．大连海事大学道路与桥梁工程研究所，辽宁大连116026;2．北京交通大学土木建筑工程学院，北京100044)

车致脉动力作用下桥上防风屏障的振动响应分析

张田1，郭薇薇2，杜宪亭2

(1．大连海事大学道路与桥梁工程研究所，辽宁大连116026;2．北京交通大学土木建筑工程学院，北京100044)

高速铁路桥上的防风屏障会受到列车运行产生的脉动气冲力作用，防风屏障在脉动气冲力作用下的振动是防风屏障设计必须考虑的问题。本文建立了防风屏障有限元模型，考虑自然风荷载、结构自重和列车引起的脉动风荷载，以兰新铁路第二双线桥上防风屏障为实例，分析防风屏障各关键节点处的振动响应。结果表明:考虑自然风及车致气动力的脉动特性会显著增加防风屏障的动力响应;分析车致气动力对防风屏障的结构响应时应将自然风基本风压作为静载同时计算;另外应特别关注挡风板的振动，其响应远高于立柱。

桥梁 高速铁路 自然风场 车致脉动力 防风屏障 振动响应

为了保证高速铁路桥上列车的运行安全，安装防风屏障是一项有效的措施［1-2］。然而，关于防风屏障在自然风及车致脉冲力作用下的振动响应计算分析较少，大多分析以声屏障为研究对象［3-7］。本文基于有限元法建立防风屏障模型，考虑自然风荷载、结构自重和列车引起的脉动风荷载。根据有关研究［3］，可把真实长度的声屏障大模型简化为小规模具有代表性的有限段声屏障来进行计算。类似于声屏障，由于风屏障在长度方向上均由相同的结构单元组成，也可以同样处理。本文以箱梁桥上安装单侧4 m防风屏障为例建立有限元模型，分析各种工况下防风屏障关键点处的振动响应。

1 自然风脉动风压时程

风屏障结构动力分析时多采用脉动风压计算，因此应将脉动风速谱转化为脉动风压谱。一般将风速看成平均风速和脉动风速vf的叠加，类似地将风压也看作平均风压与脉动风压wf的叠加，即

基本风速和基本风压的关系为

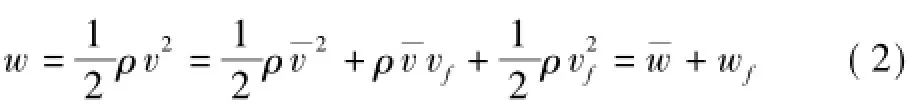
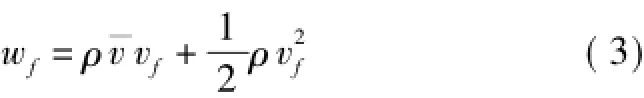
因此，脉动风压wf的方差为

由于脉动风速vf与平均风速相比为小量，可忽略上式变为

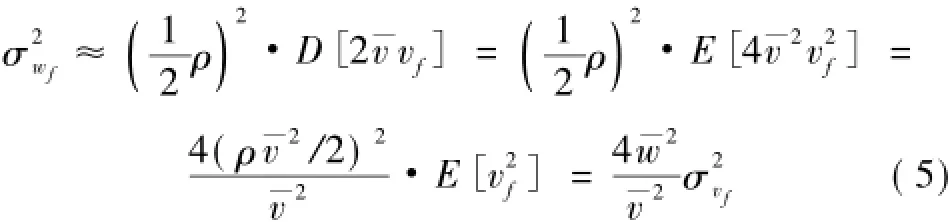
因此脉动风压功率谱密度Sw(n)和脉动风速功率谱密度Sv(n)之间的关系为

根据《公路桥梁抗风设计规范》［8］，水平脉动风速功率谱的具体形式为

式中:v1为标准高度z1(一般为10 m)处的平均风速，m/s;z0为地面粗糙高度，m。

对应的脉动风压功率谱Sw(n)为

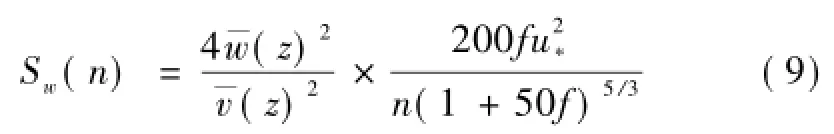
因此，可由谐波叠加法根据脉动风压功率谱模拟脉动风压时程，可写为

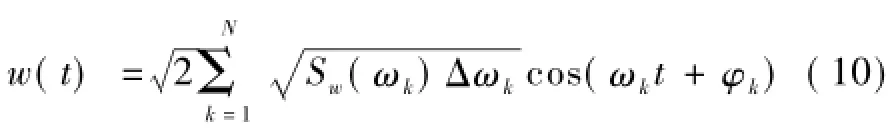
式中:w(t)为脉动风压时程;ωk(k=1，2，…，N)为所考虑频率，其中ω1，ωN分别为频率的上下限;Δωk为频率间隔;φk为均匀分布于［0，2π］上的随机相位角。

于是风屏障结构上脉动风压时程函数可写为

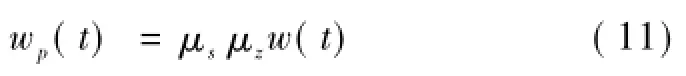
式中:μs为风荷载体型系数，μz为风压高度变化系数，均可以按《建筑结构荷载规范》(GB 50009—2001)［9］取值。

2 风屏障上车致脉动力时程计算方法

德国铁路公司基于高速列车旁声屏障的测量结果提出了列车脉动风荷载公式

式中:wt(t)为列车脉动风荷载;cz为轨面以上的高度系数，试验的轨道以上声屏障高度为3 m，则cz在声屏障的上端为0.6，并线性变化至上部2/3高度处的1.0，下部1/3高度处为1.0;ρ为空气密度;vt为列车速度;cp为脉动风压力系数，取决于列车类型和声屏障与轨道中心线的距离，表达式为

式中:D为声屏障至轨道中心距离;cp(3.8)为声屏障与轨道中心线相距3.8 m时的无量纲脉动风压力系数，该值取决于时间并基于实测结果确定。

德国研究资料［10］对ICE3列车运行速度为300 km/h时的cp(3.8)建议值如图1所示。

图1 德国ICE3列车的cp(3.8)曲线

对于其它速度，时间坐标按如下方式转换

作用于声屏障的气动脉动力荷载与风屏障相似，也可以采用上述公式来计算。

3 实例分析

以兰新铁路第二双线上简支箱梁安装单侧4 m防风屏障为例，在有限元软件ANSYS中建立计算模型。立柱采用Beam 188单元、挡风板采用Shell 63单元。计算条件为ICE3列车以速度300 km/h运行，引起的脉动力作用于风屏障，轨道中心线与屏障间距为3.8 m。每两根立柱间的挡风板细部模型如图2所示。

图2 每两根立柱间的挡风板细部模型

由前述方法可获得风屏障上的自然风脉动风压时程曲线以及列车运动引起的风屏障脉动风荷载时程曲线，如图3和图4。按一致输入的方式计算防风屏障的瞬态动力响应，此处主要计算分析防风屏障的横向响应。

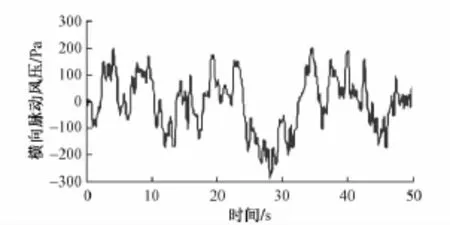
图3 风屏障上的自然风脉动风压时程曲线

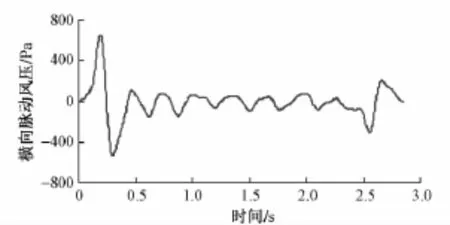
图4 风屏障上的车致脉动风压时程曲线

为了分析脉动力作用与静力作用下风屏障振动响应的差异，计算时考虑静力分析和动力分析两种情况。

静力计算设置如下两种工况。

工况①:将自然风基本风压作为静载(基本风压取为800 Pa);

工况②:将防风屏障上气动力时程荷载的峰值压力作为静载(取为657 Pa)。

因为自然风荷载为长周期作用，而列车气动脉冲力作用时间很短，因此在设置计算工况时，不考虑列车气动脉冲力与自然风脉动风压的组合，即动力计算设置如下5种工况。

工况③:车致气动脉冲力时程荷载;

工况④:自然风脉动风压时程荷载;

工况⑤:结构自重+自然风脉动风压时程荷载;

工况⑥:结构自重+自然风脉动风压时程荷载(含基本风压);

工况⑦:结构自重+自然风基本风压(作为静载) +车致气动脉冲力时程荷载。

以中间一段2 m的风屏障为例，列出风屏障关键点处横向位移计算结果，见表1，主要包括如下节点:左立柱顶部节点(A点)，挡风板顶部中间节点(B点)，左立柱中间节点(C点)，右立柱顶部节点(D点)，右立柱中间节点(E点)，挡风板中部中间节点(F点)，挡风板底部中间节点(G点)。为了分析列车引起的气动脉冲荷载的动力效应，定义动力放大系数η为η=R/R0。其中，R为风屏障某一节点脉动风致响应最大值，R0为某一节点在气动脉冲荷载峰值静力计算时的响应值。

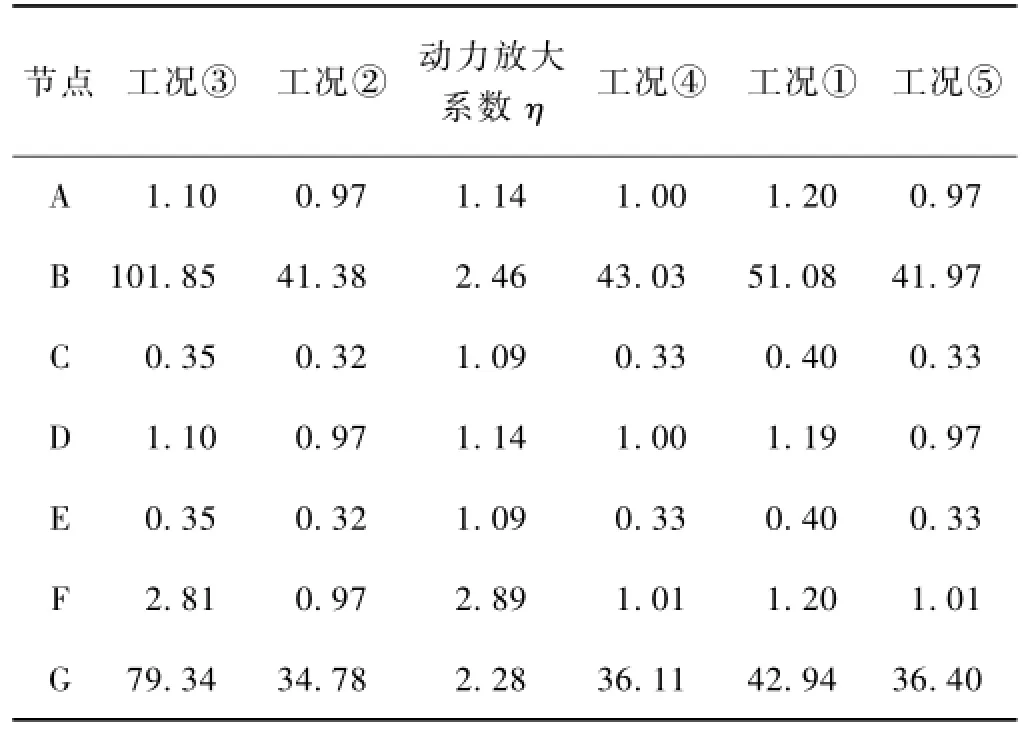
表1 风致屏障位移响应时程分析与静力分析比较

从表1可以看出，防风屏障关键点处的位移动力计算时的结果高于静力计算时，特别是挡风板顶部中间和挡风板中部中间，动力放大效应更加明显，因此计算列车运行导致的风屏障响应时需要采用时程分析方法，仅仅采用静力计算会低估风屏障结构的响应。另外，从图3可知，模拟的自然风脉动风压最大值为285 Pa，而自然风基本风压为800 Pa，则自然风脉动风压最大值与自然风基本风压的比值约为0.356;但是从响应计算结果可以看出，表1所列出的关键点处由自然风脉动风压引起的位移响应最大值与自然风基本风压作为静载计算时位移响应的比值却达到0.84。可见，考虑自然风的脉动特性会大大增加结构的位移响应。

比较表1中工况④与工况⑤的位移，可以发现是否考虑结构自重对风屏障横向位移影响很小，二者的差别在3%以下;有自然风脉动风压时程荷载(含基本风压)，即工况⑥，与仅有自然风脉动风压时程(不含基本风压)，即工况⑤，两种工况下屏障的位移响应时程曲线形式基本相同。图5为挡风板顶部中间节点的横向位移响应。图6为左立柱顶部横向位移时程曲线。显然包含基本风压的计算结果大于不包含基本风压的计算结果，而且响应曲线的形式与时程荷载的作用形式非常相似。

图5 挡风板顶部中间节点的横向位移时程曲线

图6 左立柱顶部节点的横向位移时程曲线

对工况⑦，即计算列车运行引起的气动脉冲力对风屏障的作用，考虑了自然风基本风压，将其作为静载施加于结构上，与工况③相比，防风屏障各关键点的响应均大幅增加。同时，可以发现各工况时挡风板的位移响应大于立柱的位移响应。

工况⑦时的风屏障立柱不同节点的位移响应时程曲线如图7所示，挡风板不同节点的位移时程曲线如图8所示。

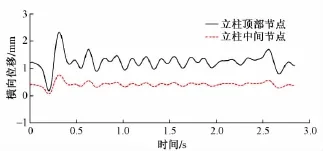
图7 工况⑦时立柱的横向位移时程曲线

图8 工况⑦时挡风板的横向位移时程曲线

从图7、图8可以看出:考虑自然风基本风压作为静载时，立柱顶部和中间节点的横向位移差别更大，并且立柱节点位移的最大值约为不考虑基本风压时的2倍;挡风板的横向位移也大幅增加，约为不考虑基本风压时的1.5倍;挡风板顶部和底部的响应较大，应采取适当措施予以加强。

实际工程计算时，需要按工况⑥计算自然风荷载对风屏障的作用，而对车致风屏障上的气动脉冲力，同时需要考虑外部自然风场时，可以按照工况⑦进行分析。

4 结论

基于对高速铁路桥上防风屏障自然风脉动风压时程和车致脉动力时程的计算，并进行防风屏障的瞬态分析，得出如下结论:

1)计算列车气动脉冲力引起的防风屏障振动时，防风屏障关键点处的位移在动力计算时的结果高于静力计算时，特别是挡风板顶部中间节点和挡风板中部中间节点，动力放大效应更加明显，动力放大系数达到约2.5。

2)计算自然风引起的防风屏障响应时，将自然风按基本风压作为静载计算会低估结构的位移响应，考虑自然风的脉动特性会大大增加结构的位移响应。

3)各种工况下，挡风板的横向位移远大于立柱，立柱的顶部大于中间，挡风板的底部和顶部中间横向位移均较大，中部中间较小，而且位移响应在列车驶入和驶出时较大。

4)计算列车运行引起的气动脉冲荷载对风屏障的作用时，需要考虑自然风的作用，可将其基本风压作为静载，即按结构自重、自然风基本风压作为静载与列车引起的气动脉冲力时程荷载组合进行时程分析计算。

［1］Tatsuo Noguchi，Toshishige Fujii．Minimizing the Effect of Natural Disasters［J］．Japan Railway＆Transport Review，2000(23):52-59．

［2］Toshishige Fujii，Tatsuo Maeda．Wind-induced Accidents of Train/Vehicles and Their Measures in Japan［J］．QR OF RTRI，1999，40(1):50-55．

［3］赵丽滨，龙丽平，蔡庆云．列车风致脉动力下声屏障的动力学性能［J］．北京航空航天大学学报，2009，35(4):505-508．

［4］焦长洲，高波，王广地．声屏障结构的列车脉动风致振动分析［J］．西南交通大学学报，2007，42(5):531-536．

［5］戚振宕，李人宪．高速铁路声屏障气动特性仿真分析［J］．路基工程，2011，157(4):9-12．

［6］吕坚品．高速铁路插板式及整体式声屏障结构研究［D］．南京:东南大学，2010．

［7］李红梅，宣言，王澜，等．高速铁路声屏障脉动力数值模拟研究［J］．铁道建筑，2013(1):27-30．

［8］中交公路规划设计院．JTG/T D60-01—2004公路桥梁抗风设计规范［S］．北京:人民交通出版社，2004．

［9］中华人民共和国建设部．GB 50009—2001建筑结构荷载规范［S］．北京:中国建筑工业出版社，2006．

［10］邓跞，施洲，刘兆丰．高速铁路声屏障动力特性研究［J］．铁道建筑，2009(11):101-104．

Analysis of vibration response of bridge's wind barrier to fluctuating force induced by train running

ZHANG Tian1，GUO Weiwei2，DU Xianting2
(1．Institute of Road and Bridge Engineering，Dalian Maritime University，Dalian Liaoning 116026，China; 2．School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China)

T he wind barrier on the high-speed railway bridge is subject to the fluctuating force induced by the running train．T he vibration response of the barrier under the fluctuating force shall be taken into account in the wind barrier design．A finite element model of wind barrier was established to calculate the vibration response considering the load combination of the natural wind load，the self-weight of the structure and the fluctuating load．T he wind barrier on the bridge in new built Lanzhou-Xinjiang railway line was taken as an example．T he vibration responses of the key nodes in the model were calculated．T he results revealed that the dynamic response of the wind barrier greatly increased when considering the fluctuating characteristic of the natural wind and aerodynamic force induced by the train．T he vibration response calculation of the wind barrier shall be calculated considering the combination of the aerodynamic force induced by the train and the basic wind pressure of the natural wind as the static load．Additionally，the vibration of the windbreak plate of the barrier shall be carefully designed，whose response was much higher than that of stand column．

Bridge;High speed railway;Natural wind field;T rain-induced fluctuating force;W ind barrier;Vibration response

TU311．3

A

10．3969/j．issn．1003-1995．2015．03．02

1003-1995(2015)03-0005-05

(责任审编李付军)

2014-06-09;

2014-07-20

国家重点基础研究发展计划项目(973项目) (2013CB036203);中央高校基本科研业务费专项资金资助项目(3132014071);国家自然科学基金项目(51308034)

张田(1986—)，男，湖北荆州人，讲师，博士。