基于逆波兰算法实现的电力录波数据分析公式编辑器

曾水根 丁俊健 刘万斌

摘要：本文首先对继电保护技术在日益壮大与复杂的电网安全运行中重要性进行分析，指出了电力录波波形重现技术在电网安全运行中的重要性，继而基于逆波兰算法实现了一种电力录波数据分析公式编辑器。随后基于公式编辑器的设计思路进行分步解析予以实现，同时将该公式编辑器应用于实践。

关键词：电网；继电保护；录波数据；数据分析；逆波兰；公式编辑器

中图分类号：TP399

文献标识码：B

DOI： 10.3969/j.issn.1003-6970.2015.08.026

0 引言

随着电力需求的快速增长，电力网络规模也日益壮大，电网结构越来越复杂，电网安全显得日益重要。基于此，作为电网安全运行重要保障的继电保护技术在近些年获得了突飞猛进的发展。电力录波技术能够正确评价继电保护装置的工作情况，在保护装置动作时有利于帮助我们准确地找出电网运行的录波点，以及时采取有效措施，减少电网录波发生概率，尽量降低损失。但电力录波技术的录波数据并不是直观的事故分析数据，所以我们需要将计算机软件技术应用于电力录波数据分析，以实现对电力录波数据进行直观的图形或列表化显示，帮助我们对保护动作情况形成全面、完整、客观的判断。

现有电力系统录波数据分析软件的分析功能虽然已经比较丰富，基本上实现了包括谐波分析、相/序量分析、阻抗分析、功率分析、功角分析、频率分析、差流分析、矢量图分析等分析功能，能满足用户的一般需求，但这些分析功能有一个共同缺点，用户参与仅限于有限的参数设置与一定数量的通道选择，而对于电力系统专家级需求的电力系统录波分析，这些分析功能远远不够，他们往往要求更复杂的分析功能。鉴于此，本文基于算术逆波兰算法实现了一种电力录波数据分析公式编辑器，以满足专家级用户对电力录波数据更复杂的分析要求。

1 设计思路

1.1 表达式

表达式，是由数字、运算符、数字分组符号（括号）、自由变量和约束变量等以能求得数值的有意义排列方法所得的组合。约束变量在表达式中已被指定数值，而自由变量则可以在表达式之外另行指定数值。例如，表达式x/y中，自由变量x和y可分别在表达式之外指定值，如x=10和y=5。

1.2 逆波兰表达式

把变量和数字都看作操作数（Operand），同时数字分组符号看作运算符（Operator），表达式则可看作一般由操作数和运算符组成，例如算术表达式中，通常把运算符放在两个操作数的中间，例如a+b，为中缀表达式。波兰数学家Jan Lukasiewicz提出了另一种数学表示法，它有两种表示形式：把运算符写在操作数之前，称为波兰表达式（Polish Expression）或前缀表达式（Prefix Expression），如+ab；把运算符写在操作数之后，称为逆波兰表达式（Reverse Polish Expression）或后缀表达式（Suffix Expression），如ab+。

1.3 本文中的公式编辑器表达式

本文中的公式编辑器基于算术逆波兰算法实现，将用户按照一定规则编写好的复杂的公式交由分析软件来检查执行并显示运算效果的一种有效算法。通过该算法，用户可以实现对指定通道及数据的复杂运算，以更好地对电力系统录波数据进行分析，得出想要的结果。

2 本文中的公式编辑器实现

本文中的公式编辑器执行分为三步。

第一步，将编写好的公式代人相应的通道变量值，转换为普通的中缀表达式；第二步，将第一步转换好的普通中缀表达式转换为逆波兰表达式（后缀表达式）；第三步，转换好的逆波兰表达式求值。

2.1 将编写好的公式转换为普通的中缀表达式

从左到右扫描编写好的公式，如果发现Freq（频率偏差）、EFFV（有效值）、Dist（信号畸变）、Phase（相位差）、IMP_M（阻抗幅值）、IMP_P（阻抗相位）、P（有功功率）、Q（无功功率）、HARM_M（谐波幅值）、HARM_P（谐波相位）、Shift（相移）、正序、负序、零序、突变量运算符和Sum（求和）、Avg（求平均）、Abs（绝对值）、Sin（正弦）、Cos（余弦）、Sqrt（开方）等变量，直接获取对应通道或数字，计算出相应值，将计算出的值替换掉公式中对应部分变量字符串，并继续对替换后的公式进行从左到右扫描直到结束，获得替换后的表达式即为第二步中作为输入的普通中缀表达式，如图1：

2.2 将普通的中缀表达式转换为后缀表达式

1.首先构造一个运算符栈，此运算符在栈内遵循越往栈顶优先级越高的原则。

2.读人第一步中得到的中缀表达式。

3.从左至右扫描该中缀表达式，从第一个字符开始判断，如果该字符是数字，则分析到该数字串的结束并将该数字串直接输出。

4.如果不是数字，该字符则是运算符，此时需比较优先级关系，做法如下：

将该字符与运算符栈顶的运算符的优先关系相比较。如果该字符优先关系高于此运算符栈顶的运算符，则将该运算符人栈；倘若不是的话，则将栈顶的运算符从栈中弹出，直到栈顶运算符的优先级低于当前运算符，将该字符人栈。

5.重复上述操作1-4直至扫描完整个中缀表达式，确定所有字符都得到正确处理，我们便可以将该中缀式转化为逆波兰表达式（后缀表达式）。

图2为将普通的中缀表达式转换成逆波兰表达式的流程图，图中Si为扫描中缀表达式的临时字符变量，re为转换结果输出串，sk为临时栈。

2.3 逆波兰表达式求值

第三步，逆波兰表达式求值。

将第二步转换得到的逆波兰表达式作为本步的计算表达式。

1.首先构造一个运算符栈。

2.从左向右扫描第二步转换得到的逆波兰表达式。

3.如果扫描的项目是操作数，则将其压人操作数堆栈，并扫描下一个项目。

4.如果扫描的项目是一个二元运算符，则对栈的顶上两个操作数执行该二元运算符。

5.如果扫描的项目是一个一元运算符，则对栈的最顶上操作数执行该一元运算符。

6.将运算结果重新压人堆栈。

7.重复步骤2-6，堆栈中即为结果值。

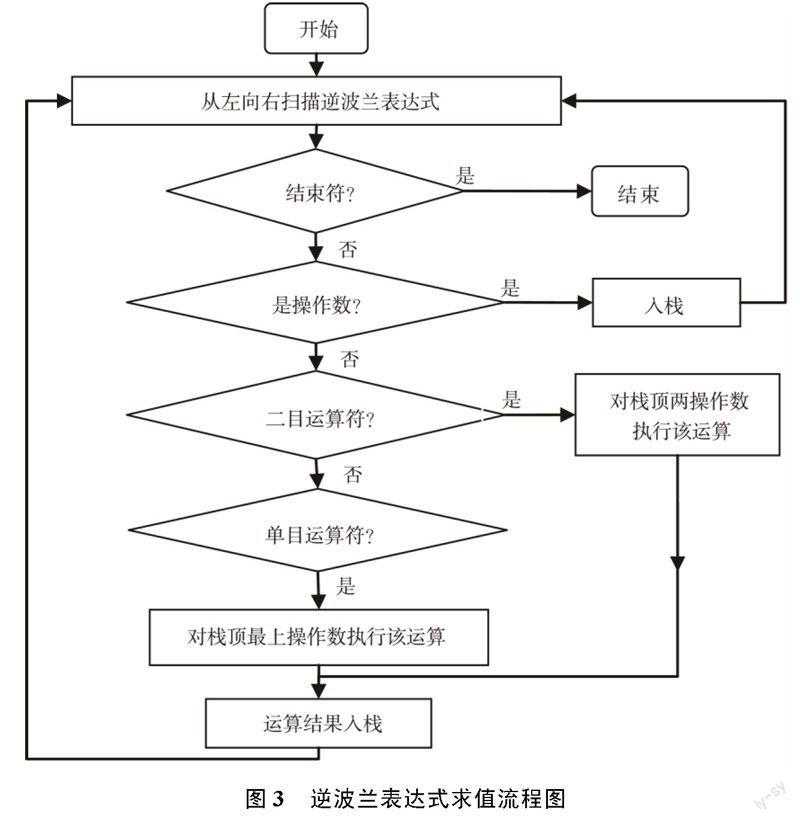
图3为逆波兰表达式求值流程图，即2-6执行过程流程图。

3 公式编辑器应用

3.1 应用领域

本文实现的公式编辑器可应用于电力系统录波数据分析软件，以实现高端用户对于电力录波数据的较复杂的分析需求，对电力系统录波数据分析具有重大意义。可以让用户自己动手编写运算公式，通过按钮选择或手动输入实现对任意符合条件的通道进行包括Freq（频率偏差）、EFFV（有效值）、Dist（信号畸变）、Phase（相位差）、IMP_M（阻抗幅值）、IMP_P（阻抗相位）、P（有功功率）、Q（无功功率）、HARM_M（谐波幅值）、HARM_P（谐波相位）、Shift（相移）、正序、负序、零序、突变量等通道运算或加、减、乘、除、Sum（求和）、Avg（求平均）、Abs（绝对值）、Sin（正弦）、Cos（余弦）、Sqrt（开方）等算术运算以及混合运算，公式编写完成后，首先通过检查按钮进行公式正确性检查，检查通过后则可通过执行按钮经过逆波兰算法实现公式计算的三部算法计算每个点的值，将运算结果生成新的指定类型的通道并在分析波形显示界面显示其波形，编写的公式还可以存储到本地磁盘，以备以后随时调用编辑，或直接执行。

3.2 应用实例

笔者将本文实现的公式编辑器应用于公司的电力系统录波数据分析软件，在公式编辑窗口提供了便捷的Freq（频率偏差）、EFFV（有效值）、Dist（信号畸变）、Phase（相位差）、IMP_M（阻抗幅值）、IMP_P（阻抗相位）、P（有功功率）、Q（无功功率）、HARM_M（谐波幅值）、HARM_P（谐波相位）、Shift（相移）、正序、负序、零序、突变量和加、减、乘、除、Sum（求和）、Avg（求平均）、Abs（绝对值）、Sin（正弦）、Cos（余弦）、Sqrt（开方）等实用按钮，从用户反馈信息来看，实用效果满足高端用户对于电力录波数据的较复杂的分析需求，对电力系统录波数据分析具有重大意义。图4为基于本文实现的公式编辑器实现的电力录波数据分析系统公式编辑器编辑界面。

4 结束语

本文基于逆波兰算法构建了一种实用的电力录波数据分析公式编辑器，并将其应用于软件产品研发。经实践证明，该公式编辑器的实现丰富了电力录波数据的分析功能，满足了专家级用户对于电力录波数据的复杂分析需求，对电力系统录波数据分析具有重大意义，是继电保护装置平稳运行不可或缺的得力助手，进而为电网稳定运行保驾护航。

当然，本文实现的公式编辑器还具有一定的局限性，例如只能对有限的运算符进行运算，需要在使用和实践中不断完善。