基于网络编码的衰落信道频谱感知算法*
郑诗庭,蒙云番邢 杰万海斌覃团发**
(1.广西大学 计算机与电子信息学院,南宁 530004;2.广西大学 广西多媒体通信与网络技术重点实验室培育基地,南宁 530004;3.广西大学 广西高校多媒体通信与信息处理重点实验室,南宁 530004)
1 引言
随着无线通信技术的发展,人们对频谱资源的需求急剧增加,而频谱资源是有限的,因此频谱供需矛盾日益突出。然而,频谱资源的短缺并不是因为频谱资源本身的缺少,而是因为当前采用固定的频谱分配方式造成频谱资源的浪费。根据美国联邦通信委员会统计,一些频段非常拥挤,而部分频段却时常空闲,世界平均频谱利用率仅为15%~85%[1],造成了极大的频谱浪费。在这样的背景下,Mitola等人[2]于1999 年提出了认知无线电(Cognitive Radio,CR)技术。认知无线电网络中,次用户(Secondary User,SU)通过频谱感知技术监测无线环境,利用感知到的空闲频谱进行通信,有效提高频谱利用率。因此,SU 检测频谱忙/闲状态转换的能力十分重要。
频谱感知是认知无线电的关键技术,许多学者对频谱感知展开了研究[3],目前主要有能量检测[4]、循环平稳特征检测[5]、匹配滤波器检测[6]等技术。各感知技术各有自身的优缺点,可根据实际环境选用。其中能量检测算法实现相对简单,检测速度快,无需知道检测信号的先验信息,因此成为研究最广泛的频谱感知算法之一,但该算法易受衰落信道影响。针对能量检测算法易受衰落信道环境影响的缺点,Digham 等人[4]提出了多径衰落信道下的能量检测算法;孙梦巍[7]等人提出了动态时变衰落信道下的频谱感知算法;Lifeng Lai 等人[8]提出了在一定的虚警概率下最小化检测时延的累积和能量检测(Cumulative Summation,CUSUM)算法;Hanafi 等人[9-10]进一步讨论了CUSUM 算法在不同衰落信道下的性能比较,验证了CUSUM 算法抗衰落能力差的特点,并提出了引入多天线以实现在Gaussian 信道及Rayleigh 信道下减小检测时延。许多学者在频谱状态快速检测算法的研究上取得了丰富成果,但在传统的CR 网络中,数据包传输具有随机性和零散性,导致频谱状态转换频繁,检测性能不佳[11]。
针对上述问题,Wang 等人[12]提出将网络编码[13-14]引入CR 网络的主用户(Primary User,PU)信道中,通过随机线性网络编码(Random Linear Network Coding,RLNC)的整形作用使频谱结构化,提高频谱预测性;2014 年,Fanous 等人[11]研究了基于RLNC 的可靠频谱感知和机会式接入算法,提高了系统吞吐率。然而,以上算法没有考虑检测时延和衰落环境的影响,实用性比较差。
本文从减小检测时延、提高系统吞吐率的角度出发,提出了基于RLNC 的快速频谱感知算法,使SU 更容易检测到频谱状态的转变,减小检测时延,提高系统吞吐率。此外,通过推导得到Gaussian、Rayleigh、Rician、Nakagami-m 和F 五种衰落信道下检测信号的概率密度函数及对数似然比,进一步讨论提出的算法的抗衰落能力。
2 系统模型
本文系统模型[12]如图1 所示,一个CR 网络包含N个PU 信道和M个SU,其中每个PU 信道由一个PU 基站(Base Station,BS)和L个PU 接收节点构成一个PU 子网络。在每个PU 子网络中,BS 以速率λ 接收数据包,并依次广播给各PU 接收节点。SU 通过频谱感知算法检测PU 信道并利用空闲频谱传输数据。假设各信道时间同步,一个数据包传输的时间为一个时隙。在每个时隙开始时,SU 随机选择一个信道感知并判断该信道状态。
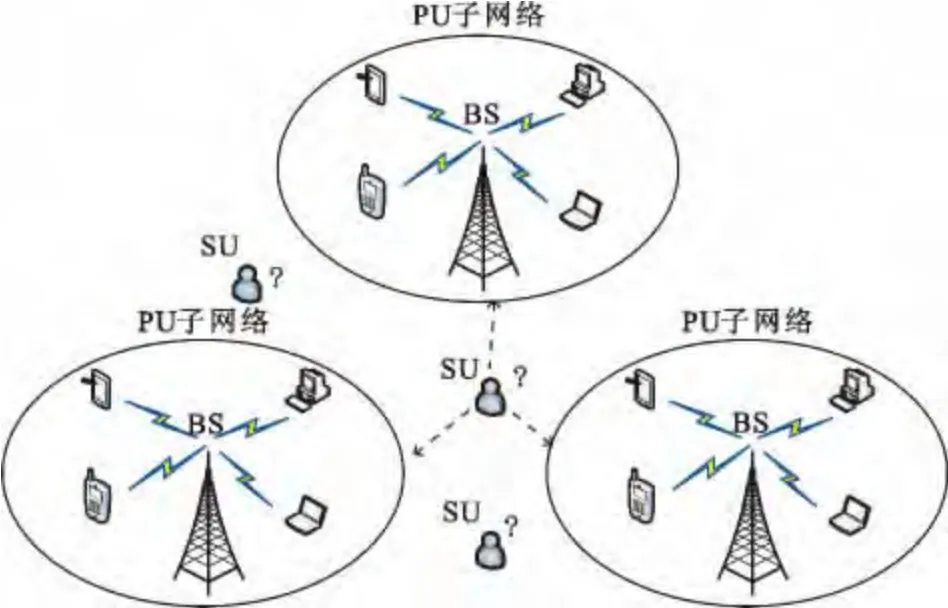
图1 CR 网络模型Fig.1 A CR network model
2.1 主用户传输方式
在传统的CR 网络中,PU 采用自动重传请求(ARQ)传输方式,即:BS 将接收到的数据包缓存并依次广播,每当BS 广播一个数据包,BS 将不断重传该数据包直至所有PU 接收节点都接收到该数据包为止,然后再发送下一个数据包[12]。在该传输方式下,PU 忙/闲状态转换频繁,不易产生频谱空洞,SU也不易检测到频谱状态的转换。此外,由于PU 数据包传输的随机性和零散性,SU 必须不断检测才能保证SU 对PU 状态的及时检测,能耗较大。
针对以上问题,在PU 传输过程中引入RLNC,BS 不仅进行数据的存储-转发,还对接收到的数据包进行编码再传输,提高系统吞吐率[11]。另外,利用RLNC 的频谱整形作用[12],使频谱状态趋于结构化和规律化,有利于产生可利用的频谱空洞,因此SU 也更容易检测到空闲频谱,提高SU 的吞吐率。此外,SU 根据PU 状态转换的规律性进行频谱检测,无需时刻检测,降低能耗。如图2 所示,引入RLNC,当编码块大小为k 时,PU 的忙时段至少为k时隙,闲时段取决于BS 对k个数据包进行缓存编码的过程,PU 忙/闲状态相对于引入RLNC 之前转换稀疏,具有很好的预测性。
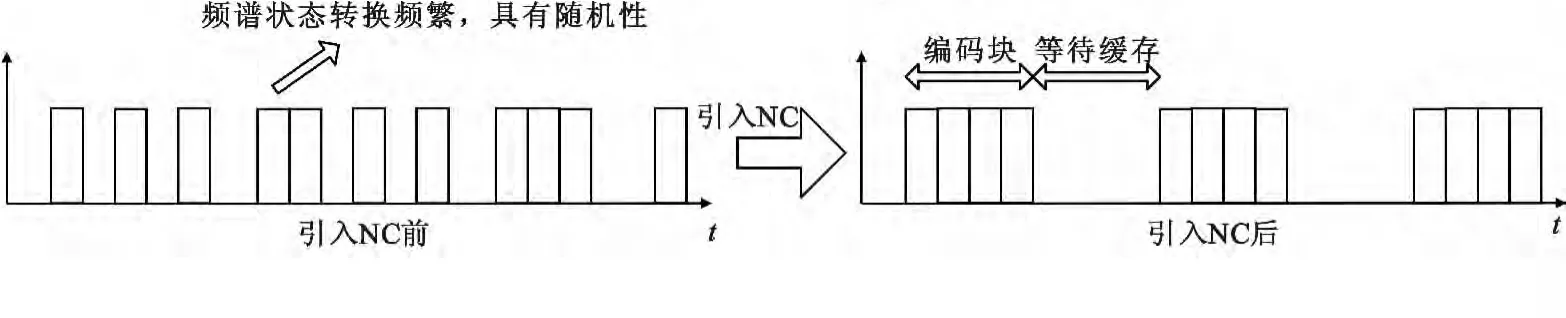
图2 引入RLNC 前后的频谱结构比较图Fig.2 The comparison of spectrum structures with and without RLNC
RLNC 引入到CR 网络的PU 信道中具体实现过程请参见文献[12]。
2.2 信道感知模型
在每个时隙开始时,SU 选择一个PU 信道进行感知。在每个时隙中,SU 检测t个样本。令Y[i]表示SU 检测到的第i个样本,H[i]是信道系数,S[i]是PU 信号,N[i]是噪声,并将SU 检测到的PU 信道状态模型[10]表示如下:
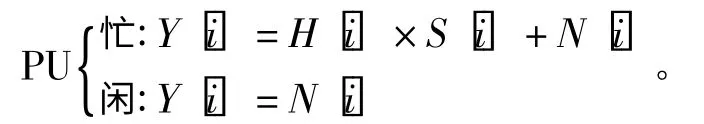
式中,S[i]和N[i]为不相关循环对称复高斯随机变量,即,且,因此信噪比SNR=
假设H1表示该时隙为忙时隙,H0表示闲时隙,一个时隙中的检测序列为Y={Y[1],Y[ 2],…,Y [t]},SU 根据检测结果Y 判断时隙状态[8]:
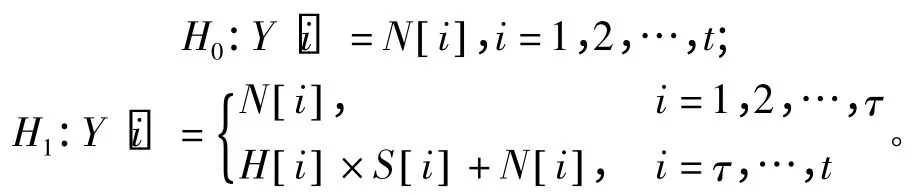
即PU 状态在某一时刻τ 变为忙状态。又假设SU 在时刻ta发出PU 信号存在的警告,若ta>τ,则存在检测时延tdelay=ta-τ;反之,若ta<τ,则发生虚警。然而,检测时延和虚警都对系统用户产生较大的影响,因此本文通过引入RLNC 实现在一定的虚警概率下频谱忙/闲状态的快速检测,减小检测时延。
3 算法描述
针对传统CR 网络中PU 频谱状态转换频繁、频谱结构随机性大、SU 不易检测频谱状态转换和检测时延大等特点,在PU 子网络中引入RLNC,利用RLNC 的整形作用,使频谱结构化,减小检测时延,提高频谱的预测性及可利用性。首先,设计引入RLNC 前后频谱利用率相同的频谱模型;其次,基于该频谱模型设计基于RLNC 的快速频谱感知算法;最后,建立不同衰落信道模型,讨论该算法的抗衰落性能。
实验中,令数据包到达 BS 的速率 λ=0.5 packet/slot,则在PU 子网络中引入RLNC 后,频谱忙/闲时段分别为
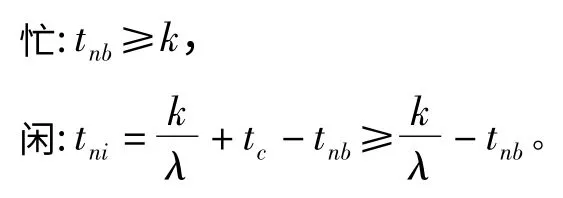
式中,tc为编码时间。为了简化模型,假设PU 信道为理想信道,需要k 次传输传送k个编码数据包,则忙时段正好为k个时隙,闲时段也为k 时隙,信道利用率为50%。而PU 采用ARQ 传输方式时,忙/闲状态每隔一个时隙转换一次,频谱利用率也为50%。
3.1 CUSUM 算法
本文采用CUSUM 算法[8]进行频谱状态转换的检测:假设分别表示PU 忙/闲状态下检测信号Y[i]的概率密度函数(PDF),PU 信号在第τ个样本出现,而SU 在第ta=inf(n:Cn≥h)个样本发出PU 存在的警告,因此若ta≥τ,则ta-τ 为检测时延;若ta<τ,则出现虚警。其中h 为检测阈值,Cn为CUSUM 能量统计量,可由下式得到:
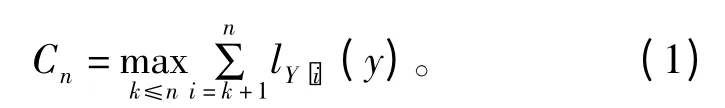
式中,lY[i](y)=,公式(1)又可表示为
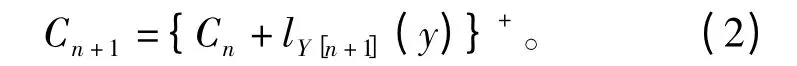
式中,x+=max (x,0) 。令C0=0,当n≥0 时,可通过公式(2)迭代计算得到CUSUM 统计量。当Cn≥h时,则发出PU 存在的警告。
以上是检测PU 忙状态的过程,而检测频谱空洞的过程可同理推出,这里不再赘述。
3.2 基于ARQ 的CUSUM 算法
当PU 采用ARQ 的传输方式,BS 将接收到的数据包缓存并依次广播。当BS 传输一个数据包时,BS 必须不断重传直至所有接收节点都收到该数据包。在该传输方式下,频谱状态转换频繁且具有随机性。因此,基于ARQ 的CUSUM 算法必须时刻监测PU 信道,即:当SU 检测到PU 信道为忙状态,必须继续检测闲状态;同样,当检测到PU 信道为闲状态,也必须立刻开始检测忙状态。该算法耗费能量较大,PU 状态转换频繁,检测时延较大,吞吐率低。
3.3 基于RLNC 的CUSUM 算法
基于RLNC 的整形作用,频谱结构具有一定的预测性。在本文的频谱模型中,引入RLNC 后忙/闲时段均为k 时隙。根据这个结构特性,提出基于退避的频谱感知算法:
步骤1:初始化数据:i 表示检测的第i个样本,初始值为i=0;Cn为检测忙状态时的能量统计量,初始值为C0=0;Sn为检测闲状态时的能量统计量,初始值为S0=0;
步骤2:检测频谱初始状态,如图3 所示。其中:
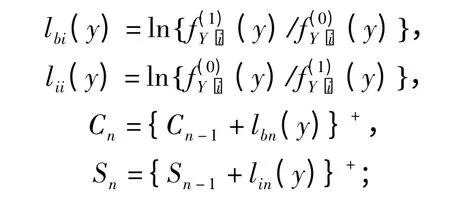
步骤3:根据初始状态判断下一步操作,如图3所示。若频谱初始状态为忙,则退避k 时隙后进入检测闲状态算法;若频谱初始状态为闲,则退避k 时隙后进入检测忙状态算法;
步骤4:当检测到PU 频谱状态为忙时,退避k时隙后再对该PU 信道进行闲状态检测,如图4 所示;当检测到PU 频谱状态为闲时,则退避k个时隙后再对该PU 进行忙状态的检测,如图5 所示;
步骤5:分别得到检测忙/闲状态时的检测总时延。
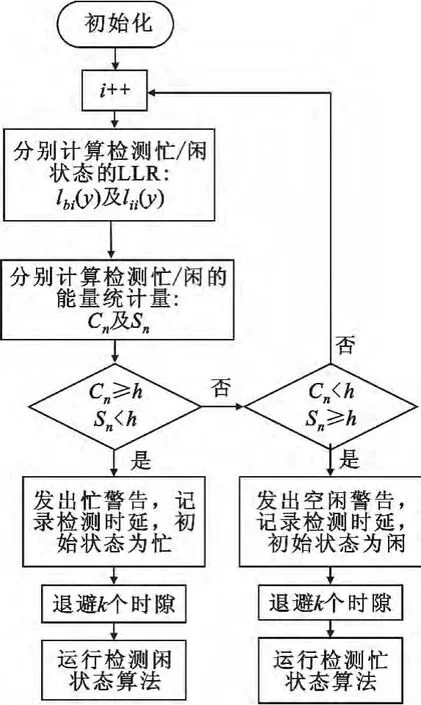
图3 检测初始状态算法Fig.3 Flowchart of the initial state detection algorithm
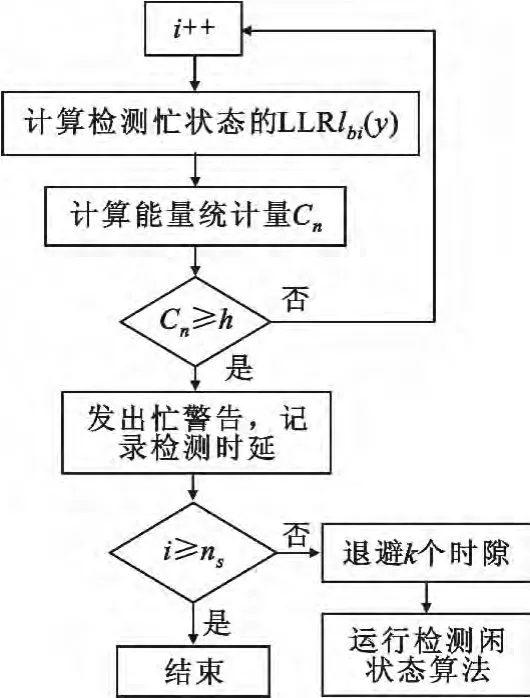
图4 检测闲状态算法Fig.4 Flowchart of the idle state detection algorithm
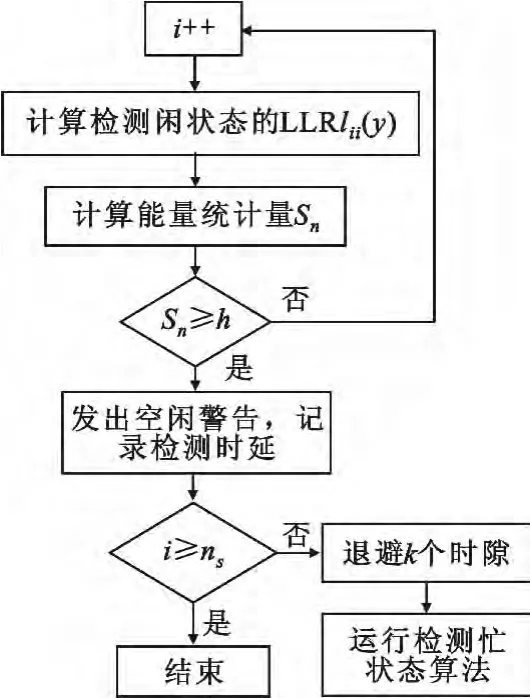
图5 检测忙状态算法Fig.5 Flowchart of the busy state detection algorithm
3.4 不同衰落信道模型
由于SU 接收到的信号在不同的衰落信道中受到不同程度的衰落,在传统的CUSUM 算法中,检测性能受到较大的影响,因此通过比较基于RLNC 的CUSUM 算法在Gaussian、Rayleigh、Rician、Nakagami-m 和F 五种衰落信道下的检测时延及吞吐率,进一步研究该算法的抗衰落性能。下面介绍各衰落信道下的PDF 及LLR。
当PU 信号不存在时,SU 检测到的信号均为噪声,与PU 信号无关,因此PU 不存在时各衰落信道下检测信号的pdf 相同[10],即
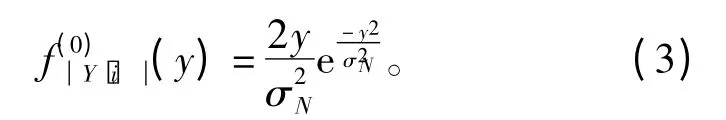
根据文献[10]中的信道模型得到PU 存在时各衰落信道下的PDF 及检测忙状态时的LLR 如下。
(1)Gaussian 信道
PU 存在时检测信号的PDF 为
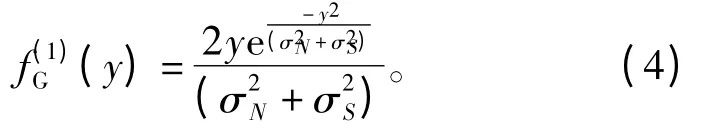
检测忙状态时的LLR 为
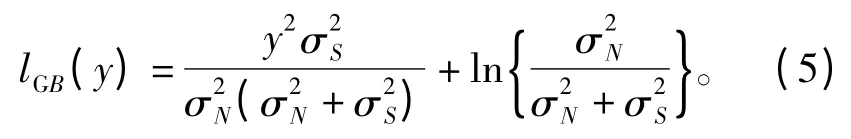
(2)Rayleigh 信道
PU 存在时检测信号的PDF 为
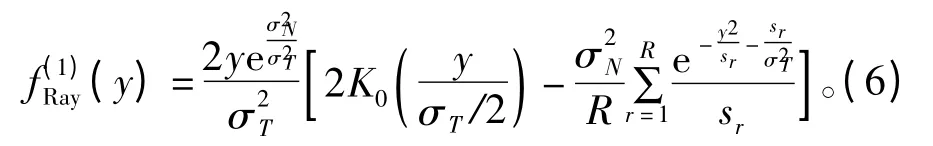
检测忙状态时的LLR 为
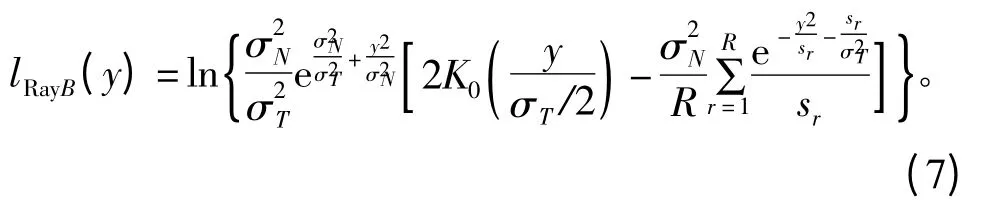
式中,K0(·) 是零阶第二类修正贝塞尔函数;R 为黎曼和中的矩形数,本文设置 R=50;sr=
(3)Rician 信道
PU 存在时检测信号的PDF 为
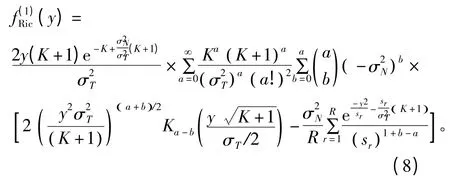
检测忙状态时的LLR 为
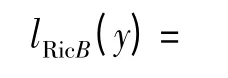
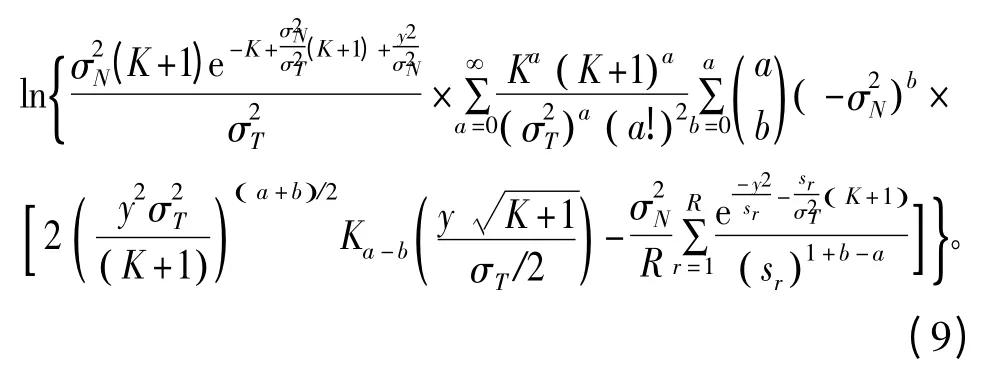
式中,Kv(·) 是v 阶第二类修正贝塞尔函数;K 是Rician 因子,当K=0 时Rician 信道变为Rayleigh 信道,本文采用K=6 dB。
(4)Nakagami-m 信道
PU 存在时检测信号的PDF 为
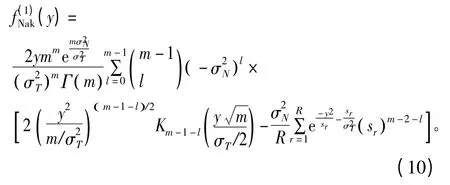
检测忙状态时的LLR 为
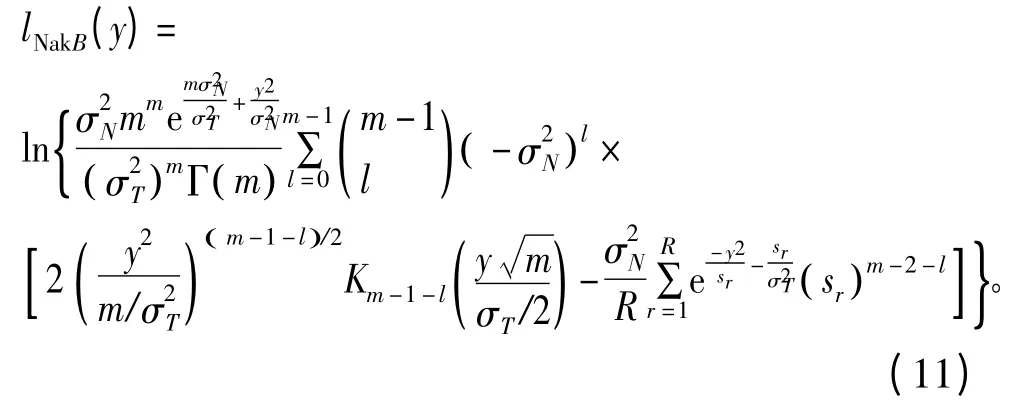
式中,m 是Nakagami 信道的形状因子,表示由多径效应导致的衰落程度,且当m=1/2 时,Nakagami 信道变为单边Gaussian 信道,m=1 时变为Rayleigh 信道,m >1 时和Rician 信道相近,本文采用m=2;Γ(m)是伽马函数。
(5)F 信道
PU 存在时检测信号的PDF 为
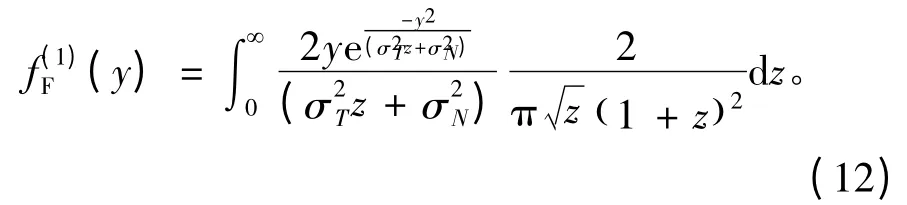
检测忙状态时的LLR 为
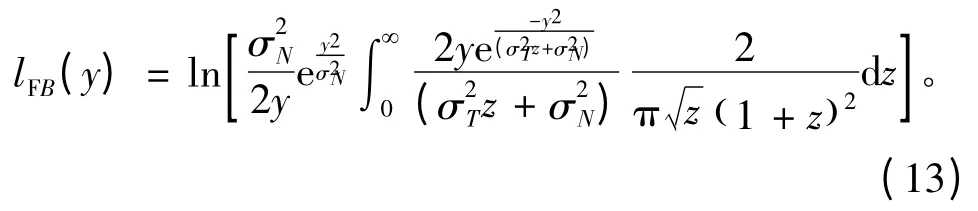
又根据各衰落信道下忙/闲状态的PDF 以及文献[11]中检测空闲状态的CUSUM 算法推导得到检测闲状态时的LLR 如下。
(1)Gaussian 信道
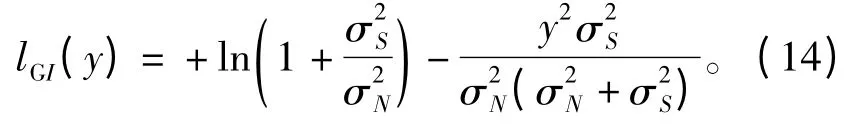
(2)Rayleigh 信道
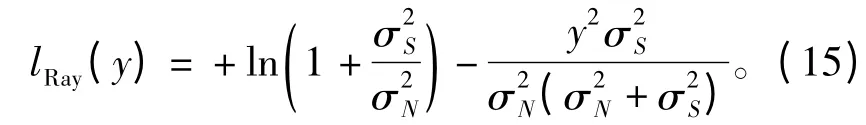
(3)Rician 信道
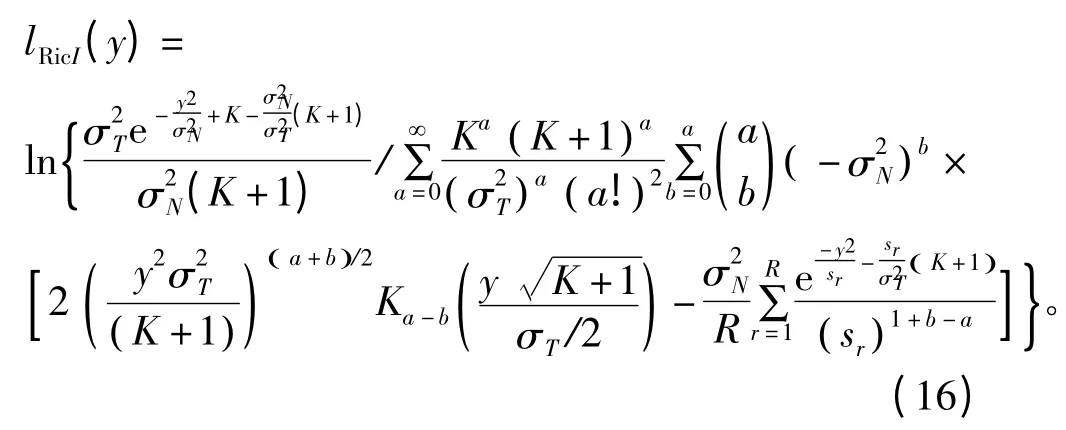
(4)Nakagami-m 信道
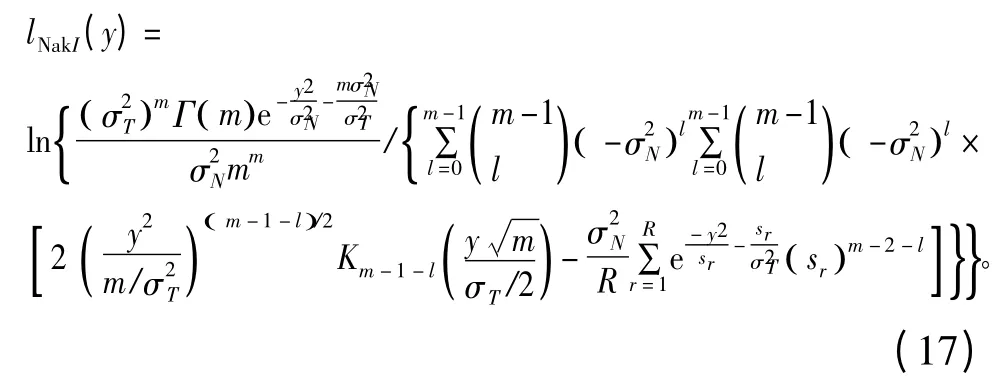
(5)F 信道
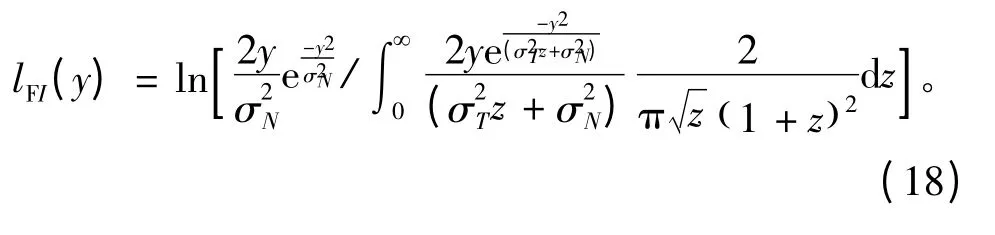
4 实验结果与分析
本节利用MALAB 搭建实验平台对基于RLNC的CUSUM 频谱感知算法的检测性能进行仿真分析,并在Gaussian、Rician(K=6 dB)、Nakagami-2、Rayleigh 和F1,3五种衰落信道下,从检测时延和吞吐率两方面与文献[10]中的检测算法进行比较,讨论本文提出算法的抗衰落性能。
在实验中,五种衰落信道的衰落系数分别为0、0.32、0.36、0.52、1.21,衰落程度逐渐递增,即Gaussian <Rician(K=6 dB)<Nakagami-2 <Rayleigh <F1,3[10]。此外,本文假设,即信噪比为SNR=0 dB;数据包到达BS 的速率为λ=0.5 packet/slot,则引入RLNC 的情况下忙/闲时长分别为tnb=k、tni=k;ARQ 的情况下忙/闲时长分别为tab=1、tai=1,即两种情况下的频谱利用率均为50%。实验对40个时隙进行检测,每个时隙采样20个样本,即总共800个样本。为了提高实验数据的准确性,设置仿真次数为5000。
4.1 检测时延比较
图6 是在Gaussian 信道下引入RLNC 前后的检测时延比较图,其中虚线是基于ARQ 的频谱感知算法,实线是引入RLNC 后的实验结果,分别对应编码块系数k 为2、4、5、10。实验结果表明,基于RLNC的频谱感知算法检测时延大大降低,且随着编码块系数k 的增大而大幅度减小,约为ARQ 的1/k。然而,随着k 的增大,数据包缓存时间亦增加,PU 数据传输时延也相应增加,影响PU 数据传输的及时性,因此编码块系数k 也并不是越大越好,应根据实际需求取得性能均衡。从图中可以看出,当k >4 时,检测时延的降幅逐渐减小,而PU 数据包等待缓存的时间也将大于4个时隙,因此,为了取得SU 检测时延及PU 传输及时性的均衡,本文采用k=4 进行各衰落信道下的检测时延及吞吐率的性能比较。
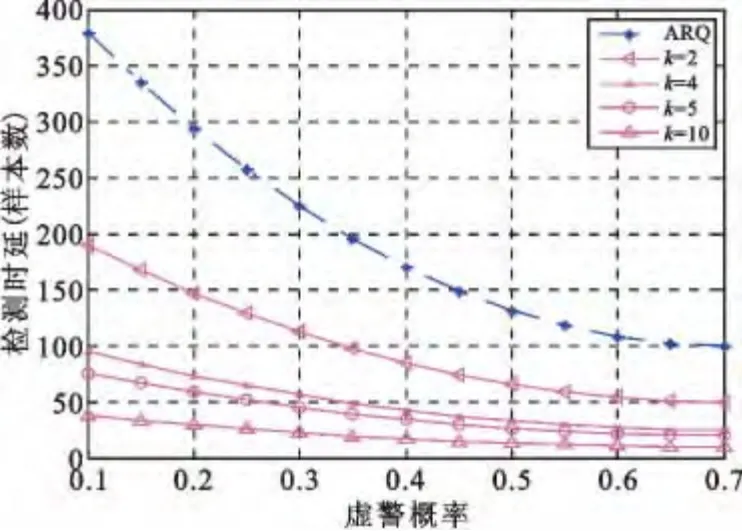
图6 Gaussian 信道下检测时延比较Fig.6 The comparison of detection delay in Gaussian channel
图7 是各衰落信道下引入RLNC 前后的检测时延比较图,其中虚线是引入RLNC 前的算法,实线是引入RLNC 后的算法实现结果。实验结果表明,无论引入RLNC 与否,检测时延均随着衰落系数的增大而增大。然而,通过比较ARQ 及RLNC 的检测时延可知,在基于ARQ 的传统算法中,检测时延受衰落信道影响较严重,而引入RLNC 后,不仅大大降低了检测时延,也提高了其抗衰落能力。
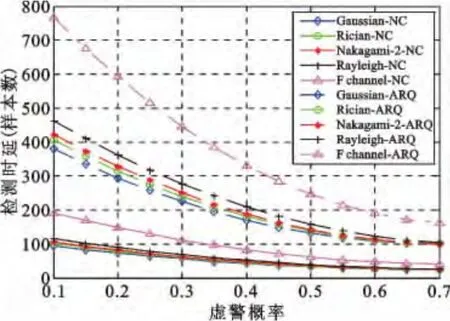
图7 各衰落信道下检测时延比较Fig.7 The comparison of detection delay in various fading channels
4.2 吞吐率比较
图8 和图9 分别是Gaussian 信道下引入RLNC前后的吞吐率比较图,由图中可以看出,引入RLNC有效提高了系统吞吐率。随着编码系数的增大,SU及PU 的吞吐率随着增大,增幅逐渐减小。当k≥4时,吞吐率逐渐接近0.5,增幅非常小,因此,为了均衡SU 检测时延及PU 数据包的传输实时性,取k=4进行进一步讨论。
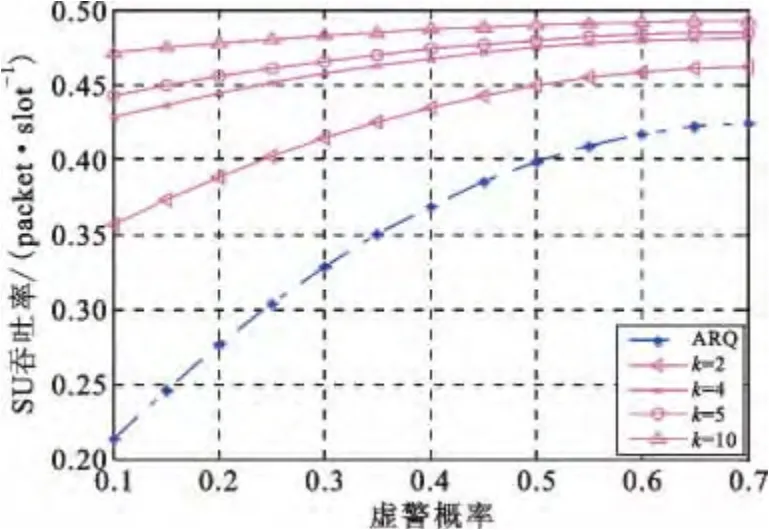
图8 Gaussian 信道下SU 吞吐率比较Fig.8 The comparison of SU throughput rate in Gaussian channel
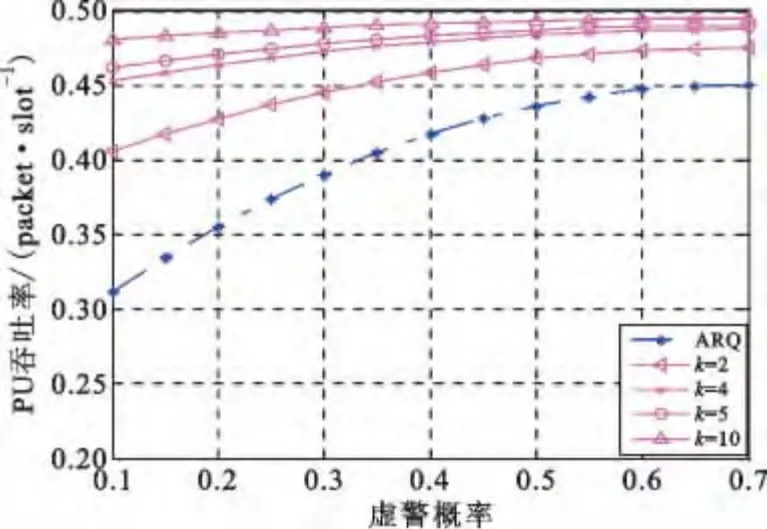
图9 Gaussian 信道下PU 吞吐率比较Fig.9 The comparison of PU throughput rate in Gaussian channel
图10 和图11 分别为各衰落信道下的SU 及PU吞吐率比较图,实验结果表明,随着信道衰落系数的增大,SU 及PU 的吞吐率均随着降低,CV 系数越大,信道衰落越严重,SU 及PU 的吞吐率也越小;但通过比较图中ARQ 及RLNC 的吞吐率可知,从以吞吐率为检验标准的角度来看,引入RLNC 的频谱感知算法具有较好的抗衰落能力。
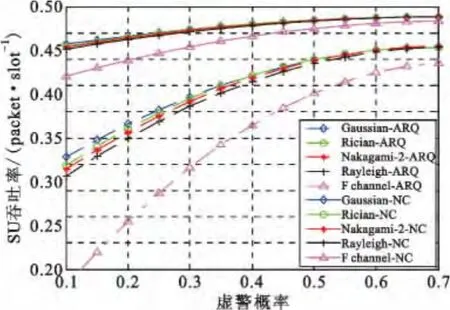
图10 各衰落信道下SU 吞吐率比较Fig.10 The comparison of SU throughput rate invarious fading channels
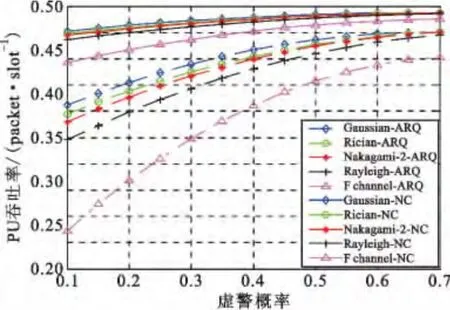
图11 各衰落信道下PU 吞吐率比较Fig.11 The comparison of PU throughput rate invarious fading channels
5 结束语
本文提出了基于RLNC 的CUSUM 算法。该算法在CR 网络的主用户信道中引入RLNC,利用RLNC 的频谱整形作用使随机的、零散的频谱状态结构化,提高频谱结构的规律性及预测性,并基于该规律性及预测性提出退避检测的思想,减小检测时延,提高系统吞吐率。此外,本文针对基于ARQ 的CUSUM 算法抗衰落能力差的特点,通过比较本文提出的算法在Gaussian、Rician(K=6 dB)、Nakagami-2、Rayleigh 和F1,3五种衰落信道下的检测时延和吞吐率,验证了本文提出的算法在降低检测时延、提高吞吐率的同时也具有较好的抗衰落能力,从而使频谱感知技术能够更好地适应复杂的衰落信道环境。然而,RLNC 的引入在提高检测性能的同时,依然存在着不可忽视的安全攻击问题,因此,下一步将重点研究如何提高该算法的安全性。
[1]Federal Communication Commission.Spectrum Policy Task Force Report[R]//ET Docket no.02-155.Washington,DC:FCC,2002.
[2]Mitola J,Maguire G Q.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.
[3]Khan F,Nakagawa K.Comparative study of spectrum sensing techniques in cognitive radio networks[C]//Proceedings of 2013 World Congress on Computer and Information Technology(WCCIT).Sousse:IEEE,2013:1-8.
[4]Digham F F,Alouini M S,Simon M K.On the Energy Detection of Unknown Signals Over Fading Channels[J].IEEE Transactions on Communications,2007,55(1):21-24.
[5]Gardner W A.Exploitation of spectral redundancy in cyclostationary signals[J].IEEE Signal Processing Magazine,1991,8(2):14-36.
[6]Cabric D,Mishra S M,Brodersen R W.Implementation issues in spectrum sensing for cognitive radios[C]//Proceedings of the Thirty- Eighth Asilomar Conference on Signals,Systems and Computers.Pacific Grove,CA:IEEE,2004:772-776.
[7]孙梦巍,赵龙,许巧春,等.动态时变衰落信道下的频谱感知算法[J].通信学报,2014,35(7):63-69.SUN Mengwei,ZHAO Long,XU Qiaochun,et al.New spectrum sensing method under time-variant flat fading channels[J].Journal on Communications,2014,35(7):63-69.(in Chinese)
[8]Lai L F,Fan Y J,Poor H V.Quickest Detection in Cognitive Radio:A Sequential Change Detection Framework[C]//Proceedings of 2008 Global Telecommunications Conference.New Orleans,LO:IEEE,2008:1-5.
[9]Hanafi E,Martin P A,Smith P J,et al.Extension of Quickest Spectrum Sensing to Multiple Antennas and Rayleigh Channels[J].IEEE Communications Letters,2013,17(4):625-628.
[10]Hanafi E,Martin P A,Smith P J,et al.Performance of quickest spectrum sensing over various fading channels[C]//Proceedings of 2013 Communications Theory Workshop(AusCTW).Adelaide,SA:IEEE,2013:69-74.
[11]Fanous A,Sagduyu Y E,Ephremides A.Reliable Spectrum Sensing and Opportunistic Access in Network-Coded Communications[J].IEEE Journal on Selected Areas in Communications,2014,32(3):400-410.
[12]Wang S S,Sagduyu Y E,Zhang J S,et al.The Impact of Induced Spectrum Predictability Via Wireless Network Coding[J].IEEE Transactions on Vehicular Technology,2012,61(2):758-769.
[13]Ahlswede R,Ning Cai,Li S Y R,et al.Network information flow[J].IEEE Transactions on Information Theory,2000,46(4):1204-1216.
[14]孙光昊,覃团发,蒋果生,等.全局编码核加密的弱安全网络编码模型[J].电讯技术,2012,52(12):1974-1979.SUN Guanghao,QIN Tuanfa,JIANG Guosheng,et al.Weakly secure network coding model based on global encoding kernel encryption[J].Telecommunication Engineering,2012,52(12):1974-1979.(in Chinese)

