Tausworthe 非相关均匀随机数的简单生成方法*
张志军,王卫锋,吕丰东,段新涛
(1.河南师范大学 计算机与信息工程学院,河南 新乡 453007;2.智慧商务与物联网技术河南省工程实验室,河南 新乡 453007;3.新乡学院 计算机与信息工程学院,河南 新乡 453000;4.河南师范大学 物理与信息工程学院,河南 新乡 453007)
1 引言
均匀随机数是产生其他分布随机数的基础,例如两个相互独立、取值于(0,1)区间的均匀随机数对,经Box-Muller 变换[1-2]可得到一对相互独立的正态分布随机数。Tausworthe 均匀随机数(Tausworthe Uniform Random Numbers,TURN)序列亦称为线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)序列,由于其硬件易实现且所需硬件资源最少,被广泛用于硬件实现正态分布随机数[3-4]的通信系统蒙特卡洛仿真实验中。
应用于高速通信系统性能硬件蒙特卡洛仿真实验中的TURN 序列生成器,采用的均为和同步脉冲速度一致的并行输出结构[3-4]。针对并行输出相继TURN 间强相关性的问题,研究人员提出了组合Tausworthe 结构[5-6]和一步多跳算法[7-8]等改进算法,这些改进方法均以牺牲硬件资源为代价,并且均未考虑同步产生相互独立均匀随机数对的问题。
本文提出了一个利用不同输出样式以消除相继TURN 间强相关性的方法,在不增添寄存器个数情形下,同时采取不同的、经优化的输出生成矩阵,可并行输出与时钟脉冲速度一致的、能满足蒙特卡洛实验质量要求的非相关TURN 序列对。
2 TURN 序列并行输出结构
TURN 序列生成器基于本原多项式与模2 运算(记为⊕),例如本原多项式为

则对应的LFSR 序列发生器为

式中,系数ck∈{0,1}(k=n-1,n-2,…,0)被称为反馈抽头系数,[cn-1,cn-2,…,c0]是一组不全为0的n 维向量,ck为1 表示LFSR 中第k个寄存器的输出参与反馈有链接,否则无链接。Tausworthe 指出[9],若将上述相继m个随机数作为m 位二进制小数0.XiXi+1… Xi+m-1,则此数可看成区间(0,1)上的均匀随机数,故将此序列称为TURN 序列。显然,经典串行输出TURN 序列的生成速度为LFSR 同步时钟脉冲的1/m。
并行输出结构可提高TURN 的生成速度,其结构如图1 虚线所围部分。设Xt=为两个相继TURN 的m 位量化并行输出序列,显然,随机数Xt+1序列的和随机数Xt序列的是完全一致的,因此,并行输出时,相继TURN 序列间有较强的相关性。图2 给出了生成本原多项式为X52+X3+1[10],并行输出16 量化比特TURN 序列的样本协方差与功率谱密度曲线。理想均匀随机数序列的协方差函数是δ 函数,与之相比,TURN 序列至少有±6 位位移延伸。同时,该均匀随机数序列的功率谱密度中出现不期望的低通特性。
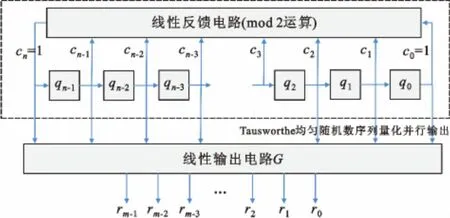
图1 TURN 序列m 比特量化的并行输出结构框图Fig.1 Block diagram of TURN with parallel output structure
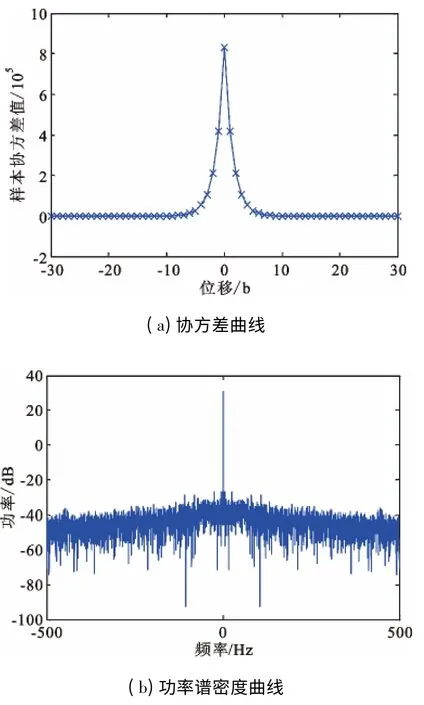
图2 容量为107并行输出TURN序列的样本协方差曲线和功率谱密度图Fig.2 Covariance curve and power spectral density charts for 107 parallel quantified output TURNs
3 TRUN 序列并行输出生成矩阵及其优化
TURN 序列生成器中反馈电路由生成本原多项式完全决定,所生成序列的周期为2n-1,n 为LFSR的阶数。在应用TURN 序列时,希望其周期趋于无穷大,也就是说,LFSR 的阶数n 远大于并行量化比特位数m。因此,每一量化比特ri可由多个寄存器的状态共同决定,这一关系可用输出生成向量gi表示:
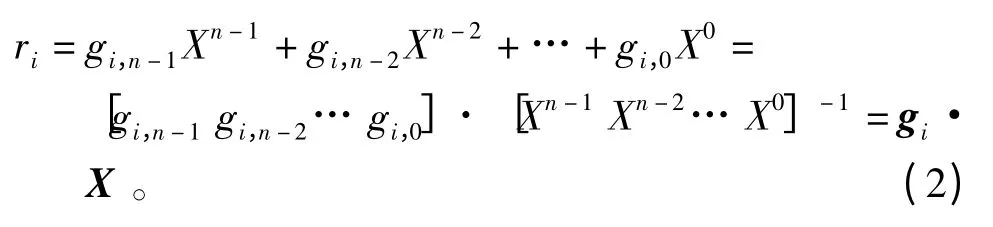
上述加法是模2 加,gi,j∈{0,1}(j=n-1,n-2,…,0)称为生成抽头系数,生成向量gi=[gi,n-1gi,n-2… gi,0]中的gi,j不全为零。设向量重量函数w(gi)表示向量gi中1 的个数。由于gi,j取值为二进制数,在下面描述中向量gi用八进制数表示,例如gi=(15),则该生成向量为[1 1 0 1],w(gi)=4。改进后的TURN 序列并行量化输出结构的位置在图1中以线性输出电路G 示意出。
对于m 位量化输出构成的向量r=[rm-1rm-2…r0],可由生成向量所构成输出生成矩阵表示:

经典TURN 序列m 比特位并行输出时,所对应的输出生成矩阵是稀疏的,其输出生成矩阵为

式中,Im×m为m 阶单位矩阵,当量化输出比特位数m等于LFSR 的阶数n 时,G'退化为n 阶单位矩阵。显然,不同生成矩阵G 生成不同的TURN 序列,因此,非相关TURN 序列并行输出电路结构的设计优化问题可转化成对输出生成矩阵G 的优化问题。
硬件资源的高效利用是TURN 序列生成器设计优化的目标之一,即在随机数质量不下降前提下,以生成矩阵G 中1 的个数尽可能少为优化目标,即
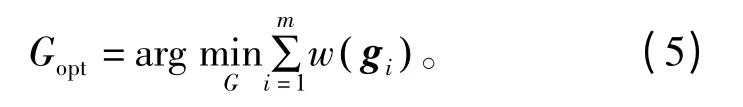
对式(4)中的生成矩阵G 采用差分进化算法[11]进行优化。表1 给出了两组生成矩阵G 的优化参数,其生成本原多项式为X52+X3+1,TURN 序列16 量化位。

表1 生成矩阵G 的两组优化参数Table 1 Optimized parameters of two generator matrices
4 实验结果分析与随机数质量检验
图3 给出了生成矩阵为G1、容量为107改进TURN 序列的样本协方差曲线和功率谱密度。与图2 对比可得,利用本文所提生成方法,采用优化的生成矩阵所生成的TURN 序列相继值间呈现非常理想的低相关性,同时功率谱的低通效应也随即消失。
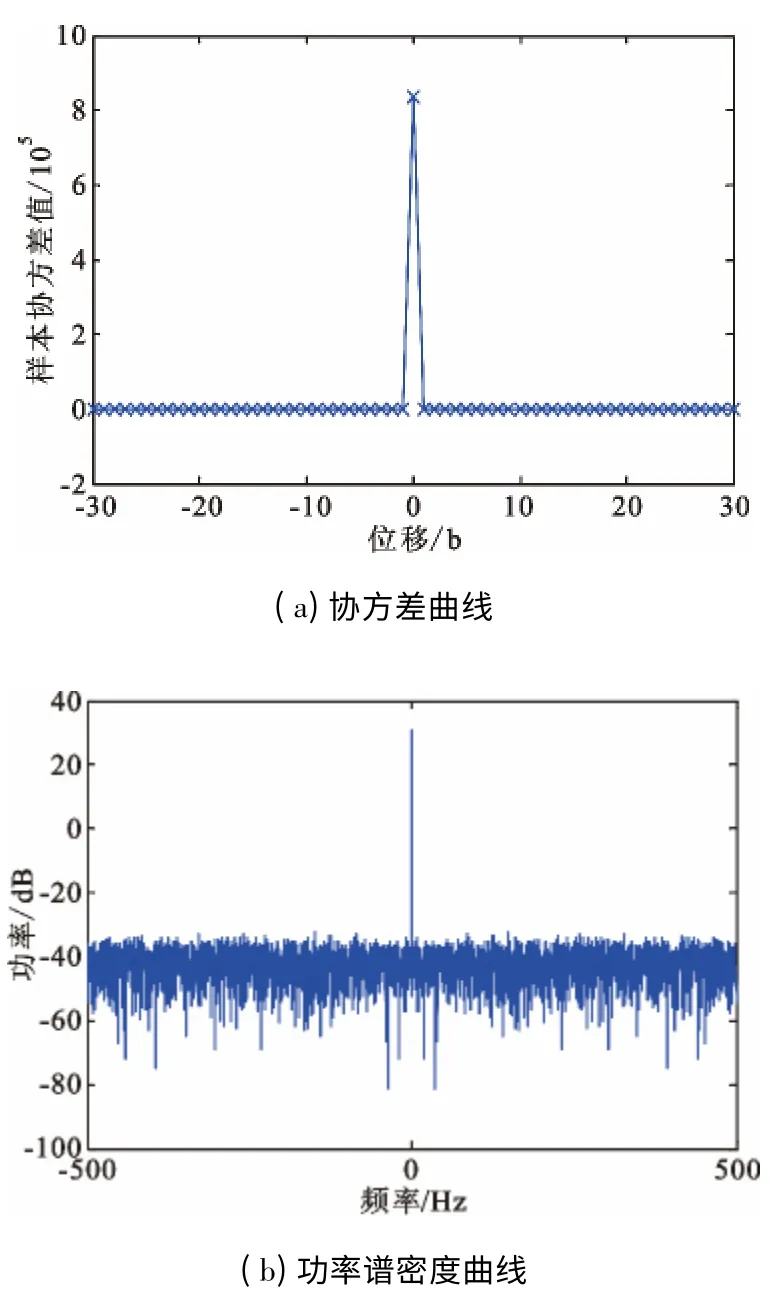
图3 生成矩阵G1所生成的容量为107改进的TURN 样本协方差曲线和功率谱密度图Fig.3 Covariance curve and power spectral density charts for 107 TURNs with optimized output generator matrix G1
4.1 χ2 拟合优度检验
拟合优度检验是一种检验样本数据是否服从某一分布的方法。随机数质量检验中,χ2拟合优度检验[11]是最常用的方法,其检验统计量为
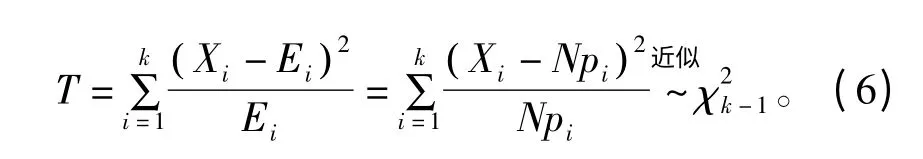
检验时,样本被分割成k个区间,Xi为样本数据落入区间((i-1)/k,i/k)内的观测个数,i=1,2,…,k;Ei为落入该区间待检验分布的期望观测值,对于容量为N 的样本,该值为Npi,pi为待检验变量落入区间((i-1)/k,i/k)内的概率,对于均匀分布假设,pi=1/k。
图4 给出了生成矩阵G1所生成容量为106和107改进TURN 序列的样本直方图,其中k=50,在显著水平α 为0.05 和0.01 下的拒绝域分别为[66.34,+∞)和[74.90,+∞)。

图4 生成矩阵G1所生成容量为106和107的改进TURN样本直方图,检验P-值分别为0.913 5 和0.643 6Fig.4 Sample histograms with P-value 0.913 5 and 0.643 6 for 106 and 107 TURNs with optimized output generator matrix G1
表2 给出了生成矩阵G1和G2在不同容量下样本检验统计量t 值及检验的P-值[11]。从表2 可以看出,生成矩阵为G1和G2、容量分别为106和107改进TURN 序列样本检验统计量t 值均未落入拒绝域,表明均通过χ2拟合优度检验,即生成矩阵G1和G2所生成的样本均可认为是(0,1)区间内的均匀随机数。表2 同时给出了Matlab 软件和ANSI C 标准中,常用均匀随机函数rand()所生成同容量下均匀随机数的统计量t 值和对应的P-值,对比可得,利用优化输出生成矩阵所生成的改进TURN 序列完全可以取代上述两个软件应用于通信系统性能的硬件蒙特卡洛仿真实验中。
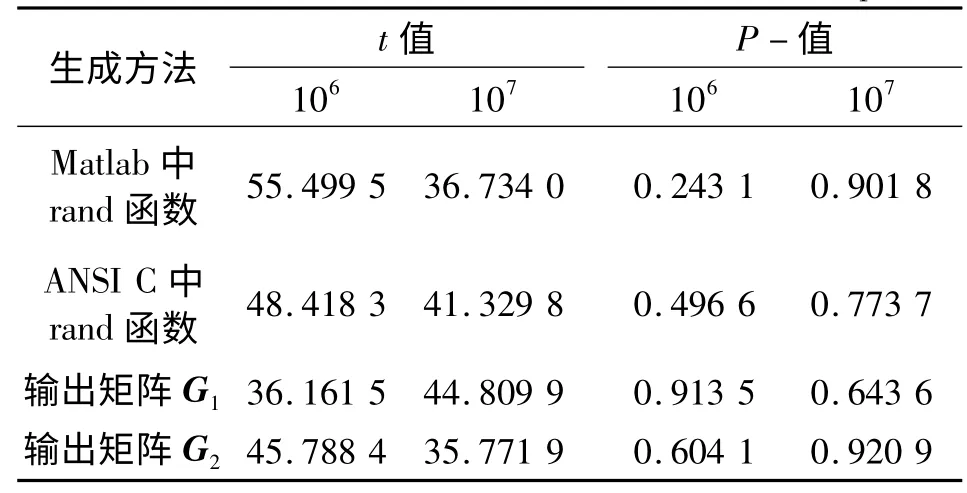
表2 均匀随机数的样本检验统计量t 值和对应P-值Table 2 Test statistic and P- values for different samples
4.2 独立性检验
满足Box-Muller 变换服从(0,1)区间上的均匀随机数对必须不相关,因此,需对所提方案中由不同生成矩阵生成的TURN 序列对进行相关性检测。本文采用样本相关系数进行度量检测,其定义为[11]
相关系数值越小表明随机数对越不相关。从表3 可得,与常用软件生成的均匀随机数对相比,优化的生成矩阵G1和G2所生成的均匀随机数对间完全可以满足非相关性的要求。
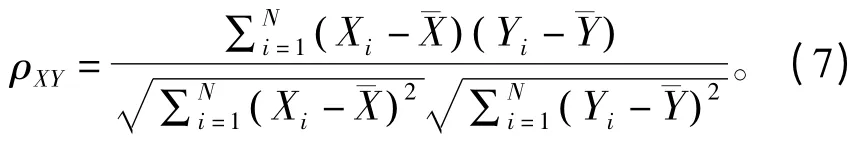

表3 不同容量下各算法生成均匀随机数对的相关系数Table 3 Correlation coefficients for pairs of uniform random numbers generated by different algorithms
利用组合Tausworthe 结构和一步多跳算法生成相互独立的TURN 序列对时,是基于多个同结构、不同初始寄存器状态的TURN 序列生成器并行输出的。与之相比,表3 中改进的TURN 序列对是在不增添寄存器个数前提下,通过配置不同优化的输出生成矩阵所生成的。表4 给出了上述3 种优化算法生成2个相互独立的Tausworthe 均匀随机数时,对应的随机数生成器在Altera Cyclone FPGA 上硬件结果,生成的本原多项式为X52+X3+1,并行16 比特量化位。从表4 可得,利用本文不同优化输出矩阵生成均匀随机数对时,所需的硬件资源仅为组合Tausworthe 结构和一步多跳算法的27.4% 和48.8%,硬件资源的利用效率大大提高,该优势随着输出非相关TURN 序列个数的增多而更趋显著。

表4 各优化算法生成2个非相关TURN 序列所需硬件资源类型(EP1C6Q240)Table 4 Resources to generate two uncorrelated TURNs for different algorithms
5 结束语
数字通信系统性能仿真实验时,均匀随机数序列常用于模拟数字信号源和噪声。加性高斯白噪声信道中服从高斯分布的噪声,通常由独立的均匀随机数序列对经变换得到。本文针对经典TURN 序列并行输出时相继值间呈现较大相关性问题,在应用高周期的TURN 序列生成器中寄存器个数大大增加情形下,提出了一种新的非相关TURN 序列生成方法。该方法中每位输出量化比特均由多个寄存器的状态共同决定,从而将生成TURN 序列问题等价为输出生成矩阵的优化问题。在需要同时输出多个TURN 序列的硬件仿真实验中,与组合Tausworthe结构和一步多跳优化方法基于多个同结构、不同初始寄存器状态的TURN 序列生成器并行输出相比,采用本文所提方法可以根据优化的输出生成矩阵快速配置输出完成,不需要对电路中的反馈电路等其他结构部分进行重新设计,相应的电路仅需增加输出所需的连线和模2 加电路,大大提高了硬件资源的利用率,这是区别于其他TURN 序列优化方法最主要的地方。将本文改进的TURN 序列应用于高斯信道、衰落信道等场景下通信系统性能硬件蒙特卡洛实验中,是后续需要进一步研究的内容。
[1]Malik J S,Hemani A,Malik J N,et al.Revisiting Central Limit Theorem:Accurate Gaussian Random Number Generation in VLSI[J].IEEE Transactions on VLSI Systems,2014,23(5):842-855.
[2]张志军,刘行兵,段新涛.高斯随机数生成算法对比研究[J].河南科技学院学报(自科版),2014,42(3):56-59.ZHANG Zhijun,LIU Xingbing,DUAN Xintao.Algorithm comparison on Gaussian random number generators[J].Journal of Henan Institute of Science and Technology(Natural Sciences Edition),2014,42 (3):56- 59.(in Chinese)
[3]Alimohammad A,Fard S F.FPGA-based bit error rate performance measurement of wireless systems[J].IEEE Transactions on VLSI Systems,2014,22(7):1583-1592.
[4]Yen S W,Hung S Y,Chen C L,et al.A 5.79-Gb/s energy-efficient multirate LDPC codec chip for IEEE 802.15.3c applications[J].IEEE Journal of Solid-State Circuits,2012,47(9):2246-2257.
[5]L'ecuyer P.Maximally equidistributed combined Tausworthe generators[J].Mathematics of Computation of the American Mathematical Society,1996,65(213):203-213.
[6]谷晓忱,张民选.多输出LFSR 结构均匀分布伪随机数生成器的硬件设计优化[J].武汉大学学报(信息科学版),2010,35(5):566- 569.GU Xiaochen,ZHANG Minxuan.Mult- ioutput LFSR Based Uniform Pseudo Random Number Generator[J].Geomatics and Information Science of Wuhan University,2010,35(5):566- 569.(in Chinese)
[7]Li Y,Chow P,Jiang J,et al.Software/Hardware Parallel Long- Period Random Number Generation Framework Based on the WELL Method[J].IEEE Transactions on VLSI Systems,2014,22(5):1054-1059.
[8]Lu Q,Fan J,Sham C,et al.A high throughput Gaussian noise generator[C]// Proceedings of 2014 IEEE Asia Pacific Conference on Circuits and Systems.Ishigaki:IEEE,2014:117-120.
[9]Tausworthe R C.Random numbers generated by linear recurrence modulo two[J].Mathematics of Computation,1965,19(90):201-209.
[10]刘玉君.信道编码[M].修订版.郑州:河南科学技术出版社,2001:30-31.LIU Yujun.Channel Coding[M].revised ed.Zhengzhou:Henan Science and Technology Press,2001:30-31.(in Chinese)
[11]Kroese D P,Taimre T,Botev Z I.Handbook of Monte Carlo Methods[M].New York:John Wiley & Sons,2013:301-345.

