一种考虑传感器精度的数据自适应加权融合算法*
邢晓辰,蔡远文,任江涛,赵征宇
(1.装备学院 研究生院,北京 101416;2.装备学院 航天装备系,北京 101416;3.北京航天飞行控制中心,北京 100094)
1 引言
随着信息处理技术与计算机技术的飞跃发展,多传感器信息融合技术已在遥感探测、智能交通、故障诊断、模式识别等领域受到广泛重视并取得了众多成果。采用多个传感器对同一参数进行测量并融合,能够显著消除传感器自身不确定性与外界干扰噪声带来的消极影响,生成比单一传感器更加准确可信的测试值[1]。其中,基于加权的数据融合方法,在融合过程中无需测量数据先验信息且融合精度高,以具有最优性、无偏性和均方误差最小而受到普遍重视[2-3]。采用加权融合算法的关键,是如何确定各传感器测量数据融合时的权重值。
当前,多传感器测量数据加权融合中的典型算法主要包括算术平均算法、最小二乘加权融合算法、切尾均值融合算法、切尾加权融合算法以及基于距离的自适应加权融合算法。
当传感器工作性能稳定并且所受外界环境干扰可近似忽略不计时,基于传感器初始精度的最小二乘加权融合算法融合效果优于算术平均算法[4-5]。若传感器初始精度未给出,在满足一定条件下可由历史测量数据计算得出,下文将详细分析计算方法。
多源信息融合的优势即有效利用处于不同方位、不同状态的多传感器测试信息,基于信息互补将各传感器所提供的局部、不完整、不确定信息进行融合,形成对待测对象更加全面准确的描述。切尾均值融合算法与切尾加权融合算法均舍弃了部分传感器测量数据,区别仅在于对剩余测量数据融合时所赋权重不同[6]。此两种基于信息丢失性处理的算法造成信息资源的浪费,完全割裂了被丢弃传感器与剩余传感器信息间的内在联系,也削弱了采用多源信息融合的意义。同时,比率的选取主观性较大,实际操作复杂。因此,切尾融合算法并不可取。
基于距离的自适应加权融合算法摒弃了基于测量数据统计特性生成方差的方法,基于各传感器当前测量数据间某种距离生成数据融合权重。此种算法对被测对象状态的变化情况跟踪较好且适应性高,但测量数据间距离生成方式的选取对融合效果影响较大[7-8]。文献[7]选用置信距离作为测量数据间的距离测度,但置信距离形式需要结合具体工程背景设置。文献[8]选用绝对值距离作为距离测度,但该文基于绝对值距离生成数据融合权重时设定了门限值,增加了算法的复杂性,并且二值判定方法也降低了量测值的利用效率。
综上分析,本文采用基于距离的自适应加权融合算法,选取证据理论中的修正证据距离计算传感器测量数据间距离。同时,当传感器初始精度已经给出或者能够计算得出时,计算测量数据融合权重时也应考虑这部分信息。基于此,我们提出一种考虑传感器初始精度的基于距离的多源数据自适应加权融合算法,并通过多种典型算例验证了算法的有效性与强鲁棒性。
2 改进的自适应加权融合算法模型
为有效解决多传感器测量数据融合中的权重值分配问题,综合考虑传感器精度与实际测量数据误差对融合结果的影响,提出一种基于修正证据距离mdBPA的改进自适应加权融合算法。mdBPA在Jousselme 距离定义基础上进行改进,而Jousselme 距离本意用来求解证据融合后生成的决策与真实结果之间的差异度,后来多被研究者用以衡量证据间冲突程度[9]。mdBPA在Jousselme 距离的基础上进行改进,保留了Jousselme 距离良好的数学特性,并解决了其在衡量证据相似性上所存在的问题,收敛性更好[10]。本文将mdBPA引入,用以衡量传感器测量数据间冲突程度,以表征数据间不一致性。其中,mdBPA定义如公式(1)所示:
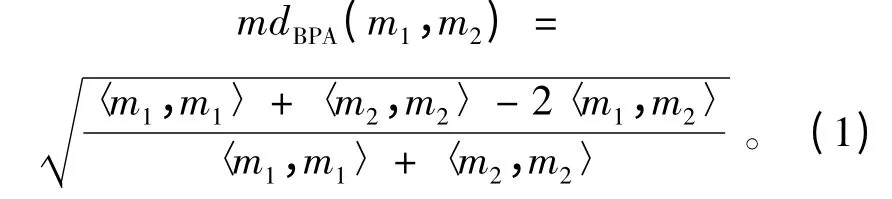
改进的融合算法模型针对三种不同情况分为三个部分:
(1)传感器初始精度已知;
(2)传感器初始精度未知,但可通过实际测量数据计算得出。基于实际测量数据计算传感器精度,需满足以下要求:待测对象状态在较长的一段时间域内基本不发生改变,满足(或近似满足)静态测量条件;用于计算的测量数据个数足够多,通常大于20个;
(3)传感器初始精度未知,也无法通过实际测量数据计算得出。不考虑传感器精度,仅基于实际测量数据进行自适应加权融合。
假设有n个同质传感器对某一对象进行测量(针对异质传感器数据融合需要对测量数据基于某种算法进行数据转换,本文仅考虑同质传感器),n个传感器的初始精度分别为待测对象状态真值为X,各传感器测量数据分别为x1,x2,…,xn,测量数据均值为,融合后估计值为。各传感器均独自完成数据测量,测量数据分布满足相互独立条件。
针对上述三种情况,设计改进的融合算法模型,主要包含以下步骤:
(1)基于mdBPA计算第i个测量数据与第j个测量数据间的距离
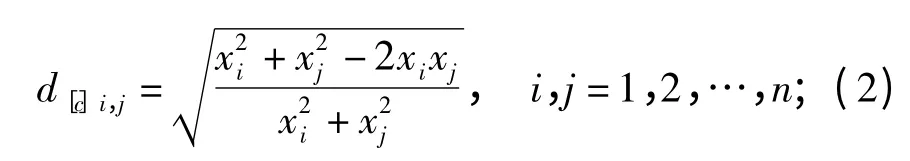
(2)基于d[md]i,j生成第i个测量数据与其余测量数据间的平均距离
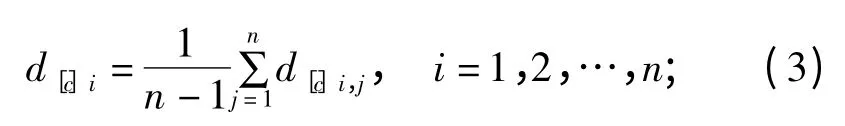
(3)借鉴文献[8]中的支持度变换函数,本文采用公式(4)基于d[c]i计算当前时刻各测量数据参与融合时的测量权重w[c]i。大量实测数据计算证明,变换函数的幂值取为3 时,能够较好地降低野值影响;当变换函数的幂值取更大值时,降低野值的效果增幅作用并不明显,因此公式中变换函数的幂值取为3:
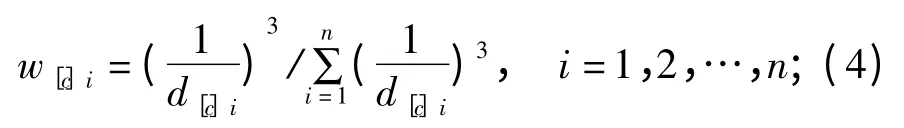
(4)当传感器初始精度已知或者测量精度能够计算时,将测量权重w[c]i与固定权重w[g]i进行综合,生成最终权重wi;当传感器初始精度未知且测量精度无法计算时,测量权重w[c]i即为最终融合权重wi。其中,w[g]i的计算方法将在下文给出。
由于传感器自身性能状态或者外界环境在测量过程中可能会发生较大改变,因此综合两种权重值时以测量权重为主,具体设定可依据实际情况而定。本文将两种权重值的比值设定为1∶ 3,综合后的最终权重wi计算如下:
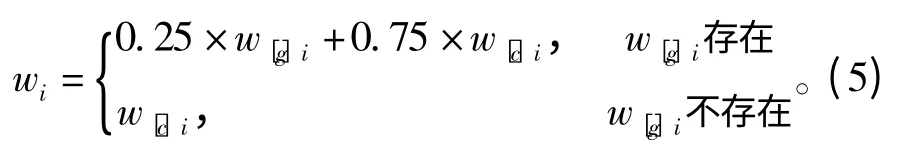
固定权重值w[g]i的计算分为传感器初始精度已知和传感器初始精度未知但满足计算条件两种情况。
对于第一种情况,基于预先给出的传感器初始精度,生成测量数据参与融合时的固定权重

对于第二种情况,针对第i个传感器选取多个历史测量数据xi(j),本文将历史数据个数定为20。其中,i=1,2,…,n;j=1,2,…,20。设20个历史测量数据的均值为,基于xi(j)计算得出该传感器的测量精度,进而计算得出w[g]i:
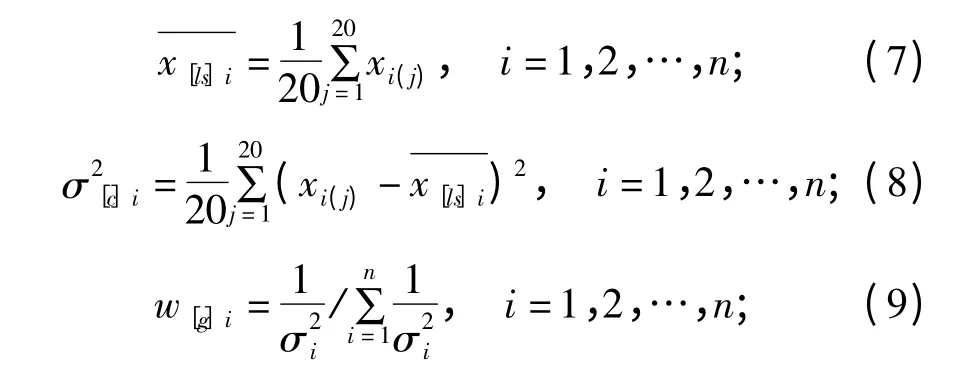
(5)基于wi对当前时刻各测量数据进行加权融合,生成最终融合值
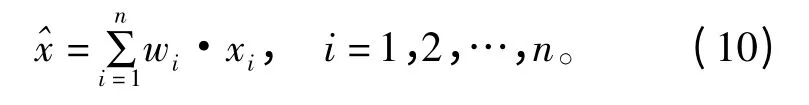
为便于直观理解,本文所设计的改进融合算法流程如图1 所示。
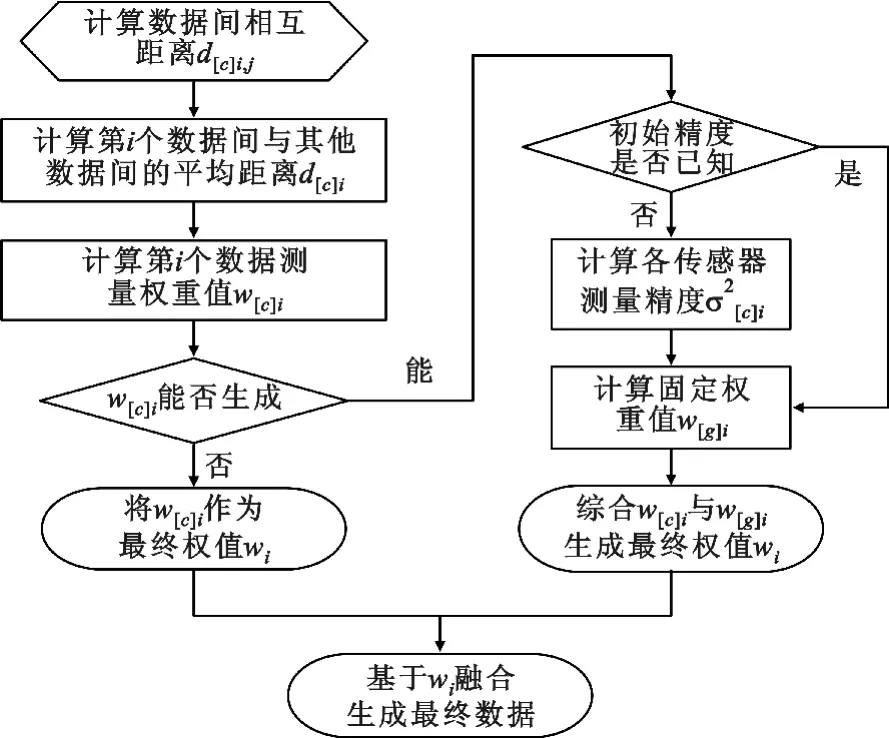
图1 改进的融合算法流程Fig.1 Flow chart of the improved fusion algorithm
3 算例验证
3.1 传感器初始精度已知
假设已知各传感器初始精度,在此条件下对本文算法进行验证。
为验证本文算法对一般性多传感器数据融合的适用性,采用文献[8]中的算例作为本文验证算例。为便于算法间对比分析,将算术平均算法定义为算法1,固定权重值融合算法定义为算法2,文献[8]中不考虑传感器初始精度的算法定义为算法3,考虑传感器初始精度时定义为算法4。算法3 与算法4 的基本思路如下所示:
(1)算法3:计算各传感器测量数据距离di,j,基于di,j计算某测量数据xi到其余测量数据的平均距离,基于计算所有测量数据间相互平均距离,基于计算xi对xj的支持度Si(xj),基于Si(xj)计算门限值Δi,进而生成xj获得的总支持度m(xj),计算得出各传感器测量数据融合权重值wi[jlc],基于wi[jlc]完成数据融合;
(2)算法4:当给定传感器初始精度时,将基于传感器初始精度生成的固定权重值wi[g]与wi[jlc]融合,生成融合后的权重值wi[g-jlc],计算方法如公式(11):
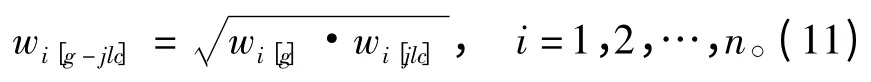
为更全面、合理地验证各算法融合性能,考虑传感器性能正常与部分传感器出现故障两种情况,分别对应设置算例1 与算例2。两种情况下,设各传感器初始精度均为已知,传感器性能均正常时各传
感器初始精度如表1 所示。

表1 各传感器初始精度分配Table 1 Initial accuracy allocation of each sensor
算例1:假设6个传感器均工作正常,其在7个采样时刻的测量值如表2 所示,待测对象真值为50。由表1 可以看出,各传感器从传感器1 到传感器6 精度逐渐降低,因此在传感器正常情况下,各传感器实际测量值相对待测真值的偏差也应逐渐增大,表2 中测量数据与分析相一致。
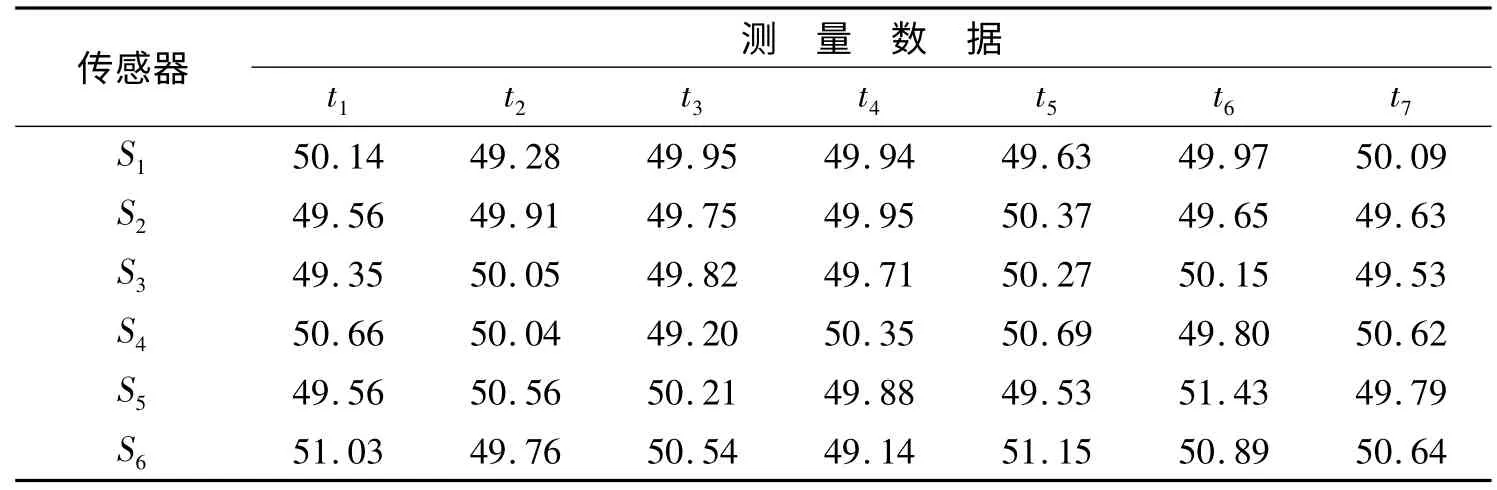
表2 各传感器正常情况下测量数据Table 2 Measurement data under normal condition of each sensor
分别采用算法1、算法2、算法3、算法4 以及本文算法对表2 中各传感器测量数据进行融合,各算法融合结果及融合效果评估如表3 所示。参考文献[8],引入融合结果总体标准偏差与极限偏差Δmax概念,计算方法分别见公式(12)与(13):
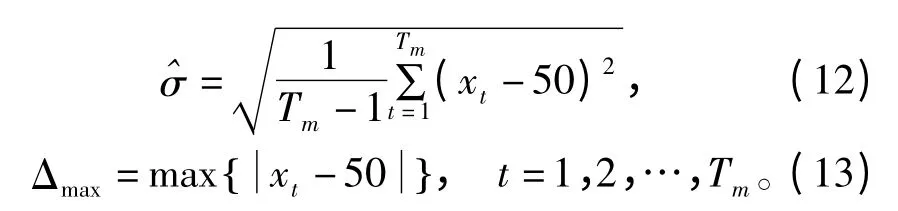
式中,Tm表示采样时刻的次数,xt表示第t 次采样时刻的融合值。
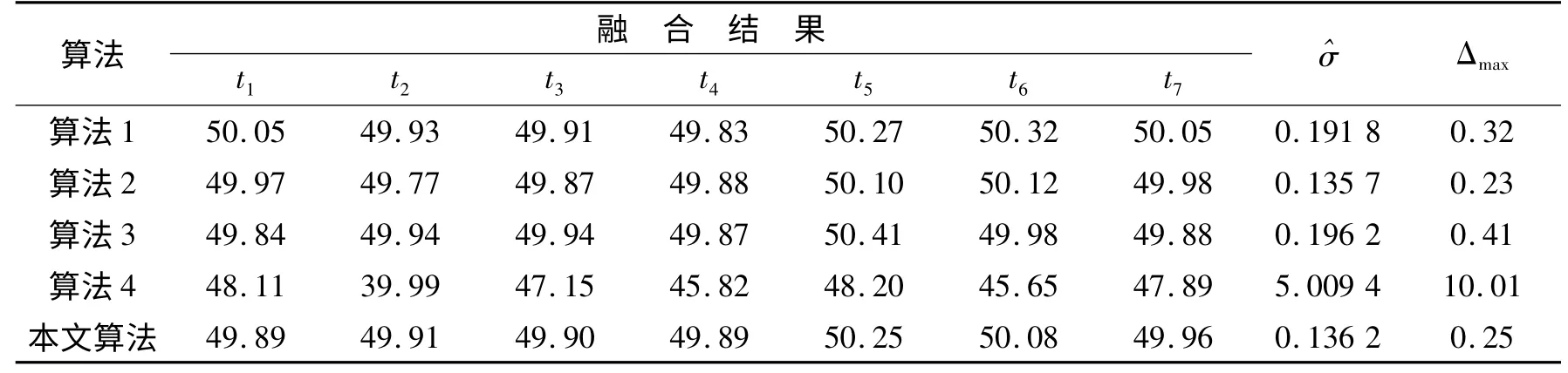
表3 不同融合算法融合值及融合效果评估(各传感器均正常)Table 3 Fusion result and fusion effect evaluation of different algorithms(each sensor is normal)
由表3 可以看出,除算法4 外其余算法对测量数据的融合效果均较好,这是由于表2 中的测量数据均在各传感器工作正常情况下给出。其中,算法2 的融合结果总体修正标准差与极限偏差值均优于其他算法,这是由于在测量数据与相应传感器初始精度对应性好的基础上,基于传感器初始精度的最小二乘加权融合算法生成的融合值均方误差最小。
为便于直观显示,将表3 中不同采样时刻对应的各算法融合结果作图。由于算法4 的融合误差过大,将其融合结果绘入图中意义不大,因此只对其余4 种算法作图,如图2 所示。
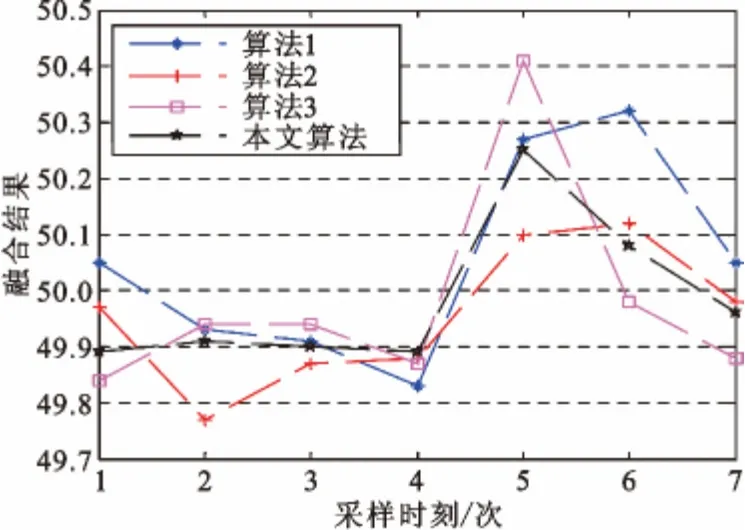
图2 不同融合算法在各采样时刻下测量数据融合结果Fig.2 Fusion results of different fusion algorithms at each sampling time
由图2 可以看出,同样基于传感器实测数据间相互距离生成数据融合时的权重值,本文算法与算法3 在融合结果上具有相同的趋势,并且本文算法更加收敛。由于在t5时刻,6个传感器中有4个传感器测量数据均偏大,因此本文算法与算法3 在此时刻的融合值也偏大。而精度最高的传感器1 在t5时刻测量数据稍偏小但准确度高,因此基于算法2生成的融合值准确度较高。传感器精度越高,越容易受到外界干扰,假若由于外界环境扰动或者传感器自身波动导致实际测量数据与传感器精度出现不匹配情况时,基于算法2 所生成融合值的融合效果将大打折扣。下面,通过算例2 予以验证。
算例2:假设精度最高的传感器1 由于受到干扰发生故障,导致测量数据出现大的波动,其余传感器测量数据不变。设传感器1 精度因故障变为1.2,测量数据如表4 所示。

表4 传感器1 故障情况下测量数据Table 4 Measurement data when sensor 1 is fault
同样采用算法1、算法2、算法3、算法4 以及本文算法对表2 (部分)与表4 中各传感器测量数据进行融合,各算法融合结果及融合效果评估如表5 所示。由表5 可以看出,算法4 的融合效果仍然非常差,因此文献[8]在将传感器初始精度生成的权重与实际测量数据生成的权重进行综合考虑时,所给出的综合方式是错误的(文献[8]的数据计算结果有误)。由于测量精度最高的传感器1 发生故障导致该传感器测量数据出现较大偏差,算法2 采用固定权重法,在融合时仍然赋予传感器1 测量数据最大权重,融合结果显然偏差较大。
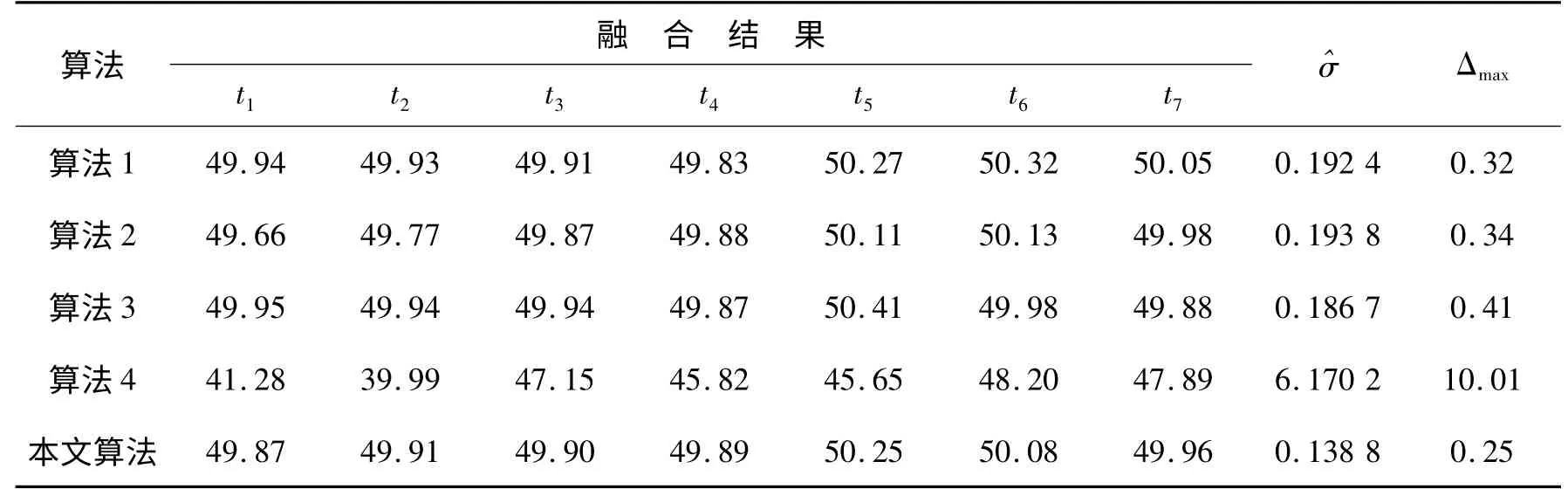
表5 不同融合算法融合值及融合效果评估(传感器1 故障,其余正常)Table 5 Fusion result and fusion effect evaluation of different algorithms(sensor 1 is fault and other are normal)
为便于直观对比分析,将两种情况下两次融合结果的总体标准偏差与极限偏差分别作图,如图3 所示。

图3 传感器1 正常与故障情况下融合效果对比Fig.3 Fusion effect comparison between normal and fault conditions of sensor 1
对图3 进行分析,可以得出:
(1)当传感器1 发生故障时,算法2 的融合效果相比于传感器1 正常时显著变差,其余算法变化不大;
(2)传感器1 正常时,算法2 融合效果在所有算法中最优;传感器1 故障时,算法2 融合效果与其他算法相比基本处于最差;
(3)算法1 与算法3 在传感器1 故障前后的融合效果变化幅度不大,但两种情况下该两种算法融合效果均较本文算法差;
(4)本文算法在传感器1 发生故障时,融合效果稍有降低,但两种情况下与其他算法相比均为最优。
3.2 传感器初始精度未知
当初始精度未知时,分为两种情况对算法进行验证,一是能够基于实际测量数据计算传感器测量精度,另一种是传感器测量精度无法通过计算获取。
3.2.1 传感器测量精度能够计算
以某系统贮罐温度传感器测量数据为例对本文算法进行验证,如算例3 和算例4 所示。
算例3:选定某系统贮罐状态稳定的一段时间,基于多个(本文选3个)温度传感器对贮罐温度进行监测,此时该监测过程可近似理解为静态测试过程。假设贮罐在监测时段内的温度理论值为25°,阈值范围为[24,26],超过阈值即报警。以3个服从均值为25、标准差分别为0.2、0.5、0.8 的正态分布随机变量模拟3个传感器的测量数据。限于篇幅限制,此处仅给出每个传感器的前10个模拟测量数据,如表6 所示。

表6 各温度传感器测量数据(部分)Table 6 Measurement data of each temperature sensor(part)
针对各传感器测量数据,分别随机选取20个测量数据计算各传感器测量精度,经计算后得出σ[c]=[0.198 1 0.450 8 0.605 1],显然与传感器实际仿真精度相一致。基于与本文所提融合算法对后续测量数据进行融合,选取20个测量数据进行融合,20 次融合结果的总体标准偏差值为0.238 4,极限偏差Δmax值为0.59。
3.2.2 传感器测量精度无法计算
当待测对象状态处于动态变化过程,此时无法依据历史测量数据计算传感器测量精度,则仅以测量权重作为相应测量数据的融合权值,完成多传感器数据融合。以某系统中泵的瞬时流量数据为例对本文算法进行验证,如算例4 所示。
算例4:选取某时段泵瞬时流量的10个流量值作为真值,如表7 所示。

表7 某泵瞬时流量真值Table 7 The true value of the instantaneous flow rate of a pump
以3个服从均值为0、标准差分别为0.5、0.8、1.2 的正态分布随机变量模拟3个流量传感器的测量噪声,用于干扰某泵瞬时流量真值。添加干扰后生成各流量传感器测量数据,如表8 所示。
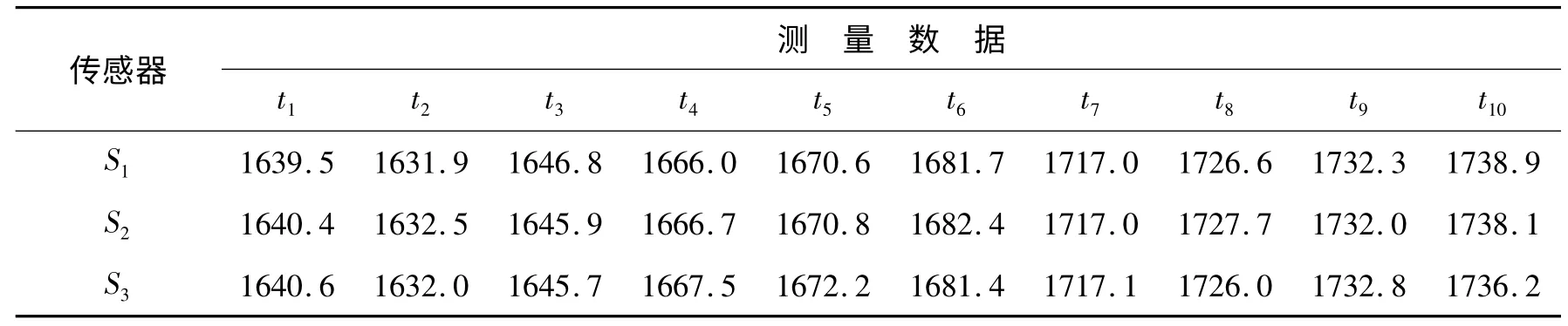
表8 各流量传感器测量数据Table 8 Measurement data of each flow sensor
基于本文算法对表8 中测量数据进行融合,融合结果如表9 所示。10 次融合结果的总体标准偏差值为0.495 0,极限偏差Δmax值为0.9。
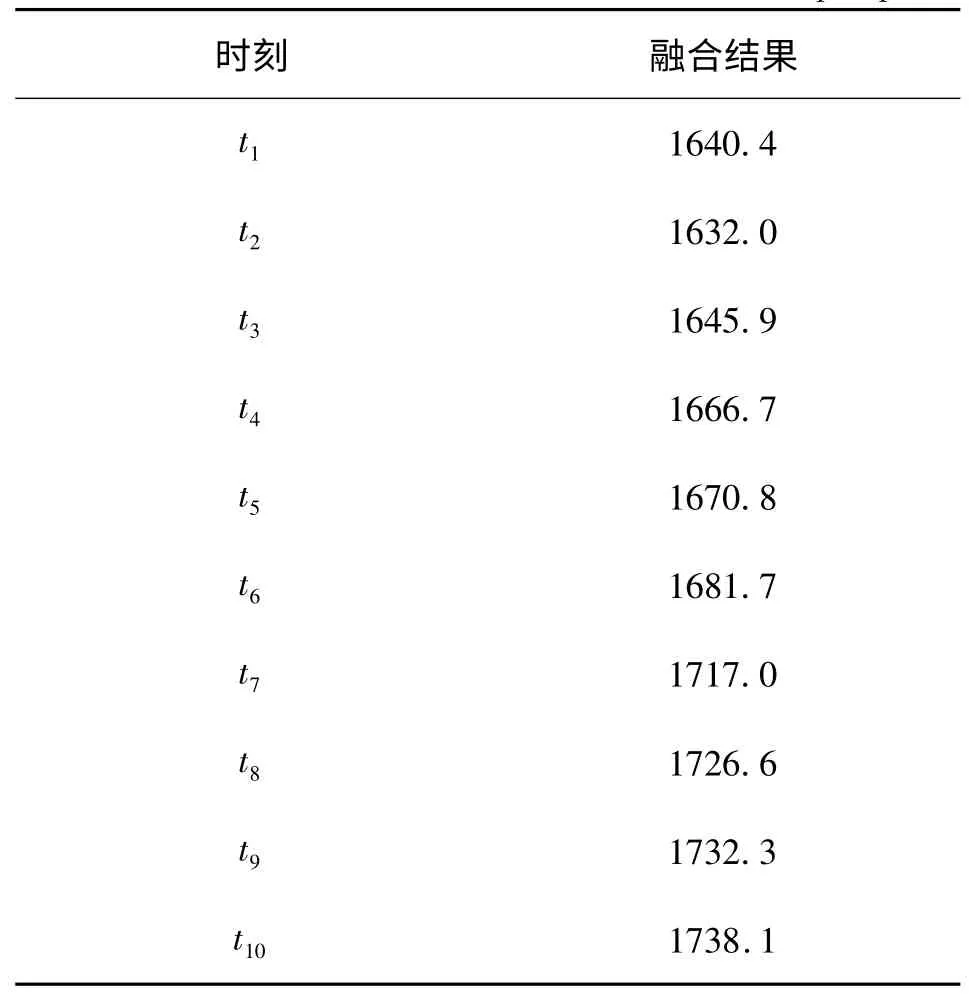
表9 某泵瞬时流量融合结果Table 9 The instantaneous flow fusion result of a pump
由融合结果可以看出,融合效果相比于算例1与算例2 稍差,这是因为本文仅根据20个测量数据生成了传感器测量精度,与实际精度值仍有一定误差。实际上,用于计算的传感器历史测量数据越多,得出的传感器测量精度越接近于实际精度。尽管融合误差有所增大,由极限偏差值可知融合结果仍均在许可范围内,故本文算法能够满足实际应用需求。
为便于对比分析,各时刻融合结果与待测真值对比如图4 所示。由表9 与图4 可得出,本文算法对处于动态变化的待测对象多传感器监测数据融合效果较好,满足实际需求。
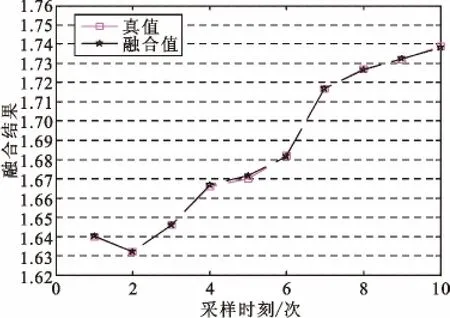
图4 各采样时刻融合值与真值对比Fig.4 The comparison of fusion value and true value at each sampling time
4 结束语
本文对当前多传感器数据融合中的加权融合算法进行研究与分析,在此基础上提出了一种综合考虑传感器初始精度与测量精度的改进自适应加权融合算法;将证据理论中的修正证据距离引入传感器测量数据间距离计算,并针对传感器初始精度已知(或能够计算得出)与未知两种情况,分别设计了相应融合模型。通过多个典型算例验证了本文算法的有效性与强鲁棒性。但本文仅考虑了同质传感器数据融合,针对异质传感器数据融合问题,仍需进一步深入研究。
[1]周尧,姜礼平,刘杨.复杂环境下基于支持度的多传感器数据融合算法[J].火力与指挥控制,2014,39(3):12-14,19.ZHOU Yao,JIANG Liping,LIU Yang.Data Fusion Algorithm Based on Support Degree under Interferential Environment[J].Fire Control & Command Control,2014,39(3):12-14,19.(in Chinese)
[2]宋文彬.差异维度传感器数据融合新方法[J].电讯技术,2013,53(3):254-258.SONG Wenbin.A New Data Fusion Algorithm for Sensor Measurements of Different Dimensions[J].Telecommunication Engineering,2013,53(3):254- 258.(in Chinese)
[3]张阳,沈明霞,孙玉文,等.基于多传感器自适应加权融合的温室信息系统[J].传感器与微系统,2014,33(6):100-103.ZHANG Yang,SHEN Mingxia,SUN Yuwen,et al.Greenhouse information system based on multi-sensor adaptive weighted fusion[J].Transducer and Microsystem Technologies,2014,33(6):100-103.(in Chinese)
[4]张军,扬子晨.多传感器数据采集系统的数据融合研究[J].传感器与微系统,2014,33(3):52-54,57.ZHANG Jun,YANG Zichen.Study on data fusion of multisensor data acquisition system[J].Transducer and Microsystem Technologies,2014,33(3):52-54,57.(in Chinese)
[5]焦竹青,熊伟丽,徐保国.基于加权最小二乘法的异质传感器数据融合[J].吉林大学学报(工学版),2010,40(3):816-820.JIAO Zhuqing,XIONG Weili,XU Baoguo,et al.Dissimilar sensor data fusion based on weighted least square[J].Journal of Jilin University(Engineering and Technology Edition),2010,40(3):816-820.(in Chinese)
[6]金建华,阙沛文.多传感器测量数据的切尾加权融合算法[J].仪器仪表学报,2002,23(增3):303-304.JIN Jianhua,QUE Peiwen.A trimmed mean- based weighted fusion algorithm of multi-sensor data[J].Chinese Journal of Scientific Instrument,2002,23(Suppl.3):303-304.(in Chinese)
[7]朱忠祥,韩科立,宋正河,等.基于置信度加权的拖拉机组合导航融合定位方法[J].农业机械学报,2013,44(增刊):210-215,223.ZHU Zhongxiang,HAN Keli,SONG Zhenghe,et al.Fusion Positioning Method Based on Weighted-confidence for Tractor Integrated Navigation[J].Transactions of the Chinese Society for Agricultural Machinery (Suppl.),2013,44:210-215,223.(in Chinese)
[8]熊彦铭,李世玲,李军,等.多传感器时间控制系统的数据融合新算法[J].弹箭与制导学报,2012,32(1):171-174.XIONG Yanming,LI Shiling,LI Jun,et al.Novel data fusion algorithm for multi- sensor delay- control system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(1):171-174.(in Chinese)
[9]李程,王伟,施龙飞,等.基于多源信息融合的有源雷达组网方式序贯识别方法[J].电子与信息学报,2014,36(10):2456-2463.LI Cheng,WANG Wei,SHI Longfei,et al.Sequential Method for Netting Type Recognition of Active Radars Based on Multi-source Information Fusion[J].Journal of Electronics & Information Technology,2014,36(10):2456-2463.(in Chinese)
[10]彭颖,胡增辉,沈怀荣.一种修正证据距离[J].电子与信息学报,2013,35(7):1624-1629.PENG Ying,HU Zenghui,SHEN Huairong.A modified distance of evidence[J].Journal of Electronics &Information Technology,2013,35(7):1624-1629.(in Chinese)

