基于Sollin算法的快速聚类研究

刘 欢

（渤海船舶职业学院，辽宁兴城125105）

0 引言

文本作为信息载体，因其数量巨大而难以甄别。文本聚类技术作为处理和组织大量文本数据的一项重要技术，能够在很大程度上解决由于信息爆炸所带来的问题。文本聚类是通过数据集的空间分布情况以及相似性度量方法对数据进行分析。根据聚类方式的不同，文本聚类可以分为划分式聚类和层次聚类。由于层次聚类算法简单容易实现且适合多种形状分布的数据，因此本文主要对层次聚类进行研究。

层次聚类按照聚类过程的不同可以分为自上而下的分裂式聚类方法和自下而上的凝聚式聚类方法。较经典的层次聚类算法有BIRCH算法和CURE算法。

传统的层次聚类算法因为合并方法单一且计算量巨大，造成聚类质量大大降低。因此本文提出了基于Sollin的快速层次聚类算法，使得运行效率和聚类质量都有明显的提升。

1 相关知识

1.1 层次聚类

层次聚类又称为树聚类算法，它根据数据之间的相似度，通过一种层次架构方式，反复的将数据进行分裂和聚合，从而形成一种树状的层次聚类解。本文主要研究自底向上的聚合方法，首先将每一个对象作为一个簇，然后每次合并相似度最大的两个簇，直到所有的数据对象都在一个簇中或者达到某个终结条件为止。传统层次聚类算法如图1所示。

图1 传统层次聚类过程

输入：n个样本点

输出：k个类

步骤：1）将每个数据对象看作一个簇，计算它们之间的相似度sim（i，j），簇之间的相似度就是它们所包含的对象之间的相似度；

2）将相似度最大的两个簇合并成为一个新的簇；

3）重新对新的簇与其他簇之间的相似度进行计算；

4） 重复步骤 （2） 和 （3），直到所有数据对象在一个簇中或者达到某个终结条件。

层次聚类在聚类的过程中需要对簇进行合并或分裂操作，因此除定义样本点之间的距离外，还要定义簇与簇之间的距离，常用的簇间距离表示方法有以下3种：

单链接，即使用两簇之间最相似的两个样本点之间的相似度作为两簇之间的相似度，如图2（a） 所示。

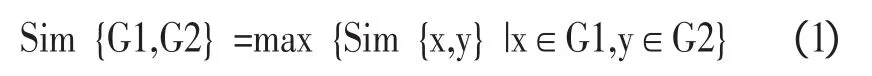
全链接，即使用两簇之间最不相似的两个样本点之间的相似度作为两簇之间的相似度，如图2（b） 所示。

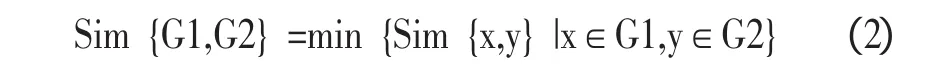
平均链接，即使用两簇之间所有样本点之间的相似度之和的平均值作为两簇之间的相似度，如图2（c） 所示。

图2 簇间相似性表示方法

在以上3种距离表示方法中，相对于单链接和全链接而言，平均链接介于两者之间，它充分考虑到了簇与簇之间每个样本点之间的距离，计算出来的簇间距离更接近实际情况，具有一定的优越性能。

1.2 Sollin算法

Sollin算法是构建最小生成树的典型算法，它是基于贪心策略的局部最优算法，与Kruskal算法和Prim算法相比，Sollin算法容易实现并行运算。

Sollin算法构建最小生成树的基本步骤是将连通图中所有顶点当作一棵树，原连通图就成为了一个森林；然后每棵树同时决定其连向其他树的最小权值临边（临边可以是同一条边），并与这个最相邻的节点结合成一棵树；最后重复上一步骤，直到所有节点都在一棵树上为止。图3为Sollin算法构建最小生成树的实例。

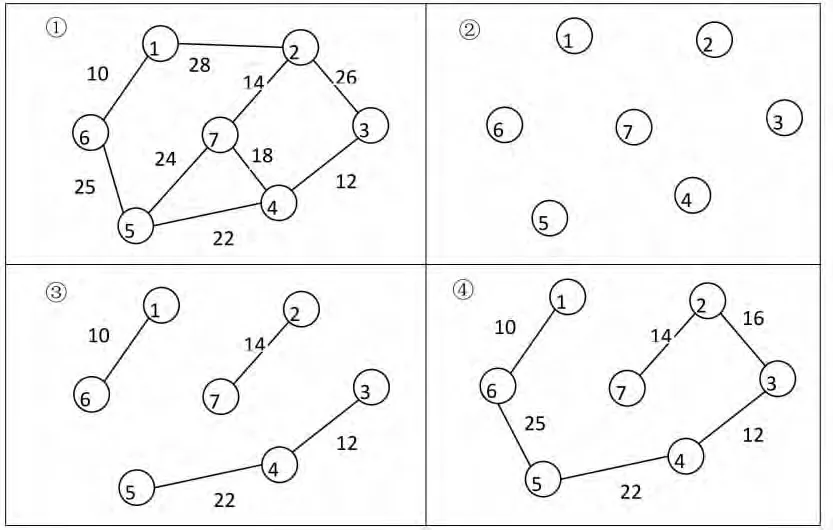
图3 Sollin算法构建最小生成树

2 基于Sollin的快速层次聚类算法

层次聚类算法实现简单，且聚类精度较高，但是其时间复杂度也较高，对于孤立点的处理能力非常弱。基于Sollin的快速层次聚类算法通过并行合并各子簇来降低聚类过程中的时间消耗，每层各个子簇都会找到与自己最相似的子簇进行合并，即可以消除孤立点单独成类的问题。基于Sollin的快速层次聚类算法的基本思想如下：

输入：n个数据对象

输出：k个类

步骤：1）设有n个数据对象，将每个数据对象当作一个簇；

2）计算各簇之间的相似度；

3） 通过Sollin构建最小生成树的算法将数据合并成m（m＜n）个最小生成树；

4） 重复步骤 （2） 和 （3） 的过程，直到m＜=k为止；

5） 如果m＜k，则将 （k-m） 条相似度最小的边断开，从而形成k个类。

Sollin算法是构建最小生成树的典型算法，因此基于Sollin的快速层次聚类算法在每层的聚合过程都可以看作是构建最小生成树的过程。这样既可以实现聚类算法的并行运算，提升其聚类效率；又可以消除孤立点单独成类问题，提升其聚类质量。

3 实验

3.1 实验数据

本实验选择复旦分类语料和搜狗分类语料（下载于“数据堂”） 作为实验数据，如表1和表2所示。

表1 复旦语料

表2 搜狗语料

3.2 实验预处理

所有实验语料均通过中科院分词工具“NLPIR汉语分词系统”进行分词，根据哈工大的停用词表去除停用词。然后用向量空间模型表示每篇文章，其中词的权重用tf-idf表示，计算公式如下：

N—文本集中总的文章个数；

用向量夹角余弦值来表示各个文章之间的相似度，第i篇文章和第j篇文章之间的相似度为:

3.3 评测方法

给定数据集的正确分类结果D={L1，L2，…Li，…Lm}，第i个类的数目记为Li=ni，聚类以后，得到一个聚类结果C={c1，F···，cj，···，cm}，其中第j个簇中数据对象的数目记为cj=nj。在聚类结果中，类Li中被划分到类Cj中的数据对象的数目记为Li∩Cj=Nij。

式中P（i，j）—Li中元素在Cj中的正确率；

R（i，j）—Cj中Li元素的召回率。

一个聚类结果C的评分是D中所有类别在C中所有簇的最大值F的和。

3.4 实验分析

第一，运行效率对比实验。从运行时间上进行对比，如表3所示，可以看出基于Sollin的快速层次聚类算法比传统的层次聚类算法的运行效率高。

表3 运行效率对比

第二，用基于Sollin的快速层次聚类算法分别在复旦语料和搜狗语料上做实验，分别用单链接、全链接和平均链接的方法来衡量各个簇之间的相似度。通过这3种方法的聚类结果分析得出用平均链接来衡量簇与簇之间的相似度最准确，如表4所示。平均链接考虑到了两簇中各个样本点之间的相似性，从而减弱了簇内噪声点的影响。

表4 基于Sollin的快速层次聚类

第三，用传统的层次聚类算法和基于Sollin的快速层次聚类算法分别在复旦语料和搜狗语料上做实验，用平均链接来衡量各个簇之间的相似度。通过对最终的两个聚类结果进行比较，证明基于Sollin的快速层次聚类算法的聚类质量比传统的层次聚类算法的聚类质量好，且基于Sollin的快速层次聚类算法处理噪声点和孤立点的能力比传统的层次聚类算法强，如图4和图5所示。

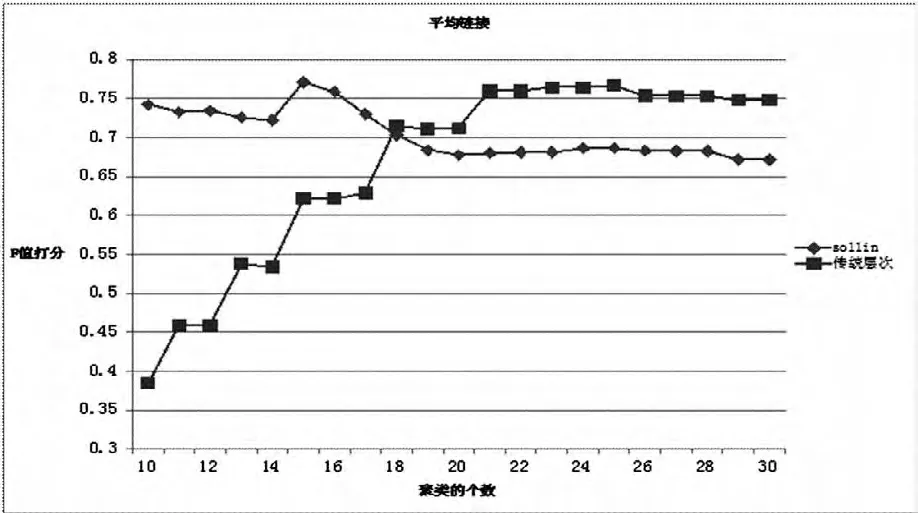
图4 复旦语料聚类结果

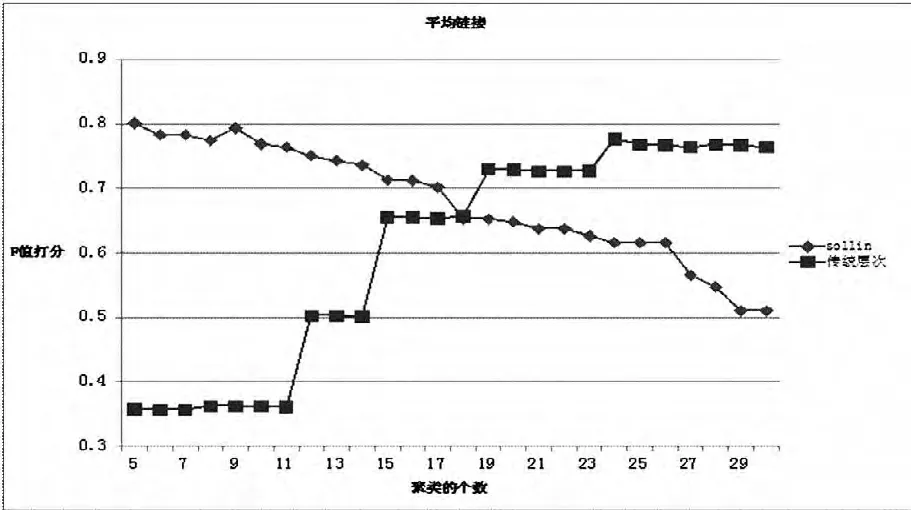
图5 搜狗语料聚类结果

由图4和图5可以看出，复旦语料的聚类个数在10～18类之间时，搜狗语料的聚类个数在5～18类之间时，基于Sollin的快速层次聚类算法的聚类质量要比传统的层次聚类算法的聚类质量高。而当聚类个数大于18类之后，传统的层次聚类算法的聚类质量高于Sollin算法的聚类质量。造成这种现象的主要原因是传统的层次聚类算法对噪声点和孤立点的处理力能较弱。

从基于Sollin的快速层次聚类算法的聚类结果中可以得出，复旦语料被聚为15类的时候F值最高（0.771），搜狗语料被聚为5类的时候F值最高（0.801），且F值随着聚类的个数增加呈下降的趋势。这表明随着聚类个数的增加同一类的样本集被分开，从而导致F值下降，进而证明基于Sollin的快速层次聚类算法具有较强的处理噪声点和孤立点的能力。

复旦语料包含10类文章，搜狗语料包含5类文章，从图4和5中可以看出在接近正确的聚类个数时，基于Sollin的快速层次聚类算法比传统的层次聚类算法的聚类质量要高很多。

利用基于Sollin的快速层次聚类算法，通过在复旦语料和搜狗语料上的聚类实验，证明了基于Sollin的快速层次聚类算法在运行效率和聚类质量上都优于传统层次聚类算法。但是基于Sollin的快速层次聚类算法也存在问题，如每层聚合过程中每个簇都会与自己最相近的簇进行合并，这样会造成提前聚类结束的簇与其他的簇继续聚合，会严重影响最终聚类结果。

[1]苏喻.基于语义的文本聚类搜索研究[D].合肥:安徽大学,2011.

[2]蒋盛益,李霞.一种改进的BIRCH聚类算法[J].计算机应用,2009(1):293-296.

[3]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008(1):48-61.

[4]陈海珠,郑卉.基于Sollin算法的最小生成树求解[J].计算机光盘软件与应用,2012(15):92-93.