静止自并励水轮发电机励磁扰动暂态仿真的实现

杨启军，罗 建，张 莉

（1. 重庆电力高等专科学校，重庆 400039；2. 重庆大学，重庆 400044）

大型同步发电机暂态仿真是电力系统开展动态和暂态稳定性分析、故障分析、参数辨识和仿真系统开发的重要前提。当遭遇突然加减负载、励磁电流扰动、内部或外部短路故障等异常运行时，发电机将处于暂态过程，其定转子各绕组的电压、电流、磁链及电磁转矩、功率、转速等物理量将随时间变化。在ABC三相系统下，由于同步发电机转子绕组的不对称，定子绕组与转子绕组之间的互感随时间的变化，因此实际分析同步电机时多采用Park变换。经过Park变换，可将发电机A、B、C定子绕组变换成在dq0坐标下的d轴、q轴等效绕组以及0轴绕组，发电机的电压方程和磁链方程将由非线性时变的微分方程变成线性常微分方程，这为发电机暂态仿真的研究提供了方便。

当前，许多文献均采用Matlab Simpowersystems中的同步发电机既有的dq0模型开展暂态仿真研究。但是，该模型的稳态输出与理论分析结果相比较有很大的误差，显然也不能用于同步发电机精确的暂态仿真。同时，许多文献在发电机暂态仿真研究中，大多认为稳态时发电机励磁电压为恒定值，但仿真结果并不完全符合实际。因为当前大型同步发电机大都采用静止自并励励磁方式，发电机励磁电压的波形即使在稳态下实际是锯齿波，而不是恒定的直流。

为了更深入地研究发电机暂态过程，本文寻求用数值法来精确求解发电机暂态过程中各电磁量的数值解，其方法是在时域上选择合适的状态变量，将发电机电压方程、磁链方程、运动方程转化为状态方程后编程序加以求解。本文先导出一组基于发电机电压方程、磁链方程、运动方程的状态方程，再对其离散化，然后采用四阶Runge-Kutta法编写迭代求解程序，最后对某静止自并励励磁方式的700 MW 水轮发电机励磁扰动的暂态过程进行仿真，验证了本仿真模型的正确性。

1 同步发电机派克方程及运动方程

同步发电机派克模型是基于电路参数，以电压、磁链、转速为状态变量的。

在该模型中，基于发电机惯例的暂态过程电压方程为

式中各量均为标幺值。其中：ud、id、ψd和为定子d绕组的电压、电流、磁链和磁链的导数；uq、 iq、和定子q绕组的电压、电流、磁链和磁链的导数；u0、i0、ψ0和为定子0绕组的电压、电流、磁链和磁链的导数；uf、if、ψf、 和 rf为励磁绕组的电压、电流、磁链、磁链导数和电阻；r为定子绕组的电阻； 为转子的电角速度；ψD、和iD为直轴阻尼绕组的磁链、磁链导数和电流；ψQ、和iQ为交轴轴阻尼绕组的磁链、磁链导数和电流。

磁链方程为

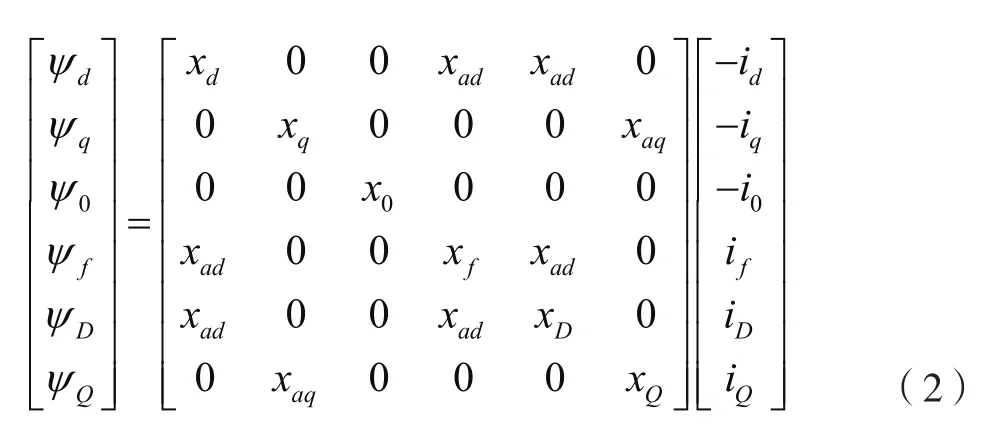
式中，xd、 xq、 、 xf、 xD和 xQ为各绕组的自电抗标幺值；ad为d、f、D三绕组间的互电抗标幺值；xaq为q、Q两绕组间的互电抗标幺值。

描述发电机动态过程的运动方程为

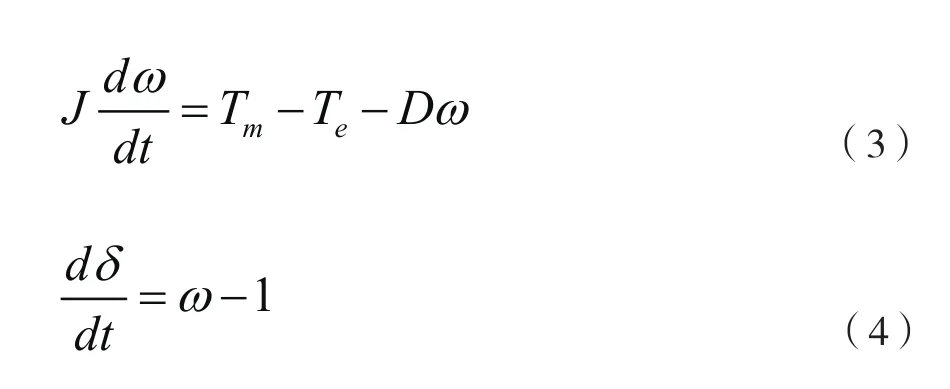
式中，J为转动惯量标幺值；mT为输入的机械转矩标幺值；eT为电磁转矩标幺值；D为阻尼系数；δ为功角有名值，单位rad。

上述式（1）～（4）构成了描述同步发电机暂态运行的基本方程。

2 同步发电机的状态方程和功率方程

上述暂态方程必须在时域上才能进行数值求解。为此，需将其转化为状态方程形式。

根据电机学知识可知，发电机端电压U、功角δ与d轴电压du和q轴电压 qu之间的关系为

发电机电磁转矩eT的计算方法为

假设发电机中性点不接地，暂不考虑0轴电压方程和磁链方程，将式（2）、（5）分别代入式（1）、（3）、（6），经整理后可将发电机基本方程转化为如下状态方程

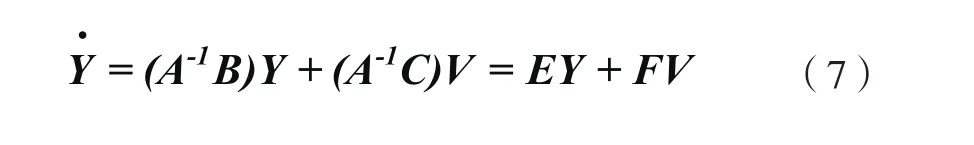
其中，E、F为系数矩阵，E =A-1B，F =A-1C。而矩阵A、B、C的计算方法为

状态向量Y为

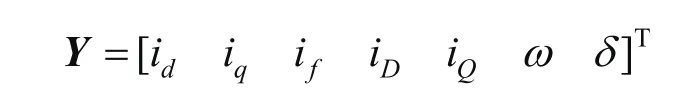
控制向量V为

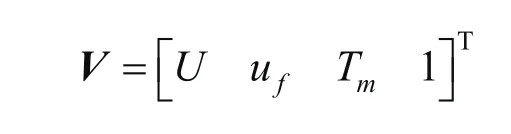
式中，fu为励磁电压各时刻的数值仿真值，呈余弦规律变化。

另外，发电机有功功率和无功功率可由下述两式求得

在励磁扰动的条件下，求解状态方程（7）可得到状态量Y的数值解；将数值解带入式（8）可求取发电机有功功率和无功功率的瞬时值。

3 状态方程的数值求解原理

由矩阵B、C的表达式可看出，矩阵B、C含有状态变量，使得状态方程具有非线性性质，必须用数值法来求解。本文采用电机工程上常用的四阶Runge-Kutta法求解。具体算法为：时间步长若为h，第i步状态变量Yi已知，则第i+1步的状态变量Yi+1计算方法为

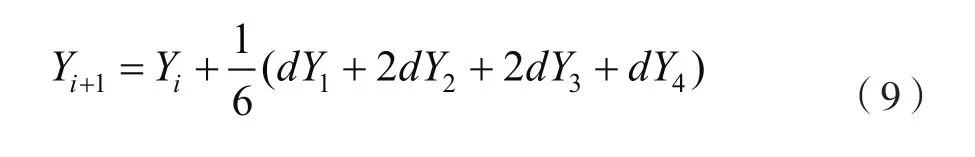
其中，d Y1、 d Y2、 d Y3和dY分别为时刻 ti，ti+0.5h，ti+ 0 .5h，ti+ h 时刻状态相量的增量，可用 ti-1时刻的状态量代入式（10）计算

值得指出的是，式（10）中的E、F、V是变化的，每一次计算时刻都要重新计算一次或带入新的向量。这样，一旦状态向量的初值给定，以此为起点一步一步向前计算即得整个暂态过程的状态向量。从而，暂态过程任意一时刻的各物理量可根据该时刻的状态向量来计算。

4 程序设计及仿真实例

本文仿真原型为某大型水轮发电机，其基本参数 为 ： Pr=700 MW，Ur=18 kV，fr=50 Hz，cosφ=0.9，If0=190.7 A，Uf0=1979.6 V，nr=107.1 rpm，GD2=220 000 t.m2。根据生产厂家给出的实用参数，可换算得到如下派克方程模型参数：r=0.001 531 2，rf=0.000 327 1，rD=0.009 358，rQ=0.006 814，xd=0.977，xq=0.703，xf=1.00，xD=1.059 9，xQ=0.667 88，xad=0.821，xaq=0.547，其中所有阻抗参数均为标幺值，转子基准值的选择符合xad准则。发电机励磁方式为静止自并励。

仿真系统为自并励励磁方式的单机无穷大系统。基于精确派克方程模型及运动方程的水轮发电机仿真模型，具体可用matlab语言编程实现，但不作任何假设，以提高仿真的精度和可信度。根据式（11），锯齿波励磁电压可采用数值模拟方法实现，但暂不考虑换相压降。根据文献，励磁状态下一个锯齿波励磁电压的瞬时值表达式为

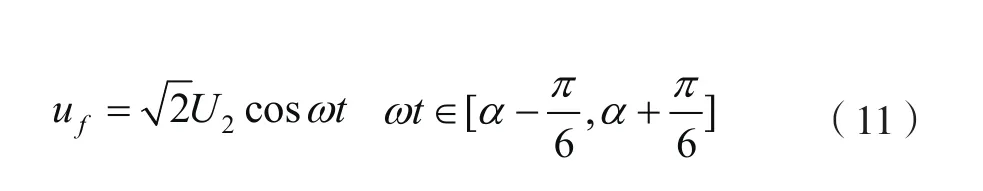
式中，fu为励磁电压；2U 为励磁变压器二次侧电压；α为脉冲触发角。

根据状态方程，按照图1程序框图编制matlab程序，即可求解基于励磁扰动的静止自并励水轮发电机暂态过程的时域解。

具体仿真时，将暂态仿真时间设定为48 s，换算成标幺值为15 079.6；仿真步长标幺值设为0.104 72时，发电机模型求解相对稳定，对应实际仿真步长时间为0.000 333 s；扰动前发电机处于稳定运行状态，在t=0s时励磁触发脉冲触发角由1.324 7rad （75.9°）扰动为1.371 2rad（78.56°），可获得扰动发生后暂态过程发电机出口电压和电流、励磁电压、励磁电流、转速、功率角、有功功率和无功功率等实测数据。

根据仿真实测数据绘制的原始模型仿真曲线如图2～图7所示。特别强调：图5中锯齿波励磁电压波形和图7中d轴D阻尼绕组电流波形看似为带状，实为锯齿波或脉动波形，这是由于数据采样点数很大所致；图7中，d轴D阻尼绕组的电流与q轴Q阻尼绕组的电流暂态过程总体趋势基本一致，但由于d轴方向锯齿波励磁电压的原因，D阻尼绕组的电流暂态过程呈现一定的脉动效应，而阻尼绕组Q的电流暂态过程不具有脉动特征，其波形为单线的（图中该电流隐藏在D阻尼绕组的带状波形中了）。

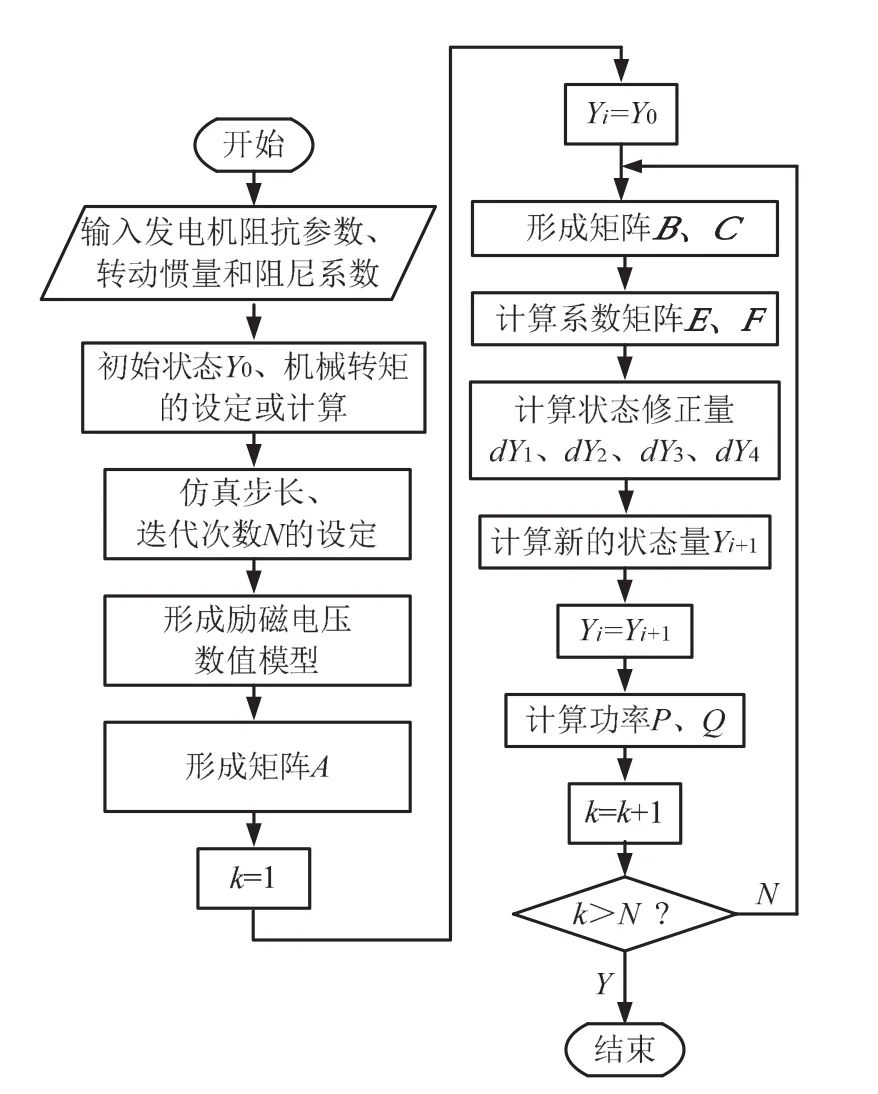
图1 同步发电机暂态过程求解程序框图

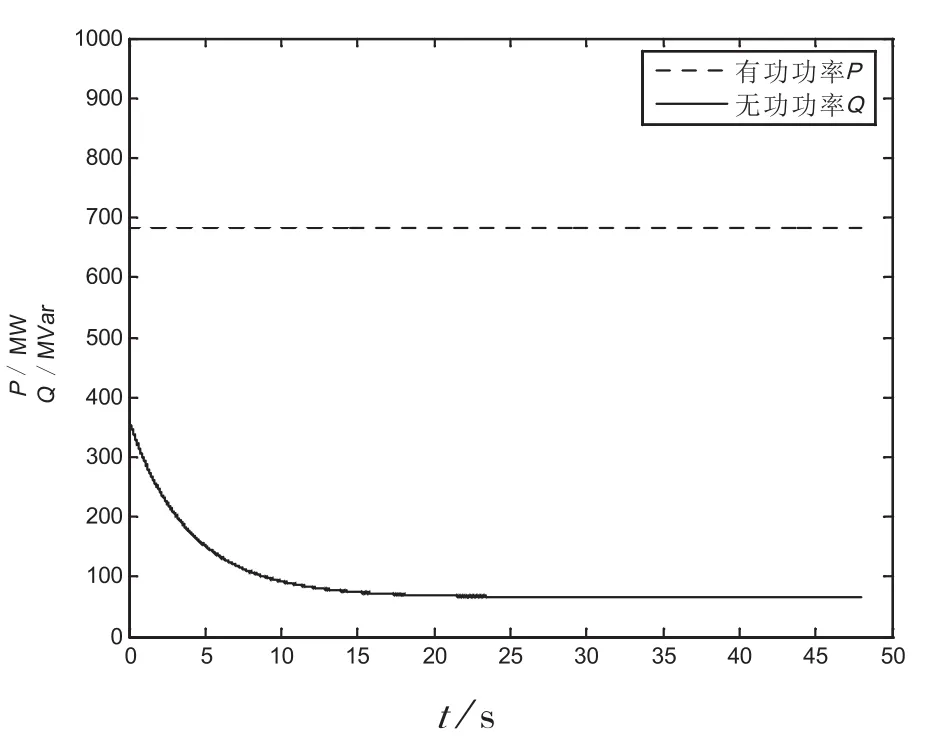
图2 发电机功率暂态曲线

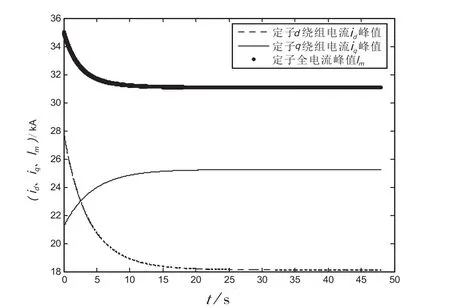
图3 发电机

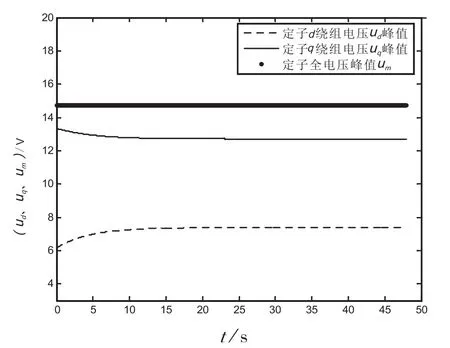
图4 发电机定子电压暂态曲线

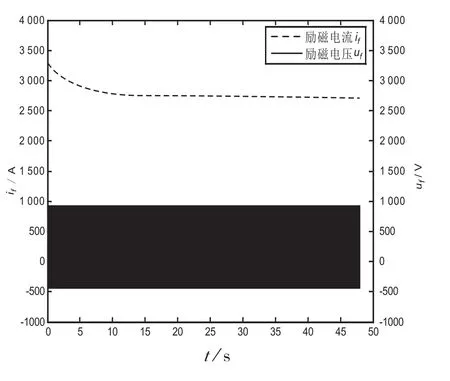
图5 发电机励磁电流和励磁电压暂态曲线

图6 发电机转速、功率角暂态曲线

图7 发电机阻尼绕组电流暂态曲线

5 结论

（1）由仿真结果可以看出，在暂态的最初时段（约1～5s）内，除转速、定子全电压和有功功率外，其余物理量发生较大的变化，特别是定子电流、励磁电流和阻尼绕组电流。随后各量逐渐稳定下来，稳定下来的时间大约需要20 s左右。

（2）虽然励磁电压波形是锯齿波，但是由于发电机励磁回路强大的电感使得励磁电流波形几乎没有脉动或锯齿波电流的特征，这一点和物理分析及实际测量波形是一致的。究其原因，是因为d轴D阻尼绕组的脉动效应平衡了同在d轴方向的f励磁绕组的励磁电压的锯齿波脉动效应。而q轴方向的Q阻尼绕组的电流由于不用平衡脉动效应，故其电流波形没有脉动特征。

（3）阻尼绕组在扰动发生后，有一个较高的电流冲击值，大约为230 A左右。稳定后，Q绕组稳定电流平均值几乎等于零，但D绕组脉动电流的平均值实际上不等于零，大概等于10 A左右。显然，认为D绕组是没有稳态电流的结论对于自并励发电机而言是不准确的，对发电机设计和发电机稳态运行分析时，应注意这个现象。

（4）本文仿真结果与用电机学理论计算的稳态结果完全一致，并且本文所建立的仿真模型，笔者已成功运用于某大型水轮发电机的参数辨识，其参数辨识结果精确度很高，说明本文提出的暂态分析模型是正确的、可信的。

［1］ 倪以信，陈寿松，张宝霖.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002.

［2］ 鞠平.电力系统非线性辨识［M］ .南京：河海大学出版社，1999.

［3］ 李基成.现代同步发电机励磁系统设计及应用［M］. 2版 .北京：中国电力出版社，2009.

［4］ 蒙泽森，何祖威，杨晨.基于时域的汽轮发电机暂态仿真［J］ .重庆大学学报 ：自然科学版，2006，（8）：53-56.

［5］ 王晶.电力系统的MATLAB/SIMULINK仿真与应用［M］ .西安：西安电子科技大学出版社，2008.