实时气象因子对空调负荷的影响及处理

赵晓丹

(西南交通大学，四川 成都610031)

随着人民收入与生活水平的提高、消费观念的变化，空调已得到大量普及，形成了不可忽视的空调负荷。据统计，除辽宁省以外，其他各省的电网空调负荷在电网负荷中所占比例均在30%以上，在我国一些经济发达的省份，尤其是在一些大中城市里，这个比例甚至已经达到或超过40%。例如，华东电网2010年夏季空调负荷约占电网高峰负荷的31%;江苏省2010年夏季空调负荷超过700万kW，约占最高电网负荷的32%;南京市夏季空调负荷超过120万kW，约占最高电网负荷的32%［1］。另外，用电负荷可以分为四个部分:基本负荷(与气象因子相关性很小)、气候敏感负荷(与气象因子相关性很强)、随机负荷、突发事件负荷［1］。文献［1］中对所有的负荷进行统一预测，并没有进行分类预测，而有的负荷对气象因子并不敏感，势必造成负荷预测的误差偏大。

空调负荷属于典型的气候敏感负荷，气象因子对其影响最为明显，并且由于热岛效应和积累效应［2-3］，其开停还与之前的气象因子有关系。文献［4］中以前一日的24 h温度进行空调负荷预测，文献［5］中将温度、湿度、太阳辐射作为空调负荷预测的输入变量，文献［6］中将温度、湿度作为输入量，这些研究均未将实时气象因子考虑进去。仅仅考虑这些日特征气象因素，显然无法得到更为准确的结果。本文将实时气象因子(温度、湿度)引入空调负荷预测模型中，提高了预测的准确性，大大地减小了预测误差。

1 温度、湿度与空调负荷的相关性

影响空调负荷的因素很多［7-9］，如温度、湿度、风速等，把所有影响因素都考虑进去显然是不科学的，也是不可能的。本文只把与空调负荷相关性最大的温度、湿度作为影响空调负荷的气象因子进行分析。分析中去除双休日、节假日的影响，数据选取南京市某年的空调运行负荷。

1.1 温度与空调负荷的相关性分析

为了使空调负荷与温度在同一坐标下进行比较，对空调负荷数据按式(1)进行比例变换。

式中，L'，Lt，Lmax分别为空调负荷百分比，第 t(t属于1～24)时段空调负荷，最大空调负荷。

根据南京市2009年统计数据得到空调负荷与温度的关系和温度与空调负荷散点图，如图1和图2所示。

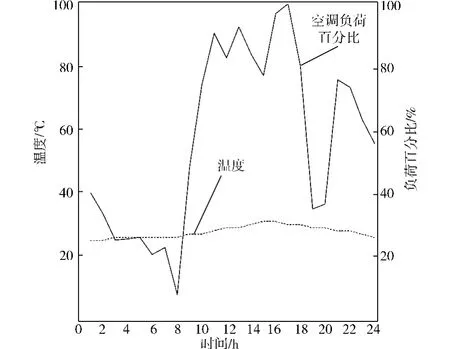
图1 空调负荷百分比与温度关系

图2 温度与空调负荷散点图

由图1和2可见，温度对空调负荷的影响很明显，相关系数为0.728 8，温度较高时空调负荷增加，温度较低时空调负荷下降。18点以后空调负荷下降，可能是因为工作人员下班所致，而20点以后空调负荷增加，主要是居民空调负荷上升。空调负荷的波动是因为分时电价，以及其他气象因子如风速等的影响。

1.2 湿度与空调负荷相关性分析

湿度与空调负荷关系图和湿度与空调负荷散点图如图3和图4所示。

图3 空调负荷百分比与湿度的关系

由图3和图4可见，湿度与空调负荷呈现出明显的负相关性，相关系数为0.625，即湿度较大时，空调负荷较低;湿度较高时，空调负荷较低。湿度与空调负荷的相关性不如温度与空调负荷的相关性明显。

2 空调负荷预测模型中考虑实时气象因子

目前，空调负荷预测中考虑的气象因子主要是日最高温度、日平均湿度、日天气类型等。但是，气象因子还具有实时性的特点［1，10］，即天气情况发生突变时，会对空调负荷造成相当程度的波动，简单地用日最高温度、日平均湿度、日天气类型等气象因子无法准确地预测出空调负荷。除此之外，气象因子的变化对空调负荷的影响是滞后的，在以15 min为间隔的96点负荷预测中尤为明显。由此可知，空调负荷预测模型将是一个多输入问题，处理多输入问题比较好的方法是BP神经网络。

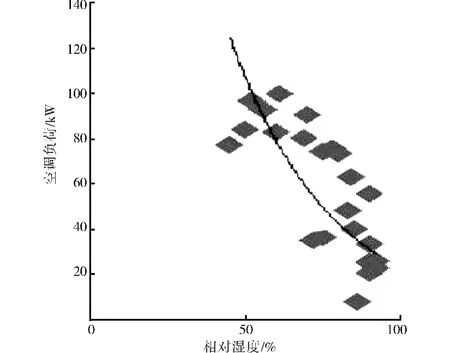
图4 湿度与空调负荷散点图

2.1 BP神经网络

BP神经网络，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐藏层(hide layer)和输出层(output layer)。隐藏层中的神经元均采用sigmoid型传递函数;输出层的神经元采用线性传递函数。BP神经网络结构如图5所示。

图5 BP神经网络

2.2 L-M算法

L-M算法是高斯-牛顿算法的改进，既有高斯-牛顿算法的局部特性又有梯度法的全局特性。由于利用了近似的2阶导数信息，L-M算法比梯度下降法速度快很多。

设误差指标函数为:

式中，ti，oi为期望输出与实际输出的误差，E(W)表示误差指标函数。

设W(k)表示第k次迭代的网络权值向量，维数为M新的权值向量，W(k+1)可根据下面的规则求得:

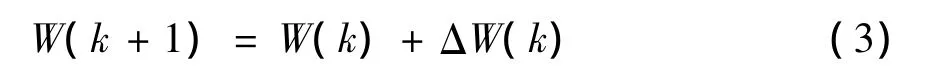
L-M算法是改进的高斯-牛顿算法，形式为:

式中，比例系数μ＞0;I是单位矩阵;J为雅可比矩阵。

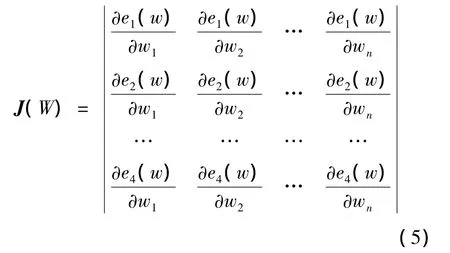
在实际操作过程中μ是一个试探性的数。对于给定的μ，如果求得的ΔW能使误差指标函数E(W)降低，则μ降低;反之，则μ增加。

2.3 神经网络设计

本文用一日96点计算，用神经网络形成96点空调负荷预测模型。此外需要对一天的气象因子进行插值处理，形成96点数据。合理的神经网络结构，既不能过于庞大，又要尽量包含所有的影响空调负荷的气象因子。本文使用三层网络结构，即一个隐含层。输出为预测日的空调负荷。输入层对准确预测很关键，本文输入层由17个输入神经元构成:

(1)当日的星期类型;

(2)当前时段;

(3)当日当前时段的前1时段的负荷;

(4)当日当前时段的前1小时(4时段)的负荷;

(5)当日当前时段的温度;

(6)当日当前时段的前1时段的温度;

(7)当日当前时段的前1小时(4时段)的温度;

(8)当日当前时段的湿度;

(9)当日当前时段的前1时段的湿度;

(10)当日当前时段的前1小时(4时段)的湿度;

(11)上周同类型日的当前时段的负荷;

(12)上周同类型日的当前时段的前1时段的负荷;

(13)上周同类型日的当前时段的前1小时(4时段)的负荷;

(14)上周同类型日的当前时段的温度;

(15)上周同类型日的当前时段的前1时段的温度;

(16)上周同类型日的当前时段的湿度;

(17)上周同类型日的当前时段的前1时段的湿度。

该输入变量的选取，考虑到了气象因子滞后效应，同时保留了同类型日预测的思想。

3 算例分析

本文数据选用南京市1999年空调负荷数据进行训练与预测。图6显示了空调负荷预测结果。

曲线表示，可以看出:

(1)考虑实时气象因子的空调负荷预测结果与实际负荷相差很小，最大误差在2%以内;

(2)预测结果与实际结果之间的误差可能是空调负荷的计算误差和样本训练误差引起的。

图6 预测空调负荷与实际空调负荷对比

3.1 预测模型比较

为了验证该模型的有效性，将不同的几种空调负荷预测模型进行误差比较。误差定义如下:

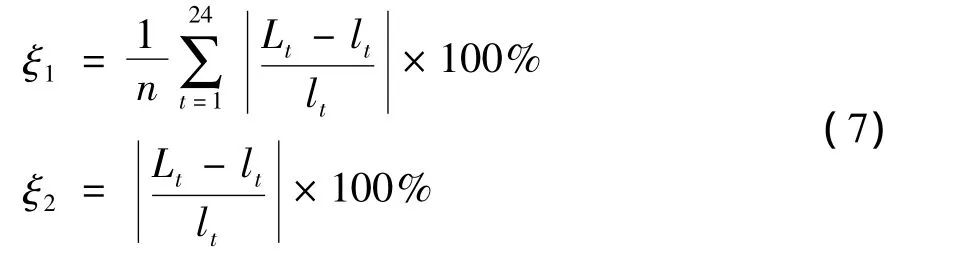
式中，ξ1和ξ2分别为平均绝对百分误差和绝对百分误差，Lt和lt分别为第t时刻的空调负荷预测值和实际值。

该模型与考虑日最高温度、日平均湿度模型［13］进行比较，结果如表1所示。

表1 误差比较

从表1可以看出，该模型，即考虑实时气象因子模型的平均绝对误差和绝对误差，均远小于考虑日最高温度、日平均湿度模型。

4 结束语

通过对气象因子温度、湿度对空调负荷影响的剖析，提出了考虑实时气象因子的空调负荷预测模型，并进行算例分析，验证了该模型的有效性。

空调负荷预测模型中的气象数据与空调负荷数据的获取，直接关系着预测模型的准确性。

［1］ 康重庆，周安石，王鹏，等.短期负荷预测中实时气象因素的影响分析及其处理策略［J］.电网技术，2006，(7):5-10.

［2］ 邱新法，顾丽华，曾燕.南京市城市干岛和湿岛效应研究［J］.气候与环境研究，2008，(6):808-809.

［3］ 黎灿兵.气温影响空调负荷的累积效应导致能耗的分析［J］.电力系统自动化，2010，(20):30-33.

［4］ 徐今强，肖睿，黄冲，等.空调负荷预测模型及仿真研究［J］.华中科技大学学报:自然科学版，2009，(Supp1):259-260.

［5］ 唐莉，唐中华，靳俊杰.最小二乘支持向量机(LSSVM)在短期空调负荷预测中的应用［J］.建筑节能，2013，(2):56-58.

［6］ 糜作维.空调负荷的预测与建模［D］.南京:河海大学，2005.

［7］ 陆建宇，王亮，王强，等.华东电网气象负荷特性分析［J］.华东电力，2006，(11):38-42.

［8］ 王治华，李扬，赵翠宇，等.南京市夏季气温敏感负荷研究［J］.电力系统自动化，2002，(3):60-63.

［9］ 张志强.基于电网侧的空调负荷特性分析及其调控措施研究［D］.北京:华北电力大学(北京)，2007.

［10］ Karaki.Weather sensitive short-term load forecasting using artificial neural network and time series［J］.International Journal of Power and Energy Systems，1999，(3):251-256.

［11］ 杜小瑾.中央空调轮停技术在夏季缺电形式下的应用［D］. 南京:东南大学，2006.

［12］ 朱晓清.电力负荷的分类及应用［D］.广州:华南理工大学，2012.

［13］ 刘旭，罗滇生，姚建刚，等.基于负荷分解和实时气象因素的短期负荷预测［J］.电网技术，2009，(12):94-100.