青藏高原积雪深度时空分布与地形的关系

白淑英，吴 奇，史建桥，顾海敏

(1.南京信息工程大学遥感学院，南京 210044;2.环境保护部南京环境科学研究所，南京 210042;3.94783部队61分队，长兴 313111;4.涪陵区气象局，涪陵 408000)

0 引言

越来越多的证据表明全球气候正在变暖，积雪变化必然对气候变化特别是区域气候产生重要影响。青藏高原作为北半球中纬度海拔最高、积雪覆盖最大的地区，其积雪时间长、空间分布广［1］，是北半球积雪异常变化最强烈的区域。积雪变化会对青藏高原靠积雪融化补给的河流和湖泊产生不容忽视的影响。卫星遥感技术具有快速、高效及便捷等优点，为积雪实时动态监测提供了有效的观测手段［2－3］，特别是在地面站点分布稀疏，甚至无站点的高原和山区，可以弥补地面站观测数据缺乏等不足。被动微波积雪数据［3－5］是全天候地表积雪的观测信息，不但能够用于区分地表有积雪与无积雪区域，还可以用于反演积雪深度或积雪水当量，基本不受云的干扰。经过很多学者的不断改进［6－8］，被动微波雪深反演数据的精度有所提高，已经能够较好地反映高原积雪的时空变化特征。

以往对高原积雪的影响因素研究主要从气候变化角度展开［9－11］，如降水和气温等，但气候因子对积雪变化的影响是作用在地形因子影响的基础上，随着海拔升高，气温逐渐降低，积雪融化变缓，从而影响雪深和雪盖的分布。青藏高原冰雪覆盖区是我国和南亚许多大江大河的发源地。气候变暖导致的降水重新分配、冰川加速消融、积雪提前融化、土地荒漠化和草场退化［12］等都会对积雪地区水资源数量与河川径流量季节分配的变化，以及周边与下游地区的气候变化产生重要影响。因此，本文以青藏高原为研究区，利用1979—2010年逐日中国雪深长时间序列数据集，采用GIS空间分析和Mann－Kendall检验，对雪深随高程、坡度的趋势和突变进行分析，揭示雪深对地形因子的响应，为进一步开展积雪时空变化规律、驱动因子及融雪径流模拟等研究提供参考信息。

1 数据与方法

1.1 数据来源与处理

积雪数据来源于中国西部环境与生态科学数据中心的“中国雪深长时间序列数据集(1978—2010)”。该数据集是由 SMMR(1978—1987年)、SSM/I(1987—2008年)及 AMSR－E(2002—2010年)3种被动微波遥感数据经交叉订正一致后，根据地面观测站实测雪深数据反演得到的逐日雪深资料，空间分辨率25 km，覆盖范围 E60°～140°，N15°～55°，采用全球等积圆柱EASE－GRID投影。首先，利用ArcGIS软件将1979—2010年逐日雪深数据转化为栅格数据;然后，根据栅格统计求得逐年逐月雪深(算术平均)和逐年逐月最大雪深数据(最大合成法);最后，在此基础上得到月平均雪深、年平均雪深(对月雪深求算术平均)、月最大雪深及年最大雪深数据(对月最大雪深进行最大合成)。

DEM是由 CGIAR ICT－ ICT(http://srtm.csi.cgiar.org)发布的SRTM3数据，分辨率为90 m，利用ArcGIS软件对DEM进行拼接、裁切及投影处理，得到青藏高原DEM数据，并对其进行坡度提取，结果见图1。

图1 青藏高原高程(左)和坡度(右)空间分布Fig.1 Spatial distribution of elevation(left)and slope(right)in the Tibetan Plateau

1.2 研究方法

1.2.1 Mann－Kendall检验

Mann－Kendall检验［13］不需要样本遵从一定的分布，不受少数异常值的干扰，计算较方便，常用于类型变量和顺序变量的趋势检验和突变分析［14－16］。

在Mann－Kendall趋势检验中，原假设H0为时间序列数据(x1，x2，…，xn)，其为n个独立的、随机变量同分布的样本;备选假设H1是双边检验，xk和xj的分布是不相同的，其中样本序列k≤n，j≤n，且k≠j，检验的统计变量S计算公式为

式中Sgn()为符号函数，即

确定方差Var和标准正态系统变量U，公式分别为

式中:如果U＞0，表明序列有上升或增加的趋势;如果U＜0，则表明序列有下降或减少的趋势。在给定显著性水平 α 下，当|U|＞U1－α/2时，表示序列趋势变化显著。当确定有显著趋势时，可以用线性方程或多项式方程模拟趋势方程。|U|≥1.28，1.96，2.32时，分别表示通过了信度90%，95%，99%的显著性检验。

在Mann－Kendall突变分析中，设时间序列x1，x2，…，xn;构造秩序列ri，其表示xi＞xj(i≥j≥1)的样本累积数。定义St为

其中t=2，3，…，n，

St均值E(St)以及方差Var(St)定义为

在时间序列随机独立的假定下，定义统计量为

式中:UF1=0;UFt为标准正态分布的统计量(t=1，2，…，n)，给定一显著水平 α，查正态分布表得到临界值Uα。当|UFt|＞Uα，表明序列存在显著增长或减少趋势，通过信度检验可知其是否具有显著趋势。按时间序列x逆序，再重复上述计算过程，得到逆序的标准正态分布的统计量UBt，同时使

然后绘出UFt和UBt曲线图。若UFt＞0，表明序列呈上升趋势，若UFt＜0表明呈下降趋势;当超过信度线时，表示存在显著的上升或下降趋势;若2条曲线出现交点，且位于信度线之间，那么交点对应的时刻就是突变开始的时刻。

本文分别利用雪深均值及标准差作为表征积雪的总体情况和空间异质性的变量，运用Mann－Kendall趋势检验进行雪深随高程和坡度的趋势分析，利用Mann－Kendall突变检验进行雪深对高程和坡度响应的突变分析。

1.2.2 多元回归分析

设雪深因变量为Y，n个自变量(气温、降水量、风速、日照时数、高程及坡度等)分别为X1，X2，…，Xn，则多元线性回归模型的一般形式为

式中:ε为随机误差;β0为回归常数;βj为总体回归系数，j=1，2，…，n。

实际中需要用样本信息对因变量进行估计。假设已给出n(样本容量)个雪深值，则多元回归线性模型的样本回归模型为

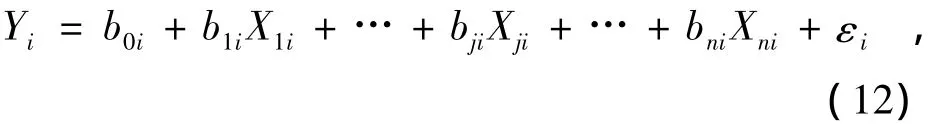
样本回归方程为

式中:为Xi第i值时对Y的估计值;b0i，b1i，b2i，…，bji，…，bni为总体回归参数的估计;εi为Yi与估计值的残差。b0，b1，b2，…，bn一定程度反映了自变量X1，X2，…，Xn对Y的解释程度，但解释程度是否显著还需T检验。在给定的显著水平下，自变量Xj对应的T值越大，则说明Xj对因变量Y的解释能力越强。本文拟将高程和坡度作为雪深的因变量，对雪深进行多元线性回归分析。

2 结果与分析

2.1 雪深空间分布

青藏高原1979—2010年间的年平均雪深分布如图2所示。

图2 1979—2010年青藏高原年平均雪深分布Fig.2 Spatial distribution of annualmean snow dep th in the Tibetan Plateau during 1979 to 2010

从图2可以看出，青藏高原积雪分布受气候和地形的影响显著，雪深分布的空间地域性和差异性明显，主要特征是中间小、四周大，多年平均雪深为2.03 cm，积雪深度1～3 cm所占百分比为54.8%，5 cm以上仅占5.3%。其中川西藏东山地、阿里山地半荒漠和荒漠地带积雪深度分布密集且较厚，雪深平均厚度在3 cm以上，而中部积雪疏散且雪深相对较浅，平均在0～3 cm之间。受高原地形阻挡作用，空中西风带冷槽分支沿高原西侧南下，高原西部处于西风带上升区，降水较多［17］;高原南部受印度洋和孟加拉湾暖湿气流影响，降水充沛;中部广阔的高原腹地由于受周围高山的地形影响，加之海拔较高，季风影响减弱，水汽输送较少，形成雪深低值区。

2.2 雪深与地形因子的响应关系

2.2.1 月最大雪深、月平均雪深与高程之间的关系

图3 青藏高原月尺度的雪深(月平均雪深、月最大雪深)与高程关系Fig.3 Relationships between monthly snow depth(monthly mean snow depth and monthly maximum snow depth)and elevation in the Tibetan Plateau

按月将雪深数据与对应高程进行空间分析，发现月最大雪深随海拔分布呈类似“凸”字型分布特征，并伴随有明显的陡坎效应，而这种陡坎效应在不同月份又有所差异。图3为青藏高原12个月份的雪深(月平均雪深、月最大雪深)与高程的关系图。可以看出，1，2，3，11，12 月份最大雪深的分布规律基本相似，最大雪深随海拔升高逐渐增加。在高程82～482m，最大雪深增幅速率达到5 cm/400 m，命名为“第一陡坡”;在高程482～2 082 m，最大雪深上升较为缓慢，增幅速率在1.6 cm/400 m左右，命名为“第二陡坡”;随后出现差异，1，11，12月的最大雪深随高程(2 482～3 282 m)变化表现为先平稳增加，在3 282 m附近存在陡坎，最大雪深突然大幅增长，3 682 m之后达到稳定状态。而2月与3月在2 482 m附近出现陡坎，最大雪深突然增加达6～7 cm，随后马上达到稳定状态。二者在5 682 m和6 882 m附近再次出现2个陡坎，最大雪深大幅减小;4，5，6月分布规律相近，“第一陡坡”和“第二陡坡”增幅速率大幅减小。5月与6月482 m以下基本没有雪，在高程2 482 m陡坎向高位推移变化到2 882 m(6月)，5 682m处陡坎消失，6月份6 882m处陡坎消失，最大雪深峰值也大幅减小。7月与8月“第一陡坡”和“第二陡坡”消失，高程2 082 m以下基本没有雪，在高程2 082～3 682 m和3 682～4 882 m雪深呈增加态势，在高程4 882 m附近存在陡坎，高程5 682 m以上雪深又逐步减小。9月高程2 082 m以下雪深稍有增加，最大雪深小于1 cm，在4 082 m最大雪深达到最大值4.2 cm左右，为年内最小值。10月份“第一陡坡”和“第二陡坡”重新建立，在高程3 282～5 682 m雪深变化平缓，高程5 682 m以上雪深呈缓慢下降趋势。另外，年内各个月份在高程7 682 m处均有陡坎，在此高程以上雪深突然大幅减小，但雪深基本保持不变。

从月平均雪深分布来看(图3)，1—5月雪深随高程呈“三峰”型分布，峰值高度在2 682 m，4 282 m和6 282 m附近，随着温度升高各高程带内的平均雪深逐渐减少，各峰值也在逐渐减小，但4 882 m以上平均雪深变化幅度较少;从5—9月，第一峰值和第二峰值逐渐消失，在高程4 882 m以下基本没有雪，平均雪深基本不受温度影响;随着温度下降，10—12月雪深“三峰”型分布重建，随高程升高月平均雪深逐渐增加。这说明平均雪深在5—9月主要受到高程的影响，在其他月份则主要受气温和高程共同的影响。

2.2.2 年最大雪深、年平均雪深与高程之间的关系

为研究青藏高原积雪信息对不同高程带的响应机制，对研究区高程进行400 m等密度分割。以年最大雪深的均值和标准差为参数分别与高程进行相关分析(图4)，相关系数分别为0.438和－0.609，均达到了0.05显著性水平，说明年最大雪深的均值分布随高程上升而增加，而年最大雪深的空间异质性则随高程逐渐减小。

图4 青藏高原年尺度的雪深与高程的关系Fig.4 Relationships between annual snow depth and elevation in the Tibetan Plateau

从图4可以看出，年平均雪深和年最大雪深均值随高程的变化趋势十分明显，二者变化趋势比较一致，相关系数达0.875，表现为明显分段特征，在高程82～2 482 m和2 882～4 482 m雪深逐步增加，但在高程2 482～2 882 m存在趋势转折，即峰值向谷值的急剧反转，之后雪深随高程上升而增加，在高程4 082～4 482 m年最大雪深的均值达到峰值10 cm;在高程4 482 m以上年最大雪深均值又转为波动减少趋势，在高程8 482 m以上雪深维持不变。年最大雪深的空间异质性随着高程上升也逐步增大，但在高程4 482 m以上年最大雪深空间差异性逐步减小。

Mann－Kendall趋势检验结果表明，青藏高原年最大雪深均值高程序列U1=1.551(1.28＜U1＜1.96)，年最大雪深标准差高程序列U2=－3.074(U2＜－2.32)，说明年最大雪深随高程的增加呈不显著上升趋势，年最大雪深的空间差异性随高程增加而呈显著下降趋势。在95%的置信水平下，Ua/2=1.96，利用Mann－Kendall法对年最大雪深高程序列的计算结果见图5。

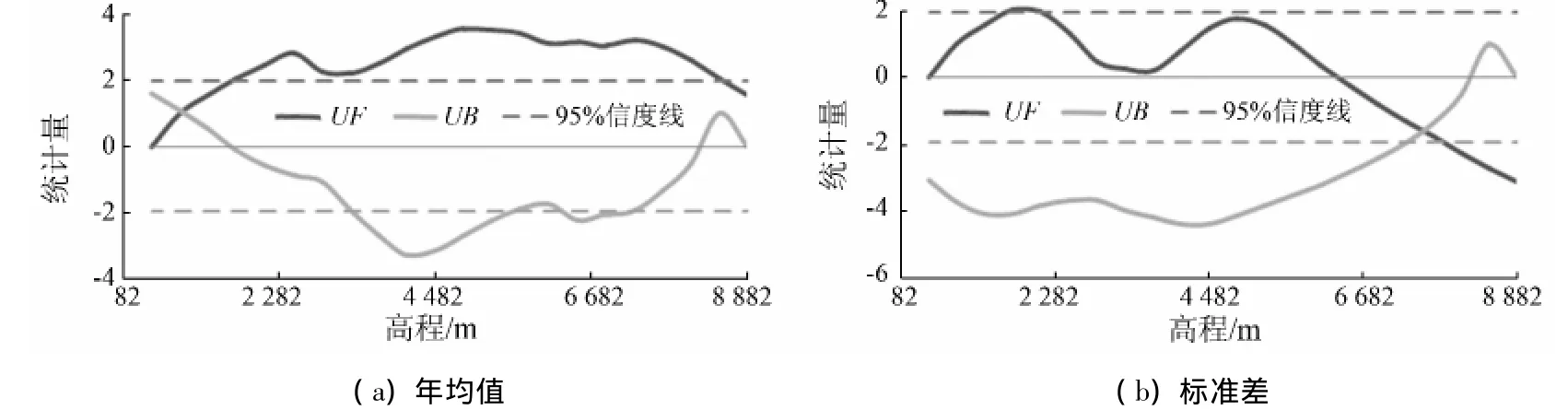
图5 年最大雪深随高程的M ann－Kendall法突变分析结果Fig.5 Annualmaximum snow depth with elevation mutation analysis results by M ann－Kendall

从图5可以看出，年最大雪深的均值随高程上升呈增加趋势，其中在高程小于1 682 m区域均呈不显著增加趋势，在高程1 682 m以上区域呈显著增加趋势，其随高程的突变点出现在882 m处;年最大雪深的空间差异性在高程6 082 m以下区域呈不显著增加趋势，在高程6 082 m以上区域呈减少趋势，高程7 682 m以上减少显著，空间差异性随高程的突变点出现在7 282 m处，说明高程7 282 m以下区域年最大雪深空间差异性大，相对而言，高程7 282 m以上区域年最大雪深空间差异较小。

2.2.3 雪深与坡度之间的关系

分析青藏高原积雪信息与坡度的响应机制时，对研究区坡度进行5°等密度分割。图6为青藏高原雪深与坡度的关系图。

图6 青藏高原雪深与坡度的关系Fig.6 Relationships between snow depth and slope in the Tibetan Plateau

从图6可以看出，年平均雪深在各坡度带均有分布，而且雪深随坡度的变化趋势比较明显，年平均雪深和年最大雪深的分布特征较一致，相关系数达0.926，均表现为单峰型特征，即雪深随坡度先增加后减少，峰值出现在40°～45°坡度带，年最大雪深平均值为12.5 cm。坡度在50°以下，雪深的空间异质性随着坡度增加也逐步增大，其中在20°～40°坡度带年最大雪深标准差变化不大，在45°～50°坡度带雪深的空间异质性最大，年最大雪深标准差达6.0 cm，随后雪深的空间异质性迅速减小，坡度在60°以上，雪深不存在空间差异。Mann－Kendall趋势检验结果表明，青藏高原最大雪深均值坡度序列U3=1.403(1.28 ＜U3＜1.96)，年最大雪深标准差坡度序列U4=2.013(1.96 ＜U4＜2.32)，说明年最大雪深随坡度的增加呈不显著上升趋势，年最大雪深的空间差异性随坡度增加而呈显著上升趋势。在95%的置信水平下，Ua/2=1.96，利用 Mann－Kendall法对年最大雪深坡度序列的计算结果见图7。

图7 年最大雪深随坡度的M ann－Kendall法突变分析结果Fig.7 Annualmaximum snow depth with slopemutation analysis results by Mann－Kendall

从图7可以看出，年最大雪深及其空间差异性随坡度的上升均表现为增加趋势，其中坡度在20°以下区域二者呈不显著增加趋势，在坡度20°以上则呈显著增加趋势，不同的是年最大雪深随坡度的突变点出现在坡度10°，年最大雪深的空间差异性的突变点出现在坡度15°，说明坡度小于15°以下的年最大雪深空间差异小，相对而言，坡度大于15°区域的年最大雪深空间变异性较大。

3 雪深与高程、坡度的回归分析

通过对研究区不同高程带与分布坡度均值和雪深均值的相关分析得知，雪深均值与坡度的相关性较小，未通过0.05显著性检验，说明坡度并非影响雪深分布的限制因子;雪深均值与高程的关系密切，相关系数达0.767，通过了0.001显著性检验。在高程固定的条件下，雪深均值与坡度的偏相关系数为－0.333，表明高原雪深分布受到高程和坡度的双重影响，高程是雪深分布的主要影响因子。

为更好地揭示高程和坡度因子对积雪深度的影响，在相关分析基础上，对积雪深度与高程、坡度进行多元回归分析，标准化回归方程为

式中:D为雪深;E为高程;S为坡度。该回归方程的复相关系数达0.796，通过了0.001的显著性检验。可以看出，高程对积雪深度的影响有正效应，坡度对积雪深度的影响表现为负效应，高程是影响积雪深度分布的主要地形驱动因子。综上所述，不同高程带坡度的分布会造成雪深空间差异性的变化。

不同高程带坡度标准差和雪深标准差的分布情况如图8所示。

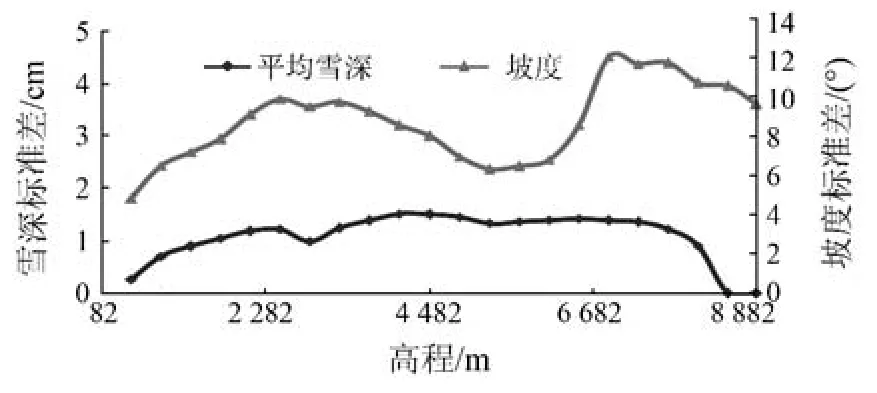
图8 坡度标准差、雪深标准差与高程分布的关系Fig.8 Relationship between elevation distribution and slope standard deviation，snow depth standard deviation

从图8可以看出，在高程82～3 282 m区间，平均雪深标准差和坡度标准差变化趋势比较一致，相关系数达0.937，达到了0.001显著性水平，说明坡度的空间差异对平均雪深空间变异的影响具有明显正效应;在高程3 282 m以上，坡度标准差呈“下降—上升—下降”大幅波动态势，而平均雪深标准差变化平稳，二者呈负相关，相关系数为－0.315，说明坡度的空间差异对平均雪深空间变异的影响较小。

4 结论与讨论

1)青藏高原雪深分布存在2个高值区:①东南高值区，集中在唐古拉山、念青唐古拉山东段山区带和巴颜喀拉山，年均雪深最大值可达10 cm;②西部和西南部高值区，位于喀喇昆仑山山脉、喜马拉雅山西段，多年平均积雪深度的范围在3～7 cm之间。

2)月最大雪深受高程影响显著，并伴随有明显的陡坎效应;在5—9月平均雪深主要受高程影响，在其他月份则受气温和高程共同影响;高原雪深分布受高程和坡度的双重影响，高程是雪深分布的主要影响因子，但在高程82～3 282 m区间，坡度的空间差异对平均雪深空间变异的影响具有明显正效应。

3)年最大雪深的均值随高程增加呈不显著上升趋势，其随高程的突变点在882 m处，年最大雪深的空间差异性随高程增加而呈显著下降趋势，高程7 282 m以下区域年最大雪深空间差异性大;年最大雪深的均值随坡度增加呈不显著上升趋势，年最大雪深的空间差异性随坡度增加而呈显著上升趋势，年最大雪深空间差异性的突变点出现在坡度15°处，坡度在15°以下年最大雪深空间差异小。

4)从10月至翌年5月，平均雪深在高程82～2 482 m和6 082～7 682m区间，受坡度影响较高程2 482～6 082 m大，同一高程上雪深变化明显。回归分析表明，高原雪深分布受到高程和坡度的双重影响，高程是雪深分布的主要影响因子，在高程82～3 282m区间，坡度的空间差异对平均雪深空间差异性的影响具有明显正效应。

5)地形因素中坡向对雪深的分布有很大影响，正常情况下，阳坡的雪比阴坡融化得快，因此很多地区同一高程，阴面有雪，但阳面没有雪，所以还需更高空间分辨率的DEM数据与卫星积雪数据进行局地分析，进而得出更精确的结论。不同高程带上的气候、坡度、坡向、地表温度及地表覆盖等有很大差异，因此研究不同高程带上积雪的时空动态变化及影响因素，需综合应用地面台站观测资料、多源遥感积雪数据及各类数值模拟产品，以便提高卫星遥感积雪数据反演雪深的精度。

［1］ 徐兴奎.1970—2000年中国降雪量变化和区域性分布特征［J］.冰川冻土，2011，33(3):497－503.Xu X K.Spatiotemporal variation and regional distribution characteristics of snowfall in China from 1970 to 2000［J］.Journal of Glaciology and Geocryology，2011，33(3):497－503.

［2］ 纪 鹏，郭华东，张 露.近20年西昆仑地区冰川动态变化遥感研究［J］.国土资源遥感，2013，25(1):93－98.doi:10.6046/gtzyyg.2013.01.17.Ji P，Guo H D，Zhang L.Remote sensing study of glacier dynamic change in West Kunlun Mountains in the past20 years［J］.Remote Sensing for Land and Resources，2013，25(1):93－98.doi:10.6046/gtzyyg.2013.01.17.

［3］ 车 涛，李 新，高 峰.青藏高原积雪深度和雪水当量的被动微波遥感反演［J］.冰川冻土，2004，26(3):363－368.Che T，Li X，Gao F.Estimation of snow water equivalent in the Tibetan Plateau using passivemicrowave remote sensing data(SSM/I)［J］.Journal of Glaciology and Geocryology，2004，26(3):363－368.

［4］ 张佳华，吴 杨，姚凤梅.卫星遥感藏北积雪分布及影响因子分析［J］.地球物理学报，2008，51(4):1013－1021.Zhang JH，Wu Y，Yao FM.Study on the snow distribution and influencing factors in Northern Tibet based on remote sensing information［J］.Chinese Journal of Geophysics，2008，51(4):1013－1021.

［5］ Che T，Li X，Jin R，et al.Snow depth derived from passivemicrowave remote－sensing data in China［J］.Annals of Glaciology，2008，49(1):145－154.

［6］ 柏延臣，冯学智，李 新，等.基于被动微波遥感的青藏高原雪深反演及其结果评价［J］.遥感学报，2001，5(3):161－165.Bo Y C，Feng X Z，Li X，etal.The retrieval of snow depth in Qinghai_Xizang(Tibet)Plateau from passivemicrowave remote sensing data and its results assessment［J］.Journal of Remote Sensing，2001，5(3):161－165.

［7］ 车 涛，李 新.利用被动微波遥感数据反演我国积雪深度及其精度评价［J］.遥感技术与应用，2004，19(5):301－306.Che T，Li X.Retrieval of snow depth in China by passive microwave remote sensing data and its accuracy assessment［J］.Remote Sensing Technology and Application，2004，19(5):301－306.

［8］ 车 涛.积雪被动微波遥感反演与积雪数据同化方法研究［D］.兰州:中国科学院寒区旱区环境与工程研究所，2006.Che T.Study on Passive Microwave Remote Sensing of Snow and Snow Data Assimilation Method［D］.Lanzhou:Cold and Arid Regions Environmental and Engineering Research Institute，2006.

［9］ 白淑英，史建桥，沈渭寿，等.近30年西藏雪深时空变化及其对气候变化的响应［J］.国土资源遥感，2014，26(1):144－151.doi:10.6046/gtzyyg.2014.01.25.Bai SY，Shi JQ，Shen W S，et al.Spatial－temporal variation of snow depth in Tibet and its response to climatic change in the past 30 years［J］.Remote Sensing for Land and Resources，2014，26(1):144－151.doi:10.6046/gtzyyg.2014.01.25.

［10］ 韦志刚，黄荣辉，陈 文.青藏高原冬春积雪年际振荡成因分析［J］.冰川冻土，2005，27(4):491－497.Wei ZG，Huang R H，Chen W.The causes of the interannual variation ofsnow cover over the Tibetan Plateau［J］.JournalofGlaciology and Geocryology，2005，27(4):491－497.

［11］ 杨 倩，陈圣波，路 鹏，等.2000—2010年吉林省积雪时空变化特征及其与气候的关系［J］.遥感技术与应用，2012，27(3):413－419.Yang Q，Chen SB，Lu P，et al.Spatio－temporal variation of snow cover in Jilin province and its relationships to climate change in recent10 years［J］.Remote Sensing Technology and Application，2012，27(3):413－419.

［12］ 孙鸿烈.不断攀登探索世界屋脊奥秘［J］.中国西藏，1998(6):46－48.Sun H L.Climbing up and exploringmysteries concerning the roof ofworld［J］.China’s Tibet，1998(6):46－48.

［13］ 魏凤英.现代气候统计诊断与预测技术［M］.北京:气象出版社，2007.Wei F Y.Modern Climatic Statistical Diagnosis and Prediction Technology［M］.Beijing:Meteorological Press，2007.

［14］ 徐宗学，米艳娇，李占玲，等.和田河流域气温与降水量长期变化趋势及其持续性分析［J］.资源科学，2008，30(12):1833－1838.Xu ZX，Mi Y J，Li Z L，etal.Long－term trendsand sustainability analysis of air temperature and prediction in the Hotan river basin［J］.Resources Science，2008，30(12):1833－1838.

［15］ 白淑英，史建桥，相 栋，等.近50年青海降水时空格局变化［J］.干旱区资源与环境，2013，27(6):148－153.Bai SY，Shi JQ，Xiang D，et al.Spatiotemporal pattern change of precipitation in Qinghai in the last 50 years［J］.Journal of Arid Land Resources and Environment，2013，27(6):148－153.

［16］ 康淑媛，张 勃，柳景峰，等.基于Mann－Kendall法的张掖市降水量时空分布规律分析［J］.资源科学，2009，31(3):501－508.Kang S Y，Zhang B，Liu JF，et al.Analysis of the spatiotemporal distribution of precipitation in Zhangye City using Mann－Kendall method［J］.Resources Science，2009，31(3):501－508.

［17］ 王叶堂，何 勇，侯书贵.2000—2005年青藏高原积雪时空变化分析［J］.冰川冻土，2007，29(6):855－861.Wang Y T，He Y，Hou SG.Analysisof the temporal and spatial variations of snow cover over the Tibetan Plateau based on MODIS［J］.Journal of Glaciology and Geocryology，2007，29(6):855－861.