铅酸蓄电池动态模型参数辨识及仿真验证
李匡成,刘 政
(装甲兵工程学院控制工程系,北京 100072)
0 引言
铅酸蓄电池主要的参数有荷电状态 SOC、静止电动势Em、欧姆内阻R0、极化电阻R1等,而这些参数受大量因素的影响,所以需要建立铅酸蓄电池等效电路模型,并对其中的参数进行参数辨识,以实现对蓄电池参数的准确估计,最后通过仿真验证参数辨识的准确性。
1 等效电路模型的建立
现行的蓄电池等效电路可以很好地描述蓄电池在充放电状态的特性,为了更好地模拟铅酸蓄电池充放电状态下的不同参数,对现行的模型进行了改进,如图1所示[1]。

图1 改进的蓄电池等效电路模型
该模型为动态模型,考虑电池充放电时元件值随荷电状态和温度而变化。模型包含充电和放电两种工作状态。其中,Em为理想电压源,表示电池的开路电压,与蓄电池的荷电状态、温度有关;电流充电时为正,放电时为负,R0,c和R0,d分别表示在充电和放电两种状态下的欧姆电阻大小,与荷电状态和温度有关[2]。
2 铅酸蓄电池模型参数辨识
2.1 参数辨识流程图
本节主要在建立铅酸蓄电池等效电路模型的基础上,以 7-HKA-182 型铅酸蓄电池为研究对象,设计实验平台,对该型号的铅酸蓄电池进行充放电实验,采集实验数据,采用实验法对该型号铅酸蓄电池进行充放电状态下的参数辨识,最后,对所辨识的参数进行仿真验证,验证参数辨识的准确性。图2给出了铅酸蓄电池等效模型电路参数辨识流程框图。

2.2 参数辨识结果
2.2.1 静止电动势参数辨识
2.2.1.1 线性最小二乘法
在科学技术及生产实践中,常常需要寻找某些参量直接的定量关系式,即由已知数据确定经验或半经验的数学模型,以便分析预测。当这些参量之间的数学关系式不能从理论上导出或者理论公式过于复杂时,常用的方法是将观测到的离散数据标记在平面图上,这只是对一个变量的情况而言,将描成一条光滑的曲线(也包括直线或对数坐标下的直线等)。本文参数辨识采用曲线拟合的最小二乘法,对于多变量离散函数 (yj,xij) (i=1, 2,…,p;j=1,2,…,m) 常常利用线性最小二乘法拟合为线性的多元函数,即:

其中,Y=y为因变量,X=[x1,x2, …,xp]T为自变量,B=[b1,b2, …,bn]T为待定系数,F=[f1,f2, …,fn]T为X的函数关系式,写作标量形式如下:

可以看出,待定系数B处于与y呈线性关系的位置,因此称上式为线性多元函数,对这类函数的最小二乘法拟合称作线性最小二乘法[3]。
2.2.1.2 静止电动势Em的参数辨识
铅酸蓄电池的静止电动势Em与荷电状态呈线性关系。传统铅酸蓄电池静止电动势的模型采用了经验公式(3),且该经验公式包含了温度对静止电动势的影响,经验证,该关系模型准确性较高,便于实际应用,由于经验公式的系数随蓄电池的型号不同而改变。
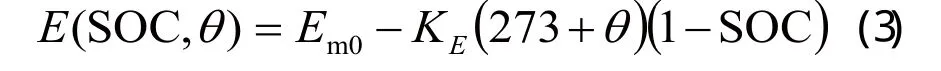
式中:Em0为开路电压;KE是每升高一个温度引起的电压变化;θ是温度,单位 ℃。
由于实验条件限制及为了精简参数辨识工作,本实验只考虑了常温下不同荷电状态的参数辨识,根据实验数据,采用线性最小二乘法可以辨识实验用蓄电池的静止电动势模型参数。利用表1实验数据进行拟合得到:

将拟合曲线和实验图相比较,得到图3。
2.2.2 欧姆内阻参数辨识
铅酸蓄电池在充电的初始时刻,其内阻主要为欧姆内阻,可以通过测得不同时刻的电压和电流变化率,来知道其内阻大小,但由于测量时间间隔一般为 0.5~l ms,增大其测量难度。当以方波电流充电时,由:

表1 25 A 和 12 A 两阶段充电实验下不同 SOC 时铅酸蓄电池静止电动势测量值

图3 Em-SOC 拟合值与实验值的关系图

即可算出铅酸蓄电池的欧姆内阻,ΔU为该时刻的电压变化量。本实验以 25 A 和 12 A 两阶段恒流充电为例,得到不同 SOC 下的欧姆内阻测量值,如表2所示。将数据拟合可以得到二次拟合曲线:
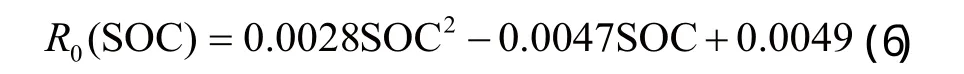
将拟合曲线和实验曲线相比较,得到图4。

表2 25 A 和 12 A 两阶段充电实验下不同 SOC 时铅酸蓄电池欧姆内阻测量值

图4 R0-SOC 拟合值与实验值的关系图
3 仿真验证
模型准确性验证的实验值通过两阶段充电实验获取。以 7-HKA-182 型铅酸蓄电池为实验蓄电池,额定容量为 182 Ah。两阶段充电中,第一阶段25 A,持续时间 8 h,之后改为 12 A 继续充电。仿真实验是在 Matlab 7.8 环境下获取的。仿真时间设置为 4680 s,采样点间隔为 1 min,电流误差小于5%,充电效率设置为 0.75,初始荷电状态 SOC 设置为 0,初始端电压UL为 14.35 V,图5所示为铅酸蓄电池参数的仿真值与实验值的比较曲线。
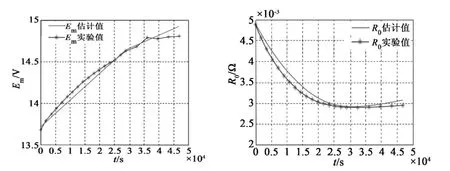
图5 参数仿真值与实验值的关系曲线图
4 结论
从仿真结果与实验结果可以看出,蓄电池等效电路模型具有较高的准确性,但是还存在一定的误差,这些误差主要是由实验测量和等效电路模型简化引起的。铅酸蓄电池的端电压的实验测量值受实验设备和实验条件的影响产生了测量误差,而模型中的端电压则是由极化电势、静止电动势和欧姆内阻电压共同组成的,由于模型的简化性,使得仿真值与实验值存在一定的误差。
[1] 王志国, 高玉峰, 杨万里.铅酸蓄电池等效电路模型研究[J].装甲兵工程学院学报, 2003, 17(1):78–81.
[2] 马巍.电动汽车铅酸蓄电池特性建模与荷电状态估计[D].西安: 长安大学, 2009.
[3] 林瑞霖, 郭辉.最小二乘支持向量机在蓄电池剩余容量建模中的应用研究[J].海军工程大学学报, 2010, 22(5): 52–55.

