基于稀疏自动编码器的飞参数据异常检测
基于稀疏自动编码器的飞参数据异常检测
杜辰飞,曲建岭,孙文柱,高峰
(海军航空工程学院青岛校区,山东 青岛 266041)
摘要:为了改善人工判读飞参数据效率低且易出现误判和漏判的不良状况,本文提出一种基于稀疏自动编码器(Sparse auto-encoder,SAE)的飞参数据异常检测方法。首先构建了SAE的基本框架,然后以滑动窗口的形式生成训练样本。其次,用正常样本并结合BP算法对整个网络模型进行训练和优化以得到相应的正常样本重构误差分布阈值。最后,根据测试样本的重构误差对飞参数据中的典型异常进行检测。实验证明,该方法可在样本不平衡的情况下,仅利用正常样本构建参数空间,并得到正常样本重构误差分布门限,准确检测出飞参数据中的异常,实现飞参数据机器判读。
关键词:飞参数据;异常检测;稀疏自动编码器;反向传播算法;重构误差
doi:10.11823/j.issn.1674-5795.2015.02.03
中图分类号:V328.3;TP181
文章编号:1674-5795(2015)02-0011-04
收稿日期:2015-01-23;修回日期:2015-03-06
作者简介:杜辰飞(1988-),男,硕士研究生,主要研究方向为航空仪表;曲建岭(1968-),男,教授,博士,主要研究方向为航空仪表、飞参数据应用、人工智能、模式识别等。
Flight Data Abnormity Detection Method Based on Sparse Auto-encoder
DU Chenfei,QU Jianling,SUN Wenzhu,GAO Feng
(Naval Aeronautical Engineering Institute Qingdao Branch,Qingdao 266041,China)
Abstract:To improve the adverse conditions of flight data manual interpretation such as low efficiency and inevitable errors or omissions,this paper presents a method based on sparse auto-encoder(SAE)for flight data abnormity detection.Firstly,we make the basic framework for SAE.Secondly we generate the training samples in the form of a sliding window.Thirdly,we use normal samples and BP algorithm to fulfill training and optimization of the entire network so as to get reconstruction error distribution threshold of normal samples.Finally,according to the reconstruction error of test samples we detect typical abnormity in flight data.Experiments show that this computer-based flight data interpretation method can get reconstruction error threshold distribution of the normal samples in the case of sample imbalance and detect abnormity of flight data accurately.
Key words:flight data;abnormity detection;sparse auto-encoder;back-propagation algorithm;reconstruction error

0引言
高强度的飞参判读工作使飞参判读员长期处于疲劳状态,增加了飞参判读误判、漏判的概率,而不断完善的飞机安全监控和视情维护体制却对飞参判读的效率和准确率提出了更高的要求。深度学习技术的兴起和异常检测方法的日趋完善为解决上述问题奠定了理论基础。深度学习神经网络是一种利用经过无监督逐层贪心预训练和精雕的多隐含层非线性网络结构从无类标数据样本中提取高维复杂输入数据的分层特征,进而得到数据集压缩表示的机器学习算法[1],其最大的优势在于它将模式识别和特征分类器结合到一个框架中,不但能发掘同类数据的内在线性或非线性关系,而且能明确不同类别数据间的界限,提高了无类标数据样本的利用率,克服了传统浅层神经网络梯度稀释、训练时间长和易陷入局部最小等缺陷[2-4]。稀疏自动编码器是一种典型的深度结构,能充分体现深度理论的优势,弥补传统浅层结构的不足,在样本数量不平衡的情况下,有效利用正常样本得到重构误差函数的分布规律,确定分类边界。因此本文提出基于SAE的飞参数据异常检测方法,辅助机器判读,减少误判和漏判,提高飞参判读的效率和准确率。
1SAE方法原理
为解决浅层神经网络受到梯度稀释的影响不能精确拟合高维复杂函数且容易陷入局部最小等问题,2006年Hinton提出深度学习的概念,将限制性波尔兹曼机用于构建深度置信网络,并用无监督逐层贪心训练算法对DBN进行预训练,取得了良好的效果,开启了神经网络研究的新纪元[5]。2007年Benjio经过对深度结构的细致研究,提出稀疏自动编码器的概念,利用KL散度惩罚隐含层节点的激活值,将其约束在非激活状态值附近,因而隐含层节点数量很大时,该结构依然能提取输入数据的结构性特征,提取高维数据变量的稀疏解释性因子,有效保留原始输入的非0特征,提高了表示学习算法的鲁棒性,增强了数据的线性可分性,使分类边界更加清晰,并且能有效控制变量规模,在一定程度上改变数据内部结构,丰富了原始数据包含信息,使得信息表述的全面性和准确率得到显著的提高[6],因此SAE被广泛用于图像分类、图像还原和图像去噪等领域[7-9]。2012年马云龙将并列SAE用于异常值检测取得了良好的效果[10],2013年邓俊利用SAE实现了语义情感辨识[11]。
SAE的基本结构如图1所示,输入层接收d维输入向量x∈[0,1]d,然后将其映射到隐含表示y∈[0,1]d′,该映射可表示为
y=fθ(x)=s(Wx+b)
(1)
式中:θ={W,b}为网络参数;s为sigmoid函数;W为d′×d维的权值矩阵;b为偏置向量。

图1 稀疏自动编码器
隐含层表达y通过逆映射得到重构向量z∈[0,1]d,逆映射为
z=gθ′(y)=s(W′y+b′)
(2)
式中:θ′={W′,b′};W′为d×d′维的权值矩阵;b′为偏置向量;且有W′=WT,因而SAE具有关联的权值。
样本xi首先映射到yi,然后通过逆映射得到重构zi,{θ,θ′}用最小均方误差函数来优化网络参数,其表达式为
(3)
式中:n为样本数量;L为平方误差,即

(4)
SAE的核心是对原型自动编码器的代价函数加入约束条件,使大部分隐含层节点处于“抑制”状态,将隐含层节点输出值限定在0附近[12],SAE的代价函数表达式为

(5)
式中:ρ为隐含层节点的激活值;ρj为隐含层节点的平均激活值;β为常数,代表稀疏惩罚项的比重。
惩罚项的实质是Kullback-Leibler(KL)散度[13],表示的是分别具有平均值ρ和ρj且服从贝努利分布的两个随机变量之间的差距,一般形式为

(6)
为了对SAE进行精雕,本文采用BP算法对SAE进行整体性调整[13-15],基本方法如下:

(7)


(8)
(9)
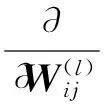
1)根据初始化的权值矩阵和偏置进行前馈传导计算,利用前向传导公式,得到L2,L3,…,Lnl的激活值。
2)对于第Lnl层(输出层)的每个输出单元i,我们根据以下公式计算残差


(10)
3)对l=nl-1,nl-2,nl-3,…,2的各个层,第l层的第i个节点的残差计算方法如下
(11)


(12)
根据递推过程我们将nl-1与nl的关系替换为l与l+1的关系,因而可以得到
(13)
因此,SAE梯度可表示为
(14)
4)计算SAE偏导数

(15)

(16)
2飞参数据异常检测
飞参数据中的正常样本远多于异常样本,并且飞参数据异常的种类有很多,由此带来的样本不平衡问题严重影响了传统神经网络的分类效果(如图2、3所示),同时,浅层结构不能拟合高维复杂函数使分类器精度受到一定程度的影响[16-18]。为了克服上述缺陷,本文从某型飞机300个架次的飞行数据中提取正常样本用于训练SAE以得到正常数据的重构误差分布阈值(如图4所示),最后用完成训练的SAE检测带有异常的飞行数据。若该数据存在异常,那么其对应时刻的代价函数将超出阈值;因此,若超出阈值,则可判定该时刻的飞行数据出现异常。检测结果用0,1表示,0表示该时刻飞行数据正常,1表示该时刻飞行数据异常。

图2 样本平衡分类效果

图3 样本不平衡分类效果
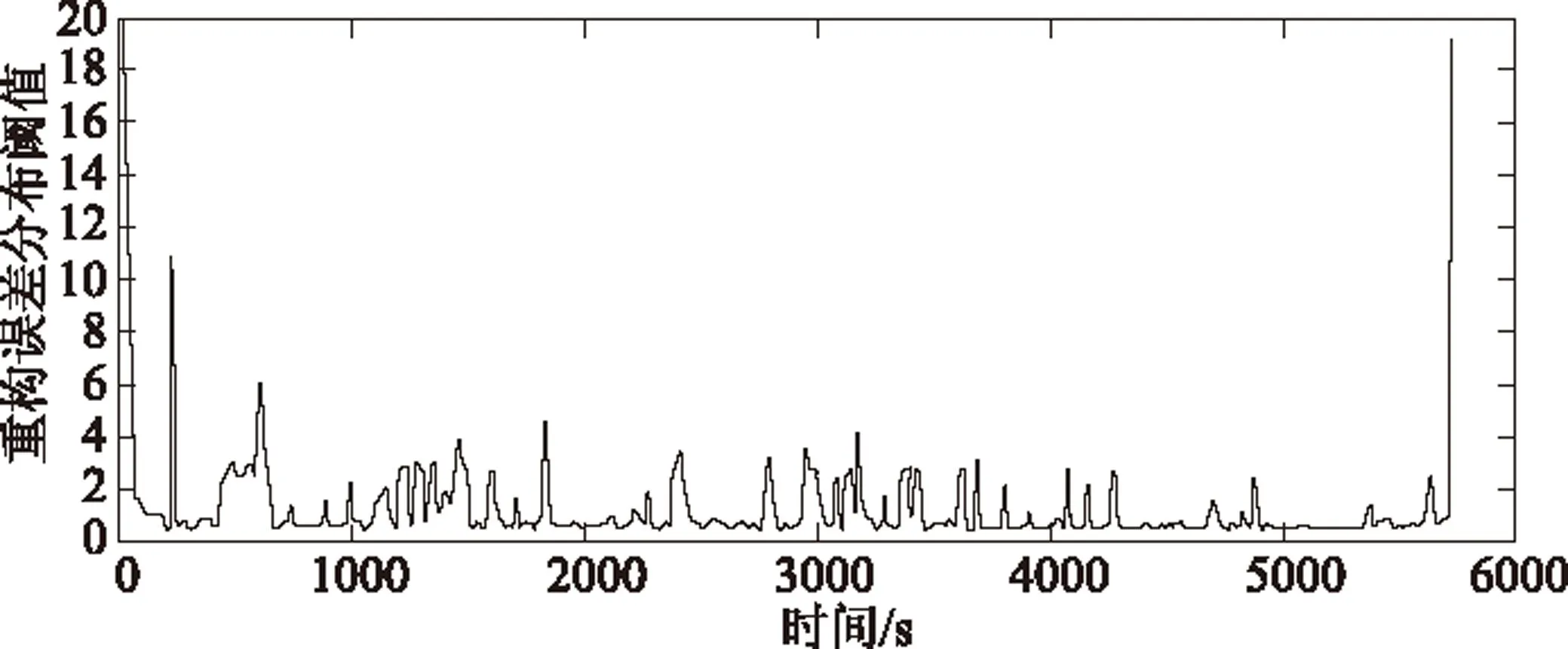
图4 重构误差分布阈值
2.1飞参样本提取方法
飞参训练样本可由一个或几个参数构成,便于SAE捕捉到正常样本代价函数特征,确定分类边界,提升训练的效率和检测的准确率。
根据发生异常的参数种类,本文选取左发排气温度(T4_L)、右发排气温度(T4_R)、左发高压转子转速(N2_L)、右发高压转子转速(N2_R)、左发低压转子转速(N1_L)、右发低压转子转速(N1_R)、左发滑油压力(PH_L)、右发滑油压力(PH_R)、左发滑油温度(TH_L)、右发滑油温度(TH_R)共10个参数构建一个宽度为12 s,移动步长为1 s的滑动窗口作为一个训练样本。
2.2飞参数据异常检测实例
1)野值检测
野值是一种与先验知识不符的数据,一般由线路接触不良或瞬间强干扰产生,是数字式记录设备中不可避免的电气特性,一般表现为采样点严重偏离正常状态,曲线中含有尖峰或毛刺。如图5所示,某架次飞行数据发动机滑油压力中含有野值,相应的检测效果如图6所示。

图5 含有野值的滑油压力

图6 滑油压力野值检测
2)发动机喘振检测
喘振是由于气流在涡轮发动机压气机的叶片通道内严重分离而造成的压气机不稳定,从而使涡轮发动机的工作状态严重地偏离了设计工作状态的故障。发生喘振时,可以观察到发动机工作不连续,高压转子转速迅速下降,排气温度急剧升高。如图7所示,2203~2209 s右发发生喘振,相应的检测效果如图8所示。

图7 右发喘振

图8 喘振检测
2.3检测效果比较
在样本不平衡的情况下,本文所用方法的检测效果明显优于基于浅层神经网络的方法和完全依靠熟练人工判读的效果。实验与统计数据如表1所示(实验中,检测飞参数据异常327个)。
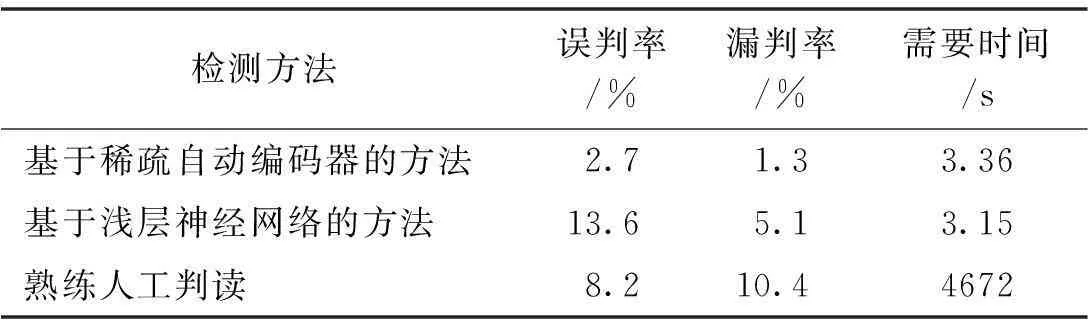
表1 检测效果比较
3结论
传统的异常检测方法需要大量的先验知识,但是飞参数据中的异常样本极少,已经发生的异常仅是个
例,因而传统检测方法无法提取飞参数据异常的特征,对新生种类异常的检测效果较差。同时,浅层结构不能拟合高维复杂函数,非凸优化能力较差,梯度稀释使模型易陷入局部最小,分类效果较差。而以SAE为理论基础的异常检测方法的最大优势就是可以在遇到未知种类的异常时,通过学习正常飞行参数的代价函数模式来识别异常数据。理论上,如果训练样本完备,基于SAE的方法可以发现所有异常模式并确定异常发生的时刻,检测准确率接近100%,因此,将SAE用于飞行数据异常检测是实现飞行数据机器判读的有效途径。
参考文献
[1] HINTON G,OSINDERO S.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554.
[2] ERHAN D,BENGIO Y,COUVILLE A.Why does unsupervised pre-training help deep learning[J].Journal of Machine Learning Research,2010,11(3):625-660.
[3] POON H,DOMINGOS P.Sum-product networks:a new deep architecture[C]//Proc of IEEE International Conference on Computer Vision.Barcelona:IEEE,2011:689-690.
[4] ZINKEVICH M,SMOLA A,WEIMER M,et al.Parallelized stochastic gradient descent[J]Advances in Neural Information Processing Systems.2010(23):2595-2603.
[5] BENGIO Y.Learning deep architectures for AI[J].Foundations and Trends in Machine Learning,2009,2(1):1-127.
[6] BENGIO Y,LAMBLIN P,POPOVICI D.Greedy layerwise training of deep networks in Advances[C]//Proc of the 20thInternational Conference on Neural Information Processing Systems.Cambridge:MIT Press,2007:153-159.
[7] 孙志军,薛磊,许阳明.深度学习研究综述[J].计算机应用研究,2012,29(8):2805-2810.
[8] GLOROT X,BORDES A,BENGIO Y.Deep Sparse Rectifier Neural Networks[C]//Proc of the 14thInternational Conference on Artificial Intelligence and Statistics.Fort Lauderdale:IEEE,2011:315-323.
[9] BENGIO Y,DELALLEAU O.On the expressive power of deep architectures[C]//Proc of the 14thInternational Conference on Discovery Science.Berlin:Springer-Verlag,2011:18-36.
[10] YUNLONG MA,PENG ZHANG,YANAN CAO.Parallel Auto-encoder for Efficient Outlier Detection[C]//Proc of IEEE International Conference on Big Data.Silicon Valley:IEEE,2013:15-17.
[11] MUHAMMAD G,BASTIAAN K W,MENGJIE Zhang.Sparse Representations in Deep Learning for Noise-Robust Digit Classification[C]//Proc of the 28thInternational Conference on Image and Vision Computing.Wellington:IEEE,2013:340-345.
[12] CHARALAMPOUS K,KOSTAVELIS I,AMANATIADIS A. Sparse deep-learning algorithm for recognition and categorization[J].Electronics Letters,2012,48(20):55-56.
[13] YUXI LUO,YI WAN.A Novel Efficient Method for Training Sparse Auto-Encoders[C]//Proc of the 6thInternational Congress on Image and Signal Processing.Hangzhou:IEEE,2013:1019-1023.
[14] XIAO JUAN JIANG,YINGHUA ZHANG,WENSHENG ZHANG.A Novel Sparse Auto-Encoder for Deep Unsupervised Learning[C]//Proc of the 6thInternational Conference on Advanced Computational Intelligence.Hangzhou:IEEE,2013:256-261.
[15] BENJAMIN L,ROMAIN H,CLEMENT C.Learning Deep Neural Networks for High Dimensional Output Problems[C]//Proc of the IEEE International Conference on Machine Learning and Applications.Miami Beach:IEEE,2009:63-68.
[16] WONG W K,MINGMING SUN.Deep Learning Regularized Fisher Mappings[J].IEEE Transactions on Neural Networks,2011,22(10):1668-1675.
[17] BENGIO SAMY,LI DENG,HUGO LAROCHELLE.Guest Editors’ Introduction:Special Section on Learning Deep Architectures [J].IEEE Transactions On Pattern Analysis And Machine Intelligence,2013,35(8):1795-1797.
[18] TELMO AMARAL,LUIS M,LUIS S.Using Different Cost Functions to Train Stacked Auto-encoders[C]//Proc of 12thMexican International Conference on Artificial Intelligence.Mexico City:IEEE,2013:114-120.

